4.1.1 认识三角形 课件

(共44张PPT)
第四章 三角形
4.1.1 认识三角形
1.认识三角形
2.探索三角形全等的条件，体会分类思想。
3.利用尺规作图作全等三角形。
4.利用三角形全等解决实际问题，感受数学与生活的实际联系。
5.进一步积累活动经验，发展推理能力。
同学们,生活中有哪些物体可以近似地看作三角形
走 进 生 活














哪些图形是三角形
⑥
⑦
①
②
④
⑤
⑧
⑨
⑩
③
① ③ ⑦ ⑧ ⑨
是三角形
选 一 选
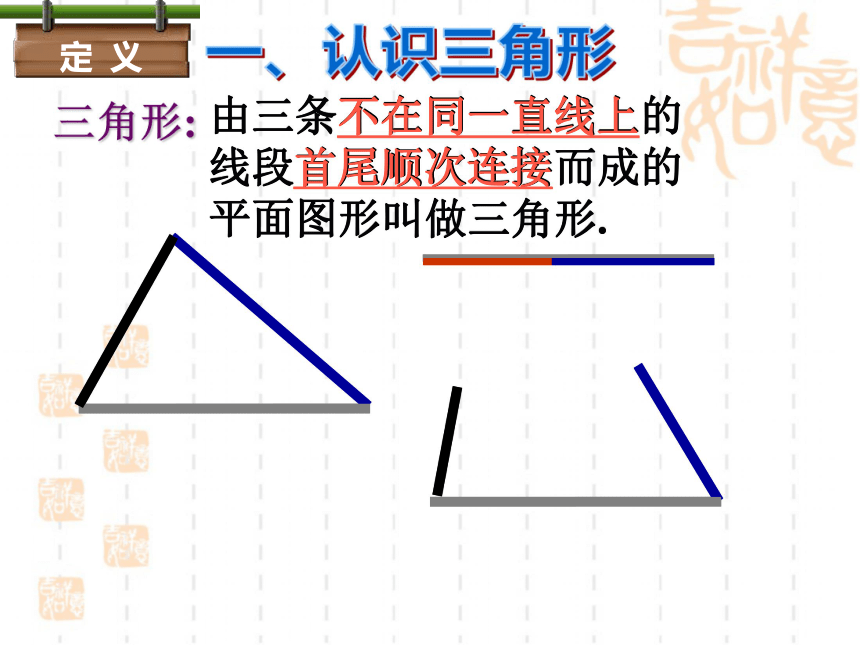
三角形:
由三条不在同一直线上的线段首尾顺次连接而成的平面图形叫做三角形.
不在同一直线上
首尾顺次连接
定 义
叫做三角
形的边
两边的交点叫做三角形的顶点
A
C
B
边
边
边
由三条不在同一直线上的线
段首尾顺次连接而成的平面图形.
三角形:
三 要 素
三 要 素
三角形的三要素：
B
C
c
b
a
Ａ
边：
三角形的三边为AB、BC、AC
顶点A所对的边ＢＣ也可表示为a
顶点Ｂ所对的边ＡＣ也可表示为b
顶点Ｃ所对的边AB也可表示为ｃ
角：
三角形的三个角为∠A，∠B，∠Ｃ
顶点：
三角形的三个顶点Ａ，Ｂ，Ｃ
三 要 素
三 要 素
A
B
C
“三角形”用符号“Δ”表示，如图顶点是A，B，C的三角形记做“ΔABC”，
读做
“三角形ABC”。
（或△ BCA或△ CBA 等）
注意： 顶点字母没有限定次序。
学 一 学
C
B
A
D
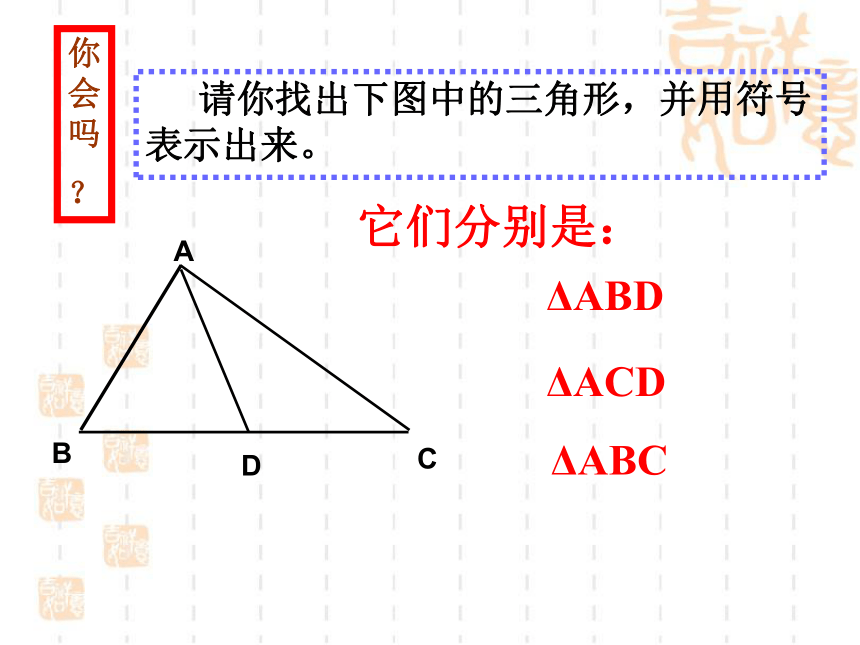
ΔABD
ΔACD
ΔABC
你会吗
？
请你找出下图中的三角形，并用符号表示出来。
它们分别是：
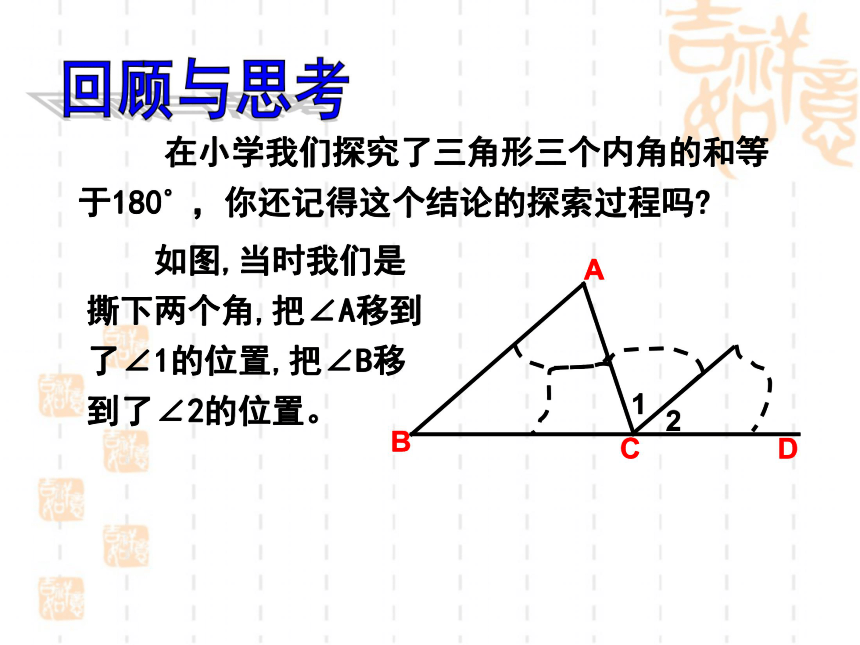
在小学我们探究了三角形三个内角的和等于180 ，你还记得这个结论的探索过程吗
1
A
B
D
2
C
如图,当时我们是撕下两个角,把∠A移到了∠1的位置,把∠B移到了∠2的位置。
如果只撕下一个角,你能用学过的知识拼凑并解释“三角形的三个内角和是180 ”吗？
1
2
3
(1)做一个三角形纸片,它的三个内角分别为∠1,∠2和∠3,如下图.
1
2
3
(2)将∠1撕下,并按上图进行摆放,其中∠1的顶点与∠2的顶点重合,它的一条边与∠2的一条边重合.此时∠1的另一条边b与∠3的一条边a 平行吗 为什么
1
a
b
1
2
3
1
a
b
(3)将∠２与∠３的公共边延长，它与b所夹的角为∠4. ∠3与∠4的大小有什么关系？为什么？
4
由此你能得到什么结论？
三角形的三个内角和等于180度.
你会用几何语言进行证明吗？
证明：
在△ABC的外部，
以CA为一边，
CE为另一边作∠1=∠A，
作BC的延长线CD，
于是CE∥BA
(内错角相等，两直线平行).
∴∠B=∠2
(两直线平行，同位角相等).
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
(等量代换)
）
1
2
C
A
E
）
B
D
还有其他证明方法吗？
证法2：
）
1
2
C
A
E
）
B
D
过C作CE∥BA.
作BC的延长线CD，
于是∠A=∠1
(两直线平行，内错角相等)
∠B=∠2
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
(两直线平行，同位角相等)
(等量代换)
C
A
B
E
F
证法3：
过A作EF∥BC
C
A
B
E
证法4：
过A作AE∥BC
下面的图⑴、图⑵、图⑶中的三角形被遮住的两个内角是什么角？试着说明理由。
将图⑶的结果与图⑴、图⑵的结果进行比较，可以将三角形如何按角分类？
三角形的分类
锐角三角形
三个内角都是锐角
钝角三角形
有一个内角是钝角
直角三角形
有一个内角是直角
直角边
直角边
斜边
1.常用符号“Rt ABC”来表示
直角三角形ABC.
2.直角三角形的两个锐角之间
有什么关系？
直角三角形的两个锐角互余
1.观察下面的三角形，并把它们的标号填入相应图内：
锐角三角形 直角三角形 钝角三角形
③⑤
①④⑥
②⑦
1.一个三角形两个内角的度数分别如下,这个三角形是什么三角形
(1)30度和60度
(2)40度和70度
(3)50度和20度
直角三角形
锐角三角形
钝角三角形
2.在下面的空白处,分别填入“锐角”，“钝角”
或“直角”：
（1）如果三角形的三个内角都相等，那么这个三角形是 三角形；
（2）如果三角形的一个内角等于另外两个 内角之和，那么这个三角形是 三角形；
（3）如果三角形的两个内角都小于40度，那么这个三角形是 三角形.
钝角
锐角
直角
3. △ABC中, ∠A:∠B:∠C=2:3:4,则
∠A= , ∠B= , ∠C= .
4.在△ABC中, ∠A=1/3∠B=1/5∠C,则△ABC
是 三角形.
40°
80°
60°
钝角
5.已知∠ACB=90°，CD⊥AB，垂足为D.
⑴ 图中有几个直角三角形？是哪几个？分别说出它们的直角边和斜边。
⑵ ∠ACD和∠A有什么关系？∠BCD和∠A呢？
C
B
A
D
C
B
A
D
解：直角三角形有三个，分别是：
Rt BDC
Rt ADC
Rt ACB
直角边是AC、BC,斜边AB
直角边是AD、CD,斜边AC
直角边是BD、CD,斜边BC
C
B
A
D
解： ∠ACD和∠A互余
∠BCD和∠A相等
又∵ ∠ACD＋∠A ＋ ∠ADC =180°
证明：在Rt ADC中,∵ CD⊥AB , ∴∠ADC =90°
∴ ∠ACD＋∠A =90°
又∵ ∠ACD＋ ∠BCD= 90°
∴ ∠BCD=∠A
一个三角形中会有两个直角？可能两个内角是钝角或锐角吗？
1. 已知∠A，∠B，∠C是△ABC的三个内角，∠A＝70°，∠C＝30 °， ∠B＝（ ）.
2. 直角三角形一个锐角为70°，另一个锐角等于（ ）.
80 °
20 °
3.在△ABC中，∠A=80°，∠B=∠C，则∠C=（ ）.
4.如果△ABC中，∠A∶∠B∶∠C=2∶3∶5，此三角形按 角分类应为 （ ）.
50 °
直角三角形
有关三角形的角度计算问题，有两种类型：一是直接利用三角形的内角和180°进行计算；二是设某一个角为x（或将某一个角视为未知数），其余的角用x的代数式表示，从而根据题意列出方程（组）求解，这就是“形题数解”。
如图，一艘轮船按箭头所示方向行驶，C处有一灯塔，请你根据图中所标数据求∠ACB的大小，当轮船距离灯塔C最近时，∠ACB是多少度？
30 °
70 °
B
C
A
E
30 °
70 °
B
C
A
E
解：∵∠ABC+∠CBE= 180°
∴ ∠ABC= 180°－∠CBE= 180°－ 70°= 110°
∴在 ABC中， ∠ACB= 180°－ ∠ABC － ∠A
= 180°－ 110° － 30°
= 40°
30 °
90 °
B
C
A
解：当轮船距离灯塔C最近时，则有CB⊥AB
即∠ACB = 90°
∴在 ABC中， ∠ACB= 180°－ ∠ABC － ∠A
= 180°－ 90° － 30°
= 60°
1.三角形三个内角的和等于180 .
2.三角形按角的大小分类：
⑴锐角三角形 ：三个内角都是锐角；
⑵直角三角形 ：有一个内角为直角；
⑶钝角三角形 ：有一个内角为钝角 。
3.直角三角形的两个锐角互余。
请你谈一谈:
通过这节课的学习,你对三角形又多了哪些认识
以三角形为主设计一幅美丽图案并说说你的设计意图，作品我们将公开展览。
2、请你做个“小小设计师”