2018版题型突破高考数学(理)解答题揭秘高端精品专题2.1+中档大题规范练01(三角%2b概率%2b立体几何%2b选讲)(第01期)
文档属性
| 名称 | 2018版题型突破高考数学(理)解答题揭秘高端精品专题2.1+中档大题规范练01(三角%2b概率%2b立体几何%2b选讲)(第01期) |  | |
| 格式 | zip | ||
| 文件大小 | 955.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-18 16:42:09 | ||
图片预览



文档简介
类型
试 题 亮 点
解题方法/思想/素养
三角大题
三角形与外接圆的关系,三角形中的中线问题
正弦定理角化边,余弦定理解三角形边长,面积公式计算面积
概率大题
二项分布的应用,平均数的计算,概率中的决策问题
体现了学生的数学建模能力、数据分析能力和计算能力
立体几何
面面垂直的证明,四棱锥的体积和线面角的求解
利用直观想象证明线线线面的关系,会用空间直角坐标系解决线面角
选讲1(极坐标参数方程)
极直互化,参普互化
非标准形式的直线参数方程的应用
会用直线的参数方程解决距离问题
选讲2(不等式)
解绝对值不等式;绝对值含参的恒成立求参问题
能用零点分段去绝对值解不等式,能将绝对值不等式等价转化求最值解决恒成立问题
1.三角大题
内接于半径为的圆, 分别是的对边,且.
(Ⅰ)求;
(Ⅱ)若是边上的中线, ,求的面积.
【答案】(Ⅰ);(Ⅱ) .
(Ⅱ)以为邻边作平行四边形,在中, .
在中,由余弦定理得.
即: ,解得, .
故.
2.概率大题
某快递公司收取快递费用的标准是:重量不超过的包裹收费10元;重量超过的包裹,除收费10元之外,超过的部分,每超出(不足,按计算)需再收5元.该公司将最近承揽的100件包裹的重量统计如下:
公司对近60天,每天揽件数量统计如下表:
以上数据已做近似处理,并将频率视为概率.
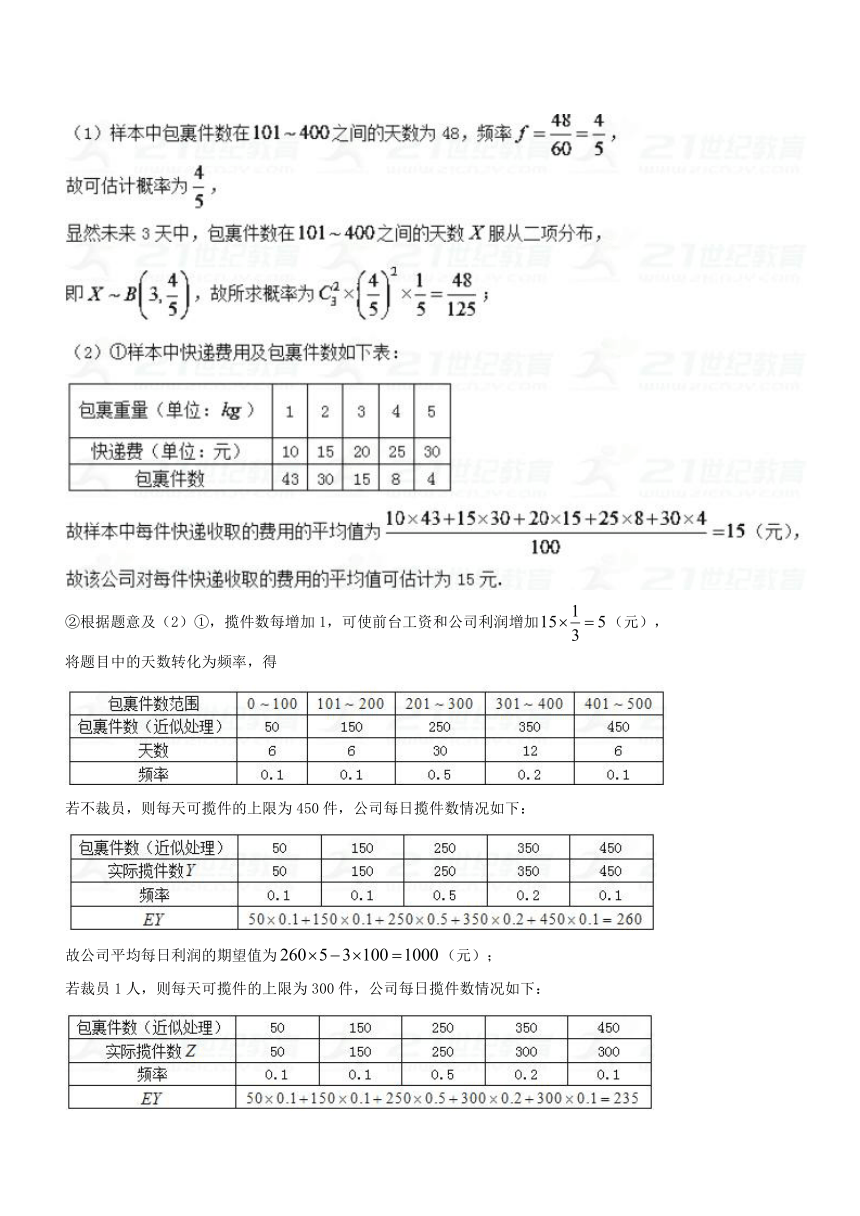
(1)计算该公司未来3天内恰有2天揽件数在之间的概率;
(2)①估计该公司对每件包裹收取的快递费的平均值;
②公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用作其他费用.目前前台有工作人员3人,每人每天揽件不超过150件,工资100元.公司正在考虑是否将前台工作人员裁减1人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
【答案】(1)(2)①15元②公司将前台工作人员裁员1人对提高公司利润不利
【试题解析】
②根据题意及(2)①,揽件数每增加1,可使前台工资和公司利润增加(元),
将题目中的天数转化为频率,得
若不裁员,则每天可揽件的上限为450件,公司每日揽件数情况如下:
故公司平均每日利润的期望值为(元);
若裁员1人,则每天可揽件的上限为300件,公司每日揽件数情况如下:
故公司平均每日利润的期望值为(元)
因,故公司将前台工作人员裁员1人对提高公司利润不利.
3.立体几何
如图,在四棱锥中, ,且.
(Ⅰ)当时,证明:平面平面;
(Ⅱ)当四棱锥的体积为,且二面角为钝角时,求直线与平面所成角的正弦值.
【答案】(1)见解析(2)
试题解析:(Ⅰ)取的中点,连接,
∵为正三角形,∴,
∵,∴,
∵,∴,
∴四边形为矩形,∴,
在中, , , ,∴,∴,
∵,∴平面,
∵平面,∴平面平面.
在平面内过点作垂直于平面的直线为轴,建立空间直角坐标系,
由题意可知, , , , , ,
设平面的一个法向量为,则,得,
令,则,∴,
,设直线与平面所成的角为,
则 .
则直线与平面所成角的正弦值为.
4.选讲1(极坐标参数方程)
在直角坐标系中,以原点为极点,轴的正半轴为极轴建立极坐标系,直线的参数方程为(为参数),曲线的极坐标方程为.
(1)写出直线的普通方程和曲线的直角坐标方程;
(2)若点的坐标为,直线与曲线交于,两点,求的值.
【答案】(1) , (2)8
(2)在(为参数)中,令,
得直线的参数方程的标准形式为(为参数),
代入曲线:,整理得:,
设,所对应参数分别为,,则,,
所以,.
5.选讲2(不等式)
已知函数.
(1)求不等式的解集;
(2)若关于的不等式在上恒成立,求的取值范围.
【答案】(1);(2).
(2)不等式在上恒成立,
在上恒成立,
在上恒成立,
在上恒成立,
由(当且仅当时取等号),
(当且仅当时取等号),
同课章节目录
