2017-2018学年八年级数学下册第20章数据的分析学科素养思想方法(含解析)
文档属性
| 名称 | 2017-2018学年八年级数学下册第20章数据的分析学科素养思想方法(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 305.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-18 19:23:57 | ||
图片预览


文档简介
数据的分析
学科素养·思想方法
一、数形结合思想
【思想解读】化数为形,以形思数,是解决数学问题的关键.数形结合思想不仅为分析问题、解决问题提供了有利条件,而且是培养创新意识、开发智力的重要途径.
【应用链接】数据的分析中涉及图形主要是统计图,统计表,从统计图表中正确获取信息,是解决问题的关键.
【典例1】(2017·福州二模)请根据下列图表信息解答问题:
年份
2011
2012
2013
2014
2015
2016
年增长率
31%
27%
44%
24%
52%
(1)表中空缺的数据为____________.(精确到1%)
(2)求统计表中增长率的平均数及中位数.
【思路点拨】(1)根据折线统计图可以得到2016年的年增长率.
(2)根据平均数与中位数的定义求解.
【自主解答】(1)由题意可得,2016年的年增长率是(13.72-12.60)÷12.60×100%≈9%.
答案:9%
(2)统计表中增长率的平均数为:(31%+27%+44%+24%+52%+9%)÷6≈31%;将它们按从小到大的顺序排列为:9%,24%,27%,31%,44%,52%,
所以中位数是(27%+31%)÷2=29%.
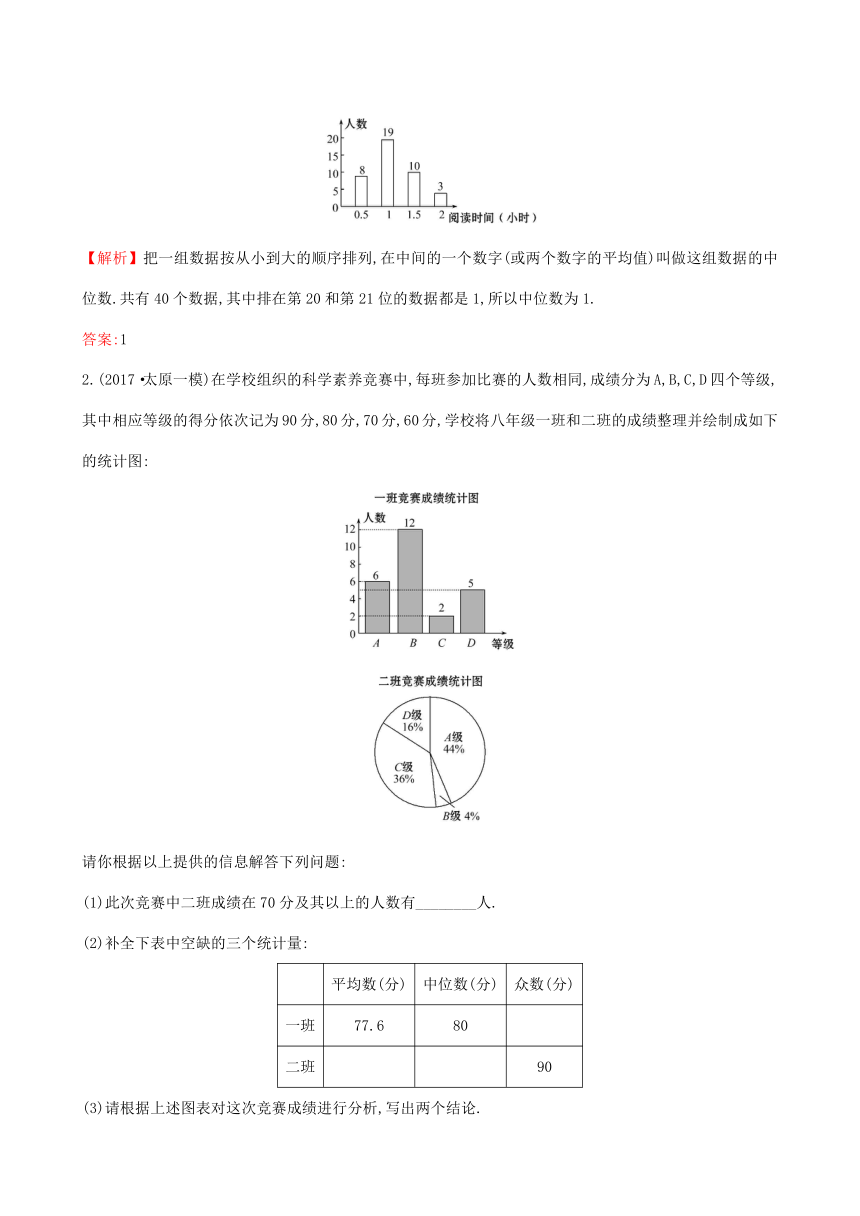
【变式训练】1.为响应“书香成都”建设的号召,在全校形成良好的人文阅读风尚,成都市某中学随机调查了部分学生平均每天的阅读时间,统计结果如图所示,则在本次调查中阅读时间的中位数是________小时.
【解析】把一组数据按从小到大的顺序排列,在中间的一个数字(或两个数字的平均值)叫做这组数据的中位数.共有40个数据,其中排在第20和第21位的数据都是1,所以中位数为1.
答案:1
2.(2017·太原一模)在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在70分及其以上的人数有________人.
(2)补全下表中空缺的三个统计量:
平均数(分)
中位数(分)
众数(分)
一班
77.6
80
二班
90
(3)请根据上述图表对这次竞赛成绩进行分析,写出两个结论.
【解析】(1)一班参赛人数为:6+12+2+5=25(人),
∵两班参赛人数相同,∴二班成绩在70分以上(包括70分)的人数为25×84%=21人.
答案:21
(2)二班平均数:90×44%+80×4%+70×36%+60×16%=77.6(分);中位数:70(分);一班众数:80(分).
填表如下:
平均数(分)
中位数(分)
众数(分)
一班
77.6
80
80
二班
77.6
70
90
(3)①平均数相同的情况下,二班的成绩更好一些.
②请一班的同学加强基础知识训练,争取更好的成绩.
二、样本估计整体思想
【思想解读】根据实际问题的需要合理地选取样本,从样本数据中提取基本的数字特征(如平均数、中位数、众数、方差),并给出合理的解释.用样本的基本数字特征估计总体的基本数字特征.
【应用链接】在数据的分析中,有些问题涉及的统计量特别多,不可能全部分析,这时选取其中的一个样本,用样本的特征估计总体的特征.
【典例2】(2017·丽水模拟)某市为了解高峰时段从总站乘16路车出行的人数,随机抽查了10个班次乘该路车人数,结果如下:
14,23,16,25,23,28,26,27,23,25.
(1)计算这10个班次乘车人数的平均数.
(2)如果16路车在高峰时段从总站共出车60个班次,根据上面的计算结果,估计在高峰时段从总站乘该路车出行的乘客共有多少?
【思路点拨】(1)根据算术平均数的定义列式计算.
(2)用样本中平均每个班次的人数乘以班次.
【自主解答】(1)这10个班次乘车人数的平均数为
×(14+23+16+25+23+28+26+27+23+25)=23.
(2)60×23=1380.
答:估计在高峰时段从总站乘该路车出行的乘客共有1380人.
【变式训练】
1.(2017·东丽区一模)体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
(1)求女生进球数的平均数、中位数.
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
【解析】(1)由条形统计图可得,女生进球数的平均数为:(1×1+2×4+1×3+4×2)÷8=2.5(个);
∵第4,5个数据都是2,则其平均数为2,
∴女生进球数的中位数为2.
(2)样本中优秀率为:,故全校有女生1200人,“优秀”等级的女生为:1200×=450(人),
答:“优秀”等级的女生约为450人.
2.(2017·任城区一模)国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.
根据以上信息,回答下列问题:
(1)A组的人数是________人,并补全条形统计图.
(2)本次调查数据的中位数落在哪个组?
(3)根据统计数据估计该地区25000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有多少人?
【解析】(1)由统计图可得,
A组人数为:60÷24%-60-120-20=50.
补全的条形统计图如图所示.
(2)由补全的条形统计图可得,中位数落在C组.
(3)由题意可得,该地区25000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有:25000×(48%+8%)=14000(人).
三、分类讨论思想
【思想解读】分类讨论思想是指在解决一个问题时,无法用同一种方法去解决,而需要一个标准将问题划分成几个能用不同形式去解决的小问题,将这些小问题一一加以解决,从而使问题得到解决,这就是分类讨论思想.
【应用链接】分类讨论在统计问题中也是常用的一种思想方法.
【典例3】若一组数据2,3,4,5,x的平均数与中位数相同,则实数x的值不可能的是 ( )
A.6 B.3.5 C.2.5 D.1
【思路点拨】因为中位数的值与大小排列顺序有关,而此题中x的大小位置未定,故应该分类讨论x所处的所有位置情况:从小到大(或从大到小)排列在中间、结尾、开始的位置.
【自主解答】选C.(1)将这组数据按从小到大的顺序排列为2,3,4,5,x,处于中间位置的数是4,∴中位数是4,平均数为(2+3+4+5+x)÷5,∴4=(2+3+4+5+x)÷5,解得x=6,符合排列顺序.
(2)将这组数据按从小到大的顺序排列为2,3,4,x,5,中位数是4,此时平均数是(2+3+4+5+x)÷5=4,
解得x=6,不符合排列顺序.
(3)将这组数据按从小到大的顺序排列为2,3,x,4,5,中位数是x,平均数(2+3+4+5+x)÷5=x,
解得x=3.5,符合排列顺序.
(4)将这组数据按从小到大的顺序排列为2,x,3,4,5,中位数是3,平均数(2+3+4+5+x)÷5=3,
解得x=1,不符合排列顺序.
(5)将这组数据按从小到大的顺序排列为x,2,3,4,5,中位数是3,平均数(2+3+4+5+x)÷5=3,
解得x=1,符合排列顺序.∴x的值为6或3.5或1.
【变式训练】已知5个数据:8,8,x,10,10.如果这组数据的某个众数与平均数相等,那么这组数据的中位数是______.
【解析】设众数是8,则由=8,解得:x=4,故中位数是8;设众数是10,则由=10,
解得:x=14,故中位数是10.
答案:8或10
学科素养·思想方法
一、数形结合思想
【思想解读】化数为形,以形思数,是解决数学问题的关键.数形结合思想不仅为分析问题、解决问题提供了有利条件,而且是培养创新意识、开发智力的重要途径.
【应用链接】数据的分析中涉及图形主要是统计图,统计表,从统计图表中正确获取信息,是解决问题的关键.
【典例1】(2017·福州二模)请根据下列图表信息解答问题:
年份
2011
2012
2013
2014
2015
2016
年增长率
31%
27%
44%
24%
52%
(1)表中空缺的数据为____________.(精确到1%)
(2)求统计表中增长率的平均数及中位数.
【思路点拨】(1)根据折线统计图可以得到2016年的年增长率.
(2)根据平均数与中位数的定义求解.
【自主解答】(1)由题意可得,2016年的年增长率是(13.72-12.60)÷12.60×100%≈9%.
答案:9%
(2)统计表中增长率的平均数为:(31%+27%+44%+24%+52%+9%)÷6≈31%;将它们按从小到大的顺序排列为:9%,24%,27%,31%,44%,52%,
所以中位数是(27%+31%)÷2=29%.
【变式训练】1.为响应“书香成都”建设的号召,在全校形成良好的人文阅读风尚,成都市某中学随机调查了部分学生平均每天的阅读时间,统计结果如图所示,则在本次调查中阅读时间的中位数是________小时.
【解析】把一组数据按从小到大的顺序排列,在中间的一个数字(或两个数字的平均值)叫做这组数据的中位数.共有40个数据,其中排在第20和第21位的数据都是1,所以中位数为1.
答案:1
2.(2017·太原一模)在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在70分及其以上的人数有________人.
(2)补全下表中空缺的三个统计量:
平均数(分)
中位数(分)
众数(分)
一班
77.6
80
二班
90
(3)请根据上述图表对这次竞赛成绩进行分析,写出两个结论.
【解析】(1)一班参赛人数为:6+12+2+5=25(人),
∵两班参赛人数相同,∴二班成绩在70分以上(包括70分)的人数为25×84%=21人.
答案:21
(2)二班平均数:90×44%+80×4%+70×36%+60×16%=77.6(分);中位数:70(分);一班众数:80(分).
填表如下:
平均数(分)
中位数(分)
众数(分)
一班
77.6
80
80
二班
77.6
70
90
(3)①平均数相同的情况下,二班的成绩更好一些.
②请一班的同学加强基础知识训练,争取更好的成绩.
二、样本估计整体思想
【思想解读】根据实际问题的需要合理地选取样本,从样本数据中提取基本的数字特征(如平均数、中位数、众数、方差),并给出合理的解释.用样本的基本数字特征估计总体的基本数字特征.
【应用链接】在数据的分析中,有些问题涉及的统计量特别多,不可能全部分析,这时选取其中的一个样本,用样本的特征估计总体的特征.
【典例2】(2017·丽水模拟)某市为了解高峰时段从总站乘16路车出行的人数,随机抽查了10个班次乘该路车人数,结果如下:
14,23,16,25,23,28,26,27,23,25.
(1)计算这10个班次乘车人数的平均数.
(2)如果16路车在高峰时段从总站共出车60个班次,根据上面的计算结果,估计在高峰时段从总站乘该路车出行的乘客共有多少?
【思路点拨】(1)根据算术平均数的定义列式计算.
(2)用样本中平均每个班次的人数乘以班次.
【自主解答】(1)这10个班次乘车人数的平均数为
×(14+23+16+25+23+28+26+27+23+25)=23.
(2)60×23=1380.
答:估计在高峰时段从总站乘该路车出行的乘客共有1380人.
【变式训练】
1.(2017·东丽区一模)体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
(1)求女生进球数的平均数、中位数.
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
【解析】(1)由条形统计图可得,女生进球数的平均数为:(1×1+2×4+1×3+4×2)÷8=2.5(个);
∵第4,5个数据都是2,则其平均数为2,
∴女生进球数的中位数为2.
(2)样本中优秀率为:,故全校有女生1200人,“优秀”等级的女生为:1200×=450(人),
答:“优秀”等级的女生约为450人.
2.(2017·任城区一模)国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.
根据以上信息,回答下列问题:
(1)A组的人数是________人,并补全条形统计图.
(2)本次调查数据的中位数落在哪个组?
(3)根据统计数据估计该地区25000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有多少人?
【解析】(1)由统计图可得,
A组人数为:60÷24%-60-120-20=50.
补全的条形统计图如图所示.
(2)由补全的条形统计图可得,中位数落在C组.
(3)由题意可得,该地区25000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有:25000×(48%+8%)=14000(人).
三、分类讨论思想
【思想解读】分类讨论思想是指在解决一个问题时,无法用同一种方法去解决,而需要一个标准将问题划分成几个能用不同形式去解决的小问题,将这些小问题一一加以解决,从而使问题得到解决,这就是分类讨论思想.
【应用链接】分类讨论在统计问题中也是常用的一种思想方法.
【典例3】若一组数据2,3,4,5,x的平均数与中位数相同,则实数x的值不可能的是 ( )
A.6 B.3.5 C.2.5 D.1
【思路点拨】因为中位数的值与大小排列顺序有关,而此题中x的大小位置未定,故应该分类讨论x所处的所有位置情况:从小到大(或从大到小)排列在中间、结尾、开始的位置.
【自主解答】选C.(1)将这组数据按从小到大的顺序排列为2,3,4,5,x,处于中间位置的数是4,∴中位数是4,平均数为(2+3+4+5+x)÷5,∴4=(2+3+4+5+x)÷5,解得x=6,符合排列顺序.
(2)将这组数据按从小到大的顺序排列为2,3,4,x,5,中位数是4,此时平均数是(2+3+4+5+x)÷5=4,
解得x=6,不符合排列顺序.
(3)将这组数据按从小到大的顺序排列为2,3,x,4,5,中位数是x,平均数(2+3+4+5+x)÷5=x,
解得x=3.5,符合排列顺序.
(4)将这组数据按从小到大的顺序排列为2,x,3,4,5,中位数是3,平均数(2+3+4+5+x)÷5=3,
解得x=1,不符合排列顺序.
(5)将这组数据按从小到大的顺序排列为x,2,3,4,5,中位数是3,平均数(2+3+4+5+x)÷5=3,
解得x=1,符合排列顺序.∴x的值为6或3.5或1.
【变式训练】已知5个数据:8,8,x,10,10.如果这组数据的某个众数与平均数相等,那么这组数据的中位数是______.
【解析】设众数是8,则由=8,解得:x=4,故中位数是8;设众数是10,则由=10,
解得:x=14,故中位数是10.
答案:8或10
