2017-2018学年八年级数学下册第17章勾股定理17.1勾股定理(第1课时)课时提升作业(含解析)
文档属性
| 名称 | 2017-2018学年八年级数学下册第17章勾股定理17.1勾股定理(第1课时)课时提升作业(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 259.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-19 15:53:29 | ||
图片预览


文档简介
勾股定理
(第1课时)
(30分钟 50分)
一、选择题(每小题4分,共12分)
1.(2017·沧州期末)在Rt△ABC中,斜边BC=2,则AB2+AC2+BC2的值为 ( )
A.8 B.4 C.6 D.无法计算
【解析】选A.因为在Rt△ABC中,BC为斜边,
所以AB2+AC2=BC2,
所以AB2+AC2+BC2=2BC2=2×22=8.
2.如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为
( )
A.4S1 B.4S2
C.4S2+S3 D.3S1+4S3
【解析】选A.设等腰直角三角形的直角边为a,正方形边长为c,
则S2=(a+c)(a-c)=a2-c2,
∴S2=S1-S3,
∴S3=2S1-2S2,
∴平行四边形面积=2S1+2S2+S3=2S1+2S2+2S1-2S2=4S1.
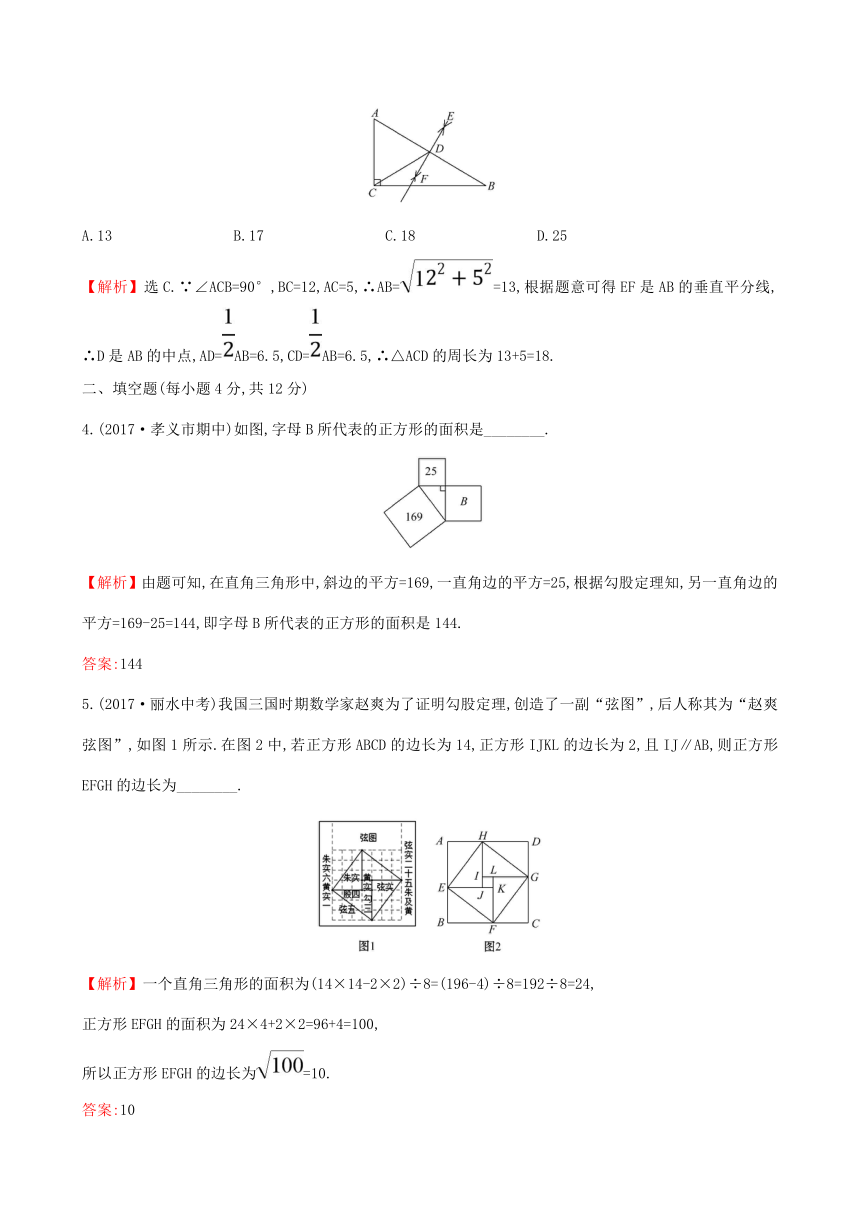
3.(2017·东光县一模)如图,在Rt△ABC中,∠ACB=90°,BC=12,AC=5,分别以点A,B为圆心,大于线段AB长度的一半为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连接CD,则△ACD的周长为 ( )
A.13 B.17 C.18 D.25
【解析】选C.∵∠ACB=90°,BC=12,AC=5,∴AB==13,根据题意可得EF是AB的垂直平分线,∴D是AB的中点,AD=AB=6.5,CD=AB=6.5,∴△ACD的周长为13+5=18.
二、填空题(每小题4分,共12分)
4.(2017·孝义市期中)如图,字母B所代表的正方形的面积是________.
【解析】由题可知,在直角三角形中,斜边的平方=169,一直角边的平方=25,根据勾股定理知,另一直角边的平方=169-25=144,即字母B所代表的正方形的面积是144.
答案:144
5.(2017·丽水中考)我国三国时期数学家赵爽为了证明勾股定理,创造了一副“弦图”,后人称其为“赵爽弦图”,如图1所示.在图2中,若正方形ABCD的边长为14,正方形IJKL的边长为2,且IJ∥AB,则正方形EFGH的边长为________.
【解析】一个直角三角形的面积为(14×14-2×2)÷8=(196-4)÷8=192÷8=24,
正方形EFGH的面积为24×4+2×2=96+4=100,
所以正方形EFGH的边长为=10.
答案:10
6.(2017·路北区期中)在△ABC中,AB=15,AC=13,高AD=12,则△ABC中BC边的长为________.
【解析】(1)如图,在锐角△ABC中,AC=13,AB=15,BC边上高AD=12,
∵在Rt△ACD中AC=13,AD=12,
∴CD2=AC2-AD2=132-122=25,
∴CD=5,
∵在Rt△ABD中,AB=15,AD=12,由勾股定理得
BD2=AB2-AD2=152-122=81,
∴BD=9,
∴BC的长为BD+DC=9+5=14.
(2)在钝角△ABC中,AC=13,AB=15,BC边上高AD=12,
在Rt△ACD中AC=13,AD=12,
由勾股定理得
CD2=AC2-AD2=132-122=25,
∴CD=5,
在Rt△ABD中AB=15,AD=12,由勾股定理得
BD2=AB2-AD2=152-122=81,
∴BD=9,
∴BC的长为BD-DC=9-5=4.
答案:4或14
【变式训练】在Rt△ABC中,∠BAC=90°,AB=AC=2.以AC为一边,在△ABC外部作等腰Rt△ACD,则线段BD的长为________.
【解析】首先要结合题意,画出相应的图形.因为以AC为一边在△ABC外部作等腰Rt△ACD,则AC可以是直角边,也可以是斜边,所以有三种情况:
如图1,BD=4;如图2,BD==2;如图3,∠ACD=90°,
BC=2,CD=,BD==.
答案:4或2或
三、解答题(共26分)
7.(12分)如图,
已知△ABC中,BC=21,AC=10,AB=17,求BC边上的高.
【解析】如图,
过点A作AD⊥BC,垂足为点D.在Rt△ABD与Rt△ACD中,设BD=x,则DC=21-x,由勾股定理,得AB2-BD2=AD2=AC2-DC2,
故172-x2=102-(21-x)2,
解得x=15.
此时DC=21-x=21-15=6.
所以AD2=102-62=82,即AD=8.
因此BC边上的高为8.
【方法技巧】利用勾股定理求非直角三角形中线段长的方法:作高是构造直角三角形的主要方法,作出三角形一边上的高,将其转化为两个直角三角形,然后利用勾股定理并结合已知条件,采用列方程的方法解决问题.构造直角三角形的原则是:尽量不要分割已知的边和特殊角.
【培优训练】
8.(14分)在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),△ABC为锐角三角形时,小明猜想a2+b2>c2,理由如下:如图(2)
设CD=x,在Rt△ADC中,AD2=b2-x2,
在Rt△ADB中,AD2=c2-(a-x)2,
则b2-x2=c2-(a-x)2,∴a2+b2=c2+2ax,
∵a>0,x>0,∴2ax>0,∴a2+b2>c2,
∴当△ABC为锐角三角形时,a2+b2>c2.
所以小明的猜想是正确的.
(1)请你猜想,当△ABC为钝角三角形时,a2+b2与c2的大小关系.
(2)温馨提示:在图(3)中,作AC边上的高.
(3)证明你猜想的结论是否正确.
【解析】(1)若△ABC是钝角三角形,∠C为钝角,则有a2+b2(2)如图所示:
(3)当△ABC是钝角三角形时,a2+b2证明:如图,过点B作BD⊥AC,交AC的延长线于点D.
设CD为x,则有DB2=a2-x2,根据勾股定理得(b+x)2+a2-x2=c2,即b2+2bx+x2+a2-x2=c2,
∴a2+b2+2bx=c2,
∵b>0,x>0,∴2bx>0,∴a2+b2
(第1课时)
(30分钟 50分)
一、选择题(每小题4分,共12分)
1.(2017·沧州期末)在Rt△ABC中,斜边BC=2,则AB2+AC2+BC2的值为 ( )
A.8 B.4 C.6 D.无法计算
【解析】选A.因为在Rt△ABC中,BC为斜边,
所以AB2+AC2=BC2,
所以AB2+AC2+BC2=2BC2=2×22=8.
2.如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为
( )
A.4S1 B.4S2
C.4S2+S3 D.3S1+4S3
【解析】选A.设等腰直角三角形的直角边为a,正方形边长为c,
则S2=(a+c)(a-c)=a2-c2,
∴S2=S1-S3,
∴S3=2S1-2S2,
∴平行四边形面积=2S1+2S2+S3=2S1+2S2+2S1-2S2=4S1.
3.(2017·东光县一模)如图,在Rt△ABC中,∠ACB=90°,BC=12,AC=5,分别以点A,B为圆心,大于线段AB长度的一半为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连接CD,则△ACD的周长为 ( )
A.13 B.17 C.18 D.25
【解析】选C.∵∠ACB=90°,BC=12,AC=5,∴AB==13,根据题意可得EF是AB的垂直平分线,∴D是AB的中点,AD=AB=6.5,CD=AB=6.5,∴△ACD的周长为13+5=18.
二、填空题(每小题4分,共12分)
4.(2017·孝义市期中)如图,字母B所代表的正方形的面积是________.
【解析】由题可知,在直角三角形中,斜边的平方=169,一直角边的平方=25,根据勾股定理知,另一直角边的平方=169-25=144,即字母B所代表的正方形的面积是144.
答案:144
5.(2017·丽水中考)我国三国时期数学家赵爽为了证明勾股定理,创造了一副“弦图”,后人称其为“赵爽弦图”,如图1所示.在图2中,若正方形ABCD的边长为14,正方形IJKL的边长为2,且IJ∥AB,则正方形EFGH的边长为________.
【解析】一个直角三角形的面积为(14×14-2×2)÷8=(196-4)÷8=192÷8=24,
正方形EFGH的面积为24×4+2×2=96+4=100,
所以正方形EFGH的边长为=10.
答案:10
6.(2017·路北区期中)在△ABC中,AB=15,AC=13,高AD=12,则△ABC中BC边的长为________.
【解析】(1)如图,在锐角△ABC中,AC=13,AB=15,BC边上高AD=12,
∵在Rt△ACD中AC=13,AD=12,
∴CD2=AC2-AD2=132-122=25,
∴CD=5,
∵在Rt△ABD中,AB=15,AD=12,由勾股定理得
BD2=AB2-AD2=152-122=81,
∴BD=9,
∴BC的长为BD+DC=9+5=14.
(2)在钝角△ABC中,AC=13,AB=15,BC边上高AD=12,
在Rt△ACD中AC=13,AD=12,
由勾股定理得
CD2=AC2-AD2=132-122=25,
∴CD=5,
在Rt△ABD中AB=15,AD=12,由勾股定理得
BD2=AB2-AD2=152-122=81,
∴BD=9,
∴BC的长为BD-DC=9-5=4.
答案:4或14
【变式训练】在Rt△ABC中,∠BAC=90°,AB=AC=2.以AC为一边,在△ABC外部作等腰Rt△ACD,则线段BD的长为________.
【解析】首先要结合题意,画出相应的图形.因为以AC为一边在△ABC外部作等腰Rt△ACD,则AC可以是直角边,也可以是斜边,所以有三种情况:
如图1,BD=4;如图2,BD==2;如图3,∠ACD=90°,
BC=2,CD=,BD==.
答案:4或2或
三、解答题(共26分)
7.(12分)如图,
已知△ABC中,BC=21,AC=10,AB=17,求BC边上的高.
【解析】如图,
过点A作AD⊥BC,垂足为点D.在Rt△ABD与Rt△ACD中,设BD=x,则DC=21-x,由勾股定理,得AB2-BD2=AD2=AC2-DC2,
故172-x2=102-(21-x)2,
解得x=15.
此时DC=21-x=21-15=6.
所以AD2=102-62=82,即AD=8.
因此BC边上的高为8.
【方法技巧】利用勾股定理求非直角三角形中线段长的方法:作高是构造直角三角形的主要方法,作出三角形一边上的高,将其转化为两个直角三角形,然后利用勾股定理并结合已知条件,采用列方程的方法解决问题.构造直角三角形的原则是:尽量不要分割已知的边和特殊角.
【培优训练】
8.(14分)在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),△ABC为锐角三角形时,小明猜想a2+b2>c2,理由如下:如图(2)
设CD=x,在Rt△ADC中,AD2=b2-x2,
在Rt△ADB中,AD2=c2-(a-x)2,
则b2-x2=c2-(a-x)2,∴a2+b2=c2+2ax,
∵a>0,x>0,∴2ax>0,∴a2+b2>c2,
∴当△ABC为锐角三角形时,a2+b2>c2.
所以小明的猜想是正确的.
(1)请你猜想,当△ABC为钝角三角形时,a2+b2与c2的大小关系.
(2)温馨提示:在图(3)中,作AC边上的高.
(3)证明你猜想的结论是否正确.
【解析】(1)若△ABC是钝角三角形,∠C为钝角,则有a2+b2
(3)当△ABC是钝角三角形时,a2+b2
设CD为x,则有DB2=a2-x2,根据勾股定理得(b+x)2+a2-x2=c2,即b2+2bx+x2+a2-x2=c2,
∴a2+b2+2bx=c2,
∵b>0,x>0,∴2bx>0,∴a2+b2
