2017-2018学年八年级数学下册第17章勾股定理17.1勾股定理一课一练基础闯关2(含解析)
文档属性
| 名称 | 2017-2018学年八年级数学下册第17章勾股定理17.1勾股定理一课一练基础闯关2(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 381.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-19 00:00:00 | ||
图片预览


文档简介
勾股定理
一课一练·基础闯关
题组勾股定理在实际中的应用
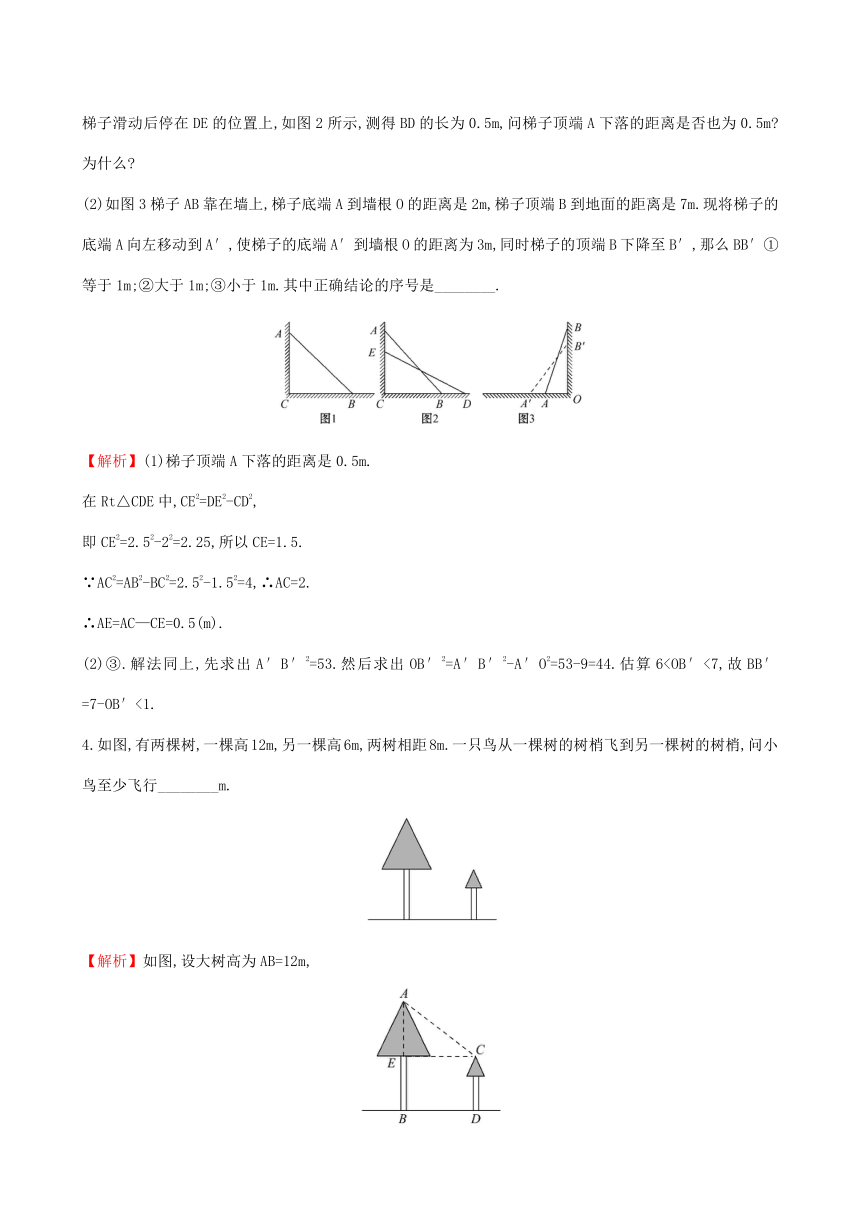
1.要登上某建筑物,靠墙有一架梯子,底端离建筑物5m,顶端离地面12m,则梯子的长度为 ( )
A.12m B.13m C.14m D.15m
【解析】选B.如图所示:
由题意AC=12m,BC=5m,
∴在Rt△ABC中,AB==13(m).
2.(2017·重庆期中)如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了________步路(假设2步为1m),却踩伤了花草( )
A.1 B.2 C.3 D.4
【解析】选D.由勾股定理,得路==5(m),少走(3+4-5)×2=4(步).
3.(2017·枝江市期中)如图,一根长5米的竹竿AB斜靠在一竖直的墙AO上,这时AO为4米,如果竹竿的顶端A沿墙下滑1米,那么竹竿底端B外移的距离BD ( )
A.等于1米 B.大于1米
C.小于1米 D.以上都不对
【解析】选A.由题意得:在Rt△AOB中,OA=4米,AB=5米,∴OB==
3米,在Rt△COD中,OC=3米,CD=5米,∴OD==4米,∴BD=OD-OB=1米.
【变式训练】(1)如图1,一个梯子AB长2.5m,顶端A靠在墙AC上,这时梯子下端B与墙根C距离为1.5m,梯子滑动后停在DE的位置上,如图2所示,测得BD的长为0.5m,问梯子顶端A下落的距离是否也为0.5m?为什么?
(2)如图3梯子AB靠在墙上,梯子底端A到墙根O的距离是2m,梯子顶端B到地面的距离是7m.现将梯子的底端A向左移动到A′,使梯子的底端A′到墙根O的距离为3m,同时梯子的顶端B下降至B′,那么BB′①等于1m;②大于1m;③小于1m.其中正确结论的序号是________.
【解析】(1)梯子顶端A下落的距离是0.5m.
在Rt△CDE中,CE2=DE2-CD2,
即CE2=2.52-22=2.25,所以CE=1.5.
∵AC2=AB2-BC2=2.52-1.52=4,∴AC=2.
∴AE=AC—CE=0.5(m).
(2)③.解法同上,先求出A′B′2=53.然后求出OB′2=A′B′2-A′O2=53-9=44.估算64.如图,有两棵树,一棵高12m,另一棵高6m,两树相距8m.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行________m.
【解析】如图,设大树高为AB=12m,
小树高为CD=6m,
过C点作CE⊥AB于E,则四边形EBDC是矩形,
连接AC,
∴EB=6m,EC=8m,AE=AB-EB=12-6=6(m),
在Rt△AEC中,AC==10(m).
故小鸟至少飞行10m.
答案:10
【变式训练】有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m的一棵大树上,大树高14m,且巢离树顶部1m.当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,赶回巢中,它至少需要__________s.
【解析】如图,由题意知AB=3,
CD=14-1=13,BD=24.
过点A作AE⊥CD于点E.
则CE=13-3=10,AE=24,
所以AC2=CE2+AE2=102+242.
所以AC=26,26÷5=5.2(s).
答案:5.2
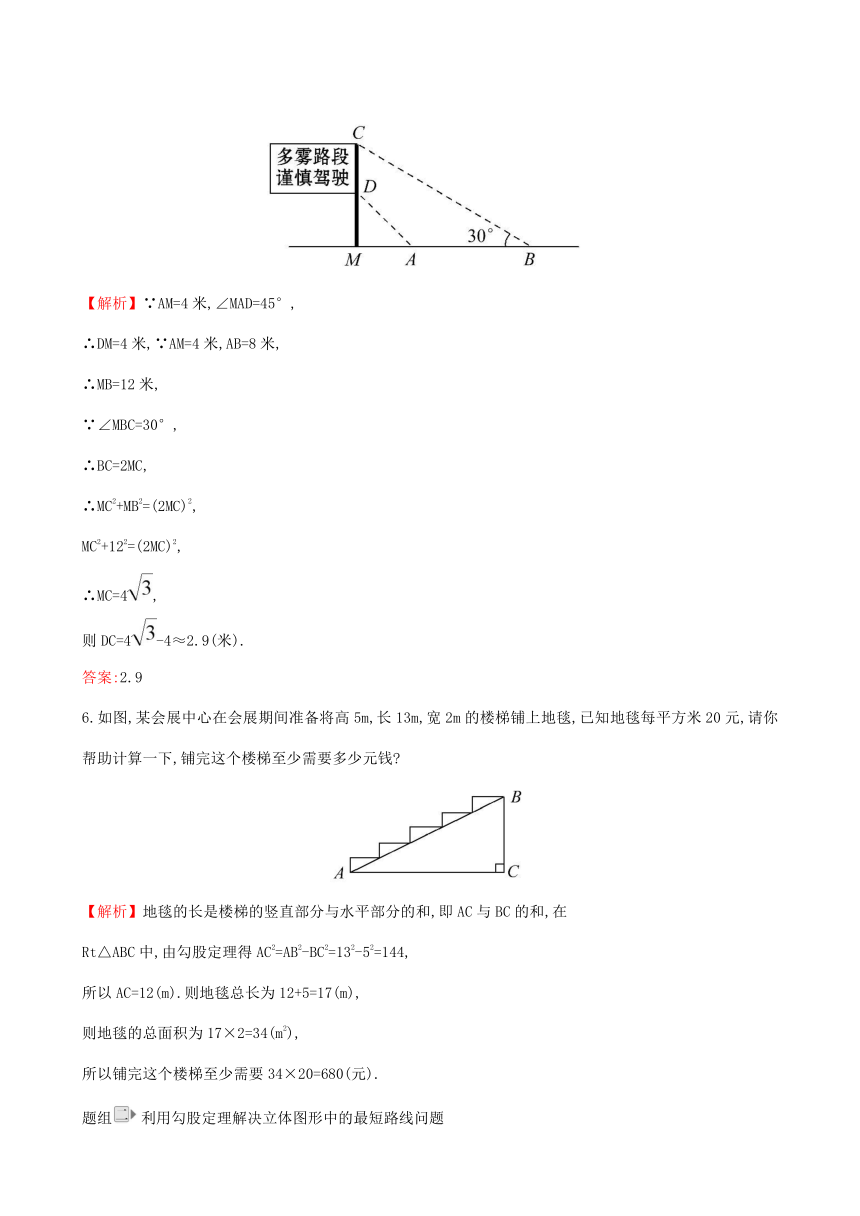
5.如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为________米(结果精确到0.1米,参考数据:≈1.41,≈1.73).
【解析】∵AM=4米,∠MAD=45°,
∴DM=4米,∵AM=4米,AB=8米,
∴MB=12米,
∵∠MBC=30°,
∴BC=2MC,
∴MC2+MB2=(2MC)2,
MC2+122=(2MC)2,
∴MC=4,
则DC=4-4≈2.9(米).
答案:2.9
6.如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼梯铺上地毯,已知地毯每平方米20元,请你帮助计算一下,铺完这个楼梯至少需要多少元钱?
【解析】地毯的长是楼梯的竖直部分与水平部分的和,即AC与BC的和,在
Rt△ABC中,由勾股定理得AC2=AB2-BC2=132-52=144,
所以AC=12(m).则地毯总长为12+5=17(m),
则地毯的总面积为17×2=34(m2),
所以铺完这个楼梯至少需要34×20=680(元).
题组利用勾股定理解决立体图形中的最短路线问题
1.(2017·嘉祥县期中)如图,有一长、宽、高分别为12cm,4cm,3cm的木箱,在它里面放一根细木条(木条的粗细忽略不计),要求细木条不能露出木箱,请你算一算,能放入的细木条的最大长度是 ( )
A.13 cm B.14 cm C.15 cm D.16 cm
【解题指南】要判断能否放进去,关键是求得该木箱中的最长线段的长度,通过比较大小作出判断.
【解析】选A.如图,连接AC,AD.
在Rt△ABC中,有AC2=AB2+BC2=160,
在Rt△ACD中,有AD2=AC2+CD2=169,
AD==13(cm),
∴能放进去的细木条的最大长度为13cm.
2.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10 cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是 ( )
A.13 cm B.2cm
C.cm D.2cm
【解析】选A.圆柱侧面展开如图,作点A关于杯口的对称点A′,则AE=A′E=3,连接A′C,A′C的长度即为蚂蚁吃到饭粒需爬行的最短路径.过点C作CB⊥AA′于点B,则BE=9,BC=5,
∴A′B=12,
在Rt△A′BC中,由勾股定理得:
A′C===13,
故蚂蚁到达饭粒的最短路径为13 cm.
【知识归纳】在求解几何体表面两点间最短距离的问题时,通常是将几何体表面展开,求展开图中两点之间的距离,但在展开过程中一定要弄清所要求的是哪两点之间的距离,以及它们在展开图中相应的位置.
【变式训练】如图,已知圆柱底面的周长为4dm,圆柱高为2dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为 ( )
A.4dm B.2dm C.2dm D.4dm
【解析】选A.如图,依题意,得AB=2dm,BC=×4dm=2dm,由勾股定理,得AC=2dm,∴这圈金属丝的周长最小为4dm.
3.如图所示的长方体是某种饮料的纸质包装盒,规格为5×6×10(单位:cm),在上盖中开有一孔便于插吸管,吸管长为13cm,小孔到图中边AB距离为1cm,到上盖中与AB相邻的两边距离相等,设插入吸管后露在盒外面的管长为hcm,则h的最小值大约为________cm.
(精确到个位,参考数据:≈1.4,≈1.7,≈2.2).
【解析】如图所示:连接DC,CF,由题意:ED=3,EC=5-1=4,CD2=32+42=25=52,
CF2=52+102=125,∴吸管口到纸盒内的最大距离为=5≈11cm.
∴hmin=13-11≈2(cm).
答案:2
4.我国古代数学中有这样一道数学题:
有一棵枯树直立在地上,树高2丈,粗3尺,有一根藤条从树根处缠绕而上,缠绕7周到达树顶,(如图)请问这根藤条有多长?
(注:枯树可以看成圆柱;树粗3尺,指的是:圆柱底面周长为3尺,1丈=10尺).
【解题指南】本题是一道古代数学题,由于树可以近似看作圆柱,藤条绕树缠绕,我们可以转化为平面图形来解决.
【解析】如图,在Rt△ABC中,由勾股定理得AB2=BC2+AC2,因为BC=20,AC=3×7=21,
所以AB2=202+212=841,所以AB=29.所以这根藤条有29尺长.
如图,一棵树在一次强台风中,从离地面3m处折断,量得倒下部分树尖与树根的距离是4m,这棵树在折断前的高度是 ( )
A.7 m B.8 m C.9 m D.10 m
【解析】选B.如图所示:
∵△ABC是直角三角形,AB=3m,AC=4m,
∴BC===5(m),
∴大树的高度=AB+BC=3+5=8(m).
【母题变式】[变式一]一旗杆在其的B处折断,量得AC=5m,则旗杆原来的高度为 ( )
A.m B.2m C.10 m D.5m
【解析】选D.设AB=x,由题意可得,AC2=BC2-AB2,即(2x)2-x2=52,解得x=,所以旗杆原来的高度为3x=5m.
[变式二]如图所示,一棵大树高8米,一场大风过后,大树在离地面3米处折断倒下,树的顶端落在地上,则此时树的顶端离树的底部有 ( )
A.4 m B.3.5 m C.5 m D.13.6 m
【解析】选A.∵大树高8m,在离地面3m处折断,
∴AB=3m,AC=8-3=5(m),
∴BC===4(m).
[变式三]如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度(滑轮上方的部分忽略不计)为 ( )
A.12 m B.13 m C.16 m D.17 m
【解析】选D.设旗杆高度为x,则AC=AD=x,AB=(x-2)m,BC=8m,在Rt△ABC中,AB2+BC2=AC2,即(x-2)2+82=x2,解得x=17,即旗杆的高度为17m.
一课一练·基础闯关
题组勾股定理在实际中的应用
1.要登上某建筑物,靠墙有一架梯子,底端离建筑物5m,顶端离地面12m,则梯子的长度为 ( )
A.12m B.13m C.14m D.15m
【解析】选B.如图所示:
由题意AC=12m,BC=5m,
∴在Rt△ABC中,AB==13(m).
2.(2017·重庆期中)如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了________步路(假设2步为1m),却踩伤了花草( )
A.1 B.2 C.3 D.4
【解析】选D.由勾股定理,得路==5(m),少走(3+4-5)×2=4(步).
3.(2017·枝江市期中)如图,一根长5米的竹竿AB斜靠在一竖直的墙AO上,这时AO为4米,如果竹竿的顶端A沿墙下滑1米,那么竹竿底端B外移的距离BD ( )
A.等于1米 B.大于1米
C.小于1米 D.以上都不对
【解析】选A.由题意得:在Rt△AOB中,OA=4米,AB=5米,∴OB==
3米,在Rt△COD中,OC=3米,CD=5米,∴OD==4米,∴BD=OD-OB=1米.
【变式训练】(1)如图1,一个梯子AB长2.5m,顶端A靠在墙AC上,这时梯子下端B与墙根C距离为1.5m,梯子滑动后停在DE的位置上,如图2所示,测得BD的长为0.5m,问梯子顶端A下落的距离是否也为0.5m?为什么?
(2)如图3梯子AB靠在墙上,梯子底端A到墙根O的距离是2m,梯子顶端B到地面的距离是7m.现将梯子的底端A向左移动到A′,使梯子的底端A′到墙根O的距离为3m,同时梯子的顶端B下降至B′,那么BB′①等于1m;②大于1m;③小于1m.其中正确结论的序号是________.
【解析】(1)梯子顶端A下落的距离是0.5m.
在Rt△CDE中,CE2=DE2-CD2,
即CE2=2.52-22=2.25,所以CE=1.5.
∵AC2=AB2-BC2=2.52-1.52=4,∴AC=2.
∴AE=AC—CE=0.5(m).
(2)③.解法同上,先求出A′B′2=53.然后求出OB′2=A′B′2-A′O2=53-9=44.估算6
【解析】如图,设大树高为AB=12m,
小树高为CD=6m,
过C点作CE⊥AB于E,则四边形EBDC是矩形,
连接AC,
∴EB=6m,EC=8m,AE=AB-EB=12-6=6(m),
在Rt△AEC中,AC==10(m).
故小鸟至少飞行10m.
答案:10
【变式训练】有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m的一棵大树上,大树高14m,且巢离树顶部1m.当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,赶回巢中,它至少需要__________s.
【解析】如图,由题意知AB=3,
CD=14-1=13,BD=24.
过点A作AE⊥CD于点E.
则CE=13-3=10,AE=24,
所以AC2=CE2+AE2=102+242.
所以AC=26,26÷5=5.2(s).
答案:5.2
5.如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为________米(结果精确到0.1米,参考数据:≈1.41,≈1.73).
【解析】∵AM=4米,∠MAD=45°,
∴DM=4米,∵AM=4米,AB=8米,
∴MB=12米,
∵∠MBC=30°,
∴BC=2MC,
∴MC2+MB2=(2MC)2,
MC2+122=(2MC)2,
∴MC=4,
则DC=4-4≈2.9(米).
答案:2.9
6.如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼梯铺上地毯,已知地毯每平方米20元,请你帮助计算一下,铺完这个楼梯至少需要多少元钱?
【解析】地毯的长是楼梯的竖直部分与水平部分的和,即AC与BC的和,在
Rt△ABC中,由勾股定理得AC2=AB2-BC2=132-52=144,
所以AC=12(m).则地毯总长为12+5=17(m),
则地毯的总面积为17×2=34(m2),
所以铺完这个楼梯至少需要34×20=680(元).
题组利用勾股定理解决立体图形中的最短路线问题
1.(2017·嘉祥县期中)如图,有一长、宽、高分别为12cm,4cm,3cm的木箱,在它里面放一根细木条(木条的粗细忽略不计),要求细木条不能露出木箱,请你算一算,能放入的细木条的最大长度是 ( )
A.13 cm B.14 cm C.15 cm D.16 cm
【解题指南】要判断能否放进去,关键是求得该木箱中的最长线段的长度,通过比较大小作出判断.
【解析】选A.如图,连接AC,AD.
在Rt△ABC中,有AC2=AB2+BC2=160,
在Rt△ACD中,有AD2=AC2+CD2=169,
AD==13(cm),
∴能放进去的细木条的最大长度为13cm.
2.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10 cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是 ( )
A.13 cm B.2cm
C.cm D.2cm
【解析】选A.圆柱侧面展开如图,作点A关于杯口的对称点A′,则AE=A′E=3,连接A′C,A′C的长度即为蚂蚁吃到饭粒需爬行的最短路径.过点C作CB⊥AA′于点B,则BE=9,BC=5,
∴A′B=12,
在Rt△A′BC中,由勾股定理得:
A′C===13,
故蚂蚁到达饭粒的最短路径为13 cm.
【知识归纳】在求解几何体表面两点间最短距离的问题时,通常是将几何体表面展开,求展开图中两点之间的距离,但在展开过程中一定要弄清所要求的是哪两点之间的距离,以及它们在展开图中相应的位置.
【变式训练】如图,已知圆柱底面的周长为4dm,圆柱高为2dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为 ( )
A.4dm B.2dm C.2dm D.4dm
【解析】选A.如图,依题意,得AB=2dm,BC=×4dm=2dm,由勾股定理,得AC=2dm,∴这圈金属丝的周长最小为4dm.
3.如图所示的长方体是某种饮料的纸质包装盒,规格为5×6×10(单位:cm),在上盖中开有一孔便于插吸管,吸管长为13cm,小孔到图中边AB距离为1cm,到上盖中与AB相邻的两边距离相等,设插入吸管后露在盒外面的管长为hcm,则h的最小值大约为________cm.
(精确到个位,参考数据:≈1.4,≈1.7,≈2.2).
【解析】如图所示:连接DC,CF,由题意:ED=3,EC=5-1=4,CD2=32+42=25=52,
CF2=52+102=125,∴吸管口到纸盒内的最大距离为=5≈11cm.
∴hmin=13-11≈2(cm).
答案:2
4.我国古代数学中有这样一道数学题:
有一棵枯树直立在地上,树高2丈,粗3尺,有一根藤条从树根处缠绕而上,缠绕7周到达树顶,(如图)请问这根藤条有多长?
(注:枯树可以看成圆柱;树粗3尺,指的是:圆柱底面周长为3尺,1丈=10尺).
【解题指南】本题是一道古代数学题,由于树可以近似看作圆柱,藤条绕树缠绕,我们可以转化为平面图形来解决.
【解析】如图,在Rt△ABC中,由勾股定理得AB2=BC2+AC2,因为BC=20,AC=3×7=21,
所以AB2=202+212=841,所以AB=29.所以这根藤条有29尺长.
如图,一棵树在一次强台风中,从离地面3m处折断,量得倒下部分树尖与树根的距离是4m,这棵树在折断前的高度是 ( )
A.7 m B.8 m C.9 m D.10 m
【解析】选B.如图所示:
∵△ABC是直角三角形,AB=3m,AC=4m,
∴BC===5(m),
∴大树的高度=AB+BC=3+5=8(m).
【母题变式】[变式一]一旗杆在其的B处折断,量得AC=5m,则旗杆原来的高度为 ( )
A.m B.2m C.10 m D.5m
【解析】选D.设AB=x,由题意可得,AC2=BC2-AB2,即(2x)2-x2=52,解得x=,所以旗杆原来的高度为3x=5m.
[变式二]如图所示,一棵大树高8米,一场大风过后,大树在离地面3米处折断倒下,树的顶端落在地上,则此时树的顶端离树的底部有 ( )
A.4 m B.3.5 m C.5 m D.13.6 m
【解析】选A.∵大树高8m,在离地面3m处折断,
∴AB=3m,AC=8-3=5(m),
∴BC===4(m).
[变式三]如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度(滑轮上方的部分忽略不计)为 ( )
A.12 m B.13 m C.16 m D.17 m
【解析】选D.设旗杆高度为x,则AC=AD=x,AB=(x-2)m,BC=8m,在Rt△ABC中,AB2+BC2=AC2,即(x-2)2+82=x2,解得x=17,即旗杆的高度为17m.
