青岛版九年级下册数学 第5章对函数的再探索 单元检测(含答案)
文档属性
| 名称 | 青岛版九年级下册数学 第5章对函数的再探索 单元检测(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 124.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-18 00:00:00 | ||
图片预览


文档简介
第5章对函数的再探索
一、选择题
1.若y=mx2+nx﹣p(其中m,n,p是常数)为二次函数,则( )
A.?m,n,p均不为0????????????????????B.?m≠0,且n≠0????????????????????C.?m≠0????????????????????D.?m≠0,或p≠0
2.下列各式中,y是x的二次函数的是( )
A.?y=???????????????????????????B.?y=x2+x﹣2???????????????????????????C.?y=2x+1???????????????????????????D.?y2=x2+3x
3.将抛物线y=3x2向左平移2个单位,再向下平移1个单位,所得抛物线为( ?).
A.?y=3(x+2)2-1??????????????????B.?y=3(x-2)2+1??????????????????C.?y=3(x-2)2-1??????????????????D.?y=3(x+2)2+l
4.已知点( )、( )、( )在双曲线 上,当 时, 、 、 的大小关系是(?? )
A.?????????????????????B.???????????????????????C.?????????????????????D.?
5.二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论: ①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大. 其中正确的结论有(?? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
6.抛物线y=(x+2)2﹣3可以由抛物线y=x2平移得到,则下列平移过程正确的是(?? )
A.?先向左平移2个单位,再向上平移3个单位???????????B.?先向左平移2个单位,再向下平移3个单位 C.?先向右平移2个单位,再向下平移3个单位???????????D.?先向右平移2个单位,再向上平移3个单位
7.下列函数中,不是二次函数的是( )
A.?y=1﹣x2???????????????B.?y=2x2+4??????????????C.?y=(x﹣1)(x+4)?????????????D.?y=(x﹣2)2﹣x2
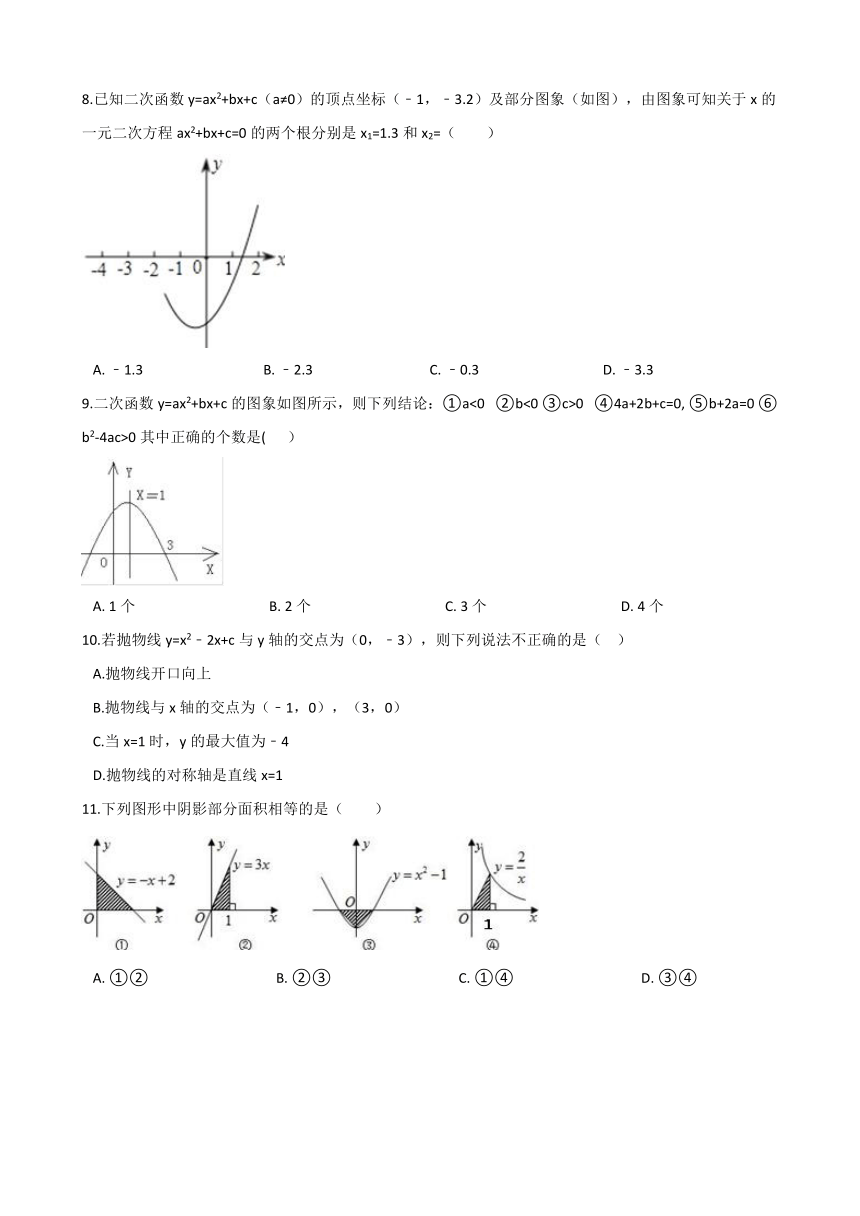
8.已知二次函数y=ax2+bx+c(a≠0)的顶点坐标(﹣1,﹣3.2)及部分图象(如图),由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=1.3和x2=( )
A.?﹣1.3???????????????????????????????????B.?﹣2.3??????????????????????????????????C.?﹣0.3????????????????????????????????????D.?﹣3.3
9.二次函数y=ax2+bx+c的图象如图所示,则下列结论:①a<0???②b<0?③c>0???④4a+2b+c=0,?⑤b+2a=0?⑥ b2-4ac>0其中正确的个数是(???? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
10.若抛物线y=x2﹣2x+c与y轴的交点为(0,﹣3),则下列说法不正确的是(?? )
A.抛物线开口向上 B.抛物线与x轴的交点为(﹣1,0),(3,0) C.当x=1时,y的最大值为﹣4 D.抛物线的对称轴是直线x=1
11.下列图形中阴影部分面积相等的是( )
A.?①②?????????????????????????????????????B.?②③?????????????????????????????????????C.?①④?????????????????????????????????????D.?③④
12.已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的近似解为( )
A.?x1≈﹣2.1,x2≈0.1?????????B.?x1≈﹣2.5,x2≈0.5?????????C.?x1≈﹣2.9,x2≈0.9?????????D.?x1≈﹣3,x2≈1
二、填空题
13.已知y与 成反比例,当y=1时,x=4,则当x=2时,y=________.
14.一位运动员投掷铅球,如果铅球运行时离地面的高度为y(米)关于水平距离x(米)的函数解析式为y=﹣ x2+x+, 那么铅球运动过程中最高点离地面的距离为________?米.
15.二次函数y=4x2+3的顶点坐标为________?.
16.把二次函数的表达式y=x2-4x+6化为y=a(x-h)2+k的形式,那么h+k=________.
17.如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x﹣m)2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标最大值为________?.
18.若函数y=4x与y=的图象有一个交点是(, 2),则另一个交点坐标是________?
19.反比例函数y=﹣ ,当y的值小于﹣3时,x的取值范围是________.
20.如图,一次函数与反比例的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围是________.
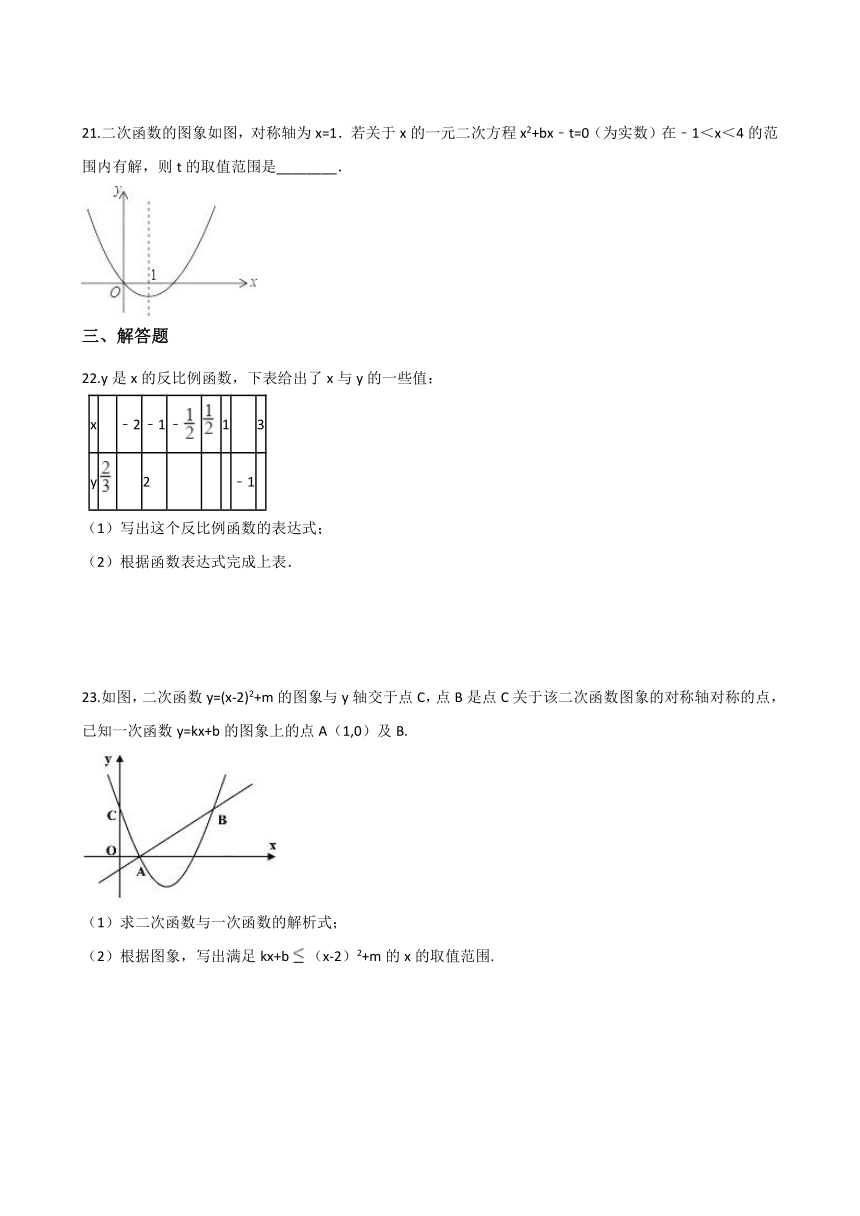
21.二次函数的图象如图,对称轴为x=1.若关于x的一元二次方程x2+bx﹣t=0(为实数)在﹣1<x<4的范围内有解,则t的取值范围是________.
三、解答题
22.y是x的反比例函数,下表给出了x与y的一些值:
x
﹣2
﹣1
﹣
1
3
y
2
﹣1
(1)写出这个反比例函数的表达式; (2)根据函数表达式完成上表.
23.如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象上的点A(1,0)及B. (1)求二次函数与一次函数的解析式; (2)根据图象,写出满足kx+b(x-2)2+m的x的取值范围.
24.如图,顶点M在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由;
(3)把抛物线与直线y=x的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点
25.如图,抛物线y=ax2+bx+c交x轴于A(﹣4,0),B(1,0),交y轴于C点,且OC=2OB.
(1)求抛物线的解析式;
(2)在直线BC上找点D,使△ABD为以AB为腰的等腰三角形,求D点的坐标.
(3)在抛物线上是否存在异于B的点P,过P点作PQ⊥AC于Q,使△APQ与△ABC相似?若存在,请求出P点坐标;若不存在,请说明理由.
参考答案
一、选择题
C B A B B B D D D C D B
二、填空题
13.
14. 3
15. (0,3)
16. 4
17. 8
18.
19. 0<x<1
20. x<﹣1或0<x<2
21. ﹣1≤t<8
三、解答题
22. 解:(1)设反比例函数的表达式为y=,把x=﹣1,y=2代入得k=﹣2,y=﹣. (2)将y=代入得:x=﹣3; 将x=﹣2代入得:y=1; 将x=﹣代入得:y=4; 将x=代入得:y=﹣4, 将x=1代入得:y=﹣2; 将y=﹣1代入得:x=2, 将x=3代入得:y=﹣. 故答案为:﹣3;1;4;﹣4;﹣2;2;-.
23. 解;(1)将点A(1,0)代入y=(x-2)2+m得(1-2)2+m=0,解得m=-1, 所以二次函数解析式为y=(x-2)2-1; 当x=0时,y=4-1=3, 所以C点坐标为(0,3), 由于C和B关于对称轴对称,而抛物线的对称轴为直线x=2, 所以B点坐标为(4,3), 将A(1,0)、B(4,3)代入y=kx+b得 ,解得, 所以一次函数解析式为y=x-1; (2)观察图像可得x的取值范围:x≤1或x≥4.
24. (1)解:∵A点为直线y=x+1与x轴的交点, ∴A(﹣1,0), 又B点横坐标为2,代入y=x+1可求得y=3, ∴B(2,3), ∵抛物线顶点在y轴上, ∴可设抛物线解析式为y=ax2+c, 把A、B两点坐标代入可得 ,解得 , ∴抛物线解析式为y=x2﹣1; (2)解:△ABM为直角三角形.理由如: 由(1)抛物线解析式为y=x2﹣1可知M点坐标为(0,﹣1), ∴AM= ,AB= = =3 ,BM= =2 , ∴AM2+AB2=2+18=20=BM2 , ∴△ABM为直角三角形 (3)解:当抛物线y=x2﹣1平移后顶点坐标为(m,2m)时,其解析式为y=(x﹣m)2+2m,即y=x2﹣2mx+m2+2m, 联立y=x,可得 ,消去y整理可得x2﹣(2m+1)x+m2+2m=0, ∵平移后的抛物线总有不动点, ∴方程x2﹣(2m+1)x+m2+2m=0总有实数根, ∴△≥0,即(2m+1)2﹣4(m2+2m)≥0, 解得m≤ , 即当m≤ 时,平移后的抛物线总有不动点
25. (1)解:∵B(1,0),OC=2OB, ∴C(0,﹣2), 设抛物线解析式为y=a(x+4)(x﹣1), 把C(0,﹣2)代入得a?4?(﹣1)=﹣2,解得a= , ∴抛物线的解析式为y= (x+4)(x﹣1),即y= x2+ x﹣2 (2)解:AB=1﹣(﹣4)=5, 设直线BC的解析式为:y=kx+b, 把B(1,0),C(0,﹣2)代入得 ,解得 , ∴直线BC的解析式为y=2x﹣2, 设D(m,2m﹣2), ∵△ABD为以AB为腰的等腰三角形, ∴BD=BA=5或AD=AB=5, 当BD=BA时,即(m﹣1)2+(2m﹣2)2=52 , 解得m1=1+ ,m2=1﹣ ,此时D点坐标为(1+ ,2 ),(1﹣ ,﹣2 ), 当AD=AB时,即(m+4)2+(2m﹣2)2=52 , 解得m1=1(舍去),m2=﹣1,此时D点坐标为(﹣1,﹣4), 综上所述,满足条件的D点坐标为(1+ ,2 ),(1﹣ ,﹣2 ),(﹣1,﹣4) (3)解:AB2=25,BC2=12+22=5,AC2=42+22=20, ∵AB2=BC2+AC2 , ∴△ABC为直角三角形,∠ACB=90°, ∵∠BAC=∠CAO, ∴△ACO∽△ABC, ∵△APQ与△ABC相似, ∴∠CAP=∠OAC, ∴AC平分∠BAP, 设直线AP交y轴于E,作CF⊥AE于F, 则CF=CO=2, ∵∠CEF=∠AEO, ∴△ECF∽△EAO, ∴ = = = , 在Rt△AOE中,∵OE2+OA2=AE2 , ∴(2+CE)2+42=(2CE)2 , 解得CE=﹣2(舍去)或CE= , ∴E(0,﹣ ), 设直线AE的解析式为y=mx+n, 把A(﹣4,0),E(0,﹣ )得 ,解得 , ∴直线AE的解析式为y=﹣ x﹣ , 解方程组 ,解得 或 , ∴P(﹣ ,﹣ ).
