2017-2018学年下学期高二数学(理)人教版(期中复习)每日一题2018年4月19日+生活中的优化问题
文档属性
| 名称 | 2017-2018学年下学期高二数学(理)人教版(期中复习)每日一题2018年4月19日+生活中的优化问题 |  | |
| 格式 | zip | ||
| 文件大小 | 449.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-18 23:22:39 | ||
图片预览



文档简介
4月19日 生活中的优化问题
高考频度:★★★☆☆ 难易程度:★★★☆☆
学霸推荐
1.某公司的盈利y(元)和时间x(天)的函数关系是y=f(x),且f'(100)=-1,这个数据说明在第100天时
A.公司已经亏损 B.公司的盈利在增加
C.公司的盈利在逐渐减少 D.公司有时盈利有时亏损
2.某工厂要建造一个长方体状的无盖箱子,其容积为48 m3,高为3 m,如果箱底每平方米的造价为15元,箱壁每平方米的造价为12元,那么箱子的最低总造价为
A.900元 B.840元
C.818元 D.816元
3.张师傅欲将一球形的石材工件削砍加工成一圆柱形的新工件,已知原球形工件的半径为,则张师傅的材料利用率的最大值等于(注:材料利用率=)
A. B.
C. D.
4.某厂将原油精炼为汽油,需对原油进行冷却和加热,如果第x小时,原油温度(单位:℃)为f(x)=x3-x2+8
(0≤x≤5),那么,原油温度的瞬时变化率的最小值是
A.8 B.
C.-1 D.-8
5.要做一个圆锥形漏斗,其母线长为20cm,要使其体积最大,则高为
A.cm B.cm
C.cm D.cm
6.某旅行社在暑假期间推出如下旅游团组团办法:达到100人的团体,每人收费1000元.如果团体的人数超过100人,那么每超过1人,每人平均收费降低5元,但团体人数不能超过180人(不到100人不组团),要使旅行社的收费最多,则旅游团组团人数为
A.130 B.140
C.150 D.160
7.某公司在甲、乙两地销售同一种品牌的汽车,利润(单位:万元)分别为和,其中x为销售量(单位:辆).若该公司在两地共销售15辆汽车,则该公司能获得的最大利润为__________万元.
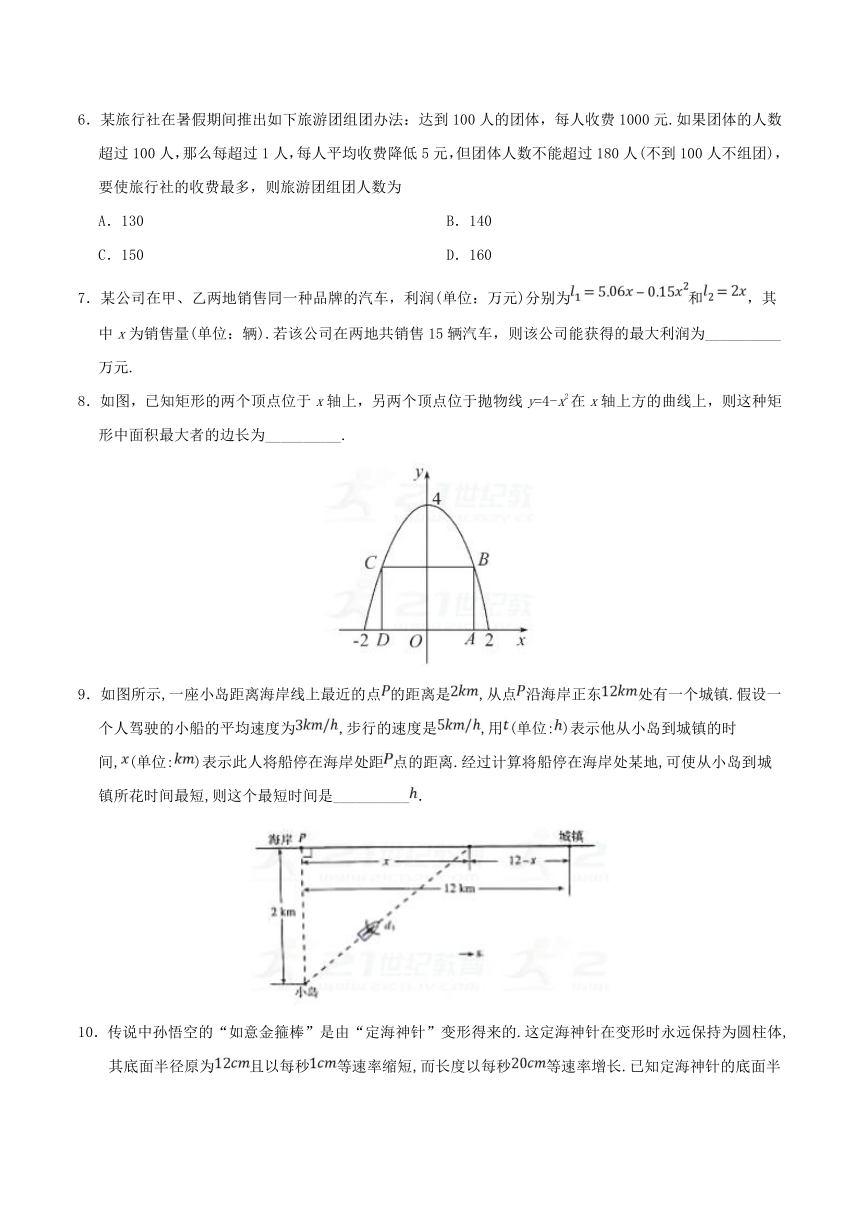
8.如图,已知矩形的两个顶点位于x轴上,另两个顶点位于抛物线y=4-x2在x轴上方的曲线上,则这种矩形中面积最大者的边长为__________.
9.如图所示,一座小岛距离海岸线上最近的点的距离是,从点沿海岸正东处有一个城镇.假设一个人驾驶的小船的平均速度为,步行的速度是,用(单位:)表示他从小岛到城镇的时间,(单位:)表示此人将船停在海岸处距点的距离.经过计算将船停在海岸处某地,可使从小岛到城镇所花时间最短,则这个最短时间是__________.
10.传说中孙悟空的“如意金箍棒”是由“定海神针”变形得来的.这定海神针在变形时永远保持为圆柱体,其底面半径原为且以每秒等速率缩短,而长度以每秒等速率增长.已知定海神针的底面半径只能从缩到为止,且知在这段变形过程中,当底面半径为时其体积最大.假设孙悟空将定海神针体积最小时定形成金箍棒,则此时金箍棒的底面半径为__________.
11.某工厂利用辐射对食品进行灭菌消毒,现准备在该厂附近建一职工宿舍,并对宿舍进行防辐射处理,建房防辐射材料的选用与宿舍到工厂的距离有关.若建造宿舍的所有费用(万元)和宿舍与工厂的距离的关系为:.为了交通方便,工厂与宿舍之间还要修一条简易便道,已知修路每公里成本为万元,工厂一次性补贴职工交通费万元.设为建造宿舍、修路费用与给职工的补贴之和.
(1)求的表达式;
(2)宿舍应建在离工厂多远处,可使总费用最小,并求最小值.
12.某地环保部门跟踪调查一种有害昆虫的数量.根据调查数据,该昆虫的数量(万只)与时间(年)(其中)的关系为.为有效控制有害昆虫数量、保护生态环境,环保部门通过实时监控比值(其中为常数,且)来进行生态环境分析.
(1)当时,求比值取最小值时的值;
(2)经过调查,环保部门发现:当比值不超过时不需要进行环境防护.为确保恰好3年不需要进行保护,求实数的取值范围.(为自然对数的底数,)
13.一块圆柱形木料的底面半径为12cm,高为32cm,要将这块木料加工成一只毛笔筒,在木料一端正中间掏去一个小圆柱,使小圆柱与原木料同轴,并且掏取的圆柱体积是原木料体积的三分之一,设小圆柱底面半径为r,高为h,要求笔筒底面的厚度超过2cm.
(1)求r与h的关系,并指出r的取值范围;
(2)笔筒成形后进行后续加工,要求笔筒上底圆环面、桶内侧面、外表侧面都喷上油漆,其中,上底圆环面、外表侧面喷漆费用均为a(元/cm2),桶内侧面喷漆费用为2a (元/ cm2),而桶内底面铺贴金属薄片,其费用是7a (元/ cm2)(其中a为正常数).
①将笔筒的后续加工费用y (元)表示为r的函数;
②求出当r取何值时,能使笔筒的后续加工费用y最小,并求出y的最小值.
1.【答案】C
【解析】因为f'(100)=-1,所以函数图象在x=100处的切线的斜率为负值,说明公司的盈利在逐渐减少.
2.【答案】D
【解析】设箱底一边的长度为x m,箱子的总造价为 l元,
根据题意,得l=15×+12×2(3x+)=240+72(x+)(x>0), l'=72(1-).
令l'=0,解得x=4或x=-4(舍去).
当04时,l'>0.
故当x=4时,l有最小值,为816.
故当箱底是边长为 4 m 的正方形时,箱子的总造价最低,最低总造价为816元.
4.【答案】C
【解析】由题意,f′(x)=x2-2x=(x-1)2-1,因为0≤x≤5,所以x=1时,f′(x)的最小值为-1,即原油温度的瞬时变化率的最小值是-1,故选C.
5.【答案】D
【解析】设高为hcm,底面半径为rcm,则h2+r2=400.又体积V=πr2h,则V=π(400-h2)h,
令V′=0,得唯一极值点h=,此时体积最大,故选D.
6.【答案】C
【解析】设参加旅游的人数为x,旅游团收费为f(x),则依题意有f(x)=1000x-5(x-100)x (100≤x≤180),
令f′(x)=1500-10x=0,得x=150,
又f(100)=100000,f(150)=112500,f(180)=108000,
所以当参加人数为150时,旅游团的收费最多,可达112500元,故选C.
7.【答案】45.6
【解析】设在甲地销售汽车m辆,则在乙地销售汽车(15-m)辆,总利润y=5.06m-0.15m2+2(15-m)=-0.15m2+3.06m+30(0≤m≤15,m∈N).求导数,得y′=-0.3m+3.06.令y′=0,解得m=10.2.当0≤m<10.2时, y′>0;当10.2<m≤15时,y′<0.
故当m=10.2时,y取得极大值,也是最大值.
由于m为自然数,且当m=10时,y=45.6;当m=11时,y=45.51.
所以当公司在甲地销售汽车10辆,在乙地销售汽车5辆时,该公司获得的利润最大,最大利润为45.6万元.
8.【答案】和
【解析】设点B(x,4-x2)(0令S′=0,得x=,故当一边长为,另一边长为时,S=-2x3+8x取得最大值.
9.【答案】
【解析】由题意知,所花时间,求导得,令
,解得,当时,;当时,,所以当时,取得最小值,此时,即最短时间为h.
10.【答案】4
【解析】设定海神针原长度为.经过秒体积最小,且.
体积.
所以.
由题意得时.
解得.代入,得.
所以当时,;当时,.
又当时,;当时,,
所以当,即底面半径为时体积最小.
11.【解析】(1)由题意得,
整理得.
12.【解析】(1)当时,,
∴.
列表得:
2
0
单调递减
极小值
单调递增
∴在上单调递减,在上单调递增,∴在时取得最小值.
(2),根据(1)知在上单调递减,在上单调递增,
∵确保恰好3年不需要进行保护,∴,解得.
故实数的取值范围为.
(2)①根据题意,得笔筒的后续加工费用,
整理得,即定义域为.
②由①知,,
令,得,列表如下:
单调递减
极小值
单调递增
由表知,当时,取得极小值,即最小值,为..
故当时,能使笔筒的后续加工费用最小,最小值为元.
高考频度:★★★☆☆ 难易程度:★★★☆☆
学霸推荐
1.某公司的盈利y(元)和时间x(天)的函数关系是y=f(x),且f'(100)=-1,这个数据说明在第100天时
A.公司已经亏损 B.公司的盈利在增加
C.公司的盈利在逐渐减少 D.公司有时盈利有时亏损
2.某工厂要建造一个长方体状的无盖箱子,其容积为48 m3,高为3 m,如果箱底每平方米的造价为15元,箱壁每平方米的造价为12元,那么箱子的最低总造价为
A.900元 B.840元
C.818元 D.816元
3.张师傅欲将一球形的石材工件削砍加工成一圆柱形的新工件,已知原球形工件的半径为,则张师傅的材料利用率的最大值等于(注:材料利用率=)
A. B.
C. D.
4.某厂将原油精炼为汽油,需对原油进行冷却和加热,如果第x小时,原油温度(单位:℃)为f(x)=x3-x2+8
(0≤x≤5),那么,原油温度的瞬时变化率的最小值是
A.8 B.
C.-1 D.-8
5.要做一个圆锥形漏斗,其母线长为20cm,要使其体积最大,则高为
A.cm B.cm
C.cm D.cm
6.某旅行社在暑假期间推出如下旅游团组团办法:达到100人的团体,每人收费1000元.如果团体的人数超过100人,那么每超过1人,每人平均收费降低5元,但团体人数不能超过180人(不到100人不组团),要使旅行社的收费最多,则旅游团组团人数为
A.130 B.140
C.150 D.160
7.某公司在甲、乙两地销售同一种品牌的汽车,利润(单位:万元)分别为和,其中x为销售量(单位:辆).若该公司在两地共销售15辆汽车,则该公司能获得的最大利润为__________万元.
8.如图,已知矩形的两个顶点位于x轴上,另两个顶点位于抛物线y=4-x2在x轴上方的曲线上,则这种矩形中面积最大者的边长为__________.
9.如图所示,一座小岛距离海岸线上最近的点的距离是,从点沿海岸正东处有一个城镇.假设一个人驾驶的小船的平均速度为,步行的速度是,用(单位:)表示他从小岛到城镇的时间,(单位:)表示此人将船停在海岸处距点的距离.经过计算将船停在海岸处某地,可使从小岛到城镇所花时间最短,则这个最短时间是__________.
10.传说中孙悟空的“如意金箍棒”是由“定海神针”变形得来的.这定海神针在变形时永远保持为圆柱体,其底面半径原为且以每秒等速率缩短,而长度以每秒等速率增长.已知定海神针的底面半径只能从缩到为止,且知在这段变形过程中,当底面半径为时其体积最大.假设孙悟空将定海神针体积最小时定形成金箍棒,则此时金箍棒的底面半径为__________.
11.某工厂利用辐射对食品进行灭菌消毒,现准备在该厂附近建一职工宿舍,并对宿舍进行防辐射处理,建房防辐射材料的选用与宿舍到工厂的距离有关.若建造宿舍的所有费用(万元)和宿舍与工厂的距离的关系为:.为了交通方便,工厂与宿舍之间还要修一条简易便道,已知修路每公里成本为万元,工厂一次性补贴职工交通费万元.设为建造宿舍、修路费用与给职工的补贴之和.
(1)求的表达式;
(2)宿舍应建在离工厂多远处,可使总费用最小,并求最小值.
12.某地环保部门跟踪调查一种有害昆虫的数量.根据调查数据,该昆虫的数量(万只)与时间(年)(其中)的关系为.为有效控制有害昆虫数量、保护生态环境,环保部门通过实时监控比值(其中为常数,且)来进行生态环境分析.
(1)当时,求比值取最小值时的值;
(2)经过调查,环保部门发现:当比值不超过时不需要进行环境防护.为确保恰好3年不需要进行保护,求实数的取值范围.(为自然对数的底数,)
13.一块圆柱形木料的底面半径为12cm,高为32cm,要将这块木料加工成一只毛笔筒,在木料一端正中间掏去一个小圆柱,使小圆柱与原木料同轴,并且掏取的圆柱体积是原木料体积的三分之一,设小圆柱底面半径为r,高为h,要求笔筒底面的厚度超过2cm.
(1)求r与h的关系,并指出r的取值范围;
(2)笔筒成形后进行后续加工,要求笔筒上底圆环面、桶内侧面、外表侧面都喷上油漆,其中,上底圆环面、外表侧面喷漆费用均为a(元/cm2),桶内侧面喷漆费用为2a (元/ cm2),而桶内底面铺贴金属薄片,其费用是7a (元/ cm2)(其中a为正常数).
①将笔筒的后续加工费用y (元)表示为r的函数;
②求出当r取何值时,能使笔筒的后续加工费用y最小,并求出y的最小值.
1.【答案】C
【解析】因为f'(100)=-1,所以函数图象在x=100处的切线的斜率为负值,说明公司的盈利在逐渐减少.
2.【答案】D
【解析】设箱底一边的长度为x m,箱子的总造价为 l元,
根据题意,得l=15×+12×2(3x+)=240+72(x+)(x>0), l'=72(1-).
令l'=0,解得x=4或x=-4(舍去).
当0
故当x=4时,l有最小值,为816.
故当箱底是边长为 4 m 的正方形时,箱子的总造价最低,最低总造价为816元.
4.【答案】C
【解析】由题意,f′(x)=x2-2x=(x-1)2-1,因为0≤x≤5,所以x=1时,f′(x)的最小值为-1,即原油温度的瞬时变化率的最小值是-1,故选C.
5.【答案】D
【解析】设高为hcm,底面半径为rcm,则h2+r2=400.又体积V=πr2h,则V=π(400-h2)h,
令V′=0,得唯一极值点h=,此时体积最大,故选D.
6.【答案】C
【解析】设参加旅游的人数为x,旅游团收费为f(x),则依题意有f(x)=1000x-5(x-100)x (100≤x≤180),
令f′(x)=1500-10x=0,得x=150,
又f(100)=100000,f(150)=112500,f(180)=108000,
所以当参加人数为150时,旅游团的收费最多,可达112500元,故选C.
7.【答案】45.6
【解析】设在甲地销售汽车m辆,则在乙地销售汽车(15-m)辆,总利润y=5.06m-0.15m2+2(15-m)=-0.15m2+3.06m+30(0≤m≤15,m∈N).求导数,得y′=-0.3m+3.06.令y′=0,解得m=10.2.当0≤m<10.2时, y′>0;当10.2<m≤15时,y′<0.
故当m=10.2时,y取得极大值,也是最大值.
由于m为自然数,且当m=10时,y=45.6;当m=11时,y=45.51.
所以当公司在甲地销售汽车10辆,在乙地销售汽车5辆时,该公司获得的利润最大,最大利润为45.6万元.
8.【答案】和
【解析】设点B(x,4-x2)(0
9.【答案】
【解析】由题意知,所花时间,求导得,令
,解得,当时,;当时,,所以当时,取得最小值,此时,即最短时间为h.
10.【答案】4
【解析】设定海神针原长度为.经过秒体积最小,且.
体积.
所以.
由题意得时.
解得.代入,得.
所以当时,;当时,.
又当时,;当时,,
所以当,即底面半径为时体积最小.
11.【解析】(1)由题意得,
整理得.
12.【解析】(1)当时,,
∴.
列表得:
2
0
单调递减
极小值
单调递增
∴在上单调递减,在上单调递增,∴在时取得最小值.
(2),根据(1)知在上单调递减,在上单调递增,
∵确保恰好3年不需要进行保护,∴,解得.
故实数的取值范围为.
(2)①根据题意,得笔筒的后续加工费用,
整理得,即定义域为.
②由①知,,
令,得,列表如下:
单调递减
极小值
单调递增
由表知,当时,取得极小值,即最小值,为..
故当时,能使笔筒的后续加工费用最小,最小值为元.
