安徽省六安市舒城中学2017-2018学年高一下学期期中考试数学(理)试题
文档属性
| 名称 | 安徽省六安市舒城中学2017-2018学年高一下学期期中考试数学(理)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-19 00:00:00 | ||
图片预览

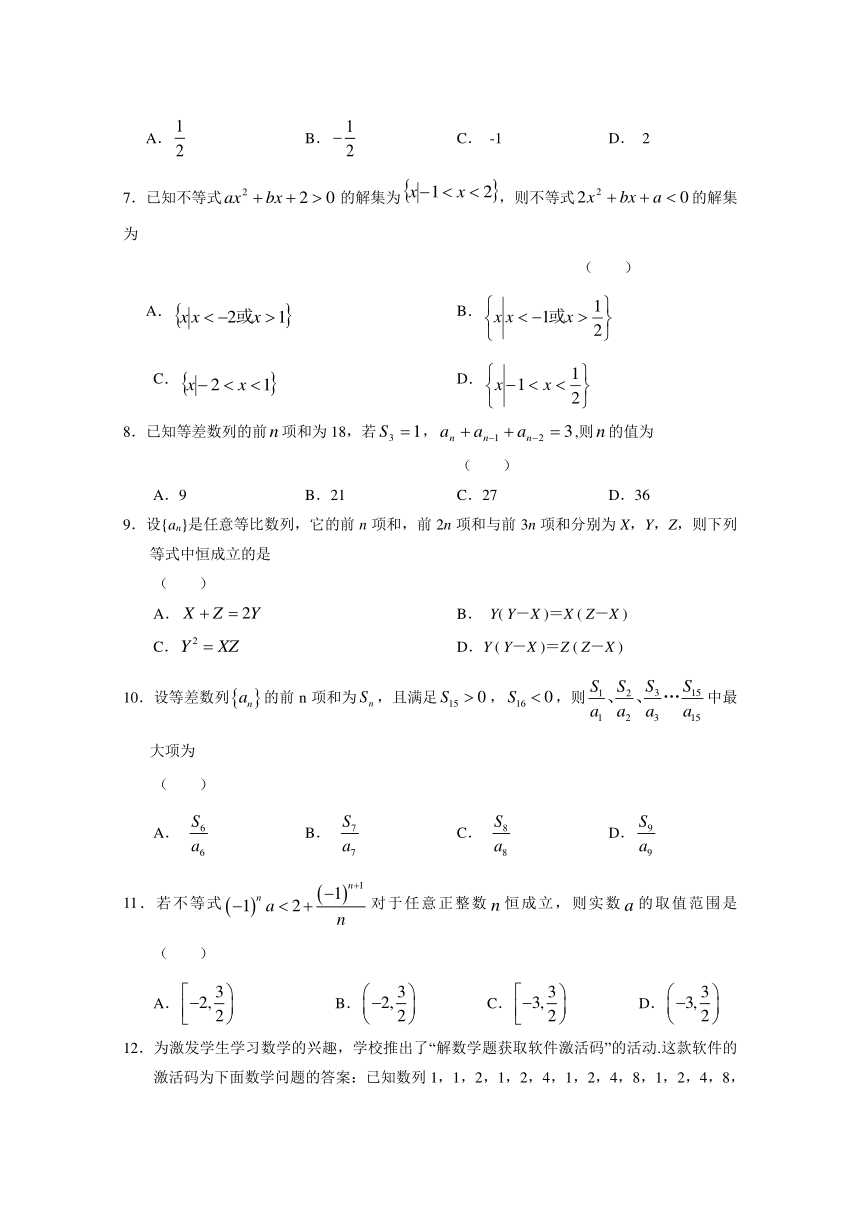


文档简介
舒城中学2017—2018学年度第二学期期中考试
高一理数
(总分:150分 时间:120分钟)
命题: 审校: 磨题:
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(本大题共12个小题,每小题5分,共60分)。
1.若,,为实数,则下列命题正确的是 ( )
A.若,则 B.若,则
C.若,则 D.若,则
2.在等比数列中,,公比,若,则 ( )
A. B. C. D.
3.不等式>0的解集为 ( )
A.(-2,1) B.(2,+∞)
C.(-∞,-2)∪(1,+∞) D.(-2,1)∪(2,+∞)
4.已知等差数列的公差,若,,成等比数列,那么公比为 ( )
A. B. C. D.
5.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为 ( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.由增加的长度决定
6.若等比数列的前项和, 则等于 ( )
A. B. C. -1 D. 2
7.已知不等式的解集为,则不等式的解集为 ( )
A. B.
C. D.
8.已知等差数列的前项和为18,若,,则的值为 ( )
A.9 B.21 C.27 D.36
9.设{an}是任意等比数列,它的前n项和,前2n项和与前3n项和分别为X,Y,Z,则下列等式中恒成立的是 ( )
A. B. Y( Y-X )=X ( Z-X )
C. D.Y ( Y-X )=Z ( Z-X )
10.设等差数列的前n项和为,且满足,,则中最大项为 ( )
A. B. C. D.
11.若不等式对于任意正整数恒成立,则实数的取值范围是 ( )
A. B. C. D.
12.为激发学生学习数学的兴趣,学校推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数且该数列的前项和为2的整数幂.那么该款软件的激活码是 ( )
A.110 B.220 C.330 D.440
二、填空题(本大题共4小题,每小题5分,共20分)
13.不等式的解集为______________ .
14.三角形一边长为14,它对的角为60°,另两边之比为8:5,则此三角形面积为______.
15.数列满足,则=______________ .
16.若关于的不等式的解集中的整数解恰有3个,则实数的取值范围是______________________ .
三、解答题:解答应写出文字说明、证明过程或演算步骤 (本大题共6个小题,共70分)。
17.(本题满分10分)
(Ⅰ)函数(为常数)的定义域为,求实数的取值范围;
(Ⅱ)设为实数,且满足, ,求的取值范围.
18.(本题满分12分)在△中,角的对边分别为,已知,且, .
求: (Ⅰ)角的大小.
(Ⅱ)的面积.
19.(本题满分12分)设是等差数列,是各项都为正数的等比数列,且,, .
(Ⅰ)求,的通项公式;
(Ⅱ)求数列的前项和.
20.(本题满分12分)解关于的不等式.
21.(本题满分12分)某地现有居民住房的总面积为平方米,其中需要拆除的旧住房面积占了一半,当地有关部门决定在每年拆除一定数量旧住房的情况下,仍以的住房增长率建新住房.
(Ⅰ)如果年后该地的住房总面积正好比目前翻一番,那么每年应拆除的旧住房总面积是多少(可取)?
(Ⅱ)在(Ⅰ)的条件下,过年还未拆除的旧住房总面积占当地住房总面积的百分比是多少(保留到小数点后第位)?
22.(本题满分12分)已知为奇函数(是常数),且函数的图象过点.求:
(Ⅰ)求的表达式;
(Ⅱ)定义正数数列,,,求数列的通项公式;
(Ⅲ)已知,设为的前项和,证明:.
高一理数
(总分:150分 时间:120分钟)
命题: 审校: 磨题:
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(本大题共12个小题,每小题5分,共60分)。
1.若,,为实数,则下列命题正确的是 ( )
A.若,则 B.若,则
C.若,则 D.若,则
2.在等比数列中,,公比,若,则 ( )
A. B. C. D.
3.不等式>0的解集为 ( )
A.(-2,1) B.(2,+∞)
C.(-∞,-2)∪(1,+∞) D.(-2,1)∪(2,+∞)
4.已知等差数列的公差,若,,成等比数列,那么公比为 ( )
A. B. C. D.
5.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为 ( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.由增加的长度决定
6.若等比数列的前项和, 则等于 ( )
A. B. C. -1 D. 2
7.已知不等式的解集为,则不等式的解集为 ( )
A. B.
C. D.
8.已知等差数列的前项和为18,若,,则的值为 ( )
A.9 B.21 C.27 D.36
9.设{an}是任意等比数列,它的前n项和,前2n项和与前3n项和分别为X,Y,Z,则下列等式中恒成立的是 ( )
A. B. Y( Y-X )=X ( Z-X )
C. D.Y ( Y-X )=Z ( Z-X )
10.设等差数列的前n项和为,且满足,,则中最大项为 ( )
A. B. C. D.
11.若不等式对于任意正整数恒成立,则实数的取值范围是 ( )
A. B. C. D.
12.为激发学生学习数学的兴趣,学校推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数且该数列的前项和为2的整数幂.那么该款软件的激活码是 ( )
A.110 B.220 C.330 D.440
二、填空题(本大题共4小题,每小题5分,共20分)
13.不等式的解集为______________ .
14.三角形一边长为14,它对的角为60°,另两边之比为8:5,则此三角形面积为______.
15.数列满足,则=______________ .
16.若关于的不等式的解集中的整数解恰有3个,则实数的取值范围是______________________ .
三、解答题:解答应写出文字说明、证明过程或演算步骤 (本大题共6个小题,共70分)。
17.(本题满分10分)
(Ⅰ)函数(为常数)的定义域为,求实数的取值范围;
(Ⅱ)设为实数,且满足, ,求的取值范围.
18.(本题满分12分)在△中,角的对边分别为,已知,且, .
求: (Ⅰ)角的大小.
(Ⅱ)的面积.
19.(本题满分12分)设是等差数列,是各项都为正数的等比数列,且,, .
(Ⅰ)求,的通项公式;
(Ⅱ)求数列的前项和.
20.(本题满分12分)解关于的不等式.
21.(本题满分12分)某地现有居民住房的总面积为平方米,其中需要拆除的旧住房面积占了一半,当地有关部门决定在每年拆除一定数量旧住房的情况下,仍以的住房增长率建新住房.
(Ⅰ)如果年后该地的住房总面积正好比目前翻一番,那么每年应拆除的旧住房总面积是多少(可取)?
(Ⅱ)在(Ⅰ)的条件下,过年还未拆除的旧住房总面积占当地住房总面积的百分比是多少(保留到小数点后第位)?
22.(本题满分12分)已知为奇函数(是常数),且函数的图象过点.求:
(Ⅰ)求的表达式;
(Ⅱ)定义正数数列,,,求数列的通项公式;
(Ⅲ)已知,设为的前项和,证明:.
同课章节目录
