18.1.1 平行四边形的性质 说课课件
图片预览






文档简介
课件16张PPT。八年级 下册 18.1.1 平行四边形的性质(1)一、教材分析 本课是在小学关于平行四边形学习的基础上,进一步得到平行四边形边和角的性质的猜想,并用演绎推理证明猜想,发展理性思维,获得平行四边形的新知识.
它不仅是对已学平行线、三角形等知识的综合应用与深化,也是下一步学习矩形、菱形、正方形与梯形等知识的基础,起着承上启下的作用。(一)本节内容在教材中的地位(二)教学目标
1、理解平行四边形的定义,能根据定义探究平行四边形的性质。
2、利用平行四边形的性质进行有关的证明和计算,解决简单的实际问题。
3、通过观察、猜测、证明,锻炼学生运用数学语言合乎逻辑的进行讨论与质疑,发展学生合理的推理意识,培养主动探究的习惯和勇于探索的创新能力。
重点:平行四边形性质的探究与应用。
难点:平行四边形性质的探究(即如何添加辅助线将平行四边形问题转化为三角形问题来解决的思想方法)二、教法、学法 为突出学生的主体地位,结合“授人以鱼,不如授人以渔”的教学思?想,根据本节课的特点,我带领学生采用自主、合作、探究的学习方式,让学生在自主学习和合作学习中建构平行四边形的性质这一知识体系,同时潜移默化的渗透数形结合、转化等数学思想方法。并设计相应的练习题,让学生在学习中学会思考,学会学习,进一步提高几何演绎推理的能力。 观察这些图片,它们是否都有平行四边形的形象? 你还记得平行四边形的定义吗?
两组对边分别平行的四边形叫做平行四边形.三、教学流程(四个环节)
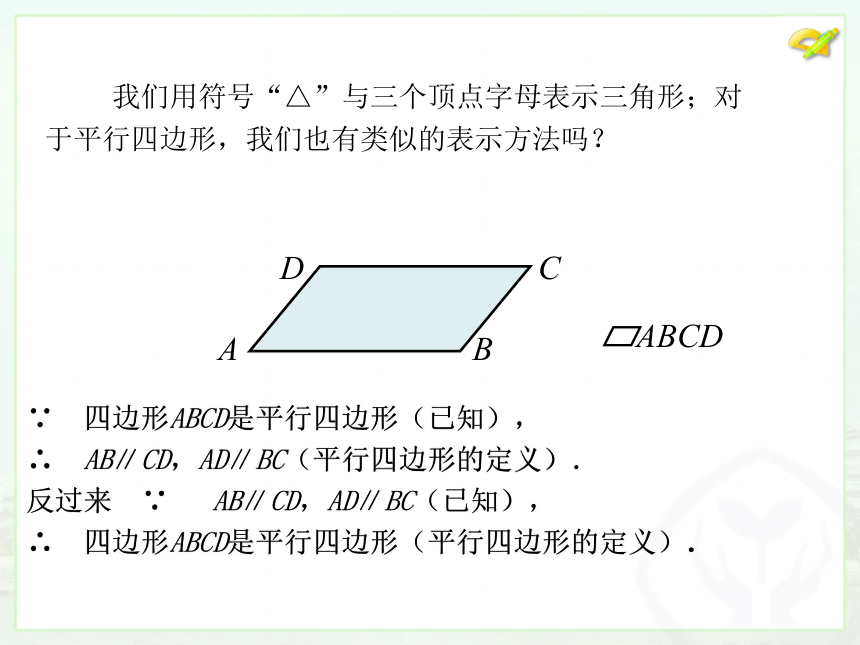
(一)问题驱动∵ 四边形ABCD是平行四边形(已知),
∴ AB∥CD,AD∥BC(平行四边形的定义).
反过来 ∵ AB∥CD,AD∥BC(已知),
∴ 四边形ABCD是平行四边形(平行四边形的定义). 我们用符号“△”与三个顶点字母表示三角形;对
于平行四边形,我们也有类似的表示方法吗? 对于平行四边形,从定义出发,你能得出它的性质
吗? 你能证明这些结论吗? 给出图形定义→研究图形性质→探索图形判定条件 回忆我们的学习经历,研究几何图形的一般思路是
什么? 猜想:平行四边形对角相等,对边相等. (二)自学释疑已知:四边形ABCD是平行四边形.
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.即∠BAD=∠BCD.∵四边形ABCD是平行四边形, ∴AD∥BC ,AB∥CD,∴∠1=∠2,∠3=∠4.∠1=∠2,
AC=CA,
∠3=∠4,∴ △CDA ≌△ABC(ASA),∴ CD=AB, DA=BC, ∠D=∠B又∵∠1=∠2,∠3=∠4,∴∠1+∠4=∠2+∠3, 在△CDA和△ABC中,证明:连接AC(三)反思整合结论:
(3)平行四边形的性质定理:平行四边形的对边相等,
平行四边形的对角相等. 归纳:
(1)有关四边形的问题常常转化为三角形问题解决;
(2)平行四边形的一条对角线把平行四边形分成两个全等的三角形;
这一环节主要培养直观想象与数学建模的核心素养。DE=BF 吗? (四)扩展应用 例2 如图,直线a∥b,A,B为直线a上的任意两
点,点A 到直线b 的距离和点B 到直线b 的距离相等吗?
为什么? 平行线间的距离 【归纳】两条平行线之间的任何平行线段都相等.两条平行线中,一条直线上任意一点到另一条直
线的距离,叫做这两条平行线之间的距离.例3、如图,在□ ABCD中, ∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F的值为( )
A.110° B.30° C.50° D.70°
解析【】选D.在□ABCD中,∠B=110°,∴∠ADC=∠B=110°,∴∠CDF=70°,由三角形外角的性质得,∠E+∠F=70°.例4、(苏州?中考)如图,在平行四边形ABCD中,E是AD边上的中点.若∠ABE=∠EBC,AB=2,则平行四边形ABCD的周长是______.解析:∵四边形ABCD是平行四边形,
∴AD BC,AB DC.
∵∠ABE=∠EBC,
∴∠ABE=∠AEB
∴AB=AE
又E是AD边上的中点,
∴AD=2AE=4
∴平行四边形ABCD的周长为AB+BC+CD+AD=2+4+2+4=12.
答案:12 通过本课时的学习,需要我们掌握:
1、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
2、平行四边形的性质:对边平行 对边相等
对角相等 邻角互补.
3、两条平行线之间的任何平行线段都相等.
4.两条平行线中,一条直线上任意一点到另一条直
线的距离,叫做这两条平行线之间的距离.
课后反思
本节内容看似简单,但要完全理解掌握还是有一定的难度。根据课题理念,本课中我给这一目标的定位是,能够利用定理得到结果,能说出解题思路和大致的过程即可。课中相关的几道习题,就是按照这一理念让学生独立完成或合作完成的。从课堂实际来看,效果也比较好。最后一道检测题是中考原题,目的是引起学生对本节知识的重视和激发学生的兴趣。当然,这节课的设计和执行还存在着缺陷和不足,敬请各位评委批评指正。
它不仅是对已学平行线、三角形等知识的综合应用与深化,也是下一步学习矩形、菱形、正方形与梯形等知识的基础,起着承上启下的作用。(一)本节内容在教材中的地位(二)教学目标
1、理解平行四边形的定义,能根据定义探究平行四边形的性质。
2、利用平行四边形的性质进行有关的证明和计算,解决简单的实际问题。
3、通过观察、猜测、证明,锻炼学生运用数学语言合乎逻辑的进行讨论与质疑,发展学生合理的推理意识,培养主动探究的习惯和勇于探索的创新能力。
重点:平行四边形性质的探究与应用。
难点:平行四边形性质的探究(即如何添加辅助线将平行四边形问题转化为三角形问题来解决的思想方法)二、教法、学法 为突出学生的主体地位,结合“授人以鱼,不如授人以渔”的教学思?想,根据本节课的特点,我带领学生采用自主、合作、探究的学习方式,让学生在自主学习和合作学习中建构平行四边形的性质这一知识体系,同时潜移默化的渗透数形结合、转化等数学思想方法。并设计相应的练习题,让学生在学习中学会思考,学会学习,进一步提高几何演绎推理的能力。 观察这些图片,它们是否都有平行四边形的形象? 你还记得平行四边形的定义吗?
两组对边分别平行的四边形叫做平行四边形.三、教学流程(四个环节)
(一)问题驱动∵ 四边形ABCD是平行四边形(已知),
∴ AB∥CD,AD∥BC(平行四边形的定义).
反过来 ∵ AB∥CD,AD∥BC(已知),
∴ 四边形ABCD是平行四边形(平行四边形的定义). 我们用符号“△”与三个顶点字母表示三角形;对
于平行四边形,我们也有类似的表示方法吗? 对于平行四边形,从定义出发,你能得出它的性质
吗? 你能证明这些结论吗? 给出图形定义→研究图形性质→探索图形判定条件 回忆我们的学习经历,研究几何图形的一般思路是
什么? 猜想:平行四边形对角相等,对边相等. (二)自学释疑已知:四边形ABCD是平行四边形.
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.即∠BAD=∠BCD.∵四边形ABCD是平行四边形, ∴AD∥BC ,AB∥CD,∴∠1=∠2,∠3=∠4.∠1=∠2,
AC=CA,
∠3=∠4,∴ △CDA ≌△ABC(ASA),∴ CD=AB, DA=BC, ∠D=∠B又∵∠1=∠2,∠3=∠4,∴∠1+∠4=∠2+∠3, 在△CDA和△ABC中,证明:连接AC(三)反思整合结论:
(3)平行四边形的性质定理:平行四边形的对边相等,
平行四边形的对角相等. 归纳:
(1)有关四边形的问题常常转化为三角形问题解决;
(2)平行四边形的一条对角线把平行四边形分成两个全等的三角形;
这一环节主要培养直观想象与数学建模的核心素养。DE=BF 吗? (四)扩展应用 例2 如图,直线a∥b,A,B为直线a上的任意两
点,点A 到直线b 的距离和点B 到直线b 的距离相等吗?
为什么? 平行线间的距离 【归纳】两条平行线之间的任何平行线段都相等.两条平行线中,一条直线上任意一点到另一条直
线的距离,叫做这两条平行线之间的距离.例3、如图,在□ ABCD中, ∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F的值为( )
A.110° B.30° C.50° D.70°
解析【】选D.在□ABCD中,∠B=110°,∴∠ADC=∠B=110°,∴∠CDF=70°,由三角形外角的性质得,∠E+∠F=70°.例4、(苏州?中考)如图,在平行四边形ABCD中,E是AD边上的中点.若∠ABE=∠EBC,AB=2,则平行四边形ABCD的周长是______.解析:∵四边形ABCD是平行四边形,
∴AD BC,AB DC.
∵∠ABE=∠EBC,
∴∠ABE=∠AEB
∴AB=AE
又E是AD边上的中点,
∴AD=2AE=4
∴平行四边形ABCD的周长为AB+BC+CD+AD=2+4+2+4=12.
答案:12 通过本课时的学习,需要我们掌握:
1、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
2、平行四边形的性质:对边平行 对边相等
对角相等 邻角互补.
3、两条平行线之间的任何平行线段都相等.
4.两条平行线中,一条直线上任意一点到另一条直
线的距离,叫做这两条平行线之间的距离.
课后反思
本节内容看似简单,但要完全理解掌握还是有一定的难度。根据课题理念,本课中我给这一目标的定位是,能够利用定理得到结果,能说出解题思路和大致的过程即可。课中相关的几道习题,就是按照这一理念让学生独立完成或合作完成的。从课堂实际来看,效果也比较好。最后一道检测题是中考原题,目的是引起学生对本节知识的重视和激发学生的兴趣。当然,这节课的设计和执行还存在着缺陷和不足,敬请各位评委批评指正。
