20.1.2中位数和众数第二课时 课件
图片预览







文档简介
课件23张PPT。20.1.2中位数和众数第二课时1、掌握中位数的概念,会求一组数据的中位数。
2、能应用中位数知识分析解决实际问题。
3、初步感受中位数的特点及其与平均数的区别与联系。 学习重难点重点:掌握中位数的概念,能应用中位数知识分析解决实际问题。 难点:感受中位数的特点及其与平均数的区别与联系。 中位数:中位数是一个位置代表值,利用中位数分析数据可以获得一些信息。
如果已知一组数据的中位数,那么可以知道,小于或大于这个中位数的数据各占一半。将一组数据按照由小到大的顺序排列:如果数据的个数是奇数个,则处于中间位置的数就是这组数据的中位数;如果数据的个数是偶数个,则中间两个数据的平均数就是这组数据的中位数;应用: 快速回答: 下列这组数据的中位数分别是多少? 7 5 4 8 5 8 2 4 8 9 64 5 5 7 8 2 4 6 8 8 9例 题解:(1)先将样本数据按照由小到大的顺序排列:124,129,136,140,145,146,148,154,158,165,175,180则这组数据的中位数为处于中间的两个数146,148的平均数,即: (146+148)÷2=147因此样本数据的中位数是147。 (2)根据(1)中得到的样本数据的结论,可以估计,在这次马拉松比赛中,大约有一半选手的成绩快于147分,有一半选手的成绩慢于147分。这名选手的成绩是142分,快于中位数147分,可以推测他的成绩比一半以上的选手的成绩好。求中位数的一般步骤:1、将这一组数据从小到大(或从大到小)排列;2、若该数据含有奇数个数,位于中间位置的数是中位数;
若该数据含有偶数个数,位于中间两个数的平均数就是中位数。议一议你知道中间位置如何确定吗?n 为奇数时,中间位置是第 个
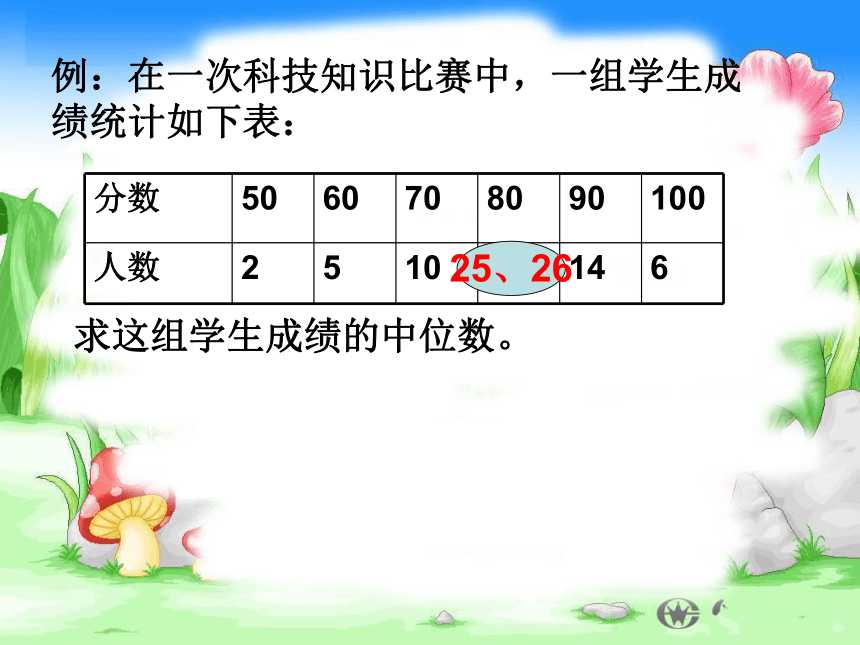
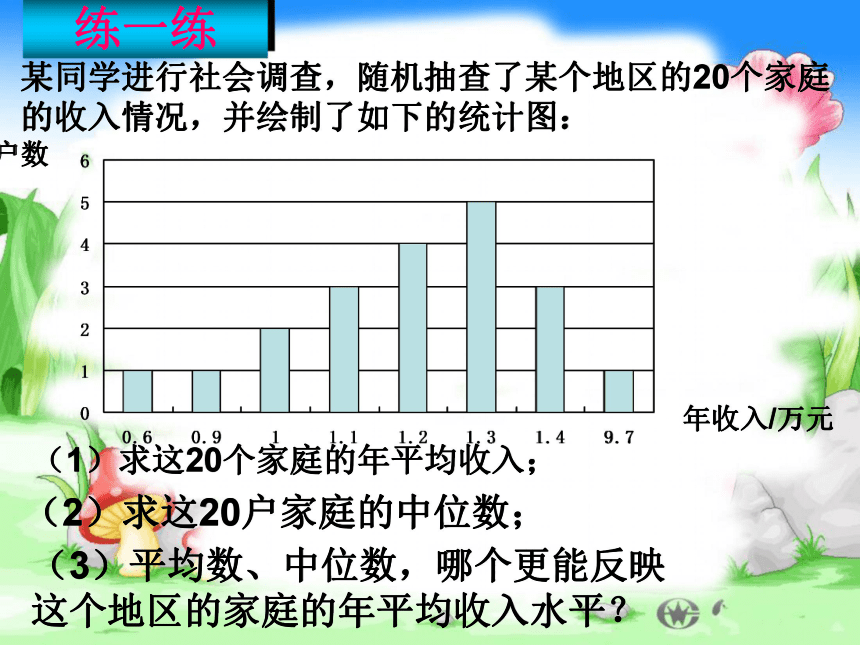
n为偶数时,中间位置是第 , 个例:在一次科技知识比赛中,一组学生成绩统计如下表:求这组学生成绩的中位数。25、26 某同学进行社会调查,随机抽查了某个地区的20个家庭的收入情况,并绘制了如下的统计图:(1)求这20个家庭的年平均收入;(2)求这20户家庭的中位数;(3)平均数、中位数,哪个更能反映这个地区的家庭的年平均收入水平?练一练经理第二天,阿冲上班了。我这里报酬不错, 每周平均工资300元,你在这里好好干!阿冲评评理阿冲在公司工作了一周后平均工资确实是每周300元,你看看公司的工资报表.你欺骗了我,我已经问过公司的职员了,没有一个人是超过300元的经理 阿冲问题1:请大家来评评理,讨论该公司的周平均工资是多少?经理是否欺骗了阿冲?问题2:平均月工资能否客观地反映员工的实际收入?问题3:再仔细观察表中的数据,你们认为用哪个数据
反映一般职员的实际收入比较合适?小测试1、在一次数学竞赛中,5名学生的成绩从低到高排列依 次是 55,57,61,62,98,那么他们的中位数是多少?2、10名工人某天生产同一零件,生产的件数是 15,17,14,10,15,19,17,16,14,12,求这一天10名工人生产的零件的中位数。153、某班一组12人的英语成绩如下:
84,73,89,78,83,86,89,84,100,100,78,100.则这12个数的平均数是_____,中位数是______.4、一组数据按从小到大顺序排列为:13、14、19、x、23、27、28、31,其中位数是22,则x为_______.878521 5、在一组数据0 ,1 ,4,5,8中插入一个数据x,使该组数据的中位数为3,则x=_______26、甲、乙两班举行电脑汉字输入速度比赛,参赛学生每分钟的个数经统计计算后得下表:比较两班的学生成绩的平均水平,优秀率(每分钟输入汉字数≥150个为优秀)的高低。 7、 某教育用个厂生产一批铅球,其重量(单位:km)如下:求这组数据的中位数和平均数。活动与研究 某餐厅共有7名员工,所有员工的工资的情况如下表所示:解答下列问题(1)餐厅所有员工的工资的平均数是多少?(2)所有员工的工资的中位数是多少?(3)用平均数还是中位数,描述该餐厅员工工资的一般水平比较恰当?(4)去掉经理的工资后,其他员工的平均工资是多少元?是否能反映餐厅员工工资的一般水平?平均数、中位数的联系与区别联系:它们从不同角度描述了一组数据的集中趋势。区别:计算平均数时,所有数据都参加运算,它能充分利用数据所提供的信息,但容易受极端值的影响。它应用最为广泛。
中位数的优点是计算简单,只与其在数据中的位置有关。但不能充分利用所有的数据信息。想一想1.数据11, 8, 2, 7, 9, 2, 7, 3, 2, 0, 5中位数是 。
2.数据15, 20, 20, 22,30,30的中位数是 。
3.在数据-1, 0, 4, 5, 8中插入一个数据x ,使得这组数据
的中位数是3,则x= 。
4.数据8, 8, x, 6的众数与平均数相同,那么它们的中位数
是 。
5、10名工人某天生产同一零件,生产的件数是:
15 17 14 10 15
19 17 16 14 12
求这一天10名工人生产的零件的中位数。
6、在一次数学竞赛中,5名学生的成绩从低分到高分排列名次是:
55 57 61 62 98
那么,它们的中位数是多少?
你收获了什么?知识小结:这节课我们学习了中位数的概念,了解了它们
在描述一组数据“平均水平” 时的不同角度和适用范围。方法小结: 求中位数时,首先要先排序(从小到大或从
大到小),然后计算中位数的序号,分数据为奇数个与偶数个两种来求.(既找出最中间的一个数据或最中间两个数并算出它们的平均数)。3. 中位数仅与数据的排列位置有关,某些数据的变动对它的中位数没有影响。当一组数据中的个别数据变动较大时,可用它来描述其集中趋势。作业1、P144练习
2、实践作业:
为了了解开展“孝敬父母,从家务事做起”活动的实施
情况, 抽取本班50名学生,调查他们一周做家务所用时间,得到一组数据,并绘制成下表,请根据下表完成各题:
1)填写图中未完成的部分;
2)该班学生每周做家务的平均时间是 。 3)这组数据的中位数是 。
4)请你根据(2),(3)的结果,用一句话谈谈自己的感受.谢谢指导
2、能应用中位数知识分析解决实际问题。
3、初步感受中位数的特点及其与平均数的区别与联系。 学习重难点重点:掌握中位数的概念,能应用中位数知识分析解决实际问题。 难点:感受中位数的特点及其与平均数的区别与联系。 中位数:中位数是一个位置代表值,利用中位数分析数据可以获得一些信息。
如果已知一组数据的中位数,那么可以知道,小于或大于这个中位数的数据各占一半。将一组数据按照由小到大的顺序排列:如果数据的个数是奇数个,则处于中间位置的数就是这组数据的中位数;如果数据的个数是偶数个,则中间两个数据的平均数就是这组数据的中位数;应用: 快速回答: 下列这组数据的中位数分别是多少? 7 5 4 8 5 8 2 4 8 9 64 5 5 7 8 2 4 6 8 8 9例 题解:(1)先将样本数据按照由小到大的顺序排列:124,129,136,140,145,146,148,154,158,165,175,180则这组数据的中位数为处于中间的两个数146,148的平均数,即: (146+148)÷2=147因此样本数据的中位数是147。 (2)根据(1)中得到的样本数据的结论,可以估计,在这次马拉松比赛中,大约有一半选手的成绩快于147分,有一半选手的成绩慢于147分。这名选手的成绩是142分,快于中位数147分,可以推测他的成绩比一半以上的选手的成绩好。求中位数的一般步骤:1、将这一组数据从小到大(或从大到小)排列;2、若该数据含有奇数个数,位于中间位置的数是中位数;
若该数据含有偶数个数,位于中间两个数的平均数就是中位数。议一议你知道中间位置如何确定吗?n 为奇数时,中间位置是第 个
n为偶数时,中间位置是第 , 个例:在一次科技知识比赛中,一组学生成绩统计如下表:求这组学生成绩的中位数。25、26 某同学进行社会调查,随机抽查了某个地区的20个家庭的收入情况,并绘制了如下的统计图:(1)求这20个家庭的年平均收入;(2)求这20户家庭的中位数;(3)平均数、中位数,哪个更能反映这个地区的家庭的年平均收入水平?练一练经理第二天,阿冲上班了。我这里报酬不错, 每周平均工资300元,你在这里好好干!阿冲评评理阿冲在公司工作了一周后平均工资确实是每周300元,你看看公司的工资报表.你欺骗了我,我已经问过公司的职员了,没有一个人是超过300元的经理 阿冲问题1:请大家来评评理,讨论该公司的周平均工资是多少?经理是否欺骗了阿冲?问题2:平均月工资能否客观地反映员工的实际收入?问题3:再仔细观察表中的数据,你们认为用哪个数据
反映一般职员的实际收入比较合适?小测试1、在一次数学竞赛中,5名学生的成绩从低到高排列依 次是 55,57,61,62,98,那么他们的中位数是多少?2、10名工人某天生产同一零件,生产的件数是 15,17,14,10,15,19,17,16,14,12,求这一天10名工人生产的零件的中位数。153、某班一组12人的英语成绩如下:
84,73,89,78,83,86,89,84,100,100,78,100.则这12个数的平均数是_____,中位数是______.4、一组数据按从小到大顺序排列为:13、14、19、x、23、27、28、31,其中位数是22,则x为_______.878521 5、在一组数据0 ,1 ,4,5,8中插入一个数据x,使该组数据的中位数为3,则x=_______26、甲、乙两班举行电脑汉字输入速度比赛,参赛学生每分钟的个数经统计计算后得下表:比较两班的学生成绩的平均水平,优秀率(每分钟输入汉字数≥150个为优秀)的高低。 7、 某教育用个厂生产一批铅球,其重量(单位:km)如下:求这组数据的中位数和平均数。活动与研究 某餐厅共有7名员工,所有员工的工资的情况如下表所示:解答下列问题(1)餐厅所有员工的工资的平均数是多少?(2)所有员工的工资的中位数是多少?(3)用平均数还是中位数,描述该餐厅员工工资的一般水平比较恰当?(4)去掉经理的工资后,其他员工的平均工资是多少元?是否能反映餐厅员工工资的一般水平?平均数、中位数的联系与区别联系:它们从不同角度描述了一组数据的集中趋势。区别:计算平均数时,所有数据都参加运算,它能充分利用数据所提供的信息,但容易受极端值的影响。它应用最为广泛。
中位数的优点是计算简单,只与其在数据中的位置有关。但不能充分利用所有的数据信息。想一想1.数据11, 8, 2, 7, 9, 2, 7, 3, 2, 0, 5中位数是 。
2.数据15, 20, 20, 22,30,30的中位数是 。
3.在数据-1, 0, 4, 5, 8中插入一个数据x ,使得这组数据
的中位数是3,则x= 。
4.数据8, 8, x, 6的众数与平均数相同,那么它们的中位数
是 。
5、10名工人某天生产同一零件,生产的件数是:
15 17 14 10 15
19 17 16 14 12
求这一天10名工人生产的零件的中位数。
6、在一次数学竞赛中,5名学生的成绩从低分到高分排列名次是:
55 57 61 62 98
那么,它们的中位数是多少?
你收获了什么?知识小结:这节课我们学习了中位数的概念,了解了它们
在描述一组数据“平均水平” 时的不同角度和适用范围。方法小结: 求中位数时,首先要先排序(从小到大或从
大到小),然后计算中位数的序号,分数据为奇数个与偶数个两种来求.(既找出最中间的一个数据或最中间两个数并算出它们的平均数)。3. 中位数仅与数据的排列位置有关,某些数据的变动对它的中位数没有影响。当一组数据中的个别数据变动较大时,可用它来描述其集中趋势。作业1、P144练习
2、实践作业:
为了了解开展“孝敬父母,从家务事做起”活动的实施
情况, 抽取本班50名学生,调查他们一周做家务所用时间,得到一组数据,并绘制成下表,请根据下表完成各题:
1)填写图中未完成的部分;
2)该班学生每周做家务的平均时间是 。 3)这组数据的中位数是 。
4)请你根据(2),(3)的结果,用一句话谈谈自己的感受.谢谢指导
