19.2.2一次函数第一课时 课件
图片预览






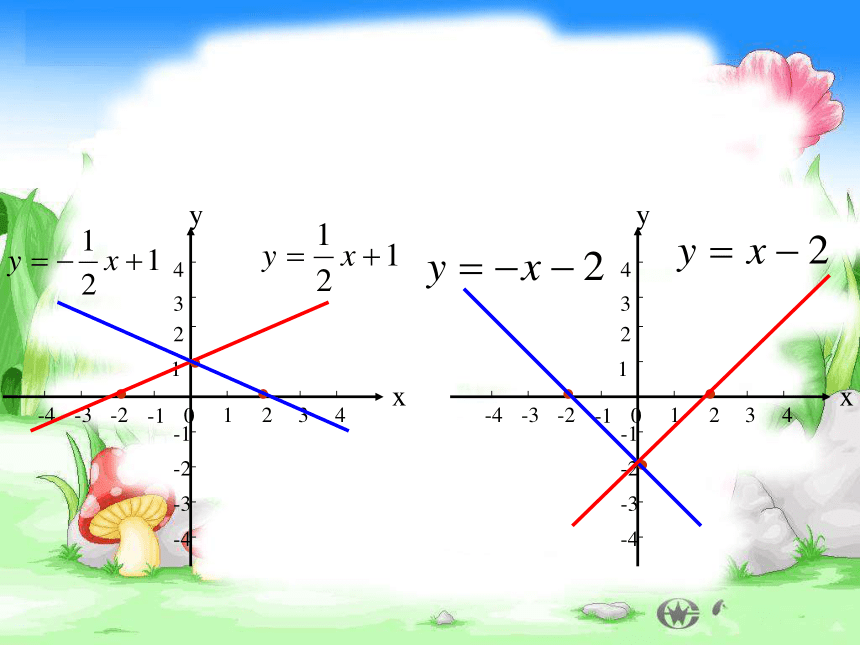
文档简介
课件23张PPT。19.2.2一次函数1.掌握一次函数解析式的特点及意义,知道一次函数与正比例函数关系.
2.通过类比的方法学习一次函数,体会数学研究方法多样性.进一步提高分析概括、总结归纳能力. 学习重难点重点:.一次函数解析式特点. 难点:一次函数与正比例函数关系. 小测:
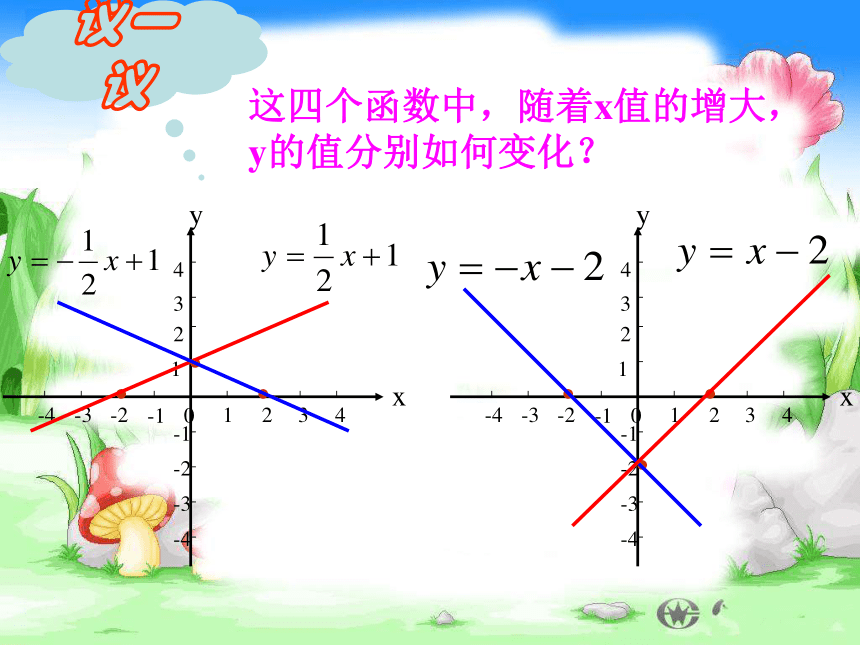
在平面直角坐标系中画出下列函数 的图象:
( 1 )( 2 )( 3 )( 4 )······
这四个函数中,随着x值的增大,
y的值分别如何变化?议一议一次函数y=kx+b有下列性质:
?
(1) 当k>0时,y随x的增大而增大,这时函数的图象从左到右上升;
?
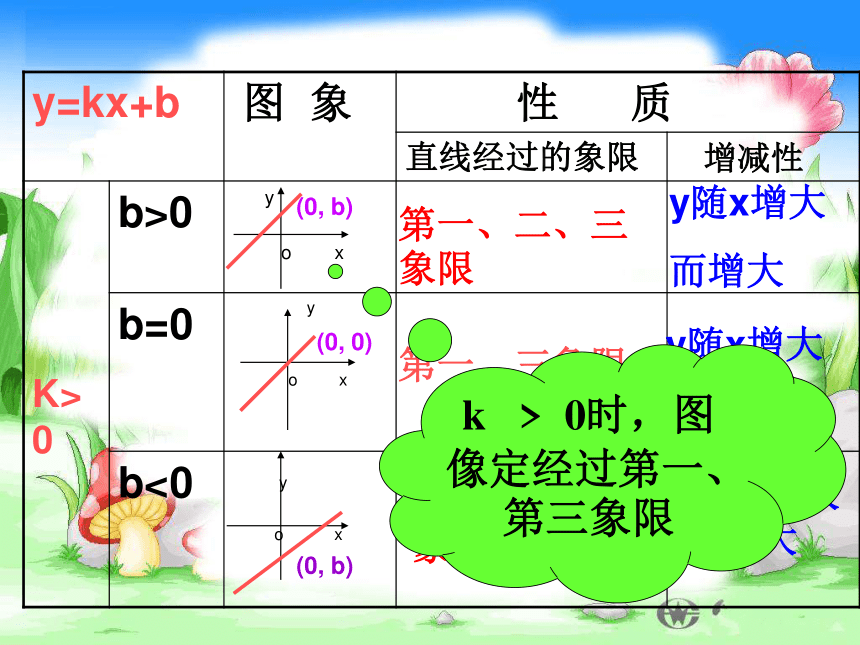
(2) 当k<0时,y随x的增大而_____,这时函数的图象从左到右_____. 概括减小下降一次函数y=kx+b的图像与k、b的关系······第一、三象限y随x增大而增大 第一、二、三象限y随x增大
而增大第一、三、四象限y随x增大而增大(0, b)(0, b)(0, 0)k > 0时,图像定经过第一、第三象限第二、四象限y随x增大
而减小第一、二、四象限y随x增大
而减小第二、三、四象限y随x增大
而减小(0, b)(o, b)(0, 0)k < 0时,图像定经过第二、第四象限热身练习:判断下列各图中的函数k、b的符号. k > 0 b >0 k < 0 b >0 k > 0 b < 0001. 一次函数 的图象经过 象限。y随x的增大而 ,它的图象与x轴、y轴的坐标分别为___________________。
2.函数y=(k-1)x+2,当k>1时,y随x的增大而______,当k<1时,y随x的增大而_____。
一、二、四减小(2,0)增大减小小试牛刀(0,4) 画出函数y=-2x+2的图象,结合图象
回答下列问题:
(1)?? 这个函数中,随着x的增大,y将增大
还是减小?
它的图象从左到右怎样变化?
(2)?? 当x取何值时,y=0?
当x取何值时,y>0?
当0
做一做Y=-2x+2 看y=-2x+2的图象,随x的值增大,y的值有怎样的变化趋势? 当x取何值 时,y=0?
当x取何值时,y>0?
当0(1,0)例 题例1、已知函数y=(m+1)x-3
(1)当m取何值时,y随x的增大而增大?
这时它的图象经过哪些象限?
(2)当 m取何值时,y随x的增大而减小?
这时它的图象经过哪些象限?1.已知函数y=(m-3)x-2/3. (1)?当m取何值时,y随x的增大而增大? (2) 当m取何值时,y随x的增大而减小? 课堂练习:例 题例2、对于一次函数y=(a+4)x+2a-1,如果
y随x的增大而增大,且它的图象与y轴的
交点在x轴的下方,试求a的取值范围拓展与应用1.一次函数y=kx+b中,kb>0,且y随x的增大而
减小,则它的图象大致为( )2:已知一次函数y=(1-2m)x+m-1,若函数y随x的增大而减小,并且函数的图象经过二、三、四象限,求m的取值范围.3:已知一次函数y=(3m-8)x+1-m图象与y轴交点在x轴下方,且y随x的增大而减小,其中m为整数. (1)求m的值;(2)当x取何值时,0<y<4?一次函数中k与b的正、负与它的图象经过的象限归纳列表为: 试一试 (2)、(4) 创设情境一次函数的图象是一条直线,一般情况下我们画一次函数的图象,取哪两个点比较简便? (0,b)(-b/k,0)和再见!
2.通过类比的方法学习一次函数,体会数学研究方法多样性.进一步提高分析概括、总结归纳能力. 学习重难点重点:.一次函数解析式特点. 难点:一次函数与正比例函数关系. 小测:
在平面直角坐标系中画出下列函数 的图象:
( 1 )( 2 )( 3 )( 4 )······
这四个函数中,随着x值的增大,
y的值分别如何变化?议一议一次函数y=kx+b有下列性质:
?
(1) 当k>0时,y随x的增大而增大,这时函数的图象从左到右上升;
?
(2) 当k<0时,y随x的增大而_____,这时函数的图象从左到右_____. 概括减小下降一次函数y=kx+b的图像与k、b的关系······第一、三象限y随x增大而增大 第一、二、三象限y随x增大
而增大第一、三、四象限y随x增大而增大(0, b)(0, b)(0, 0)k > 0时,图像定经过第一、第三象限第二、四象限y随x增大
而减小第一、二、四象限y随x增大
而减小第二、三、四象限y随x增大
而减小(0, b)(o, b)(0, 0)k < 0时,图像定经过第二、第四象限热身练习:判断下列各图中的函数k、b的符号. k > 0 b >0 k < 0 b >0 k > 0 b < 0001. 一次函数 的图象经过 象限。y随x的增大而 ,它的图象与x轴、y轴的坐标分别为___________________。
2.函数y=(k-1)x+2,当k>1时,y随x的增大而______,当k<1时,y随x的增大而_____。
一、二、四减小(2,0)增大减小小试牛刀(0,4) 画出函数y=-2x+2的图象,结合图象
回答下列问题:
(1)?? 这个函数中,随着x的增大,y将增大
还是减小?
它的图象从左到右怎样变化?
(2)?? 当x取何值时,y=0?
当x取何值时,y>0?
当0
做一做Y=-2x+2 看y=-2x+2的图象,随x的值增大,y的值有怎样的变化趋势? 当x取何值 时,y=0?
当x取何值时,y>0?
当0
(1)当m取何值时,y随x的增大而增大?
这时它的图象经过哪些象限?
(2)当 m取何值时,y随x的增大而减小?
这时它的图象经过哪些象限?1.已知函数y=(m-3)x-2/3. (1)?当m取何值时,y随x的增大而增大? (2) 当m取何值时,y随x的增大而减小? 课堂练习:例 题例2、对于一次函数y=(a+4)x+2a-1,如果
y随x的增大而增大,且它的图象与y轴的
交点在x轴的下方,试求a的取值范围拓展与应用1.一次函数y=kx+b中,kb>0,且y随x的增大而
减小,则它的图象大致为( )2:已知一次函数y=(1-2m)x+m-1,若函数y随x的增大而减小,并且函数的图象经过二、三、四象限,求m的取值范围.3:已知一次函数y=(3m-8)x+1-m图象与y轴交点在x轴下方,且y随x的增大而减小,其中m为整数. (1)求m的值;(2)当x取何值时,0<y<4?一次函数中k与b的正、负与它的图象经过的象限归纳列表为: 试一试 (2)、(4) 创设情境一次函数的图象是一条直线,一般情况下我们画一次函数的图象,取哪两个点比较简便? (0,b)(-b/k,0)和再见!
