2017_2018学年七年级数学下册10.2直方图课时提升作业(解析版)(新版)新人教版
文档属性
| 名称 | 2017_2018学年七年级数学下册10.2直方图课时提升作业(解析版)(新版)新人教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 323.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-19 20:37:03 | ||
图片预览


文档简介
直 方 图
(30分钟 50分)
一、选择题(每小题4分,共12分)
1.自来水公司为了解居民某月用水的情况,随机抽取了20户居民的月用水量x(单位:立方米),绘制出表格,则月用水量x<3的频率是( )
月用水量
频数
0≤x<0.5
1
0.5≤x<1
2
1≤x<1.5
3
1.5≤x<2
4
2≤x<2.5
3
2.5≤x<3
3
3≤x<3.5
2
3.5≤x<4
1
4≤x<4.5
1
A.0.15 B.0.3 C.0.8 D.0.9
【解析】选C.由图可得,月用水量x<3的总户数为:1+2+3+4+3+3=16,则频率==0.8.
【变式训练】某棉纺厂为了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如下表所示,则棉花纤维长度的数据在16≤x<32这个范围的频率为( )
棉花纤维长度x
频数
0≤x<8
1
8≤x<16
2
16≤x<24
8
24≤x<32
6
32≤x<40
3
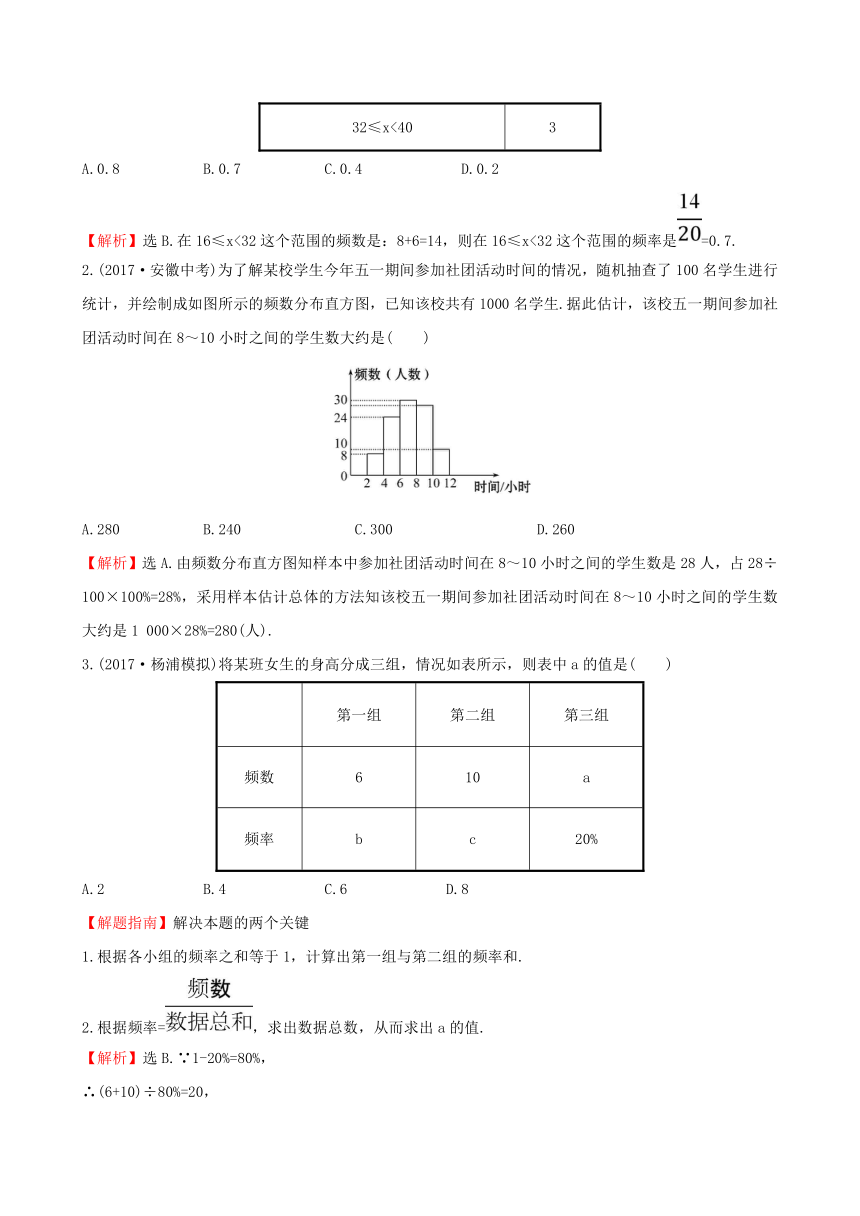
A.0.8 B.0.7 C.0.4 D.0.2
【解析】选B.在16≤x<32这个范围的频数是:8+6=14,则在16≤x<32这个范围的频率是=0.7.
2.(2017·安徽中考)为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了100名学生进行统计,并绘制成如图所示的频数分布直方图,已知该校共有1000名学生.据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )
A.280 B.240 C.300 D.260
【解析】选A.由频数分布直方图知样本中参加社团活动时间在8~10小时之间的学生数是28人,占28÷100×100%=28%,采用样本估计总体的方法知该校五一期间参加社团活动时间在8~10小时之间的学生数大约是1 000×28%=280(人).
3.(2017·杨浦模拟)将某班女生的身高分成三组,情况如表所示,则表中a的值是( )
第一组
第二组
第三组
频数
6
10
a
频率
b
c
20%
A.2 B.4 C.6 D.8
【解题指南】解决本题的两个关键
1.根据各小组的频率之和等于1,计算出第一组与第二组的频率和.
2.根据频率=,求出数据总数,从而求出a的值.
【解析】选B.∵1-20%=80%,
∴(6+10)÷80%=20,
∴20×20%=4.即a=4.
二、填空题(每小题4分,共12分)
4.某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表.已知该校全体学生人数为1200人,由此可以估计每周课外阅读时间在1~2(不含1)小时的学生有________人.
每周课外阅读
时间(小时)
0~1
1~2
(不含1)
2~3
(不含2)
超过3
人数
7
10
14
19
【解析】根据表格中的数据可计算出抽查了50名学生,每周课外阅读时间在1~2(不含1)小时的学生有10人,占20%,
所以该校每周课外阅读时间在1~2(不含1)小时的学生大约有1200×20%=240(人).
答案:240
5.为了支援地震灾区同学,某校开展捐书活动,九(1)班同学积极参与,现将捐书数量绘制成频数分布直方图(如图所示),如果捐书数量在3.5~4.5组别的频率是0.3,那么捐书数量在4.5~5.5组别的人数是________.
【解析】∵捐书数量在3.5~4.5组别的频数是12、频率是0.3,∴捐书的总人数为12÷0.3=40(人),
∴捐书数量在4.5~5.5组别的人数是40-(4+12+8)=16.
答案:16
6.有一个样本,样本容量为80.根据这个样本绘制出频数分布直方图,图中四个小组所对应的四个小长方形的高之比为2∶3∶4∶1,那么第二小组的频数是______.
【解析】∵四个小组所对应的四个小长方形的高之比为2∶3∶4∶1,
∴设四个小组的频数分别为2x,3x,4x,x,
根据样本容量为80可得:
2x+3x+4x+x=80,
解得:x=8,
∴第二小组的频数为3x=24.
答案:24
三、解答题(共26分)
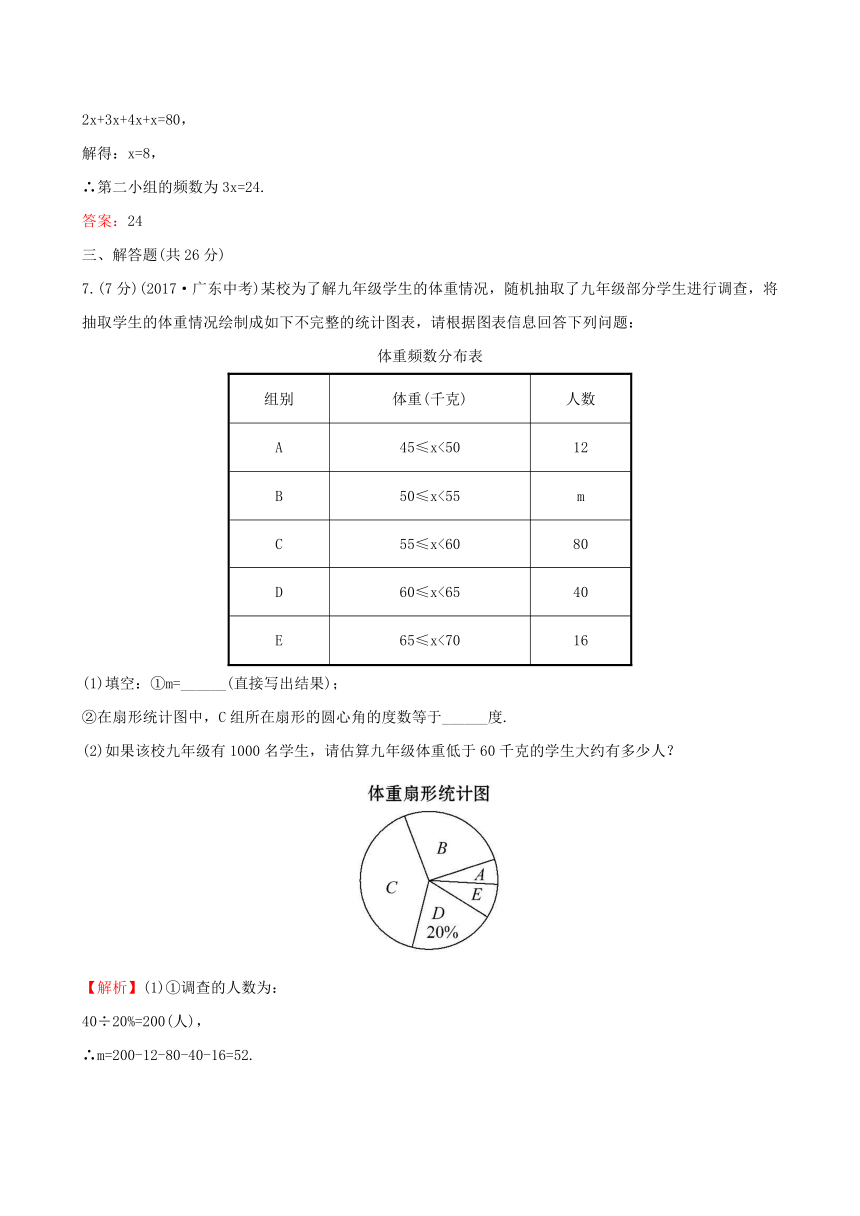
7.(7分)(2017·广东中考)某校为了解九年级学生的体重情况,随机抽取了九年级部分学生进行调查,将抽取学生的体重情况绘制成如下不完整的统计图表,请根据图表信息回答下列问题:
体重频数分布表
组别
体重(千克)
人数
A
45≤x<50
12
B
50≤x<55
m
C
55≤x<60
80
D
60≤x<65
40
E
65≤x<70
16
(1)填空:①m=______(直接写出结果);
②在扇形统计图中,C组所在扇形的圆心角的度数等于______度.
(2)如果该校九年级有1000名学生,请估算九年级体重低于60千克的学生大约有多少人?
【解析】(1)①调查的人数为:
40÷20%=200(人),
∴m=200-12-80-40-16=52.
②C组所在扇形的圆心角的度数为×360°=144°.
答案:①52 ②144
(2)九年级体重低于60千克的学生大约有
×1000=720(人).
8.(9分)(2017·杭州中考)为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数分布表和未完成的频数分布直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数分布表
组别(m)
频数
1.09~1.19
8
1.19~1.29
12
1.29~1.39
a
1.39~1.49
10
(1)求a的值,并把频数分布直方图补充完整.
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.
【解析】(1)a=50-8-12-10=20,
补全频数分布直方图如图所示:
(2)该年级学生跳高成绩在1.29m(含1.29m)以上的人数是:500×=300(人).
【培优训练】
9.(10分)某区在实施居民用水定额管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨),并将调查数据进行了如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3
4.8 6.7 4.5 5.1 6.5 8.9 2.2 4.5
3.2 3.2 4.5 3.5 3.5 3.5 3.6 4.9
3.7 3.8 5.6 5.5 5.9 6.2 5.7 3.9
4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5
6.2 7.5
频数分布表
分组
划记
频数
2.0正正
11
3.5正正正
19
5.06.58.02
合计
50
(1)把上面的频数分布表和频数分布直方图补充完整.
(2)从直方图中你能得到什么信息?(写出两条即可)
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
【解析】(1)
分组
划记
频数
2.03.55.0正正
13
6.5正
5
8.0合计
(2)答案不唯一:如①从直方图可以看出:居民月均用水量大部分在2.0至6.5之间;②居民月均用水量在3.5(3)要使60%的家庭收费不受影响,家庭月均用水量应该定为5吨,因为月均用水量不超过5吨的有30户,×100%?60%.
(30分钟 50分)
一、选择题(每小题4分,共12分)
1.自来水公司为了解居民某月用水的情况,随机抽取了20户居民的月用水量x(单位:立方米),绘制出表格,则月用水量x<3的频率是( )
月用水量
频数
0≤x<0.5
1
0.5≤x<1
2
1≤x<1.5
3
1.5≤x<2
4
2≤x<2.5
3
2.5≤x<3
3
3≤x<3.5
2
3.5≤x<4
1
4≤x<4.5
1
A.0.15 B.0.3 C.0.8 D.0.9
【解析】选C.由图可得,月用水量x<3的总户数为:1+2+3+4+3+3=16,则频率==0.8.
【变式训练】某棉纺厂为了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如下表所示,则棉花纤维长度的数据在16≤x<32这个范围的频率为( )
棉花纤维长度x
频数
0≤x<8
1
8≤x<16
2
16≤x<24
8
24≤x<32
6
32≤x<40
3
A.0.8 B.0.7 C.0.4 D.0.2
【解析】选B.在16≤x<32这个范围的频数是:8+6=14,则在16≤x<32这个范围的频率是=0.7.
2.(2017·安徽中考)为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了100名学生进行统计,并绘制成如图所示的频数分布直方图,已知该校共有1000名学生.据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )
A.280 B.240 C.300 D.260
【解析】选A.由频数分布直方图知样本中参加社团活动时间在8~10小时之间的学生数是28人,占28÷100×100%=28%,采用样本估计总体的方法知该校五一期间参加社团活动时间在8~10小时之间的学生数大约是1 000×28%=280(人).
3.(2017·杨浦模拟)将某班女生的身高分成三组,情况如表所示,则表中a的值是( )
第一组
第二组
第三组
频数
6
10
a
频率
b
c
20%
A.2 B.4 C.6 D.8
【解题指南】解决本题的两个关键
1.根据各小组的频率之和等于1,计算出第一组与第二组的频率和.
2.根据频率=,求出数据总数,从而求出a的值.
【解析】选B.∵1-20%=80%,
∴(6+10)÷80%=20,
∴20×20%=4.即a=4.
二、填空题(每小题4分,共12分)
4.某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表.已知该校全体学生人数为1200人,由此可以估计每周课外阅读时间在1~2(不含1)小时的学生有________人.
每周课外阅读
时间(小时)
0~1
1~2
(不含1)
2~3
(不含2)
超过3
人数
7
10
14
19
【解析】根据表格中的数据可计算出抽查了50名学生,每周课外阅读时间在1~2(不含1)小时的学生有10人,占20%,
所以该校每周课外阅读时间在1~2(不含1)小时的学生大约有1200×20%=240(人).
答案:240
5.为了支援地震灾区同学,某校开展捐书活动,九(1)班同学积极参与,现将捐书数量绘制成频数分布直方图(如图所示),如果捐书数量在3.5~4.5组别的频率是0.3,那么捐书数量在4.5~5.5组别的人数是________.
【解析】∵捐书数量在3.5~4.5组别的频数是12、频率是0.3,∴捐书的总人数为12÷0.3=40(人),
∴捐书数量在4.5~5.5组别的人数是40-(4+12+8)=16.
答案:16
6.有一个样本,样本容量为80.根据这个样本绘制出频数分布直方图,图中四个小组所对应的四个小长方形的高之比为2∶3∶4∶1,那么第二小组的频数是______.
【解析】∵四个小组所对应的四个小长方形的高之比为2∶3∶4∶1,
∴设四个小组的频数分别为2x,3x,4x,x,
根据样本容量为80可得:
2x+3x+4x+x=80,
解得:x=8,
∴第二小组的频数为3x=24.
答案:24
三、解答题(共26分)
7.(7分)(2017·广东中考)某校为了解九年级学生的体重情况,随机抽取了九年级部分学生进行调查,将抽取学生的体重情况绘制成如下不完整的统计图表,请根据图表信息回答下列问题:
体重频数分布表
组别
体重(千克)
人数
A
45≤x<50
12
B
50≤x<55
m
C
55≤x<60
80
D
60≤x<65
40
E
65≤x<70
16
(1)填空:①m=______(直接写出结果);
②在扇形统计图中,C组所在扇形的圆心角的度数等于______度.
(2)如果该校九年级有1000名学生,请估算九年级体重低于60千克的学生大约有多少人?
【解析】(1)①调查的人数为:
40÷20%=200(人),
∴m=200-12-80-40-16=52.
②C组所在扇形的圆心角的度数为×360°=144°.
答案:①52 ②144
(2)九年级体重低于60千克的学生大约有
×1000=720(人).
8.(9分)(2017·杭州中考)为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数分布表和未完成的频数分布直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数分布表
组别(m)
频数
1.09~1.19
8
1.19~1.29
12
1.29~1.39
a
1.39~1.49
10
(1)求a的值,并把频数分布直方图补充完整.
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.
【解析】(1)a=50-8-12-10=20,
补全频数分布直方图如图所示:
(2)该年级学生跳高成绩在1.29m(含1.29m)以上的人数是:500×=300(人).
【培优训练】
9.(10分)某区在实施居民用水定额管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨),并将调查数据进行了如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3
4.8 6.7 4.5 5.1 6.5 8.9 2.2 4.5
3.2 3.2 4.5 3.5 3.5 3.5 3.6 4.9
3.7 3.8 5.6 5.5 5.9 6.2 5.7 3.9
4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5
6.2 7.5
频数分布表
分组
划记
频数
2.0
11
3.5
19
5.0
合计
50
(1)把上面的频数分布表和频数分布直方图补充完整.
(2)从直方图中你能得到什么信息?(写出两条即可)
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
【解析】(1)
分组
划记
频数
2.0
13
6.5
5
8.0
(2)答案不唯一:如①从直方图可以看出:居民月均用水量大部分在2.0至6.5之间;②居民月均用水量在3.5
