2017-2018学年七年级数学下册第九章不等式与不等式组9.3一元一次不等式组课时提升作业(含解析)(新版)新人教版(1)
文档属性
| 名称 | 2017-2018学年七年级数学下册第九章不等式与不等式组9.3一元一次不等式组课时提升作业(含解析)(新版)新人教版(1) |
|
|
| 格式 | zip | ||
| 文件大小 | 245.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-20 00:00:00 | ||
图片预览


文档简介
一元一次不等式组
(30分钟 50分)
一、选择题(每小题3分,共9分)
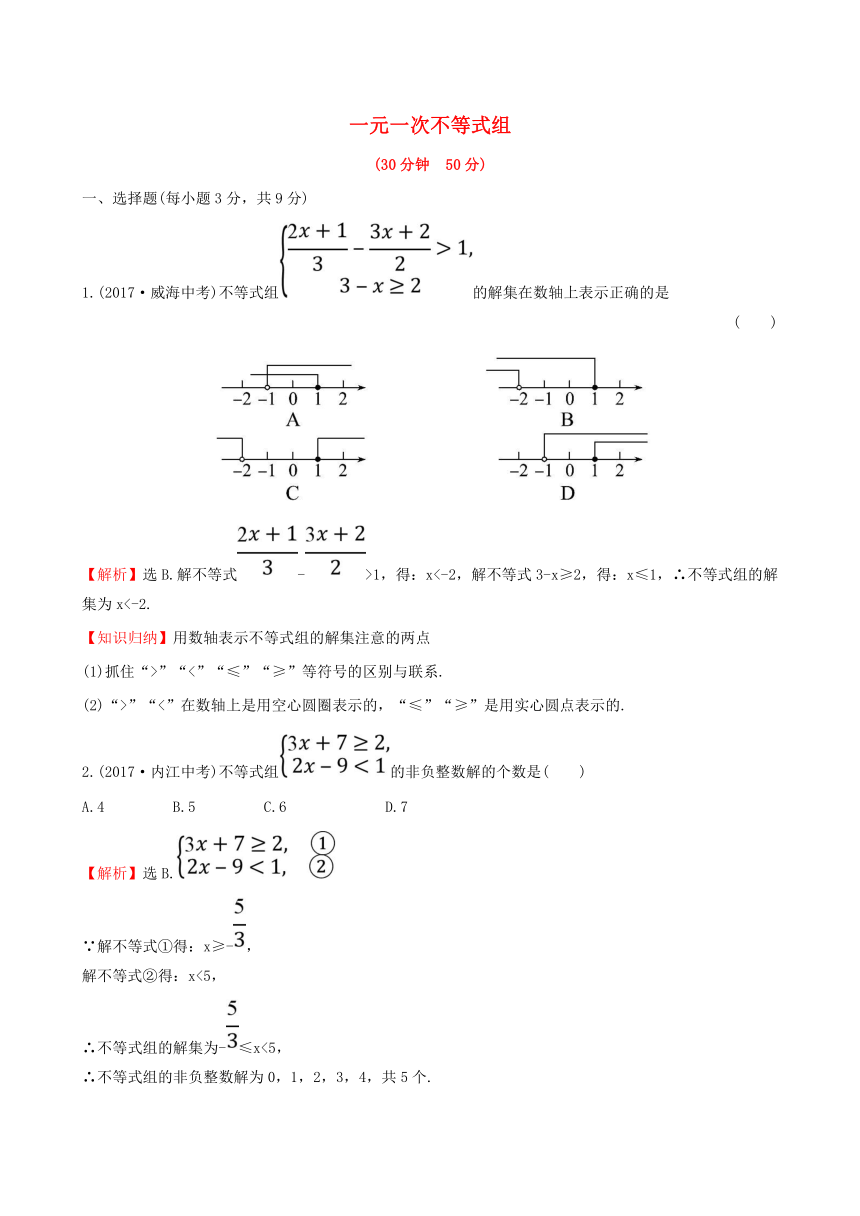
1.(2017·威海中考)不等式组的解集在数轴上表示正确的是
( )
【解析】选B.解不等式->1,得:x<-2,解不等式3-x≥2,得:x≤1,∴不等式组的解集为x<-2.
【知识归纳】用数轴表示不等式组的解集注意的两点
(1)抓住“>”“<”“≤”“≥”等符号的区别与联系.
(2)“>”“<”在数轴上是用空心圆圈表示的,“≤”“≥”是用实心圆点表示的.
2.(2017·内江中考)不等式组的非负整数解的个数是( )
A.4 B.5 C.6 D.7
【解析】选B.
∵解不等式①得:x≥-,
解不等式②得:x<5,
∴不等式组的解集为-≤x<5,
∴不等式组的非负整数解为0,1,2,3,4,共5个.
3.(2017·泰安中考)不等式组的解集为x<2,则k的取值范围为( )
A.k>1 B.k<1
C.k≥1 D.k≤1
【解析】选C.解不等式组
得
∵不等式组的解集为x<2,
∴k+1≥2,解得k≥1.
【变式训练】(2017·金华中考)若关于x的一元一次不等式组
的解是x<5,则m的取值范围是( )
A.m≥5 B.m>5 C.m≤5 D.m<5
【解析】选A.解不等式2x-1>3(x-2),得:x<5,∵不等式组的解集为x<5,
∴m≥5.
二、填空题(每小题4分,共12分)
4.若干学生分住宿舍,每间住4人余20人;每间住8人有一间不空也不满,则学生有________人.
【解析】设宿舍有x间,则
解得5则x=6.
学生有4×6+20=44(人).
答案:44
5.(2017·黑龙江中考)若关于x的一元一次不等式组无解,则a的取值范围是________.
【解析】由x-a>0得,x>a;
由1-x>x-1得,x<1,
∵此不等式组的解集是空集,
∴a≥1.
答案:a≥1
6.(2017·宜宾中考)若关于x,y的二元一次方程组的解满足x+y>0,则m的取值范围是________.
【解析】
②-①得4y=2-2m,则y=,
把y=代入②得x=3-=,
则x+y>0即+>0,解得m>-2.
答案:m>-2
三、解答题(共29分)
7.(10分)(1)(2017·北京中考)解不等式组:
【解析】
由①式得x<3;
由②式得x<2,
所以不等式组的解集为x<2.
(2)(2017·长沙中考)解不等式组并把它的解集在数轴上表示出来.
【解析】解不等式2x≥-9-x,得:x≥-3,
解不等式5x-1>3(x+1),得:x>2,
则不等式组的解集为x>2,
将解集表示在数轴上如下:
8.(8分)小明利用课余时间回收废品,将卖得的钱去购买5本大小不同的两种笔记本,要求共花钱不超过28元,且购买的笔记本的总页数不低于340页,两种笔记本的价格和页数如表.
大笔记本
小笔记本
价格(元/本)
6
5
页数(页/本)
100
60
为了节约资金,小明应选择哪一种购买方案?请说明理由.
【解析】设购买大笔记本为x本,则购买小笔记本为(5-x)本,
依题意,得
解得1≤x≤3.
x为整数,∴x的取值为1,2,3;
当x =1时,购买笔记本的总金额为6×1+5×4=26(元);
当x =2时,购买笔记本的总金额为6×2+5×3=27(元);
当x =3时,购买笔记本的总金额为6×3+5×2=28(元).
∴应购买大笔记本1本,小笔记本4本,花钱最少.
【规律总结】应用一元一次不等式组解实际问题的步骤:
(1)分析题意,找出不等关系.
(2)设未知数,列出不等式组.
(3)解不等式组.
(4)从不等式组解集中找出符合题意的答案.
(5)作答.
【培优训练】
9.(11分)(2017·资阳中考)四川省安岳县盛产柠檬和柚子两种水果.今年,某公司计划用同种型号的汽车运输柠檬和柚子到外地销售,运输中要求每辆汽车都要满载装运,且只能装运一种水果.若用3辆汽车装载柠檬、2辆汽车装载柚子共可装载33吨;若用2辆汽车装载柠檬、3辆汽车装载柚子共可装载32吨.
(1)求每辆汽车可装载柠檬或柚子各多少吨?
(2)据调查,全部销售完后,每吨柠檬可获利700元、每吨柚子可获利500元,计划用20辆汽车运输,且柚子不少于30吨,如何安排运输才能使公司获利最大,最大利润是多少元?
【解析】(1)设每辆汽车可装载柠檬m吨,装载柚子n吨,根据题意,得
解得
答:每辆汽车可装载柠檬7吨,或装载柚子6吨.
(2)设用x辆汽车装载柚子,则用(20-x)辆汽车装载柠檬,总利润为y元.
根据题意,得6x≥30,即x≥5.
y=500×6x+700×7(20-x)=-1900x+98000.
∵y随x的增大而减小.
∴当x=5时,y取得最大值,最大值=-1900×5+98000=88500(元).
答:安排5辆汽车运输柚子,15辆汽车运输柠檬可使公司利润最大,最大利润为88500元.
(30分钟 50分)
一、选择题(每小题3分,共9分)
1.(2017·威海中考)不等式组的解集在数轴上表示正确的是
( )
【解析】选B.解不等式->1,得:x<-2,解不等式3-x≥2,得:x≤1,∴不等式组的解集为x<-2.
【知识归纳】用数轴表示不等式组的解集注意的两点
(1)抓住“>”“<”“≤”“≥”等符号的区别与联系.
(2)“>”“<”在数轴上是用空心圆圈表示的,“≤”“≥”是用实心圆点表示的.
2.(2017·内江中考)不等式组的非负整数解的个数是( )
A.4 B.5 C.6 D.7
【解析】选B.
∵解不等式①得:x≥-,
解不等式②得:x<5,
∴不等式组的解集为-≤x<5,
∴不等式组的非负整数解为0,1,2,3,4,共5个.
3.(2017·泰安中考)不等式组的解集为x<2,则k的取值范围为( )
A.k>1 B.k<1
C.k≥1 D.k≤1
【解析】选C.解不等式组
得
∵不等式组的解集为x<2,
∴k+1≥2,解得k≥1.
【变式训练】(2017·金华中考)若关于x的一元一次不等式组
的解是x<5,则m的取值范围是( )
A.m≥5 B.m>5 C.m≤5 D.m<5
【解析】选A.解不等式2x-1>3(x-2),得:x<5,∵不等式组的解集为x<5,
∴m≥5.
二、填空题(每小题4分,共12分)
4.若干学生分住宿舍,每间住4人余20人;每间住8人有一间不空也不满,则学生有________人.
【解析】设宿舍有x间,则
解得5
学生有4×6+20=44(人).
答案:44
5.(2017·黑龙江中考)若关于x的一元一次不等式组无解,则a的取值范围是________.
【解析】由x-a>0得,x>a;
由1-x>x-1得,x<1,
∵此不等式组的解集是空集,
∴a≥1.
答案:a≥1
6.(2017·宜宾中考)若关于x,y的二元一次方程组的解满足x+y>0,则m的取值范围是________.
【解析】
②-①得4y=2-2m,则y=,
把y=代入②得x=3-=,
则x+y>0即+>0,解得m>-2.
答案:m>-2
三、解答题(共29分)
7.(10分)(1)(2017·北京中考)解不等式组:
【解析】
由①式得x<3;
由②式得x<2,
所以不等式组的解集为x<2.
(2)(2017·长沙中考)解不等式组并把它的解集在数轴上表示出来.
【解析】解不等式2x≥-9-x,得:x≥-3,
解不等式5x-1>3(x+1),得:x>2,
则不等式组的解集为x>2,
将解集表示在数轴上如下:
8.(8分)小明利用课余时间回收废品,将卖得的钱去购买5本大小不同的两种笔记本,要求共花钱不超过28元,且购买的笔记本的总页数不低于340页,两种笔记本的价格和页数如表.
大笔记本
小笔记本
价格(元/本)
6
5
页数(页/本)
100
60
为了节约资金,小明应选择哪一种购买方案?请说明理由.
【解析】设购买大笔记本为x本,则购买小笔记本为(5-x)本,
依题意,得
解得1≤x≤3.
x为整数,∴x的取值为1,2,3;
当x =1时,购买笔记本的总金额为6×1+5×4=26(元);
当x =2时,购买笔记本的总金额为6×2+5×3=27(元);
当x =3时,购买笔记本的总金额为6×3+5×2=28(元).
∴应购买大笔记本1本,小笔记本4本,花钱最少.
【规律总结】应用一元一次不等式组解实际问题的步骤:
(1)分析题意,找出不等关系.
(2)设未知数,列出不等式组.
(3)解不等式组.
(4)从不等式组解集中找出符合题意的答案.
(5)作答.
【培优训练】
9.(11分)(2017·资阳中考)四川省安岳县盛产柠檬和柚子两种水果.今年,某公司计划用同种型号的汽车运输柠檬和柚子到外地销售,运输中要求每辆汽车都要满载装运,且只能装运一种水果.若用3辆汽车装载柠檬、2辆汽车装载柚子共可装载33吨;若用2辆汽车装载柠檬、3辆汽车装载柚子共可装载32吨.
(1)求每辆汽车可装载柠檬或柚子各多少吨?
(2)据调查,全部销售完后,每吨柠檬可获利700元、每吨柚子可获利500元,计划用20辆汽车运输,且柚子不少于30吨,如何安排运输才能使公司获利最大,最大利润是多少元?
【解析】(1)设每辆汽车可装载柠檬m吨,装载柚子n吨,根据题意,得
解得
答:每辆汽车可装载柠檬7吨,或装载柚子6吨.
(2)设用x辆汽车装载柚子,则用(20-x)辆汽车装载柠檬,总利润为y元.
根据题意,得6x≥30,即x≥5.
y=500×6x+700×7(20-x)=-1900x+98000.
∵y随x的增大而减小.
∴当x=5时,y取得最大值,最大值=-1900×5+98000=88500(元).
答:安排5辆汽车运输柚子,15辆汽车运输柠檬可使公司利润最大,最大利润为88500元.
