2017-2018学年七年级数学下册第五章相交线与平行线5.2平行线及其判定5.2.1平行线一课一练基础闯关(含解析)(新版)新人教版
文档属性
| 名称 | 2017-2018学年七年级数学下册第五章相交线与平行线5.2平行线及其判定5.2.1平行线一课一练基础闯关(含解析)(新版)新人教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 245.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-20 12:54:41 | ||
图片预览

文档简介
平行线
一课一练·基础闯关
题组平行线及其画法
1.下列说法正确的是 ( )
A.在同一平面内,不重合的两条直线不相交就平行
B.两条直线的位置关系有三种:相交、垂直、平行
C.过两条直线a,b外一点P,画直线c,使c∥a,且c∥b
D.过直线AB外一点P画AB的平行线,可以画无数条
【解析】选A,垂直是相交的特例,故B错;若a和b相交,则过点P不存在一条直线使它与两条相交直线同时平行;过直线外一点,有且只有一条直线与已知直线平行.
【易错提醒】垂直也是相交的一种,不要把其单列为一种情况.
2.(2017·钦州月考)下列说法正确的是( )
A.不相交的两条线段是平行线
B.不相交的两条直线是平行线
C.不相交的两条射线是平行线
D.在同一平面内,不相交的两条直线是平行线
【解析】选D.根据平行线的定义:在同一平面内,不相交的两条直线是平行线.A,B,C错误;D正确.
【易错警示】平行线定义的理解
抓住三个关键要素:“同一平面内”“不相交”“直线”,本题易错之处在于理解平行线定义时,容易只关注其中一个或两个条件而导致判断错误.
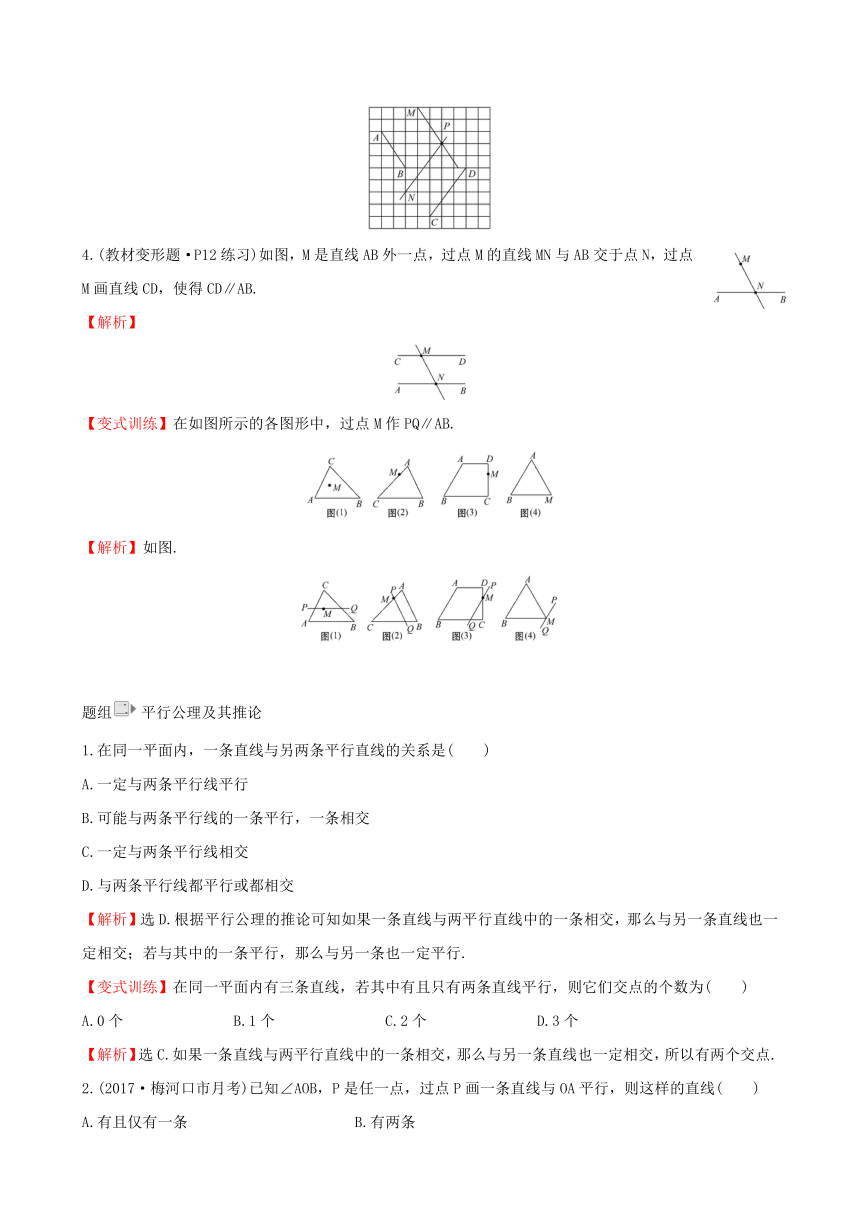
3.在图中的方格纸中过点P分别画出PM∥AB和PN∥CD.
【解析】如图:
4.(教材变形题·P12练习)如图,M是直线AB外一点,过点M的直线MN与AB交于点N,过点M画直线CD,使得CD∥AB.
【解析】
【变式训练】在如图所示的各图形中,过点M作PQ∥AB.
【解析】如图.
题组平行公理及其推论
1.在同一平面内,一条直线与另两条平行直线的关系是( )
A.一定与两条平行线平行
B.可能与两条平行线的一条平行,一条相交
C.一定与两条平行线相交
D.与两条平行线都平行或都相交
【解析】选D.根据平行公理的推论可知如果一条直线与两平行直线中的一条相交,那么与另一条直线也一定相交;若与其中的一条平行,那么与另一条也一定平行.
【变式训练】在同一平面内有三条直线,若其中有且只有两条直线平行,则它们交点的个数为( )
A.0个 B.1个 C.2个 D.3个
【解析】选C.如果一条直线与两平行直线中的一条相交,那么与另一条直线也一定相交,所以有两个交点.
2.(2017·梅河口市月考)已知∠AOB,P是任一点,过点P画一条直线与OA平行,则这样的直线( )
A.有且仅有一条 B.有两条
C.不存在 D.有一条或不存在
【解析】选D.①若点P在OA上,则不能画出与OA平行的直线;②若点P不在OA上,则过点P有且只有一条直线与OA平行,所以这样的直线有一条或不存在.
3.如图,PC∥AB,QC∥AB,则点P,C,Q在一条直线上.
理由是:_______________________________________________________.
【解析】因为经过直线外一点有且只有一条直线与已知直线平行,所以,P,C,Q三点在同一条直线上.
答案:经过直线外一点有且只有一条直线与已知直线平行
4.将一张长方形的硬纸片ABCD对折后打开,折痕为EF,把长方形ABEF平摊在桌面上,另一面CDFE无论怎样改变位置,总有CD∥AB存在,为什么?
【解析】因为CD∥EF,EF∥AB,所以CD∥AB.
在同一平面内三条直线交点有多少个?
甲:同一平面三直线相交交点的个数为0个,因为a∥b∥c,如图(1)所示.
乙:同一平面内三条直线交点个数只有1个,因为a,b,c交于同一点O,如图(2)所示.
以上说法谁对谁错?为什么?
【解析】甲,乙说法都不对,各自少了三种情况.a∥b,c与a,b相交如图(1),a,b,c两两相交如图(2),所以三条直线互不重合,交点有0个或1个或2个或3个,共四种情况.
【母题变式】(2017·钦州月考)平面内有10条直线,无任何三条交于一点,欲使它们有31个交点,怎样才能办到.
【解析】使5条直线平行,另3条直线平行且都与这5条相交,再有2条直线平行且都与这5条相交,且3条和2条也有相交.
如图所示:
一课一练·基础闯关
题组平行线及其画法
1.下列说法正确的是 ( )
A.在同一平面内,不重合的两条直线不相交就平行
B.两条直线的位置关系有三种:相交、垂直、平行
C.过两条直线a,b外一点P,画直线c,使c∥a,且c∥b
D.过直线AB外一点P画AB的平行线,可以画无数条
【解析】选A,垂直是相交的特例,故B错;若a和b相交,则过点P不存在一条直线使它与两条相交直线同时平行;过直线外一点,有且只有一条直线与已知直线平行.
【易错提醒】垂直也是相交的一种,不要把其单列为一种情况.
2.(2017·钦州月考)下列说法正确的是( )
A.不相交的两条线段是平行线
B.不相交的两条直线是平行线
C.不相交的两条射线是平行线
D.在同一平面内,不相交的两条直线是平行线
【解析】选D.根据平行线的定义:在同一平面内,不相交的两条直线是平行线.A,B,C错误;D正确.
【易错警示】平行线定义的理解
抓住三个关键要素:“同一平面内”“不相交”“直线”,本题易错之处在于理解平行线定义时,容易只关注其中一个或两个条件而导致判断错误.
3.在图中的方格纸中过点P分别画出PM∥AB和PN∥CD.
【解析】如图:
4.(教材变形题·P12练习)如图,M是直线AB外一点,过点M的直线MN与AB交于点N,过点M画直线CD,使得CD∥AB.
【解析】
【变式训练】在如图所示的各图形中,过点M作PQ∥AB.
【解析】如图.
题组平行公理及其推论
1.在同一平面内,一条直线与另两条平行直线的关系是( )
A.一定与两条平行线平行
B.可能与两条平行线的一条平行,一条相交
C.一定与两条平行线相交
D.与两条平行线都平行或都相交
【解析】选D.根据平行公理的推论可知如果一条直线与两平行直线中的一条相交,那么与另一条直线也一定相交;若与其中的一条平行,那么与另一条也一定平行.
【变式训练】在同一平面内有三条直线,若其中有且只有两条直线平行,则它们交点的个数为( )
A.0个 B.1个 C.2个 D.3个
【解析】选C.如果一条直线与两平行直线中的一条相交,那么与另一条直线也一定相交,所以有两个交点.
2.(2017·梅河口市月考)已知∠AOB,P是任一点,过点P画一条直线与OA平行,则这样的直线( )
A.有且仅有一条 B.有两条
C.不存在 D.有一条或不存在
【解析】选D.①若点P在OA上,则不能画出与OA平行的直线;②若点P不在OA上,则过点P有且只有一条直线与OA平行,所以这样的直线有一条或不存在.
3.如图,PC∥AB,QC∥AB,则点P,C,Q在一条直线上.
理由是:_______________________________________________________.
【解析】因为经过直线外一点有且只有一条直线与已知直线平行,所以,P,C,Q三点在同一条直线上.
答案:经过直线外一点有且只有一条直线与已知直线平行
4.将一张长方形的硬纸片ABCD对折后打开,折痕为EF,把长方形ABEF平摊在桌面上,另一面CDFE无论怎样改变位置,总有CD∥AB存在,为什么?
【解析】因为CD∥EF,EF∥AB,所以CD∥AB.
在同一平面内三条直线交点有多少个?
甲:同一平面三直线相交交点的个数为0个,因为a∥b∥c,如图(1)所示.
乙:同一平面内三条直线交点个数只有1个,因为a,b,c交于同一点O,如图(2)所示.
以上说法谁对谁错?为什么?
【解析】甲,乙说法都不对,各自少了三种情况.a∥b,c与a,b相交如图(1),a,b,c两两相交如图(2),所以三条直线互不重合,交点有0个或1个或2个或3个,共四种情况.
【母题变式】(2017·钦州月考)平面内有10条直线,无任何三条交于一点,欲使它们有31个交点,怎样才能办到.
【解析】使5条直线平行,另3条直线平行且都与这5条相交,再有2条直线平行且都与这5条相交,且3条和2条也有相交.
如图所示:
