2017-2018学年七年级数学下册第五章相交线与平行线5.3平行线的性质5.3.1平行线的性质一课一练基础闯关(含解析)(新版)新人教版
文档属性
| 名称 | 2017-2018学年七年级数学下册第五章相交线与平行线5.3平行线的性质5.3.1平行线的性质一课一练基础闯关(含解析)(新版)新人教版 |
|
|
| 格式 | zip | ||
| 文件大小 | 275.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-20 00:00:00 | ||
图片预览



文档简介
5.3.1 平行线的性质
一课一练·基础闯关
题组平行线的性质
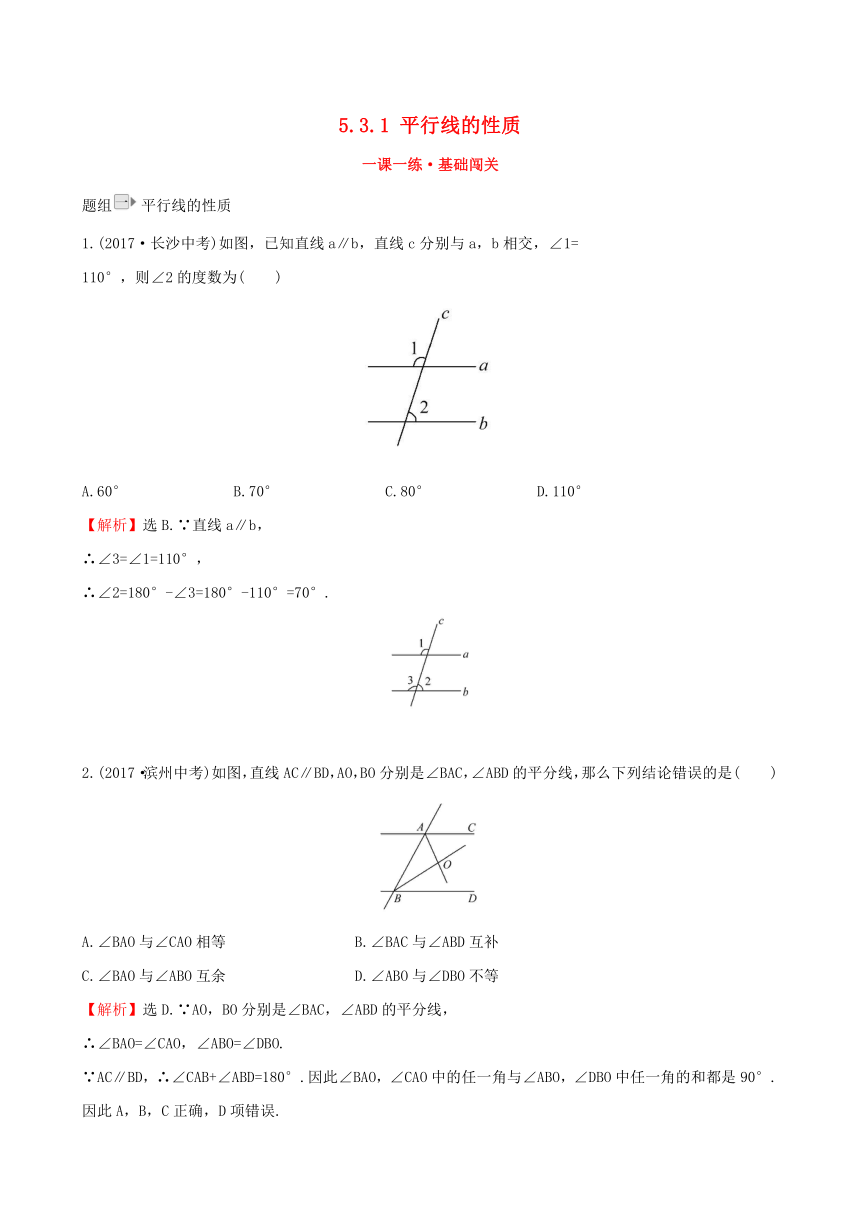
1.(2017·长沙中考)如图,已知直线a∥b,直线c分别与a,b相交,∠1=
110°,则∠2的度数为( )
A.60° B.70° C.80° D.110°
【解析】选B.∵直线a∥b,
∴∠3=∠1=110°,
∴∠2=180°-∠3=180°-110°=70°.
2.(2017·滨州中考)如图,直线AC∥BD,AO,BO分别是∠BAC,∠ABD的平分线,那么下列结论错误的是( )
A.∠BAO与∠CAO相等 B.∠BAC与∠ABD互补
C.∠BAO与∠ABO互余 D.∠ABO与∠DBO不等
【解析】选D.∵AO,BO分别是∠BAC,∠ABD的平分线,
∴∠BAO=∠CAO,∠ABO=∠DBO.
∵AC∥BD,∴∠CAB+∠ABD=180°.因此∠BAO,∠CAO中的任一角与∠ABO,∠DBO中任一角的和都是90°.
因此A,B,C正确,D项错误.
【规律总结】平行线中的一些重要结论
1.两条平行线被第三条直线所截,一对同位角的角平分线互相平行.
2.两条平行线被第三条直线所截,一对内错角的角平分线互相平行.
3.两条平行线被第三条直线所截,一对同旁内角的角平分线互相垂直.
3.(2017·杭州期中)如图,将一条两边互相平行的纸带按图所示折叠,则∠α的度数等于 ( )
A.50° B.60°
C.75° D.85°
【解析】选C.∵AD∥BC,
∴∠2=∠1=30°,
∴2∠α+30°=180°,
∴∠α=75°.
4.(2017·河北一模)如图,m∥n,直角三角板ABC的直角顶点C在两直线之间,两直角边与两直线相交所形成的锐角分别为α,β,则α+β=________.
【解析】过点C作CE∥m,
∵m∥n,
∴CE∥n,
∴∠1=∠α,∠2=∠β.
∵∠1+∠2=90°,
∴α+β=90°.
答案:90°
5.如图,DB∥FG∥EC,∠ACE=36°,AP平分∠BAC,∠PAG=12°,求∠ABD的度数.
【解析】∵FG∥EC,∴∠CAG=∠ACE=36°.
∴∠PAC=∠CAG+∠PAG=36°+12°=48°.
∵AP平分∠BAC,
∴∠BAP=∠PAC=48°.
∵DB∥FG,
∴∠ABD=∠BAG=∠BAP+∠PAG=48°+12°=60°.
题组平行线的性质与判定综合应用
1.(2017·淮安期中)如图,下列结论中不正确的是( )
A.若AD∥BC,则∠1=∠B
B.若∠1=∠2,则AD∥BC
C.若∠2=∠C,则AE∥CD
D.若AE∥CD,则∠1+∠3=180°
【解析】选A.∵AD∥BC,∴∠1=∠2,选项A不正确.
∵∠1=∠2,∴AD∥BC,选项B正确.
∵∠2=∠C,∴AE∥CD,选项C正确.
∵AE∥CD,
∴∠1+∠3=180°,选项D正确.
2.(2017·宿迁中考)如图,直线a,b被直线c,d所截,若∠1=80°,∠2=
100°,∠3=85°,则∠4的度数是( )
A.80° B.85° C.95° D.100°
【解析】选B.∠1+∠2=80°+100°=180°,所以a∥b,根据两直线平行,内错角相等得∠4=85°.
3.(2017·湖州期中)如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2=__________.
【解析】∵c⊥a,c⊥b,∴a∥b.∴∠1=∠2.
∵∠1=50°,∴∠2=50°.
答案:50°
4.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=____°.
【解析】如图,延长AB交l2于点C,
∵l1∥l2,∴∠3=∠1=40°,∵∠α=∠β,∴AC∥ED,
∴∠2=180°-∠3=180°-40°=140°.
答案:140
5.(2017·郯城县月考)如图,∠B=∠ADE,∠DEC=110°,则∠C等于________.
【解析】∵∠B=∠ADE,∴DE∥BC.
∵∠DEC=110°,∴∠C=180°-110°=70°.
答案:70°
6.(2017·岱岳区期中)如图,∠ACE=∠FEC,∠EFB=∠A,试说明FB∥AE.
【解析】∵∠ACE=∠FEC,
∴EF∥AD.
∴∠EFB=∠DBF.
∵∠EFB=∠A,
∴∠DBF=∠A.
∴FB∥AE.
7.如图,C,D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.
(1)CE与DF平行吗?为什么?
(2)若∠DCE=130°,求∠DEF的度数.
【解析】(1)CE∥DF.理由如下:∵∠1+∠2=180°,∠1+∠DCE=180°,
∴∠2=∠DCE,∴CE∥DF.
(2)∵CE∥DF,∠DCE=130°,
∴∠CDF=180°-∠DCE=180°-130°=50°.
∵DE平分∠CDF,
∴∠CDE=∠CDF=25°.
∵EF∥AB,
∴∠DEF=∠CDE=25°.
如图,AB∥CD,分别探索下列四个图形中∠APC与∠PAB,∠PCD之间的关系,请你从所得的四个关系中任选一个加以说明.
【解析】(1)题图(1)中∠APC=360°-∠PAB-∠PCD,
题图(2)中∠APC=∠PAB+∠PCD,
题图(3)中∠APC=∠PCD-∠PAB,
题图(4)中∠APC=180°-∠PAB+∠PCD.
(2)选∠APC=360°-∠PAB-∠PCD加以说明.
如图,过点P作AB的平行线PE.
因为AB∥CD,所以PE∥CD,
所以∠PAB+∠APE=180°,∠PCD+∠CPE=180°,
所以∠PAB+∠PCD+∠APE+∠CPE=360°,
所以∠APC=360°-∠PAB-∠PCD.
【母题变式】如图,AB∥CD,E,F分别是AB,CD之间的两点,且∠BAF=2∠EAF,∠CDF=2∠EDF.
(1)判定∠BAE,∠CDE与∠AED之间的数量关系,并说明理由.
(2)∠AFD与∠AED之间有怎样的数量关系?
【解析】平行线中的拐点问题,通常需过拐点作平行线.
(1)∠AED=∠BAE+∠CDE.理由如下:
如图,过点E作EG∥AB.∵AB∥CD,
∴AB∥EG∥CD,∴∠AEG=∠BAE,∠DEG=∠CDE.
∵∠AED=∠AEG+∠DEG,
∴∠AED=∠BAE+∠CDE.
(2)同(1)可得∠AFD=∠BAF+∠CDF.
∵∠BAF=2∠EAF,∠CDF=2∠EDF,
∴∠BAE+∠CDE=∠BAF+∠CDF=
=∠AFD,
∴∠AED=∠AFD.
一课一练·基础闯关
题组平行线的性质
1.(2017·长沙中考)如图,已知直线a∥b,直线c分别与a,b相交,∠1=
110°,则∠2的度数为( )
A.60° B.70° C.80° D.110°
【解析】选B.∵直线a∥b,
∴∠3=∠1=110°,
∴∠2=180°-∠3=180°-110°=70°.
2.(2017·滨州中考)如图,直线AC∥BD,AO,BO分别是∠BAC,∠ABD的平分线,那么下列结论错误的是( )
A.∠BAO与∠CAO相等 B.∠BAC与∠ABD互补
C.∠BAO与∠ABO互余 D.∠ABO与∠DBO不等
【解析】选D.∵AO,BO分别是∠BAC,∠ABD的平分线,
∴∠BAO=∠CAO,∠ABO=∠DBO.
∵AC∥BD,∴∠CAB+∠ABD=180°.因此∠BAO,∠CAO中的任一角与∠ABO,∠DBO中任一角的和都是90°.
因此A,B,C正确,D项错误.
【规律总结】平行线中的一些重要结论
1.两条平行线被第三条直线所截,一对同位角的角平分线互相平行.
2.两条平行线被第三条直线所截,一对内错角的角平分线互相平行.
3.两条平行线被第三条直线所截,一对同旁内角的角平分线互相垂直.
3.(2017·杭州期中)如图,将一条两边互相平行的纸带按图所示折叠,则∠α的度数等于 ( )
A.50° B.60°
C.75° D.85°
【解析】选C.∵AD∥BC,
∴∠2=∠1=30°,
∴2∠α+30°=180°,
∴∠α=75°.
4.(2017·河北一模)如图,m∥n,直角三角板ABC的直角顶点C在两直线之间,两直角边与两直线相交所形成的锐角分别为α,β,则α+β=________.
【解析】过点C作CE∥m,
∵m∥n,
∴CE∥n,
∴∠1=∠α,∠2=∠β.
∵∠1+∠2=90°,
∴α+β=90°.
答案:90°
5.如图,DB∥FG∥EC,∠ACE=36°,AP平分∠BAC,∠PAG=12°,求∠ABD的度数.
【解析】∵FG∥EC,∴∠CAG=∠ACE=36°.
∴∠PAC=∠CAG+∠PAG=36°+12°=48°.
∵AP平分∠BAC,
∴∠BAP=∠PAC=48°.
∵DB∥FG,
∴∠ABD=∠BAG=∠BAP+∠PAG=48°+12°=60°.
题组平行线的性质与判定综合应用
1.(2017·淮安期中)如图,下列结论中不正确的是( )
A.若AD∥BC,则∠1=∠B
B.若∠1=∠2,则AD∥BC
C.若∠2=∠C,则AE∥CD
D.若AE∥CD,则∠1+∠3=180°
【解析】选A.∵AD∥BC,∴∠1=∠2,选项A不正确.
∵∠1=∠2,∴AD∥BC,选项B正确.
∵∠2=∠C,∴AE∥CD,选项C正确.
∵AE∥CD,
∴∠1+∠3=180°,选项D正确.
2.(2017·宿迁中考)如图,直线a,b被直线c,d所截,若∠1=80°,∠2=
100°,∠3=85°,则∠4的度数是( )
A.80° B.85° C.95° D.100°
【解析】选B.∠1+∠2=80°+100°=180°,所以a∥b,根据两直线平行,内错角相等得∠4=85°.
3.(2017·湖州期中)如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2=__________.
【解析】∵c⊥a,c⊥b,∴a∥b.∴∠1=∠2.
∵∠1=50°,∴∠2=50°.
答案:50°
4.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=____°.
【解析】如图,延长AB交l2于点C,
∵l1∥l2,∴∠3=∠1=40°,∵∠α=∠β,∴AC∥ED,
∴∠2=180°-∠3=180°-40°=140°.
答案:140
5.(2017·郯城县月考)如图,∠B=∠ADE,∠DEC=110°,则∠C等于________.
【解析】∵∠B=∠ADE,∴DE∥BC.
∵∠DEC=110°,∴∠C=180°-110°=70°.
答案:70°
6.(2017·岱岳区期中)如图,∠ACE=∠FEC,∠EFB=∠A,试说明FB∥AE.
【解析】∵∠ACE=∠FEC,
∴EF∥AD.
∴∠EFB=∠DBF.
∵∠EFB=∠A,
∴∠DBF=∠A.
∴FB∥AE.
7.如图,C,D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.
(1)CE与DF平行吗?为什么?
(2)若∠DCE=130°,求∠DEF的度数.
【解析】(1)CE∥DF.理由如下:∵∠1+∠2=180°,∠1+∠DCE=180°,
∴∠2=∠DCE,∴CE∥DF.
(2)∵CE∥DF,∠DCE=130°,
∴∠CDF=180°-∠DCE=180°-130°=50°.
∵DE平分∠CDF,
∴∠CDE=∠CDF=25°.
∵EF∥AB,
∴∠DEF=∠CDE=25°.
如图,AB∥CD,分别探索下列四个图形中∠APC与∠PAB,∠PCD之间的关系,请你从所得的四个关系中任选一个加以说明.
【解析】(1)题图(1)中∠APC=360°-∠PAB-∠PCD,
题图(2)中∠APC=∠PAB+∠PCD,
题图(3)中∠APC=∠PCD-∠PAB,
题图(4)中∠APC=180°-∠PAB+∠PCD.
(2)选∠APC=360°-∠PAB-∠PCD加以说明.
如图,过点P作AB的平行线PE.
因为AB∥CD,所以PE∥CD,
所以∠PAB+∠APE=180°,∠PCD+∠CPE=180°,
所以∠PAB+∠PCD+∠APE+∠CPE=360°,
所以∠APC=360°-∠PAB-∠PCD.
【母题变式】如图,AB∥CD,E,F分别是AB,CD之间的两点,且∠BAF=2∠EAF,∠CDF=2∠EDF.
(1)判定∠BAE,∠CDE与∠AED之间的数量关系,并说明理由.
(2)∠AFD与∠AED之间有怎样的数量关系?
【解析】平行线中的拐点问题,通常需过拐点作平行线.
(1)∠AED=∠BAE+∠CDE.理由如下:
如图,过点E作EG∥AB.∵AB∥CD,
∴AB∥EG∥CD,∴∠AEG=∠BAE,∠DEG=∠CDE.
∵∠AED=∠AEG+∠DEG,
∴∠AED=∠BAE+∠CDE.
(2)同(1)可得∠AFD=∠BAF+∠CDF.
∵∠BAF=2∠EAF,∠CDF=2∠EDF,
∴∠BAE+∠CDE=∠BAF+∠CDF=
=∠AFD,
∴∠AED=∠AFD.
