18.2平行四边形的判定 教学课件 (共24张PPT)
文档属性
| 名称 | 18.2平行四边形的判定 教学课件 (共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 449.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-20 20:25:29 | ||
图片预览


文档简介
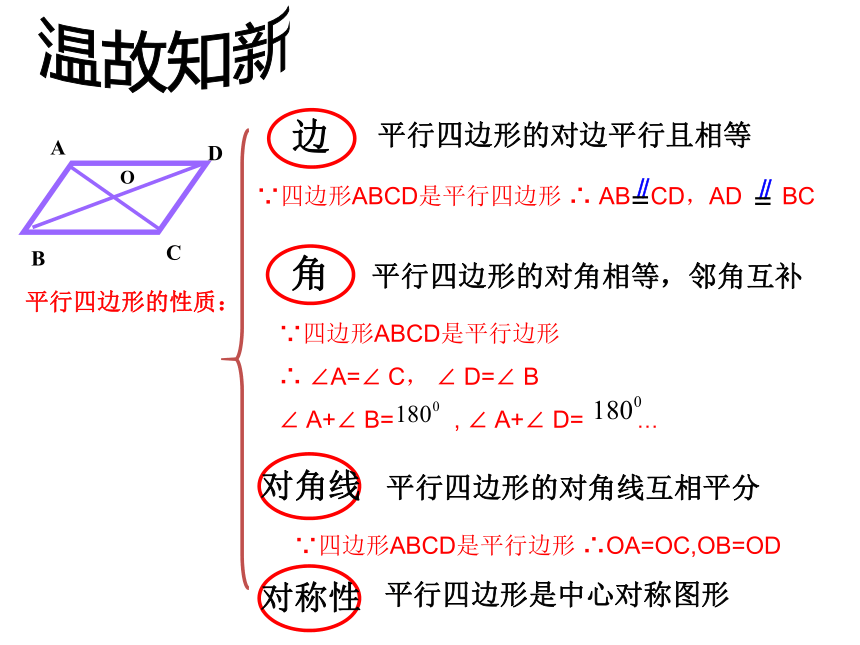
课件24张PPT。18.1.2 平行四边形的判定(1)平行四边形的对边平行且相等 平行四边形的对角线互相平分 温故知新平行四边形的性质:O平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD 平行四边形是中心对称图形平行四边形的定义:
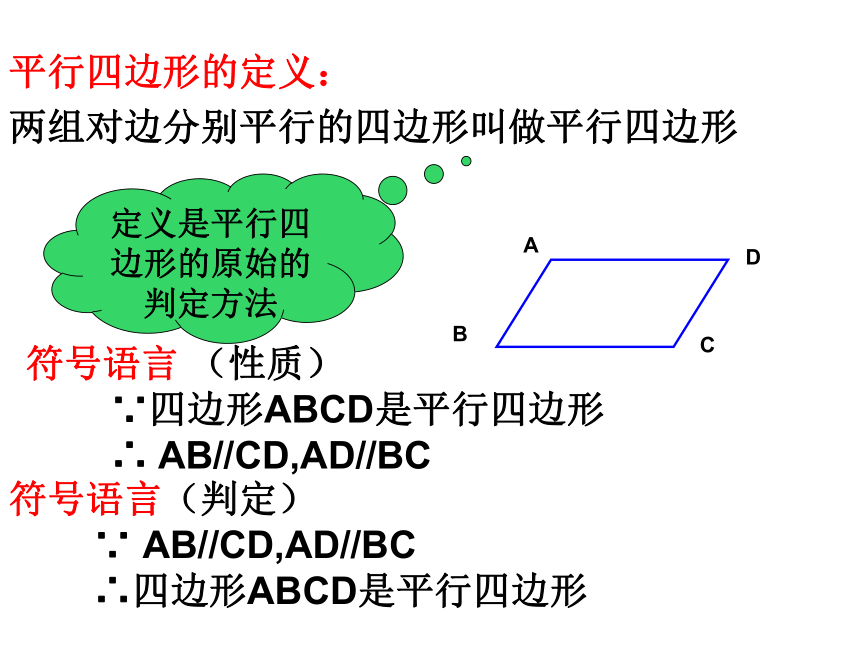
两组对边分别平行的四边形叫做平行四边形
符号语言 (性质)
∵四边形ABCD是平行四边形
∴ AB//CD,AD//BC定义是平行四边形的原始的判定方法符号语言(判定)
∵ AB//CD,AD//BC
∴四边形ABCD是平行四边形
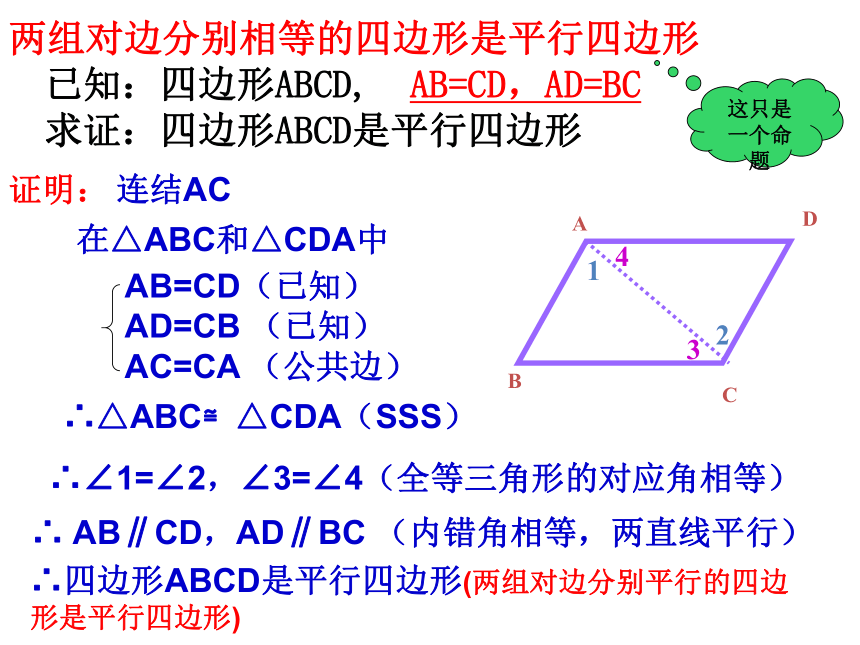
思考平行四边形的两组对边分别相等;平行四边形的两组对角分别相等;我们得到的这些逆命题都成立?我们一起探讨一下吧:平行四边形的对角线互相平分。思考:我们已经学习了平行四边形的这些性质,那么它们的逆命题各是什么呢?两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形。两组对边分别相等的四边形是平行四边形;已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形证明:连结AC在△ABC和△CDA中∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
DBAC2134∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
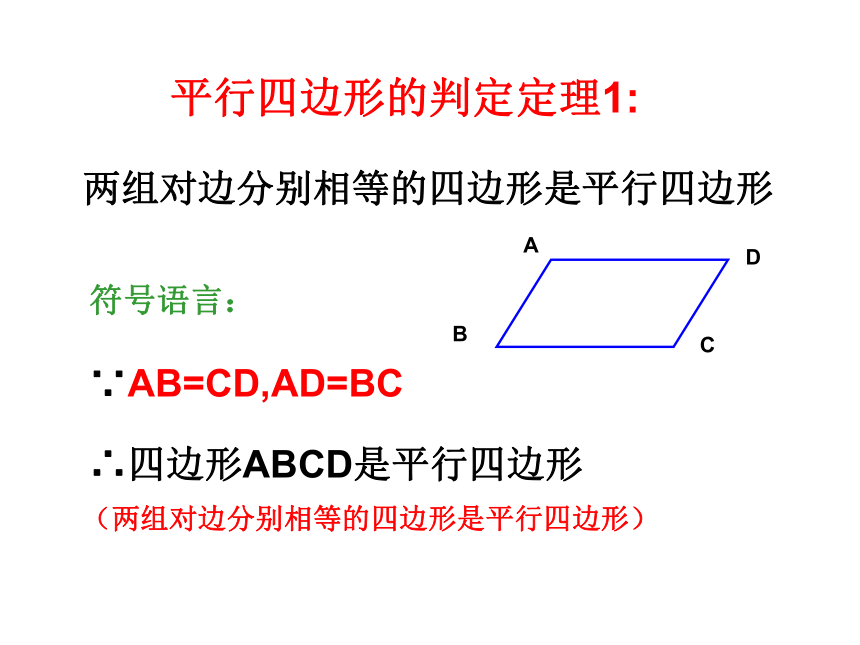
两组对边分别相等的四边形是平行四边形
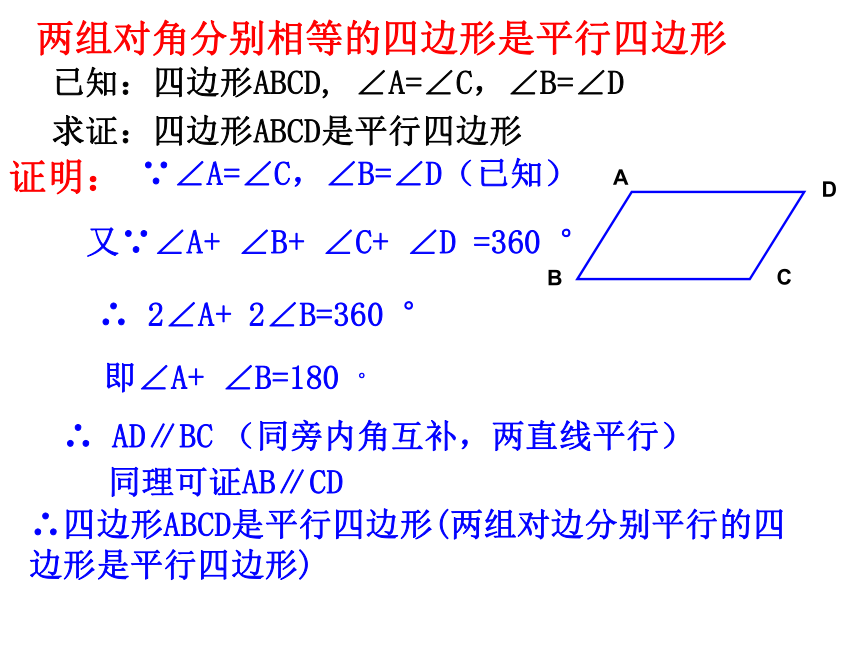
这只是一个命题两组对边分别相等的四边形是平行四边形平行四边形的判定定理1:符号语言:∵AB=CD,AD=BC∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行)
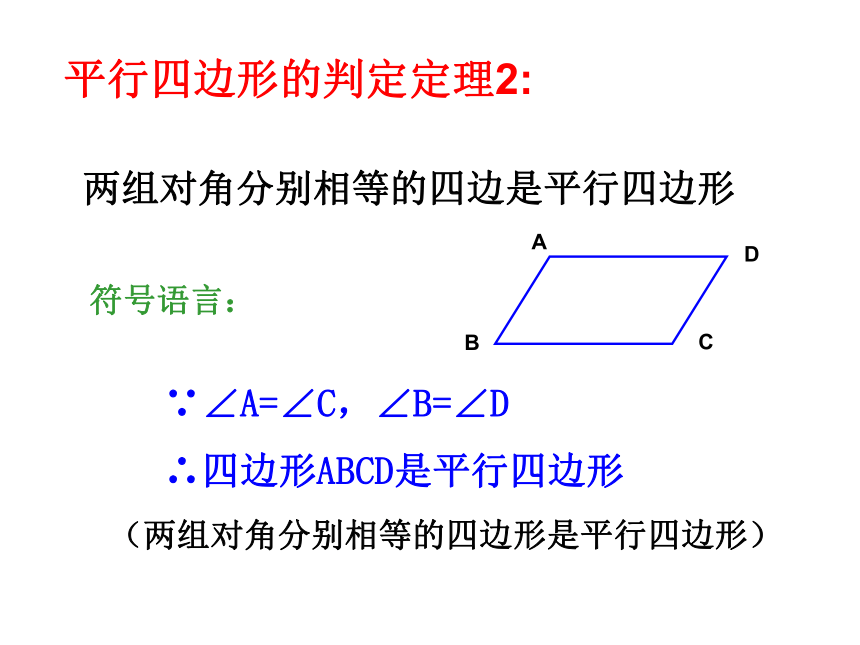
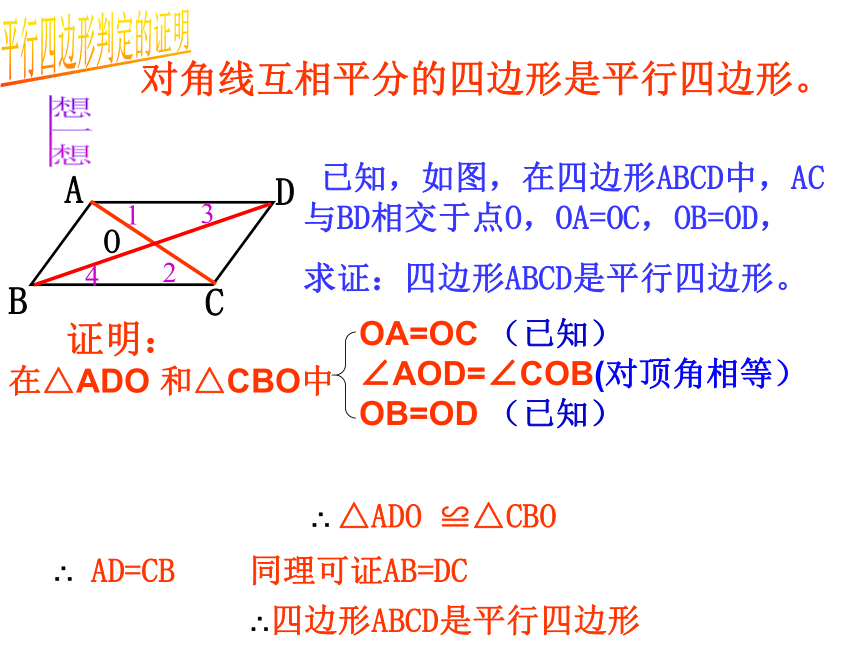
两组对角分别相等的四边形是平行四边形两组对角分别相等的四边是平行四边形平行四边形的判定定理2:符号语言:∵∠A=∠C,∠B=∠D∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形)对角线互相平分的四边形是平行四边形。 已知,如图,在四边形ABCD中,AC与BD相交于点O,OA=OC,OB=OD,
求证:四边形ABCD是平行四边形。同理可证AB=DC∴ △ADO ≌△CBO∴ AD=CB 平行四边形判定的证明证明:想一想∴四边形ABCD是平行四边形在△ADO 和△CBO中
对角线互相平分的四边形是平行四边形平行四边形的判定定理3:符号语言:O∵ OA=OC,OB=OD∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形)试一试判断下列四边形是否是平行四边形?并口述理由.BADC⑴⑶ABCDO5㎝5㎝4㎝4㎝4.8㎝BADC4.8㎝7.6㎝7.6㎝⑵AB∥CD大显身手证法1: 同理可证:BE=DF例1.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形∵四边形ABCD是平行四边形大显身手例1.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DOABCEF证法2:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
及时训练
1.下列条件能判断四边形ABDC是平行四边形的是( )
A.AB∥CD,AC=B D
B.AB= CD AC=B D
C.AB=CD,AD=BC
D.AB=CD,OA=OC
2.已知:如图,平行四边形ABCD中,点E、F分别在CD、AB上,DF∥BE,EF交BD于点O.求证: OE=OF.证明:连接BD交AC于点O.
∵四边形ABCD是平行四边形
∴BO=DO
又∵ EO=FO
∴ 四边形BFDE是平行四边形 已知:E、F是平行四边形ABCD对角线AC上的两点,并且OE=OF.
求证:四边形BFDE是平行四边形DOABCEF 2、 如图,AB=DC=EF,AD=BC,DE=CF,图中有哪些互相平行的线段?解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF AD∥BC AB=DC AD=BC四边形ABCD是平行四边形AB∥DCDC∥EF DC=EF DE=CF四边形CDEF是平行四边形DE∥CFAB∥ DC∥EF分析: 一天八年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战想一想方法(一)D(两组对边分别平行的四边形是平行四边形)∵AB∥CD,AD∥BC ∴四边形ABCD是平行四边形方法(二)D两组对边分别相等的四边形是平行四边形?方法(三)DO对角线互相平分的四边形是平行四边形 我们知道,如果一个四边形是平行四边形,那么它的任意一组对边平行且相等。反过来,一组对边平行且相等的四边形是平行四边形?如图,在四边形ABCD中,AD//BC,AD=BC.
求证:四边形ABCD是平行四边形.
平行四边判定定理4:一组对边平行且相等的四边形是平行四边形。一组对边平行且相等的四边形是平行四边形。平行四边形的判定定理4:符号语言:∵AB//CD,AB=CD.∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)从边来判定1、两组对边分别平行的四边形是平行四边形 2、两组对边分别相等的四边形是平行四边形从角来判定4、两组对角分别相等的四边形是平行四边形从对角线来判定5、两条对角线互相平分的四边形是平行四边形理一理平行四边形的判定方法3、一组对边平行且相等的四边形是平行四边形作业第47页 2、4
第50页 4、6
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD 平行四边形是中心对称图形平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形
符号语言 (性质)
∵四边形ABCD是平行四边形
∴ AB//CD,AD//BC定义是平行四边形的原始的判定方法符号语言(判定)
∵ AB//CD,AD//BC
∴四边形ABCD是平行四边形
思考平行四边形的两组对边分别相等;平行四边形的两组对角分别相等;我们得到的这些逆命题都成立?我们一起探讨一下吧:平行四边形的对角线互相平分。思考:我们已经学习了平行四边形的这些性质,那么它们的逆命题各是什么呢?两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形。两组对边分别相等的四边形是平行四边形;已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形证明:连结AC在△ABC和△CDA中∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
DBAC2134∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
两组对边分别相等的四边形是平行四边形
这只是一个命题两组对边分别相等的四边形是平行四边形平行四边形的判定定理1:符号语言:∵AB=CD,AD=BC∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行)
两组对角分别相等的四边形是平行四边形两组对角分别相等的四边是平行四边形平行四边形的判定定理2:符号语言:∵∠A=∠C,∠B=∠D∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形)对角线互相平分的四边形是平行四边形。 已知,如图,在四边形ABCD中,AC与BD相交于点O,OA=OC,OB=OD,
求证:四边形ABCD是平行四边形。同理可证AB=DC∴ △ADO ≌△CBO∴ AD=CB 平行四边形判定的证明证明:想一想∴四边形ABCD是平行四边形在△ADO 和△CBO中
对角线互相平分的四边形是平行四边形平行四边形的判定定理3:符号语言:O∵ OA=OC,OB=OD∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形)试一试判断下列四边形是否是平行四边形?并口述理由.BADC⑴⑶ABCDO5㎝5㎝4㎝4㎝4.8㎝BADC4.8㎝7.6㎝7.6㎝⑵AB∥CD大显身手证法1: 同理可证:BE=DF例1.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形∵四边形ABCD是平行四边形大显身手例1.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DOABCEF证法2:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
及时训练
1.下列条件能判断四边形ABDC是平行四边形的是( )
A.AB∥CD,AC=B D
B.AB= CD AC=B D
C.AB=CD,AD=BC
D.AB=CD,OA=OC
2.已知:如图,平行四边形ABCD中,点E、F分别在CD、AB上,DF∥BE,EF交BD于点O.求证: OE=OF.证明:连接BD交AC于点O.
∵四边形ABCD是平行四边形
∴BO=DO
又∵ EO=FO
∴ 四边形BFDE是平行四边形 已知:E、F是平行四边形ABCD对角线AC上的两点,并且OE=OF.
求证:四边形BFDE是平行四边形DOABCEF 2、 如图,AB=DC=EF,AD=BC,DE=CF,图中有哪些互相平行的线段?解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF AD∥BC AB=DC AD=BC四边形ABCD是平行四边形AB∥DCDC∥EF DC=EF DE=CF四边形CDEF是平行四边形DE∥CFAB∥ DC∥EF分析: 一天八年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战想一想方法(一)D(两组对边分别平行的四边形是平行四边形)∵AB∥CD,AD∥BC ∴四边形ABCD是平行四边形方法(二)D两组对边分别相等的四边形是平行四边形?方法(三)DO对角线互相平分的四边形是平行四边形 我们知道,如果一个四边形是平行四边形,那么它的任意一组对边平行且相等。反过来,一组对边平行且相等的四边形是平行四边形?如图,在四边形ABCD中,AD//BC,AD=BC.
求证:四边形ABCD是平行四边形.
平行四边判定定理4:一组对边平行且相等的四边形是平行四边形。一组对边平行且相等的四边形是平行四边形。平行四边形的判定定理4:符号语言:∵AB//CD,AB=CD.∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)从边来判定1、两组对边分别平行的四边形是平行四边形 2、两组对边分别相等的四边形是平行四边形从角来判定4、两组对角分别相等的四边形是平行四边形从对角线来判定5、两条对角线互相平分的四边形是平行四边形理一理平行四边形的判定方法3、一组对边平行且相等的四边形是平行四边形作业第47页 2、4
第50页 4、6
