2017-2018学年八年级数学下册第18章平行四边形18.1.1平行四边形的性质(第1课时)一课一练基础闯关(含解析)
文档属性
| 名称 | 2017-2018学年八年级数学下册第18章平行四边形18.1.1平行四边形的性质(第1课时)一课一练基础闯关(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 235.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-20 23:40:15 | ||
图片预览


文档简介
平行四边形的性质
一课一练·基础闯关
题组利用平行四边形的边角性质进行计算
如图,在?ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是
( )
A.45° B.55° C.65° D.75°
【解析】选A.∵四边形ABCD是平行四边形,
∴∠A=∠BCD=135°,
∴∠MCD=180°-∠DCB=180°-135°=45°.
2.如图,在平行四边形ABCD中,AB=4,BC=6,AC的垂直平分线交AD于点E,则△CDE的周长是 ( )
A.7 B.10 C.11 D.12
【解析】选B.∵AC的垂直平分线交AD于点E,∴AE=EC,
∵四边形ABCD为平行四边形,∴AB=CD=4,BC=AD=6,∴△CDE的周长=EC+DE+CD=AE+DE+CD=AD+CD=10.
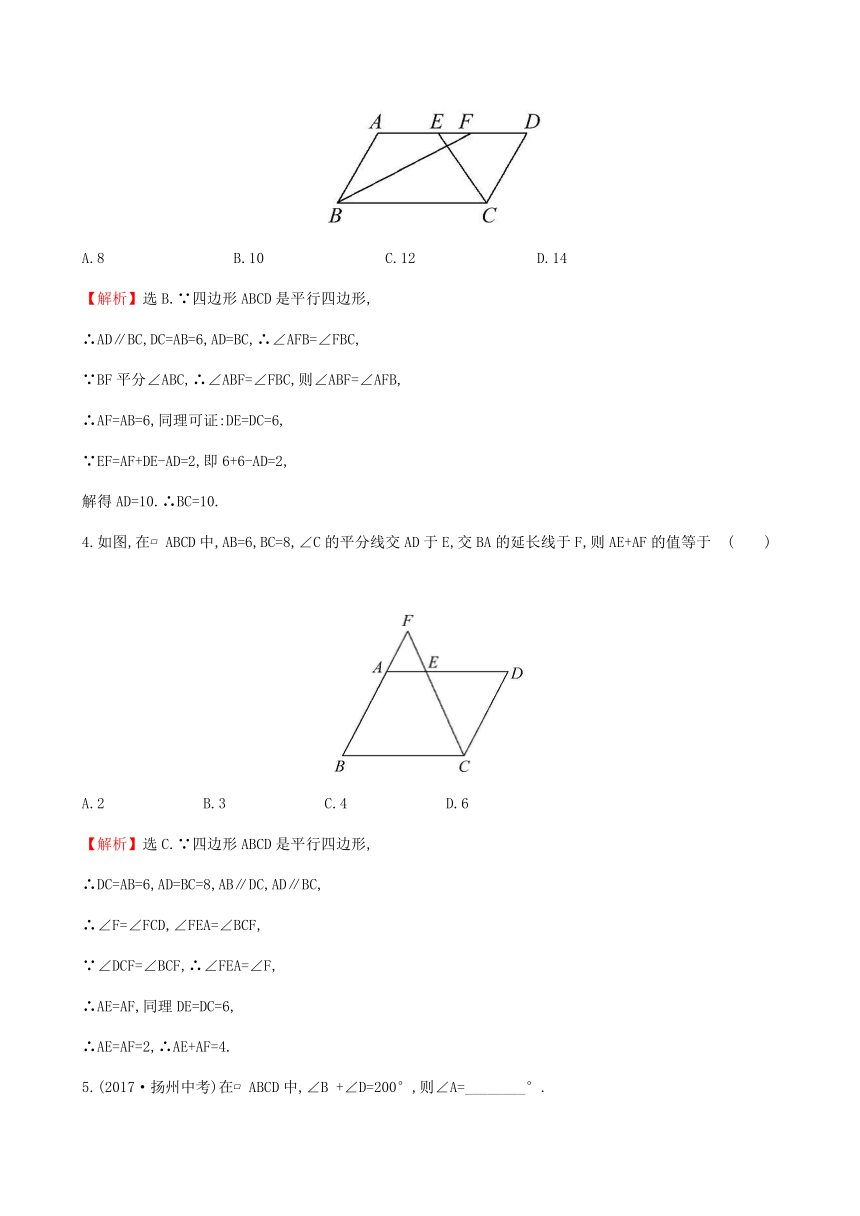
3.如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为 ( )
A.8 B.10 C.12 D.14
【解析】选B.∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB=6,AD=BC,∴∠AFB=∠FBC,
∵BF平分∠ABC,∴∠ABF=∠FBC,则∠ABF=∠AFB,
∴AF=AB=6,同理可证:DE=DC=6,
∵EF=AF+DE-AD=2,即6+6-AD=2,
解得AD=10.∴BC=10.
4.如图,在?ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于 ( )
A.2 B.3 C.4 D.6
【解析】选C.∵四边形ABCD是平行四边形,
∴DC=AB=6,AD=BC=8,AB∥DC,AD∥BC,
∴∠F=∠FCD,∠FEA=∠BCF,
∵∠DCF=∠BCF,∴∠FEA=∠F,
∴AE=AF,同理DE=DC=6,
∴AE=AF=2,∴AE+AF=4.
5.(2017·扬州中考)在?ABCD中,∠B +∠D=200°,则∠A=________°.
【解析】根据“平行四边形的对角相等、邻角互补”可以求得∠A=180°-200°÷2=80°.
答案:80
6.如图,在?ABCD中,AB=2cm,AD=4cm,AC⊥BC,则△DBC比△ABC的周长长________cm.
【解析】在?ABCD中,∵AB=CD=2cm,AD=BC=4cm,AO=CO,BO=DO,∵AC⊥BC,∴AC==6cm,∴OC=3cm,∴BO==5cm,∴BD=10cm,∴△DBC的周长-△ABC的周长=BC+CD+BD-(AB+BC+AC)=BD-AC=10-6=4(cm).
答案:4
(2017·菏泽中考)如图,E是?ABCD的边AD的中点,连接CE并延长交BA的延长线于F,若CD=6,求BF的长.
【解析】∵四边形ABCD是平行四边形,∴AF∥DC,AB=DC,∴∠F=∠DCF,
∵点E是?ABCD的边AD的中点,∴AE=DE,
∵∠AEF=∠DEC,∴△AEF≌△DEC,∴AF=CD=6,
∴点A是BF的中点,即BF=2CD=12.
题组利用平行四边形的边角性质进行证明
1.(2017·乌鲁木齐中考)如图,四边形ABCD是平行四边形,E,F是对角线BD上的两点,且BF=ED,
求证:AE∥CF.
【证明】∵四边形ABCD是平行四边形,
∴AD∥BC且AD=BC,
∴∠ADE=∠CBF,
又∵BF=ED,∴△AED≌△CFB(SAS),
∴∠AED=∠CFB,∴AE∥CF.
2.(2017·益阳中考)如图,四边形ABCD为平行四边形,F是CD的中点,连接AF并延长与BC的延长线交于点E.求证:BC = CE.
【证明】∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∴∠DAF=∠E,∠ADF =∠ECF,
又∵F是CD的中点,即DF=CF,
∴△ADF≌△ECF.
∴AD=CE.∴BC=CE.
(2017·南京中考)如图,在?ABCD中,点E,F分别在AD,BC上,且AE=CF,EF,BD相交于点O.
求证:OE=OF.
【证明】∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴∠EDO=∠FBO,∠DEO=∠BFO.
∵AE=CF,
∴AD-AE=CB-CF,即DE=BF.
∴△DOE≌△BOF.
∴OE=OF.
如图1,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是
( )
图1
A.10cm B.8cm C.6cm D.4cm
【解析】选D.∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,AD∥BC,∴∠DAE=∠AEB,∵AE平分∠BAD,∴∠DAE=∠BAE,∴∠BAE=∠AEB,∴AB=BE,设AB=CD=xcm,则AD=BC=(x+2)cm,
∵?ABCD的周长为20cm,∴x+x+2=10,解得x=4,即AB=4cm.
【母题变式】
[变式一]如图2,在?ABCD中,∠ABC的平分线BM交CD于点M,且MC=2,?ABCD的周长是14,则DM等于 ( )
图2
A.1 B.2 C.3 D.4
【解析】选C.∵在?ABCD中,BM是∠ABC的平分线,∴∠CBM=∠CMB=∠ABM,∴BC=MC=2,∵?ABCD的周长是14,∴AB=CD=5,∴DM=3.
[变式二]如图3,在?ABCD中,已知AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长为 ( )
图3
A.8cm B.6cm C.4cm D.2cm
【解析】选C.∵AD∥BC,∴∠DAE=∠AEB,∵AE平分∠BAD,∴∠DAE=∠AEB=∠BAE,
∴BE=AB=8cm,∵BC=AD=12cm,∴CE=4cm.
[变式三](2017·十堰模拟)如图,在平行四边形ABCD中,DE平分∠ADC,BE=2,DC=4,则平行四边形ABCD的周长为 ( )
A.16 B.24 C.20 D.12
【解析】选C.∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠ADE=∠CED,
∵DE平分∠ADC,∴∠ADE=∠CDE,
∴∠CED=∠CDE,∴CE=CD=4,
∴BC=BE+CE=6,
∴?ABCD的周长为:2×(4+6)=20.
[变式一]如图,在平行四边形ABCD中,AB=5cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=________cm.
【解析】由四边形ABCD为平行四边形及BF平分∠ABC可知∠CBF=∠CFB,所以CF=CB=AD=7cm,所以DF=CF-CD=2cm.
答案:2
[变式二]如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为 ( )
A.2 B.4 C.4 D.8
【解析】选B.∵AE为∠BAD的平分线,∴∠DAE=∠BAE,∵DC∥AB,∴∠BAE=∠DFA,∴∠DAE=∠DFA,∴AD=FD,又F为DC的中点,∴DF=CF,
∴AD=DF=DC=AB=2,在Rt△ADG中,根据勾股定理得:AG=,则AF=2AG=2,在△ADF和△ECF中,∴△ADF≌△ECF(AAS),∴AF=EF,则AE=2AF=4.
一课一练·基础闯关
题组利用平行四边形的边角性质进行计算
如图,在?ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是
( )
A.45° B.55° C.65° D.75°
【解析】选A.∵四边形ABCD是平行四边形,
∴∠A=∠BCD=135°,
∴∠MCD=180°-∠DCB=180°-135°=45°.
2.如图,在平行四边形ABCD中,AB=4,BC=6,AC的垂直平分线交AD于点E,则△CDE的周长是 ( )
A.7 B.10 C.11 D.12
【解析】选B.∵AC的垂直平分线交AD于点E,∴AE=EC,
∵四边形ABCD为平行四边形,∴AB=CD=4,BC=AD=6,∴△CDE的周长=EC+DE+CD=AE+DE+CD=AD+CD=10.
3.如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为 ( )
A.8 B.10 C.12 D.14
【解析】选B.∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB=6,AD=BC,∴∠AFB=∠FBC,
∵BF平分∠ABC,∴∠ABF=∠FBC,则∠ABF=∠AFB,
∴AF=AB=6,同理可证:DE=DC=6,
∵EF=AF+DE-AD=2,即6+6-AD=2,
解得AD=10.∴BC=10.
4.如图,在?ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于 ( )
A.2 B.3 C.4 D.6
【解析】选C.∵四边形ABCD是平行四边形,
∴DC=AB=6,AD=BC=8,AB∥DC,AD∥BC,
∴∠F=∠FCD,∠FEA=∠BCF,
∵∠DCF=∠BCF,∴∠FEA=∠F,
∴AE=AF,同理DE=DC=6,
∴AE=AF=2,∴AE+AF=4.
5.(2017·扬州中考)在?ABCD中,∠B +∠D=200°,则∠A=________°.
【解析】根据“平行四边形的对角相等、邻角互补”可以求得∠A=180°-200°÷2=80°.
答案:80
6.如图,在?ABCD中,AB=2cm,AD=4cm,AC⊥BC,则△DBC比△ABC的周长长________cm.
【解析】在?ABCD中,∵AB=CD=2cm,AD=BC=4cm,AO=CO,BO=DO,∵AC⊥BC,∴AC==6cm,∴OC=3cm,∴BO==5cm,∴BD=10cm,∴△DBC的周长-△ABC的周长=BC+CD+BD-(AB+BC+AC)=BD-AC=10-6=4(cm).
答案:4
(2017·菏泽中考)如图,E是?ABCD的边AD的中点,连接CE并延长交BA的延长线于F,若CD=6,求BF的长.
【解析】∵四边形ABCD是平行四边形,∴AF∥DC,AB=DC,∴∠F=∠DCF,
∵点E是?ABCD的边AD的中点,∴AE=DE,
∵∠AEF=∠DEC,∴△AEF≌△DEC,∴AF=CD=6,
∴点A是BF的中点,即BF=2CD=12.
题组利用平行四边形的边角性质进行证明
1.(2017·乌鲁木齐中考)如图,四边形ABCD是平行四边形,E,F是对角线BD上的两点,且BF=ED,
求证:AE∥CF.
【证明】∵四边形ABCD是平行四边形,
∴AD∥BC且AD=BC,
∴∠ADE=∠CBF,
又∵BF=ED,∴△AED≌△CFB(SAS),
∴∠AED=∠CFB,∴AE∥CF.
2.(2017·益阳中考)如图,四边形ABCD为平行四边形,F是CD的中点,连接AF并延长与BC的延长线交于点E.求证:BC = CE.
【证明】∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∴∠DAF=∠E,∠ADF =∠ECF,
又∵F是CD的中点,即DF=CF,
∴△ADF≌△ECF.
∴AD=CE.∴BC=CE.
(2017·南京中考)如图,在?ABCD中,点E,F分别在AD,BC上,且AE=CF,EF,BD相交于点O.
求证:OE=OF.
【证明】∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴∠EDO=∠FBO,∠DEO=∠BFO.
∵AE=CF,
∴AD-AE=CB-CF,即DE=BF.
∴△DOE≌△BOF.
∴OE=OF.
如图1,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是
( )
图1
A.10cm B.8cm C.6cm D.4cm
【解析】选D.∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,AD∥BC,∴∠DAE=∠AEB,∵AE平分∠BAD,∴∠DAE=∠BAE,∴∠BAE=∠AEB,∴AB=BE,设AB=CD=xcm,则AD=BC=(x+2)cm,
∵?ABCD的周长为20cm,∴x+x+2=10,解得x=4,即AB=4cm.
【母题变式】
[变式一]如图2,在?ABCD中,∠ABC的平分线BM交CD于点M,且MC=2,?ABCD的周长是14,则DM等于 ( )
图2
A.1 B.2 C.3 D.4
【解析】选C.∵在?ABCD中,BM是∠ABC的平分线,∴∠CBM=∠CMB=∠ABM,∴BC=MC=2,∵?ABCD的周长是14,∴AB=CD=5,∴DM=3.
[变式二]如图3,在?ABCD中,已知AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长为 ( )
图3
A.8cm B.6cm C.4cm D.2cm
【解析】选C.∵AD∥BC,∴∠DAE=∠AEB,∵AE平分∠BAD,∴∠DAE=∠AEB=∠BAE,
∴BE=AB=8cm,∵BC=AD=12cm,∴CE=4cm.
[变式三](2017·十堰模拟)如图,在平行四边形ABCD中,DE平分∠ADC,BE=2,DC=4,则平行四边形ABCD的周长为 ( )
A.16 B.24 C.20 D.12
【解析】选C.∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠ADE=∠CED,
∵DE平分∠ADC,∴∠ADE=∠CDE,
∴∠CED=∠CDE,∴CE=CD=4,
∴BC=BE+CE=6,
∴?ABCD的周长为:2×(4+6)=20.
[变式一]如图,在平行四边形ABCD中,AB=5cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=________cm.
【解析】由四边形ABCD为平行四边形及BF平分∠ABC可知∠CBF=∠CFB,所以CF=CB=AD=7cm,所以DF=CF-CD=2cm.
答案:2
[变式二]如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为 ( )
A.2 B.4 C.4 D.8
【解析】选B.∵AE为∠BAD的平分线,∴∠DAE=∠BAE,∵DC∥AB,∴∠BAE=∠DFA,∴∠DAE=∠DFA,∴AD=FD,又F为DC的中点,∴DF=CF,
∴AD=DF=DC=AB=2,在Rt△ADG中,根据勾股定理得:AG=,则AF=2AG=2,在△ADF和△ECF中,∴△ADF≌△ECF(AAS),∴AF=EF,则AE=2AF=4.
