2017-2018学年八年级数学下册第18章平行四边形18.1.1平行四边形的性质(第2课时)一课一练基础闯关(含解析)(新版)新人教版
文档属性
| 名称 | 2017-2018学年八年级数学下册第18章平行四边形18.1.1平行四边形的性质(第2课时)一课一练基础闯关(含解析)(新版)新人教版 |  | |
| 格式 | zip | ||
| 文件大小 | 281.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-21 18:33:59 | ||
图片预览


文档简介
平行四边形的性质
一课一练·基础闯关
题组平行四边形的对角线性质的应用
1.平行四边形的对角线一定具有的性质是 ( )
A.相等 B.互相平分
C.互相垂直 D.互相垂直且相等
【解析】选B.平行四边形的对角线互相平分,不一定相等和垂直.
2.(2017·广东模拟)如图所示,在平行四边形ABCD中,O为对角线AC,BD的交点,与△AOD全等的是 ( )
A.△ABC B.△ADC C.△BCD D.△COB
【解析】选D.∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠DAO=∠BCO,∠ADO=∠CBO,AD=BC,
∴△AOD≌△COB(ASA).
3.如图,?ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是
( )
A.10 B.14 C.20 D.22
【解析】选B.∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,DC=AB=6,
∵AC+BD=16,
∴AO+BO=8,
∴△ABO的周长是14.
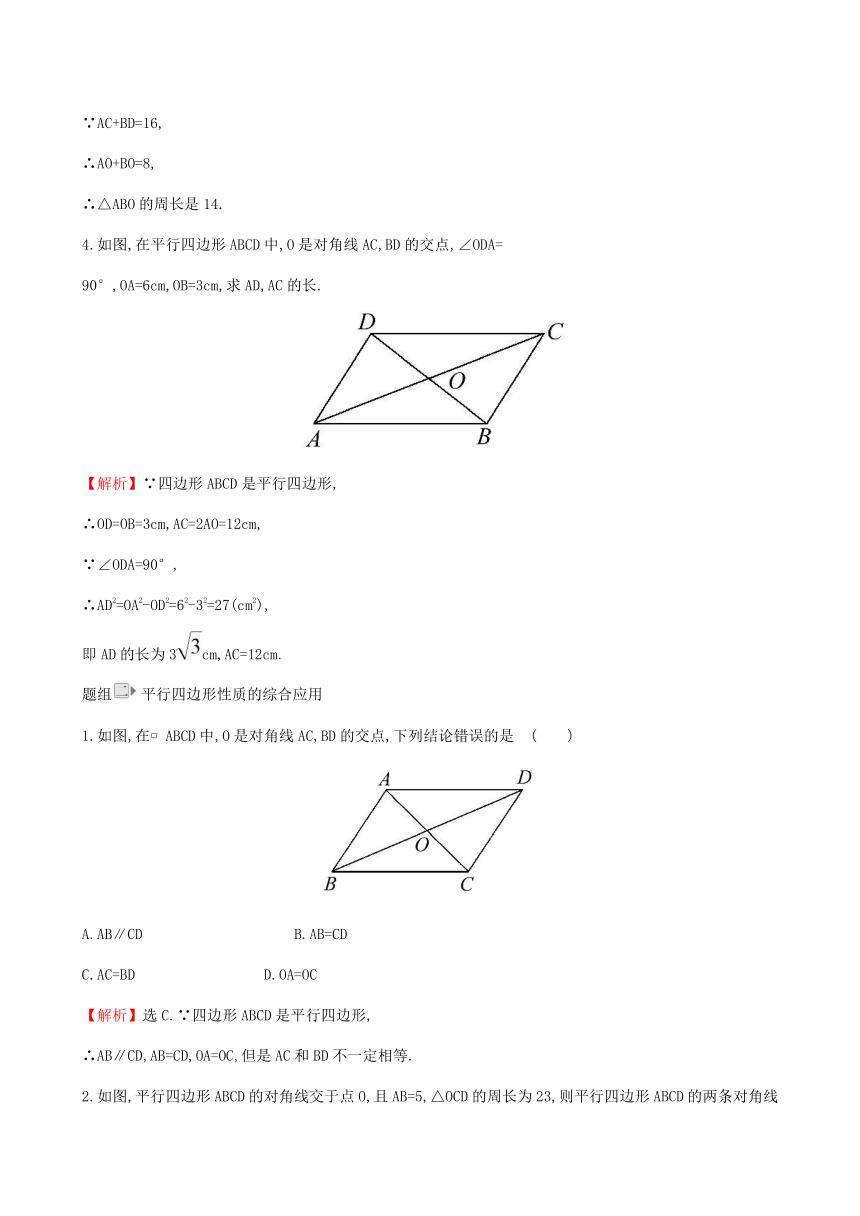
4.如图,在平行四边形ABCD中,O是对角线AC,BD的交点,∠ODA=
90°,OA=6cm,OB=3cm,求AD,AC的长.
【解析】∵四边形ABCD是平行四边形,
∴OD=OB=3cm,AC=2AO=12cm,
∵∠ODA=90°,
∴AD2=OA2-OD2=62-32=27(cm2),
即AD的长为3cm,AC=12cm.
题组平行四边形性质的综合应用
1.如图,在?ABCD中,O是对角线AC,BD的交点,下列结论错误的是 ( )
A.AB∥CD B.AB=CD
C.AC=BD D.OA=OC
【解析】选C.∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,OA=OC,但是AC和BD不一定相等.
2.如图,平行四边形ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是( )
A.18 B.28 C.36 D.46
【解析】选C.∵四边形ABCD是平行四边形,
∴CD=AB=5,
∵△OCD的周长为23,∴OD+OC=23-5=18,
∵BD=2DO,AC=2OC,
∴平行四边形ABCD的两条对角线的和=BD+AC=2(DO+OC)=36.
3.(2017·眉山中考)如图,EF过?ABCD对角线的交点O,交AD于点E,交BC于点F.若?ABCD的周长为18,OE=1.5,则四边形EFCD的周长为 ( )
A.14 B.13 C.12 D.10
【解析】选C.因为四边形ABCD是平行四边形,
所以AD∥BC,OA=OC,所以∠OAE=∠OCF,
又因为∠AOE=∠COF,所以△AOE≌△COF,
所以AE=CF,OE=OF,而AB=CD,AD=BC,
所以四边形EFCD的周长为AD+CD+EF=×18+2×1.5=12.
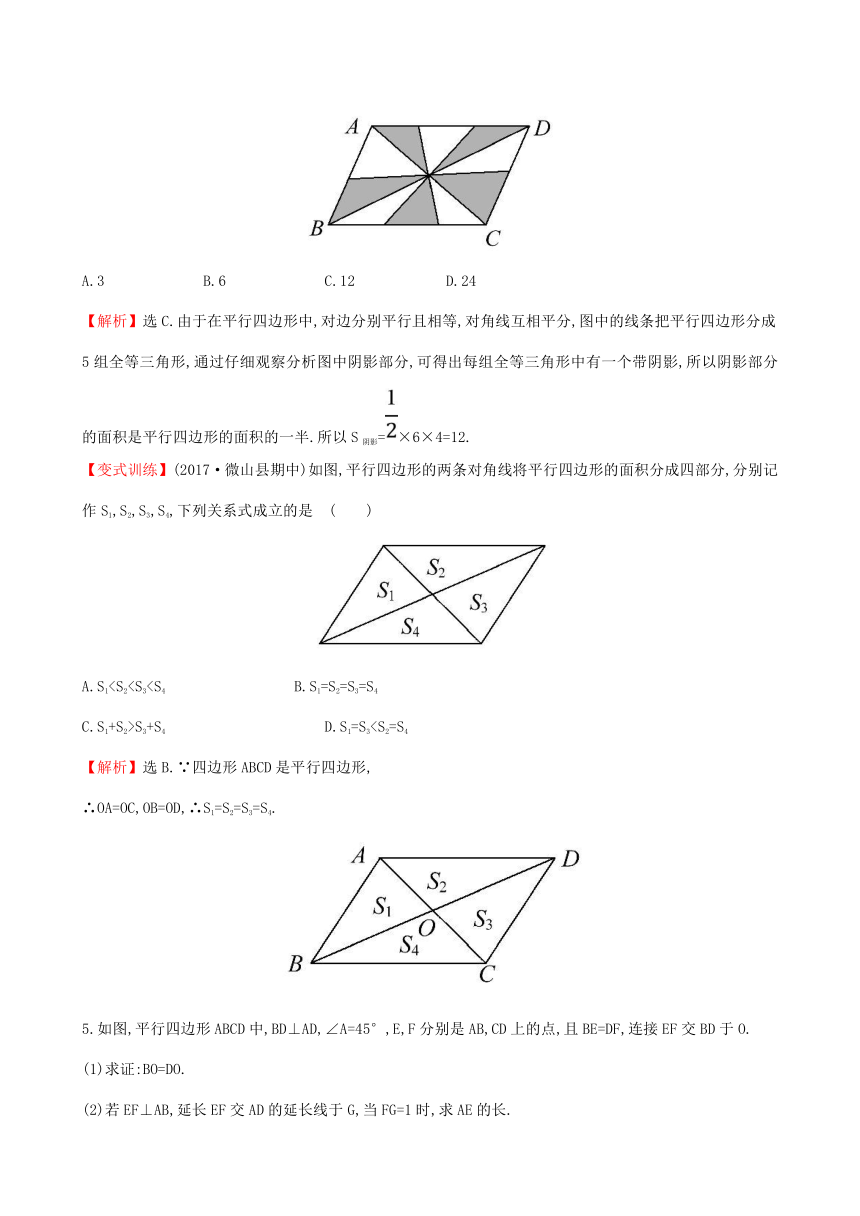
4.如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为 ( )
A.3 B.6 C.12 D.24
【解析】选C.由于在平行四边形中,对边分别平行且相等,对角线互相平分,图中的线条把平行四边形分成5组全等三角形,通过仔细观察分析图中阴影部分,可得出每组全等三角形中有一个带阴影,所以阴影部分的面积是平行四边形的面积的一半.所以S阴影=×6×4=12.
【变式训练】(2017·微山县期中)如图,平行四边形的两条对角线将平行四边形的面积分成四部分,分别记作S1,S2,S3,S4,下列关系式成立的是 ( )
A.S1C.S1+S2>S3+S4 D.S1=S3【解析】选B.∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,∴S1=S2=S3=S4.
5.如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E,F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO.
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
【解题指南】(1)由平行四边形的性质和AAS证明△OBE≌△ODF,得出对应边相等即可.
(2)证出AE=GE,再证明DG=DO,得出OF=FG=1,即可得出结果.
【解析】(1)∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠OBE=∠ODF.
在△OBE与△ODF中,
∴△OBE≌△ODF(AAS).
∴BO=DO.
(2)∵EF⊥AB,AB∥DC,
∴∠GEA=∠GFD=90°,
∵∠A=45°,∴∠G=∠A=45°.
∴AE=GE.
∵BD⊥AD,∴∠ADB=∠GDO=90°.
∴∠GOD=∠G=45°.
∴DG=DO,
∴OF=FG=1,
由(1)可知,OE=OF=1,
∴GE=OE+OF+FG=3,
∴AE=3.
如图,在?ABCD中,对角线AC,BD交于点O,经过点O的直线交AB于E,交CD于F.
求证:OE=OF.
【证明】∵四边形ABCD是平行四边形,∴AO=CO,AB∥CD,∴∠EAO=∠FCO.
又∵∠AOE=∠COF,∴△AOE≌△COF(ASA),
∴OE=OF.
【母题变式】
[变式一]如图,在?ABCD中,对角线AC与BD相交于O,EF是过点O的任一直线,交AD于点E,交BC于点F,猜想OE和OF的数量关系,并说明理由.
【解析】结论:OE=OF.
理由:∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠OAE=∠OCF,
在△AOE和△COF中,
∴△AOE≌△COF,∴OE=OF.
[变式二](2017·广安月考)如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O任作一条直线分别交AB,CD于点E,F.
若AB=7,BC=5,OE=2,求四边形BCFE的周长.
【解析】∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD,
∴∠OAE=∠OCF,
在△OAE和△OCF中,
∴△AOE≌△COF(ASA),
∴CF=AE,OE=OF,
∵AB=7,BC=5,OE=2,
∴EF=2OE=4,BE+CF=BE+AE=AB=7,
∴四边形BCFE的周长为:EF+BE+BC+CF=4+7+5=16.
[变式]在?ABCD中,对角线AC,BD交于点O,过点O作直线EF分别交线段AD,BC于点E,F.
(1)根据题意画出图形,并标上正确的字母.
(2)求证:DE=BF.
【解析】(1)作图如图:
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,OB=OD,
∴∠EDO=∠FBO,
在△DOE和△BOF中
∴△DOE≌△BOF.∴DE=BF.
一课一练·基础闯关
题组平行四边形的对角线性质的应用
1.平行四边形的对角线一定具有的性质是 ( )
A.相等 B.互相平分
C.互相垂直 D.互相垂直且相等
【解析】选B.平行四边形的对角线互相平分,不一定相等和垂直.
2.(2017·广东模拟)如图所示,在平行四边形ABCD中,O为对角线AC,BD的交点,与△AOD全等的是 ( )
A.△ABC B.△ADC C.△BCD D.△COB
【解析】选D.∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠DAO=∠BCO,∠ADO=∠CBO,AD=BC,
∴△AOD≌△COB(ASA).
3.如图,?ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是
( )
A.10 B.14 C.20 D.22
【解析】选B.∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,DC=AB=6,
∵AC+BD=16,
∴AO+BO=8,
∴△ABO的周长是14.
4.如图,在平行四边形ABCD中,O是对角线AC,BD的交点,∠ODA=
90°,OA=6cm,OB=3cm,求AD,AC的长.
【解析】∵四边形ABCD是平行四边形,
∴OD=OB=3cm,AC=2AO=12cm,
∵∠ODA=90°,
∴AD2=OA2-OD2=62-32=27(cm2),
即AD的长为3cm,AC=12cm.
题组平行四边形性质的综合应用
1.如图,在?ABCD中,O是对角线AC,BD的交点,下列结论错误的是 ( )
A.AB∥CD B.AB=CD
C.AC=BD D.OA=OC
【解析】选C.∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,OA=OC,但是AC和BD不一定相等.
2.如图,平行四边形ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是( )
A.18 B.28 C.36 D.46
【解析】选C.∵四边形ABCD是平行四边形,
∴CD=AB=5,
∵△OCD的周长为23,∴OD+OC=23-5=18,
∵BD=2DO,AC=2OC,
∴平行四边形ABCD的两条对角线的和=BD+AC=2(DO+OC)=36.
3.(2017·眉山中考)如图,EF过?ABCD对角线的交点O,交AD于点E,交BC于点F.若?ABCD的周长为18,OE=1.5,则四边形EFCD的周长为 ( )
A.14 B.13 C.12 D.10
【解析】选C.因为四边形ABCD是平行四边形,
所以AD∥BC,OA=OC,所以∠OAE=∠OCF,
又因为∠AOE=∠COF,所以△AOE≌△COF,
所以AE=CF,OE=OF,而AB=CD,AD=BC,
所以四边形EFCD的周长为AD+CD+EF=×18+2×1.5=12.
4.如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为 ( )
A.3 B.6 C.12 D.24
【解析】选C.由于在平行四边形中,对边分别平行且相等,对角线互相平分,图中的线条把平行四边形分成5组全等三角形,通过仔细观察分析图中阴影部分,可得出每组全等三角形中有一个带阴影,所以阴影部分的面积是平行四边形的面积的一半.所以S阴影=×6×4=12.
【变式训练】(2017·微山县期中)如图,平行四边形的两条对角线将平行四边形的面积分成四部分,分别记作S1,S2,S3,S4,下列关系式成立的是 ( )
A.S1
∴OA=OC,OB=OD,∴S1=S2=S3=S4.
5.如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E,F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO.
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
【解题指南】(1)由平行四边形的性质和AAS证明△OBE≌△ODF,得出对应边相等即可.
(2)证出AE=GE,再证明DG=DO,得出OF=FG=1,即可得出结果.
【解析】(1)∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠OBE=∠ODF.
在△OBE与△ODF中,
∴△OBE≌△ODF(AAS).
∴BO=DO.
(2)∵EF⊥AB,AB∥DC,
∴∠GEA=∠GFD=90°,
∵∠A=45°,∴∠G=∠A=45°.
∴AE=GE.
∵BD⊥AD,∴∠ADB=∠GDO=90°.
∴∠GOD=∠G=45°.
∴DG=DO,
∴OF=FG=1,
由(1)可知,OE=OF=1,
∴GE=OE+OF+FG=3,
∴AE=3.
如图,在?ABCD中,对角线AC,BD交于点O,经过点O的直线交AB于E,交CD于F.
求证:OE=OF.
【证明】∵四边形ABCD是平行四边形,∴AO=CO,AB∥CD,∴∠EAO=∠FCO.
又∵∠AOE=∠COF,∴△AOE≌△COF(ASA),
∴OE=OF.
【母题变式】
[变式一]如图,在?ABCD中,对角线AC与BD相交于O,EF是过点O的任一直线,交AD于点E,交BC于点F,猜想OE和OF的数量关系,并说明理由.
【解析】结论:OE=OF.
理由:∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠OAE=∠OCF,
在△AOE和△COF中,
∴△AOE≌△COF,∴OE=OF.
[变式二](2017·广安月考)如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O任作一条直线分别交AB,CD于点E,F.
若AB=7,BC=5,OE=2,求四边形BCFE的周长.
【解析】∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD,
∴∠OAE=∠OCF,
在△OAE和△OCF中,
∴△AOE≌△COF(ASA),
∴CF=AE,OE=OF,
∵AB=7,BC=5,OE=2,
∴EF=2OE=4,BE+CF=BE+AE=AB=7,
∴四边形BCFE的周长为:EF+BE+BC+CF=4+7+5=16.
[变式]在?ABCD中,对角线AC,BD交于点O,过点O作直线EF分别交线段AD,BC于点E,F.
(1)根据题意画出图形,并标上正确的字母.
(2)求证:DE=BF.
【解析】(1)作图如图:
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,OB=OD,
∴∠EDO=∠FBO,
在△DOE和△BOF中
∴△DOE≌△BOF.∴DE=BF.
