2017-2018学年八年级数学下册第18章平行四边形18.2.1矩形(第1课时)课时提升作业(含解析)(新版)新人教版
文档属性
| 名称 | 2017-2018学年八年级数学下册第18章平行四边形18.2.1矩形(第1课时)课时提升作业(含解析)(新版)新人教版 |  | |
| 格式 | zip | ||
| 文件大小 | 228.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-21 18:42:03 | ||
图片预览


文档简介
矩形
(第1课时)
(30分钟 50分)
一、选择题(每小题4分,共12分)
1.(2017·绍兴中考)在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图,该图中,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA.若∠ACB=21°,则∠ECD的度数是 ( )
A.7° B.21° C.23° D.24°
【解析】选C.∵∠ACB=21°,∴∠BAC=69°,
∵∠AFC是△AEF的外角,∴∠AFC=∠E+∠FAE,
∵∠E=∠FAE,∴∠ACF=∠AFC=2∠E,
∵∠BAC是△AEC的外角,∴∠BAC=∠E+∠ACF=3∠E=69°,则∠E=23°,
∵BE∥CD,∴∠ECD=∠E=23°.
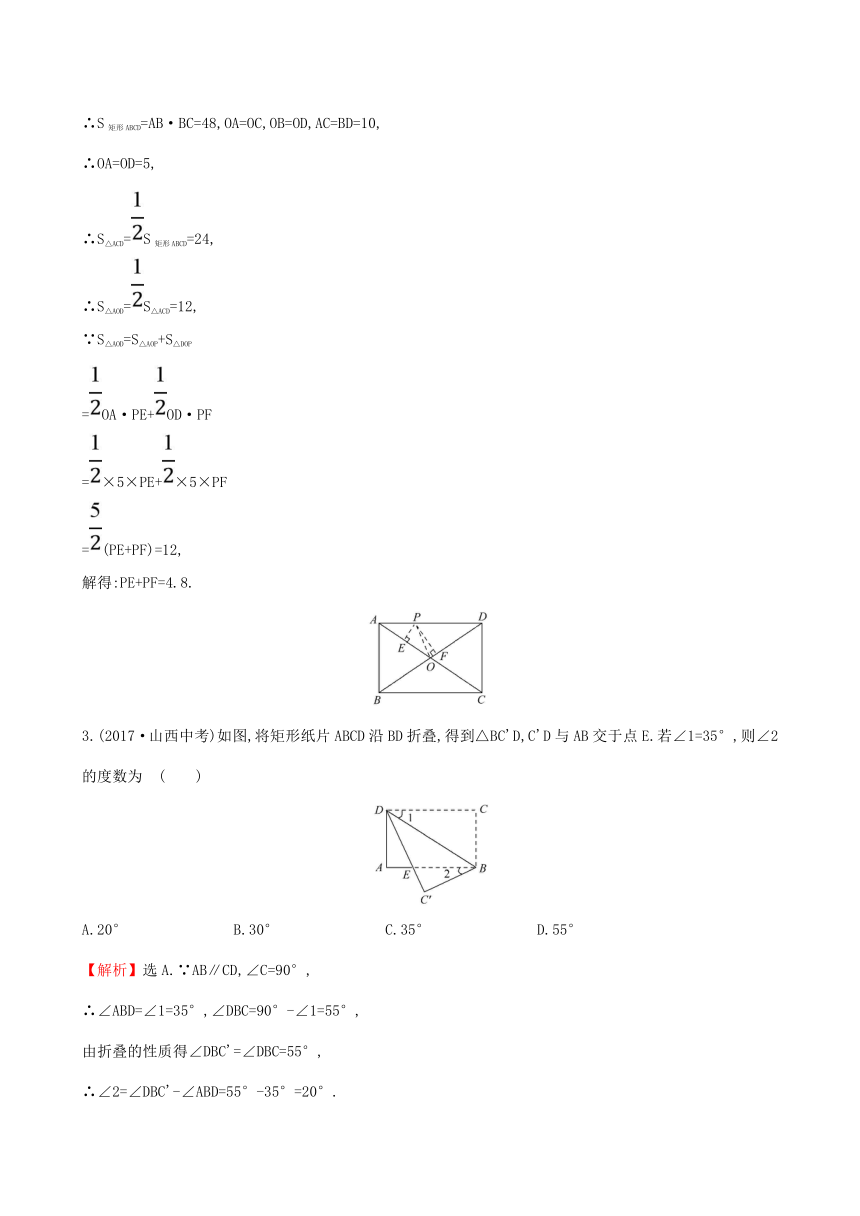
2.如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是 ( )
A.4.8 B.5 C.6 D.7.2
【解析】选A.连接OP,过点P作PE⊥AC于点E,作PF⊥BD于点F,
∵矩形的两条边AB,BC的长分别为6和8,
∴S矩形ABCD=AB·BC=48,OA=OC,OB=OD,AC=BD=10,
∴OA=OD=5,
∴S△ACD=S矩形ABCD=24,
∴S△AOD=S△ACD=12,
∵S△AOD=S△AOP+S△DOP
=OA·PE+OD·PF
=×5×PE+×5×PF
=(PE+PF)=12,
解得:PE+PF=4.8.
3.(2017·山西中考)如图,将矩形纸片ABCD沿BD折叠,得到△BC'D,C'D与AB交于点E.若∠1=35°,则∠2的度数为 ( )
A.20° B.30° C.35° D.55°
【解析】选A.∵AB∥CD,∠C=90°,
∴∠ABD=∠1=35°,∠DBC=90°-∠1=55°,
由折叠的性质得∠DBC'=∠DBC=55°,
∴∠2=∠DBC'-∠ABD=55°-35°=20°.
二、填空题(每小题4分,共12分)
4.如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE.如果∠ADB=30°,则∠E=______度.
【解析】
如图,连接AC,根据矩形的性质得:∠ADB=∠ACB=30°,∵AC=BD=CE,
∴△ACE为等腰三角形,
∠E=∠EAC=∠ACB=15°.
答案:15
5.(2017·宁夏中考)在△ABC中,AB=6,点D是AB的中点,过点D作DE∥BC,交AC于点E,点M在DE上,且ME=DM.当AM⊥BM时,则BC的长为__________.
【解析】∵AM⊥BM,点D是AB的中点,
∴DM=AB=3,
∵ME=DM,
∴ME=1,
∴DE=DM+ME=4,
∵点D是AB的中点,DE∥BC,
∴BC=2DE=8.
答案:8
6.如图,在矩形ABCD中,点E,F分别在边CD,BC上,且DC=3DE=3a,将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP=________.
【解析】∵DC=3DE=3a,
∴DE=a,EC=2a.
根据折叠的性质,EC=EP=2a,∠PEF=∠CEF,∠EPF=∠C=90°.
根据矩形的性质,∠D=90°,
在Rt△DPE中,EP=2DE=2a,
∴∠DPE=30°,∠DEP=60°.
∴∠PEF=∠CEF=(180°-60°)=60°.
∴在Rt△EPF中,∠PFE=30°.
∴EF=2EP=4a,
在Rt△EPF中,∠EPF=90°,EP=2a,EF=4a,
根据勾股定理,得FP==2a.
答案:2a
【变式训练】已知:如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=
120°,则∠AEO的度数是________.
【解析】∵四边形ABCD是矩形,
∠AOD=120°,
∴OA=OB,∠AOB=60°,
∴△AOB是等边三角形.
又∵AE平分∠BAD,∴∠BAE=45°,
∴BE=AB=OB,∠EAO=15°,
∴∠BOE=(180°-30°)÷2=75°,
∴∠AEO=180°-15°-60°-75°=30°.
答案:30°
三、解答题(共26分)
7.(12分)如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC,AD分别交于P,Q两点.
(1)求证:CP=AQ.
(2)若BP=1,PQ=2,∠AEF=45°,求矩形ABCD的面积.
【解析】(1)∵四边形ABCD是矩形,
∴∠A=∠ABC=∠C=∠ADC=90°,AB=CD,AD=BC,AB∥CD,AD∥BC,
∴∠E=∠F,
∵BE=DF,∴AE=CF,
在△CFP和△AEQ中,,
∴△CFP≌△AEQ(ASA),∴CP=AQ.
(2)∵AD∥BC,∴∠PBE=∠A=90°.
∵∠AEF=45°,∴△BEP、△AEQ是等腰直角三角形,
∴BE=BP=1,AQ=AE,
∴PE=BP=,
∴EQ=PE+PQ=+2=3,
∴AQ=AE=3,∴AB=AE-BE=2.
∵CP=AQ,AD=BC,∴DQ=BP=1,
∴AD=AQ+DQ=3+1=4,
∴矩形ABCD的面积=AB·AD=2×4=8.
【培优训练】
8.(14分)如图,在△ABC中,已知点D,E,F分别是AB,BC,CA的中点,AH是高.
(1)若BC=10,AH=8,求四边形ADEF的面积.
(2)求证:∠DHF=∠DEF.
【解析】(1)∵BC=10,AH=8,
∴S△ABC=×8×10=40,
∵点D,E,F分别是AB,BC,CA的中点,
∴△BDE,△EFC的面积都等于△ABC面积的,
∴四边形ADEF的面积=40-20=20.
(2)∵D,E,F分别是△ABC各边中点,
∴DE∥AC,EF∥AB,
∴四边形ADEF是平行四边形,∴∠DEF=∠DAF,
∵AH是△ABC的高,
∴△ABH,△ACH是直角三角形,
∵点D、点F是斜边AB,AC的中点,
∴DH=DA,HF=AF,
∴∠DAH=∠DHA,∠FAH=∠FHA,
∴∠DAH+∠FAH=∠FHA+∠DHA,
即∠DAF=∠DHF,∴∠DEF=∠DHF.
(第1课时)
(30分钟 50分)
一、选择题(每小题4分,共12分)
1.(2017·绍兴中考)在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图,该图中,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA.若∠ACB=21°,则∠ECD的度数是 ( )
A.7° B.21° C.23° D.24°
【解析】选C.∵∠ACB=21°,∴∠BAC=69°,
∵∠AFC是△AEF的外角,∴∠AFC=∠E+∠FAE,
∵∠E=∠FAE,∴∠ACF=∠AFC=2∠E,
∵∠BAC是△AEC的外角,∴∠BAC=∠E+∠ACF=3∠E=69°,则∠E=23°,
∵BE∥CD,∴∠ECD=∠E=23°.
2.如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是 ( )
A.4.8 B.5 C.6 D.7.2
【解析】选A.连接OP,过点P作PE⊥AC于点E,作PF⊥BD于点F,
∵矩形的两条边AB,BC的长分别为6和8,
∴S矩形ABCD=AB·BC=48,OA=OC,OB=OD,AC=BD=10,
∴OA=OD=5,
∴S△ACD=S矩形ABCD=24,
∴S△AOD=S△ACD=12,
∵S△AOD=S△AOP+S△DOP
=OA·PE+OD·PF
=×5×PE+×5×PF
=(PE+PF)=12,
解得:PE+PF=4.8.
3.(2017·山西中考)如图,将矩形纸片ABCD沿BD折叠,得到△BC'D,C'D与AB交于点E.若∠1=35°,则∠2的度数为 ( )
A.20° B.30° C.35° D.55°
【解析】选A.∵AB∥CD,∠C=90°,
∴∠ABD=∠1=35°,∠DBC=90°-∠1=55°,
由折叠的性质得∠DBC'=∠DBC=55°,
∴∠2=∠DBC'-∠ABD=55°-35°=20°.
二、填空题(每小题4分,共12分)
4.如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE.如果∠ADB=30°,则∠E=______度.
【解析】
如图,连接AC,根据矩形的性质得:∠ADB=∠ACB=30°,∵AC=BD=CE,
∴△ACE为等腰三角形,
∠E=∠EAC=∠ACB=15°.
答案:15
5.(2017·宁夏中考)在△ABC中,AB=6,点D是AB的中点,过点D作DE∥BC,交AC于点E,点M在DE上,且ME=DM.当AM⊥BM时,则BC的长为__________.
【解析】∵AM⊥BM,点D是AB的中点,
∴DM=AB=3,
∵ME=DM,
∴ME=1,
∴DE=DM+ME=4,
∵点D是AB的中点,DE∥BC,
∴BC=2DE=8.
答案:8
6.如图,在矩形ABCD中,点E,F分别在边CD,BC上,且DC=3DE=3a,将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP=________.
【解析】∵DC=3DE=3a,
∴DE=a,EC=2a.
根据折叠的性质,EC=EP=2a,∠PEF=∠CEF,∠EPF=∠C=90°.
根据矩形的性质,∠D=90°,
在Rt△DPE中,EP=2DE=2a,
∴∠DPE=30°,∠DEP=60°.
∴∠PEF=∠CEF=(180°-60°)=60°.
∴在Rt△EPF中,∠PFE=30°.
∴EF=2EP=4a,
在Rt△EPF中,∠EPF=90°,EP=2a,EF=4a,
根据勾股定理,得FP==2a.
答案:2a
【变式训练】已知:如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=
120°,则∠AEO的度数是________.
【解析】∵四边形ABCD是矩形,
∠AOD=120°,
∴OA=OB,∠AOB=60°,
∴△AOB是等边三角形.
又∵AE平分∠BAD,∴∠BAE=45°,
∴BE=AB=OB,∠EAO=15°,
∴∠BOE=(180°-30°)÷2=75°,
∴∠AEO=180°-15°-60°-75°=30°.
答案:30°
三、解答题(共26分)
7.(12分)如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC,AD分别交于P,Q两点.
(1)求证:CP=AQ.
(2)若BP=1,PQ=2,∠AEF=45°,求矩形ABCD的面积.
【解析】(1)∵四边形ABCD是矩形,
∴∠A=∠ABC=∠C=∠ADC=90°,AB=CD,AD=BC,AB∥CD,AD∥BC,
∴∠E=∠F,
∵BE=DF,∴AE=CF,
在△CFP和△AEQ中,,
∴△CFP≌△AEQ(ASA),∴CP=AQ.
(2)∵AD∥BC,∴∠PBE=∠A=90°.
∵∠AEF=45°,∴△BEP、△AEQ是等腰直角三角形,
∴BE=BP=1,AQ=AE,
∴PE=BP=,
∴EQ=PE+PQ=+2=3,
∴AQ=AE=3,∴AB=AE-BE=2.
∵CP=AQ,AD=BC,∴DQ=BP=1,
∴AD=AQ+DQ=3+1=4,
∴矩形ABCD的面积=AB·AD=2×4=8.
【培优训练】
8.(14分)如图,在△ABC中,已知点D,E,F分别是AB,BC,CA的中点,AH是高.
(1)若BC=10,AH=8,求四边形ADEF的面积.
(2)求证:∠DHF=∠DEF.
【解析】(1)∵BC=10,AH=8,
∴S△ABC=×8×10=40,
∵点D,E,F分别是AB,BC,CA的中点,
∴△BDE,△EFC的面积都等于△ABC面积的,
∴四边形ADEF的面积=40-20=20.
(2)∵D,E,F分别是△ABC各边中点,
∴DE∥AC,EF∥AB,
∴四边形ADEF是平行四边形,∴∠DEF=∠DAF,
∵AH是△ABC的高,
∴△ABH,△ACH是直角三角形,
∵点D、点F是斜边AB,AC的中点,
∴DH=DA,HF=AF,
∴∠DAH=∠DHA,∠FAH=∠FHA,
∴∠DAH+∠FAH=∠FHA+∠DHA,
即∠DAF=∠DHF,∴∠DEF=∠DHF.
