2017-2018学年八年级数学下册第18章平行四边形18.2.1矩形(第1课时)一课一练基础闯关(含解析)(新版)新人教版
文档属性
| 名称 | 2017-2018学年八年级数学下册第18章平行四边形18.2.1矩形(第1课时)一课一练基础闯关(含解析)(新版)新人教版 |  | |
| 格式 | zip | ||
| 文件大小 | 265.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-21 18:43:17 | ||
图片预览


文档简介
矩形
一课一练·基础闯关
题组矩形的性质
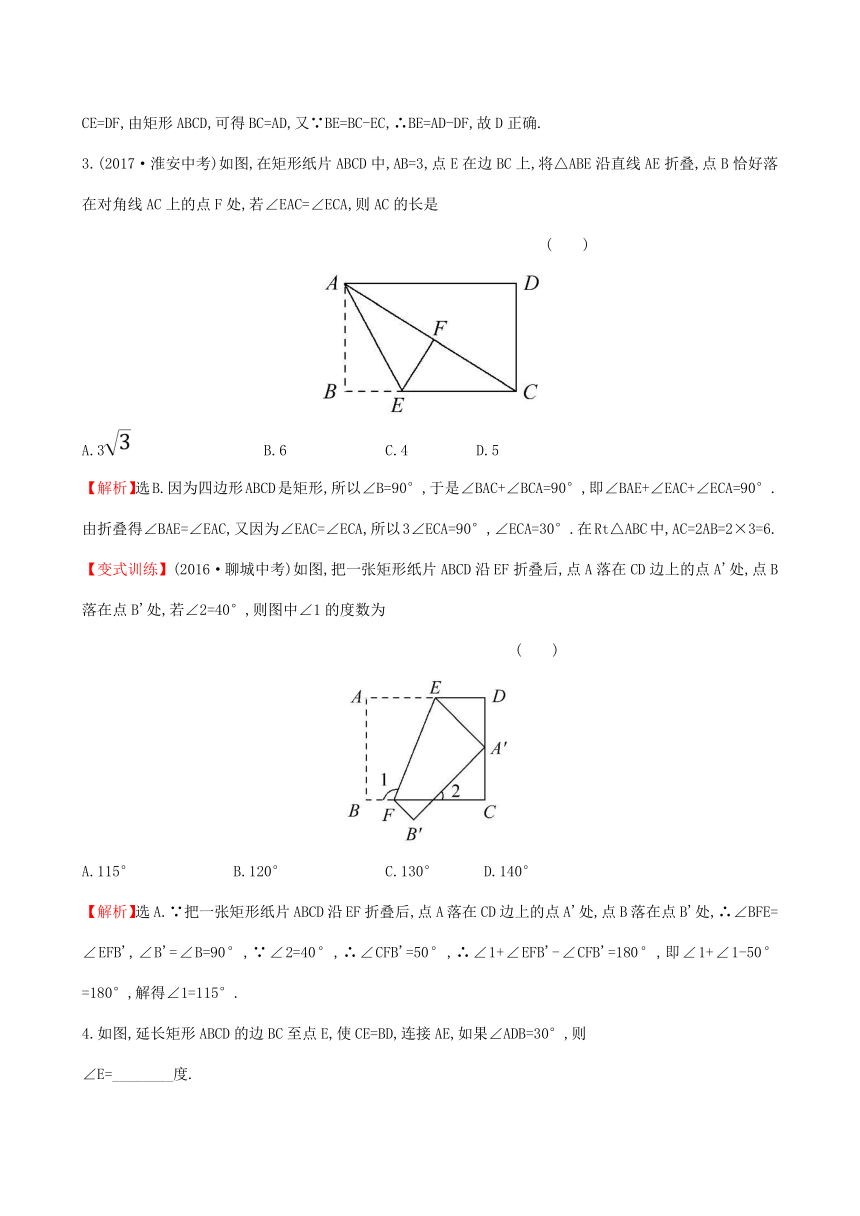
1.(教材变形题·P53练习T1)如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是 ( )
A.∠ABC=90° B.AC=BD
C.OA=OB D.OA=AD
【解析】选D.由矩形的四个角都是直角,可知∠ABC=90°,A正确;矩形的对角线相等且互相平分,所以AC=BD,OA=OB,B,C正确,无法判断OA与AD的大小关系,D错误.
2.如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是 ( )
A.△AFD≌△DCE B.AF=AD
C.AB=AF D.BE=AD-DF
【解析】选B.A.由矩形ABCD,AF⊥DE可得∠C=∠AFD=90°,AD∥BC,∴∠ADF=∠DEC.又∵DE=AD.∴△AFD≌△DCE(AAS).故A正确.B.∵∠ADF不一定等于30°,∴直角三角形ADF中,AF不一定等于AD的一半,故B错误.C.由△AFD≌△DCE,可得AF=CD,由矩形ABCD,可得AB=CD,∴AB=AF,故C正确.D.由△AFD≌△DCE,可得CE=DF,由矩形ABCD,可得BC=AD,又∵BE=BC-EC,∴BE=AD-DF,故D正确.
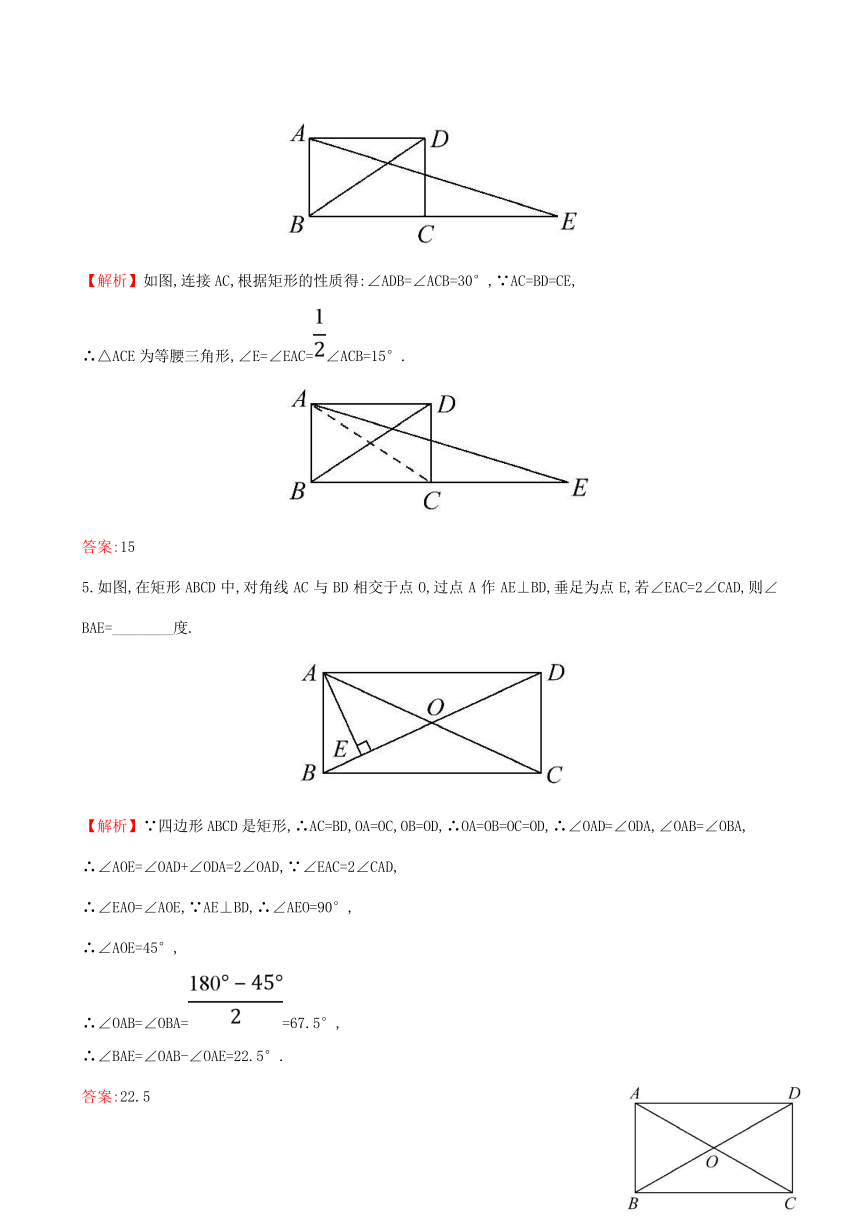
3.(2017·淮安中考)如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是
( )
A.3 B.6 C.4 D.5
【解析】选B.因为四边形ABCD是矩形,所以∠B=90°,于是∠BAC+∠BCA=90°,即∠BAE+∠EAC+∠ECA=90°.由折叠得∠BAE=∠EAC,又因为∠EAC=∠ECA,所以3∠ECA=90°,∠ECA=30°.在Rt△ABC中,AC=2AB=2×3=6.
【变式训练】(2016·聊城中考)如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A'处,点B落在点B'处,若∠2=40°,则图中∠1的度数为
( )
A.115° B.120° C.130° D.140°
【解析】选A.∵把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A'处,点B落在点B'处,∴∠BFE=∠EFB',∠B'=∠B=90°,∵∠2=40°,∴∠CFB'=50°,∴∠1+∠EFB'-∠CFB'=180°,即∠1+∠1-50°=180°,解得∠1=115°.
4.如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE,如果∠ADB=30°,则
∠E=________度.
【解析】如图,连接AC,根据矩形的性质得:∠ADB=∠ACB=30°,∵AC=BD=CE,
∴△ACE为等腰三角形,∠E=∠EAC=∠ACB=15°.
答案:15
5.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE=________度.
【解析】∵四边形ABCD是矩形,∴AC=BD,OA=OC,OB=OD,∴OA=OB=OC=OD,∴∠OAD=∠ODA,∠OAB=∠OBA,
∴∠AOE=∠OAD+∠ODA=2∠OAD,∵∠EAC=2∠CAD,
∴∠EAO=∠AOE,∵AE⊥BD,∴∠AEO=90°,
∴∠AOE=45°,
∴∠OAB=∠OBA==67.5°,
∴∠BAE=∠OAB-∠OAE=22.5°.
答案:22.5
6.如图,矩形ABCD的对角线AC,BD相交于点O,若AB=AO,求∠ABD的度数.
【解析】∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,∴AO=OB,
∵AB=AO,∴AB=AO=BO,
∴△ABO是等边三角形,
∴∠ABD=60°.
题组直角三角形斜边上中线的性质
1.(2017·大连中考)如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为 ( )
A.2a B.2a C.3a D.a
【解析】选B.∵CD⊥AB,CD=DE=a,∴CE=a,∵在△ABC中,∠ACB=90°,点E是AB的中点,∴AB=2CE=2a.
2.(2017·大庆中考)如图,△ABD是以BD为斜边的等腰直角三角形,在△BCD中,∠DBC=90°,∠BCD=60°,DC中点为E,AD与BE的延长线交于点F,则∠AFB的度数为 ( )
A.30° B.15° C.45° D.25°
【解题指南】根据直角三角形的性质得到BE=CE,求得∠CBE=60°,得到∠DBF=
30°,根据等腰直角三角形的性质得到∠ABD=45°,求得∠ABF=75°,根据三角形的内角和即可得到结论.
【解析】选B.∵∠DBC=90°,点E为DC中点,∴BE=CE,
∵∠BCD=60°,∴∠CBE=60°,∴∠DBF=30°,
∵△ABD是等腰直角三角形,∴∠ABD=45°,∴∠ABF=75°,
∴∠AFB=180°-90°-75°=15°.
3.(2017·淮安中考)如图,在Rt△ABC中,∠ACB=90°,点D,E分别是AB,AC的中点,点F是AD的中点,若AB=8,则EF=________.
【解析】因为在Rt△ABC中,∠ACB=90°,点D是AB的中点,所以CD=AB=×8=4.因为点E,F分别是AC,AD的中点,所以EF=CD=×4=2.
答案:2
4.如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连接EF交CD于点M,连接AM.
(1)求证:EF=AC.
(2)若∠BAC=45°,求线段AM,DM,BC之间的数量关系.
【解析】(1)∵CD=CB,点E为BD的中点,
∴CE⊥BD,
∵点F为AC的中点,
∴EF=AC.
(2)∵∠BAC=45°,CE⊥BD,
∴△AEC是等腰直角三角形,
∵点F为AC的中点,
∴EF垂直平分AC,
∴AM=CM,
∵CD=CM+DM=AM+DM,CD=CB,
∴BC=AM+DM.
如图,已知矩形ABCD中,F是BC上一点,且AF=BC,DE⊥AF,垂足是E,连接DF.
求证:(1)△ABF≌△DEA.
(2)DF是∠EDC的平分线.
【证明】(1)∵四边形ABCD是矩形,
∴∠B=90°,AD=BC,AD∥BC,
∴∠DAE=∠AFB,∵DE⊥AF,
∴∠DEA=∠B=90°.
∵AF=BC,∴AF=AD,
∴△ABF≌△DEA(AAS).
(2)由(1)知△ABF≌△DEA,∴DE=AB.
∵四边形ABCD是矩形,
∴∠C=90°,DC=AB.
∴DC=DE.
∵∠DEA=90°,∴∠DEF=∠C=90°.
∵DF=DF,∴△DCF≌△DEF,∴∠EDF=∠CDF.
∴DF是∠EDC的平分线.
【母题变式】在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.
求证:DF=DC.
【证明】连接DE.∵AD=AE,
∴∠AED=∠ADE.
∵四边形ABCD是矩形,
∴AD∥BC,∠C=90°.
∴∠ADE=∠DEC,
∴∠DEC=∠AED.
又∵DF⊥AE,
∴∠DFE=∠C=90°.
∵DE=DE,
∴△DFE≌△DCE.∴DF=DC.
[变式一]如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.求证:AF=BE.
【证明】∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BEA,
在△ABE和△DFA中,
∴△ABE≌△DFA(AAS),∴AF=BE.
[变式二]如图,在矩形ABCD中,BF=CE.求证:AE=DF.
【证明】∵四边形ABCD是矩形.
∴AB=CD,∠ABC=∠DCB.
∵BF=CE,∴BC-CE=BC-BF,即BE=FC.
∴△ABE≌△DCF(SAS),
∴AE=DF.
一课一练·基础闯关
题组矩形的性质
1.(教材变形题·P53练习T1)如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是 ( )
A.∠ABC=90° B.AC=BD
C.OA=OB D.OA=AD
【解析】选D.由矩形的四个角都是直角,可知∠ABC=90°,A正确;矩形的对角线相等且互相平分,所以AC=BD,OA=OB,B,C正确,无法判断OA与AD的大小关系,D错误.
2.如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是 ( )
A.△AFD≌△DCE B.AF=AD
C.AB=AF D.BE=AD-DF
【解析】选B.A.由矩形ABCD,AF⊥DE可得∠C=∠AFD=90°,AD∥BC,∴∠ADF=∠DEC.又∵DE=AD.∴△AFD≌△DCE(AAS).故A正确.B.∵∠ADF不一定等于30°,∴直角三角形ADF中,AF不一定等于AD的一半,故B错误.C.由△AFD≌△DCE,可得AF=CD,由矩形ABCD,可得AB=CD,∴AB=AF,故C正确.D.由△AFD≌△DCE,可得CE=DF,由矩形ABCD,可得BC=AD,又∵BE=BC-EC,∴BE=AD-DF,故D正确.
3.(2017·淮安中考)如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是
( )
A.3 B.6 C.4 D.5
【解析】选B.因为四边形ABCD是矩形,所以∠B=90°,于是∠BAC+∠BCA=90°,即∠BAE+∠EAC+∠ECA=90°.由折叠得∠BAE=∠EAC,又因为∠EAC=∠ECA,所以3∠ECA=90°,∠ECA=30°.在Rt△ABC中,AC=2AB=2×3=6.
【变式训练】(2016·聊城中考)如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A'处,点B落在点B'处,若∠2=40°,则图中∠1的度数为
( )
A.115° B.120° C.130° D.140°
【解析】选A.∵把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A'处,点B落在点B'处,∴∠BFE=∠EFB',∠B'=∠B=90°,∵∠2=40°,∴∠CFB'=50°,∴∠1+∠EFB'-∠CFB'=180°,即∠1+∠1-50°=180°,解得∠1=115°.
4.如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE,如果∠ADB=30°,则
∠E=________度.
【解析】如图,连接AC,根据矩形的性质得:∠ADB=∠ACB=30°,∵AC=BD=CE,
∴△ACE为等腰三角形,∠E=∠EAC=∠ACB=15°.
答案:15
5.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE=________度.
【解析】∵四边形ABCD是矩形,∴AC=BD,OA=OC,OB=OD,∴OA=OB=OC=OD,∴∠OAD=∠ODA,∠OAB=∠OBA,
∴∠AOE=∠OAD+∠ODA=2∠OAD,∵∠EAC=2∠CAD,
∴∠EAO=∠AOE,∵AE⊥BD,∴∠AEO=90°,
∴∠AOE=45°,
∴∠OAB=∠OBA==67.5°,
∴∠BAE=∠OAB-∠OAE=22.5°.
答案:22.5
6.如图,矩形ABCD的对角线AC,BD相交于点O,若AB=AO,求∠ABD的度数.
【解析】∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,∴AO=OB,
∵AB=AO,∴AB=AO=BO,
∴△ABO是等边三角形,
∴∠ABD=60°.
题组直角三角形斜边上中线的性质
1.(2017·大连中考)如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为 ( )
A.2a B.2a C.3a D.a
【解析】选B.∵CD⊥AB,CD=DE=a,∴CE=a,∵在△ABC中,∠ACB=90°,点E是AB的中点,∴AB=2CE=2a.
2.(2017·大庆中考)如图,△ABD是以BD为斜边的等腰直角三角形,在△BCD中,∠DBC=90°,∠BCD=60°,DC中点为E,AD与BE的延长线交于点F,则∠AFB的度数为 ( )
A.30° B.15° C.45° D.25°
【解题指南】根据直角三角形的性质得到BE=CE,求得∠CBE=60°,得到∠DBF=
30°,根据等腰直角三角形的性质得到∠ABD=45°,求得∠ABF=75°,根据三角形的内角和即可得到结论.
【解析】选B.∵∠DBC=90°,点E为DC中点,∴BE=CE,
∵∠BCD=60°,∴∠CBE=60°,∴∠DBF=30°,
∵△ABD是等腰直角三角形,∴∠ABD=45°,∴∠ABF=75°,
∴∠AFB=180°-90°-75°=15°.
3.(2017·淮安中考)如图,在Rt△ABC中,∠ACB=90°,点D,E分别是AB,AC的中点,点F是AD的中点,若AB=8,则EF=________.
【解析】因为在Rt△ABC中,∠ACB=90°,点D是AB的中点,所以CD=AB=×8=4.因为点E,F分别是AC,AD的中点,所以EF=CD=×4=2.
答案:2
4.如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连接EF交CD于点M,连接AM.
(1)求证:EF=AC.
(2)若∠BAC=45°,求线段AM,DM,BC之间的数量关系.
【解析】(1)∵CD=CB,点E为BD的中点,
∴CE⊥BD,
∵点F为AC的中点,
∴EF=AC.
(2)∵∠BAC=45°,CE⊥BD,
∴△AEC是等腰直角三角形,
∵点F为AC的中点,
∴EF垂直平分AC,
∴AM=CM,
∵CD=CM+DM=AM+DM,CD=CB,
∴BC=AM+DM.
如图,已知矩形ABCD中,F是BC上一点,且AF=BC,DE⊥AF,垂足是E,连接DF.
求证:(1)△ABF≌△DEA.
(2)DF是∠EDC的平分线.
【证明】(1)∵四边形ABCD是矩形,
∴∠B=90°,AD=BC,AD∥BC,
∴∠DAE=∠AFB,∵DE⊥AF,
∴∠DEA=∠B=90°.
∵AF=BC,∴AF=AD,
∴△ABF≌△DEA(AAS).
(2)由(1)知△ABF≌△DEA,∴DE=AB.
∵四边形ABCD是矩形,
∴∠C=90°,DC=AB.
∴DC=DE.
∵∠DEA=90°,∴∠DEF=∠C=90°.
∵DF=DF,∴△DCF≌△DEF,∴∠EDF=∠CDF.
∴DF是∠EDC的平分线.
【母题变式】在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.
求证:DF=DC.
【证明】连接DE.∵AD=AE,
∴∠AED=∠ADE.
∵四边形ABCD是矩形,
∴AD∥BC,∠C=90°.
∴∠ADE=∠DEC,
∴∠DEC=∠AED.
又∵DF⊥AE,
∴∠DFE=∠C=90°.
∵DE=DE,
∴△DFE≌△DCE.∴DF=DC.
[变式一]如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.求证:AF=BE.
【证明】∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BEA,
在△ABE和△DFA中,
∴△ABE≌△DFA(AAS),∴AF=BE.
[变式二]如图,在矩形ABCD中,BF=CE.求证:AE=DF.
【证明】∵四边形ABCD是矩形.
∴AB=CD,∠ABC=∠DCB.
∵BF=CE,∴BC-CE=BC-BF,即BE=FC.
∴△ABE≌△DCF(SAS),
∴AE=DF.
