2017-2018学年八年级数学下册第18章平行四边形18.2.3正方形课时提升作业(含解析)(新版)新人教版
文档属性
| 名称 | 2017-2018学年八年级数学下册第18章平行四边形18.2.3正方形课时提升作业(含解析)(新版)新人教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 276.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-21 18:55:20 | ||
图片预览



文档简介
正 方 形
(30分钟 50分)
一、选择题(每小题4分,共12分)
1.下列命题中,真命题是 ( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线互相垂直平分的四边形是正方形
【解析】选C.满足选项A或选项B中的条件时,不能推出四边形是平行四边形,因此它们都是假命题.由选项D中的条件只能推出四边形是菱形,因此也是假命题.只有选项C中的命题是真命题.
2.(2017·河南中考)我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D'处,则点C的对应点C'的坐标为 ( )
A.(,1) B.(2,1)
C.(1,) D.(2,)
【解析】选D.过点C'作C'E⊥x轴,垂足为E点,
∵AB=2,O是AB的中点,∴OA=OB=1,
在Rt△AOD'中,∵AD'=2,∴∠AD'O=30°,
∴∠D'AO=60°,
∵AD'∥BC',∴∠D'AO=∠C'BE=60°,
∴∠BC'E=30°,
∵BC'=2,∴BE=1,C'E=,∴EO=2,
∴C'的坐标为(2,).
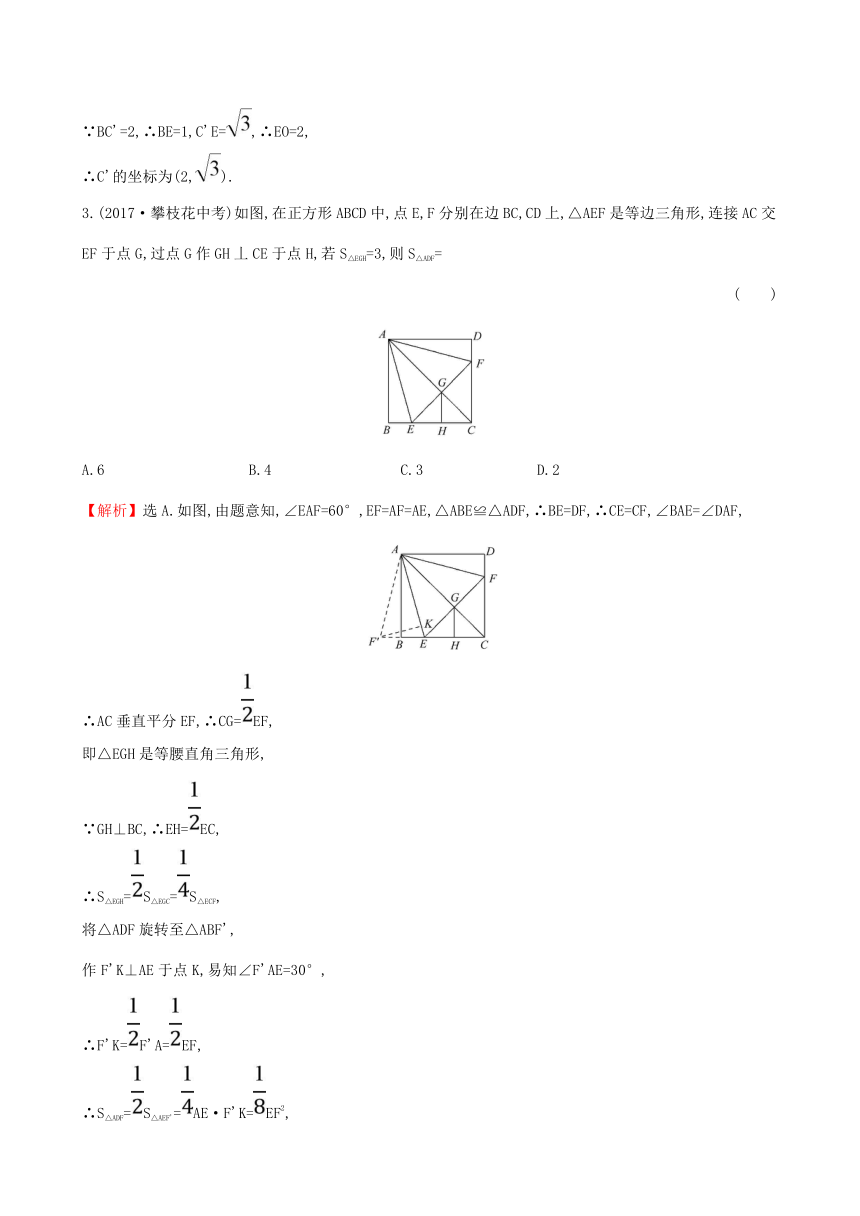
3.(2017·攀枝花中考)如图,在正方形ABCD中,点E,F分别在边BC,CD上,△AEF是等边三角形,连接AC交EF于点G,过点G作GH丄CE于点H,若S△EGH=3,则S△ADF=
( )
A.6 B.4 C.3 D.2
【解析】选A.如图,由题意知,∠EAF=60°,EF=AF=AE,△ABE≌△ADF,∴BE=DF,∴CE=CF,∠BAE=∠DAF,
∴AC垂直平分EF,∴CG=EF,
即△EGH是等腰直角三角形,
∵GH⊥BC,∴EH=EC,
∴S△EGH=S△EGC=S△ECF,
将△ADF旋转至△ABF',
作F'K⊥AE于点K,易知∠F'AE=30°,
∴F'K=F'A=EF,
∴S△ADF=S△AEF'=AE·F'K=EF2,
又S△ECF=EF·GC=EF2,
∴S△ADF=2S△EGH=6.
二、填空题(每小题4分,共12分)
4.(2017·天津中考)如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为________.
【解析】延长GE交AB于点O,作PH⊥OE于点H.
则PH∥AB.
∵P是AE的中点,∴PH是△AOE的中位线,
∴PH=OA=(3-1)=1.
在Rt△AOE中,OA=OE=2,
在Rt△PHE中,HE=PH=1.
∴HG=HE+EG=1+1=2.
∴在Rt△PHG中,PG===.
答案:
5.如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为__________.
【解题指南】首先由正方形的性质,得∠BAC=45°;再由等腰三角形的判定与性质,得EF=AF=3;然后由△EFC的周长为12,得到CF=9-EC;最后由勾股定理,得(9-EC)2+32=EC2,解之即可得到正确答案.
【解析】∵四边形ABCD是正方形,∴∠BAC=45°.
∵EF⊥AC,∴∠AEF=45°=∠BAC.∴EF=AF=3.
∵△EFC的周长为12,∴EF+CF+EC=12.
∴CF=9-EC.
在Rt△CEF中,由勾股定理,得(9-EC)2+32=EC2,解得EC=5.
答案:5
6.(2017·南充中考)如图,正方形ABCD和正方形CEFG的边长分别为a和b,正方形CEFG绕点C旋转.给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2.其中正确的结论是________(填写序号).
【解析】(1)
∵正方形的各边相等,各角都是90°,∴CB=CD,CE=CG,∠BCD=∠ECG=90°.∴∠BCD+∠DCE=∠ECG+∠DCE,即∠BCE=∠DCG.
∴△BCE≌△DCG(SAS).
∴BE=DG.可见结论①正确.
(2)如图,设BE交DC于点M,交DG于点O.由△BCE≌△DCG可知∠CBE=∠CDG,又∠BMC=∠DMO,∴∠DOB=∠DCB=90°,即BE⊥DG.可见结论②正确.(3)连接BD,EG.∵BE⊥DG,∴DE2+BG2=(OD2+OE2)+(OB2+OG2)=(OD2+OB2)+(OE2+OG2)=BD2+EG2.由勾股定理得BD2+EG2=2a2+2b2.
∴DE2+BG2=2a2+2b2.可见结论③正确.
答案:①②③
三、解答题(共26分)
7.(12分)(2017·青岛中考)已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF.
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.
【解题指南】(1)由菱形的性质得出∠B=∠D,AB=BC=DC=AD,由已知和三角形中位线定理证出AE=BE=DF=AF,OF=DC,OE=BC,OE∥BC,由SAS证明△BCE≌△DCF即可.
(2)由(1)得:AE=OE=OF=AF,证出四边形AEOF是菱形,再证出∠AEO=90°,即可得四边形AEOF是正方形.
【解析】(1)∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=DC=AD,
∵点E,O,F分别为AB,AC,AD的中点,
∴AE=BE=DF=AF,OF=DC,OE=BC,OE∥BC,在△BCE和△DCF中,
∴△BCE≌△DCF(SAS).
(2)当AB⊥BC时,四边形AEOF是正方形.理由如下:
由(1)得:AE=OE=OF=AF,
∴四边形AEOF是菱形,
∵AB⊥BC,OE∥BC,
∴OE⊥AB,
∴∠AEO=90°,
∴四边形AEOF是正方形.
【变式训练】如图,在正方形ABCD的外侧,作
等边三角形ADE,连接BE,CE.
(1)求证:BE=CE.
(2)求∠BEC的度数.
【解析】(1)∵四边形ABCD为正方形,
∴AB=AD=CD,∠BAD=∠ADC=90°,
∵三角形ADE为正三角形,
∴AE=AD=DE,∠EAD=∠EDA=60°.
∴∠BAE=∠CDE=150°,
在△BAE和△CDE中
∴△BAE≌△CDE,
∴BE=CE.
(2)∵AB=AD,AD=AE,
∴AB=AE,
∴∠ABE=∠AEB,
又∵∠BAE=150°,
∴∠ABE=∠AEB=15°,
同理:∠CED=15°,
∴∠BEC=60°-15°×2=30°.
【培优训练】
8.(14分)如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC的外角∠CAM的平分线,CE⊥AN,垂足为点E.
(1)求证:四边形ADCE为矩形.
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
【解析】(1)在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC.
∵AN是△ABC的外角∠CAM的平分线,
∴∠MAE=∠CAE.
∴∠DAE=∠DAC+∠CAE=×180°=90°.
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°.
∴四边形ADCE为矩形.
(2)例如,当∠BAC=90°时,四边形ADCE是正方形.
证明:∵∠BAC=90°,AB=AC,AD⊥BC于点D,
∴∠ACD=∠DAC=45°,
∴DC=AD.
由(1)四边形ADCE为矩形,
∴矩形ADCE是正方形.
【变式训练】如图,在正方形ABCD中,点M是对角线BD上的一点,过点M作ME∥CD交BC于点E,作MF∥BC交CD于点F.求证:AM=EF.
【证明】过点M作MP⊥AB交AB于点P,作MQ⊥AD交AD于点Q,
∵四边形ABCD是正方形,
∴四边形MFDQ和四边形PBEM是正方形,四边形APMQ是矩形,
∴AP=QM=DF=MF,PM=PB=ME,
∵在△APM和△FME中,
∴△APM≌△FME(SAS),
∴AM=EF.
(30分钟 50分)
一、选择题(每小题4分,共12分)
1.下列命题中,真命题是 ( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线互相垂直平分的四边形是正方形
【解析】选C.满足选项A或选项B中的条件时,不能推出四边形是平行四边形,因此它们都是假命题.由选项D中的条件只能推出四边形是菱形,因此也是假命题.只有选项C中的命题是真命题.
2.(2017·河南中考)我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D'处,则点C的对应点C'的坐标为 ( )
A.(,1) B.(2,1)
C.(1,) D.(2,)
【解析】选D.过点C'作C'E⊥x轴,垂足为E点,
∵AB=2,O是AB的中点,∴OA=OB=1,
在Rt△AOD'中,∵AD'=2,∴∠AD'O=30°,
∴∠D'AO=60°,
∵AD'∥BC',∴∠D'AO=∠C'BE=60°,
∴∠BC'E=30°,
∵BC'=2,∴BE=1,C'E=,∴EO=2,
∴C'的坐标为(2,).
3.(2017·攀枝花中考)如图,在正方形ABCD中,点E,F分别在边BC,CD上,△AEF是等边三角形,连接AC交EF于点G,过点G作GH丄CE于点H,若S△EGH=3,则S△ADF=
( )
A.6 B.4 C.3 D.2
【解析】选A.如图,由题意知,∠EAF=60°,EF=AF=AE,△ABE≌△ADF,∴BE=DF,∴CE=CF,∠BAE=∠DAF,
∴AC垂直平分EF,∴CG=EF,
即△EGH是等腰直角三角形,
∵GH⊥BC,∴EH=EC,
∴S△EGH=S△EGC=S△ECF,
将△ADF旋转至△ABF',
作F'K⊥AE于点K,易知∠F'AE=30°,
∴F'K=F'A=EF,
∴S△ADF=S△AEF'=AE·F'K=EF2,
又S△ECF=EF·GC=EF2,
∴S△ADF=2S△EGH=6.
二、填空题(每小题4分,共12分)
4.(2017·天津中考)如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为________.
【解析】延长GE交AB于点O,作PH⊥OE于点H.
则PH∥AB.
∵P是AE的中点,∴PH是△AOE的中位线,
∴PH=OA=(3-1)=1.
在Rt△AOE中,OA=OE=2,
在Rt△PHE中,HE=PH=1.
∴HG=HE+EG=1+1=2.
∴在Rt△PHG中,PG===.
答案:
5.如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为__________.
【解题指南】首先由正方形的性质,得∠BAC=45°;再由等腰三角形的判定与性质,得EF=AF=3;然后由△EFC的周长为12,得到CF=9-EC;最后由勾股定理,得(9-EC)2+32=EC2,解之即可得到正确答案.
【解析】∵四边形ABCD是正方形,∴∠BAC=45°.
∵EF⊥AC,∴∠AEF=45°=∠BAC.∴EF=AF=3.
∵△EFC的周长为12,∴EF+CF+EC=12.
∴CF=9-EC.
在Rt△CEF中,由勾股定理,得(9-EC)2+32=EC2,解得EC=5.
答案:5
6.(2017·南充中考)如图,正方形ABCD和正方形CEFG的边长分别为a和b,正方形CEFG绕点C旋转.给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2.其中正确的结论是________(填写序号).
【解析】(1)
∵正方形的各边相等,各角都是90°,∴CB=CD,CE=CG,∠BCD=∠ECG=90°.∴∠BCD+∠DCE=∠ECG+∠DCE,即∠BCE=∠DCG.
∴△BCE≌△DCG(SAS).
∴BE=DG.可见结论①正确.
(2)如图,设BE交DC于点M,交DG于点O.由△BCE≌△DCG可知∠CBE=∠CDG,又∠BMC=∠DMO,∴∠DOB=∠DCB=90°,即BE⊥DG.可见结论②正确.(3)连接BD,EG.∵BE⊥DG,∴DE2+BG2=(OD2+OE2)+(OB2+OG2)=(OD2+OB2)+(OE2+OG2)=BD2+EG2.由勾股定理得BD2+EG2=2a2+2b2.
∴DE2+BG2=2a2+2b2.可见结论③正确.
答案:①②③
三、解答题(共26分)
7.(12分)(2017·青岛中考)已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF.
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.
【解题指南】(1)由菱形的性质得出∠B=∠D,AB=BC=DC=AD,由已知和三角形中位线定理证出AE=BE=DF=AF,OF=DC,OE=BC,OE∥BC,由SAS证明△BCE≌△DCF即可.
(2)由(1)得:AE=OE=OF=AF,证出四边形AEOF是菱形,再证出∠AEO=90°,即可得四边形AEOF是正方形.
【解析】(1)∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=DC=AD,
∵点E,O,F分别为AB,AC,AD的中点,
∴AE=BE=DF=AF,OF=DC,OE=BC,OE∥BC,在△BCE和△DCF中,
∴△BCE≌△DCF(SAS).
(2)当AB⊥BC时,四边形AEOF是正方形.理由如下:
由(1)得:AE=OE=OF=AF,
∴四边形AEOF是菱形,
∵AB⊥BC,OE∥BC,
∴OE⊥AB,
∴∠AEO=90°,
∴四边形AEOF是正方形.
【变式训练】如图,在正方形ABCD的外侧,作
等边三角形ADE,连接BE,CE.
(1)求证:BE=CE.
(2)求∠BEC的度数.
【解析】(1)∵四边形ABCD为正方形,
∴AB=AD=CD,∠BAD=∠ADC=90°,
∵三角形ADE为正三角形,
∴AE=AD=DE,∠EAD=∠EDA=60°.
∴∠BAE=∠CDE=150°,
在△BAE和△CDE中
∴△BAE≌△CDE,
∴BE=CE.
(2)∵AB=AD,AD=AE,
∴AB=AE,
∴∠ABE=∠AEB,
又∵∠BAE=150°,
∴∠ABE=∠AEB=15°,
同理:∠CED=15°,
∴∠BEC=60°-15°×2=30°.
【培优训练】
8.(14分)如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC的外角∠CAM的平分线,CE⊥AN,垂足为点E.
(1)求证:四边形ADCE为矩形.
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
【解析】(1)在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC.
∵AN是△ABC的外角∠CAM的平分线,
∴∠MAE=∠CAE.
∴∠DAE=∠DAC+∠CAE=×180°=90°.
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°.
∴四边形ADCE为矩形.
(2)例如,当∠BAC=90°时,四边形ADCE是正方形.
证明:∵∠BAC=90°,AB=AC,AD⊥BC于点D,
∴∠ACD=∠DAC=45°,
∴DC=AD.
由(1)四边形ADCE为矩形,
∴矩形ADCE是正方形.
【变式训练】如图,在正方形ABCD中,点M是对角线BD上的一点,过点M作ME∥CD交BC于点E,作MF∥BC交CD于点F.求证:AM=EF.
【证明】过点M作MP⊥AB交AB于点P,作MQ⊥AD交AD于点Q,
∵四边形ABCD是正方形,
∴四边形MFDQ和四边形PBEM是正方形,四边形APMQ是矩形,
∴AP=QM=DF=MF,PM=PB=ME,
∵在△APM和△FME中,
∴△APM≌△FME(SAS),
∴AM=EF.
