2017-2018学年河南省商丘市拓城县八年级下第一次段考数学试卷含答案解析
文档属性
| 名称 | 2017-2018学年河南省商丘市拓城县八年级下第一次段考数学试卷含答案解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 221.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-21 00:00:00 | ||
图片预览




文档简介
2017-2018学年河南省商丘市拓城县八年级(下)第一次段考数学试卷
一、选择题(共9小题,每小题3分,满分27分)
1.(3分)一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则斜边的长为( )
A.4 B.6 C.8 D.10
2.(3分)下列说法中不正确的是( )
A.三个角度之比为3:4:5的三角形是直角三角形
B.三边之比为3:4:5的三角形是直角三角形
C.三个角度之比为1:2:3的三角形是直角三角形
D.三边之比为1:2:的三角形是直角三角形
3.(3分)若=3﹣b,则b的值为( )
A.0 B.0或1 C.b≤3 D.b≥3
4.(3分)下列计算中,正确的是( )
A. B. C. D.
5.(3分)化简(﹣2)2002 (+2)2003的结果为( )
A.﹣1 B.﹣2 C. +2 D.﹣﹣2
6.(3分)已知a、b、c是三角形的三边长,如果满足(a﹣6)2+=0,则三角形的形状是( )
A.底与腰不相等的等腰三角形 B.等边三角形
C.钝角三角形 D.直角三角形
7.(3分)等边三角形的边长为2,则该三角形的面积为( )
A.4 B. C.2 D.3
8.(3分)一艘轮船以16海里∕小时的速度从港口A出发向东北方向航行,同时另一轮船以12海里∕小时从港口A出发向东南方向航行,离开港口3小时后,则两船相距( )
A.36海里 B.48海里 C.60海里 D.84海里
9.(3分)化简的结果为( )
A. B. C. D.
二、填空(每题3分,计21分)
10.(3分)如果梯子的底端离建筑物9米,那么15米长的梯子可以到达建筑物的高度是 米.
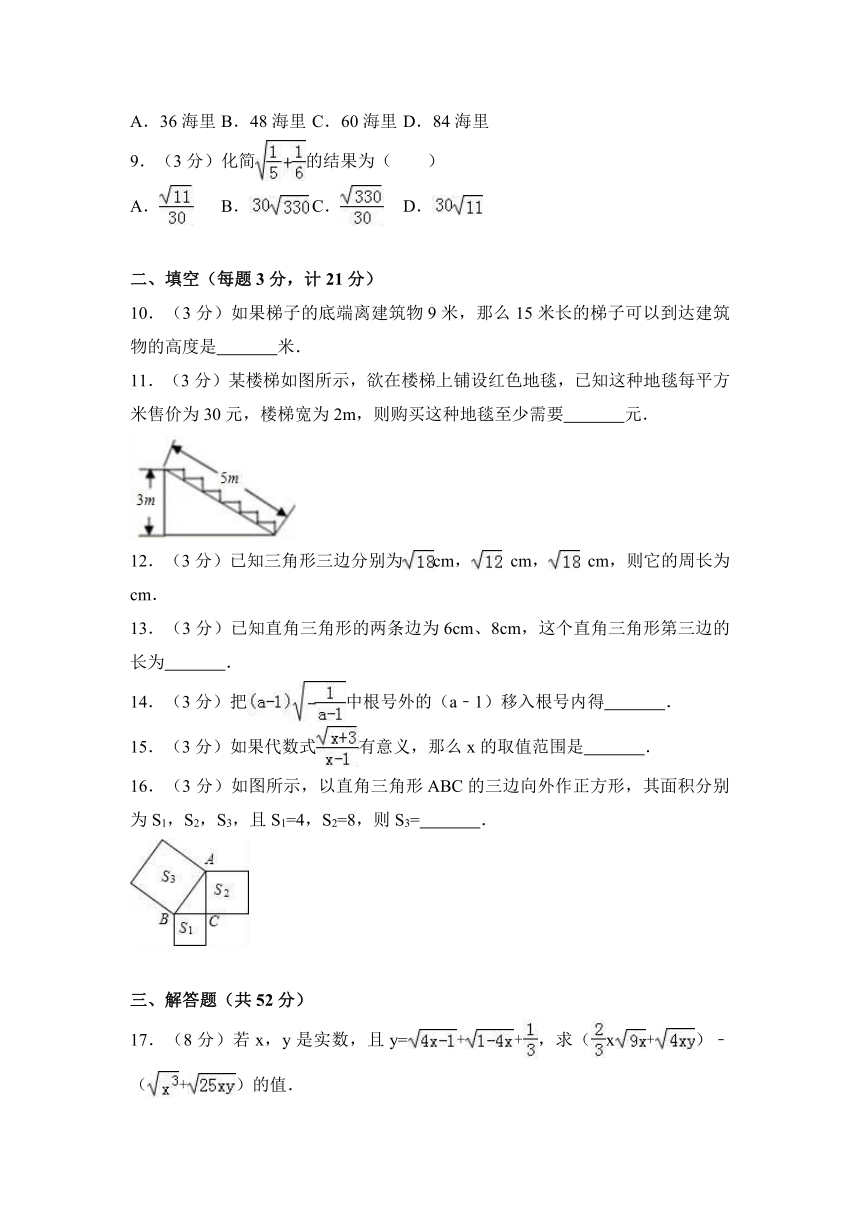
11.(3分)某楼梯如图所示,欲在楼梯上铺设红色地毯,已知这种地毯每平方米售价为30元,楼梯宽为2m,则购买这种地毯至少需要 元.
12.(3分)已知三角形三边分别为cm, cm, cm,则它的周长为 cm.
13.(3分)已知直角三角形的两条边为6cm、8cm,这个直角三角形第三边的长为 .
14.(3分)把中根号外的(a﹣1)移入根号内得 .
15.(3分)如果代数式有意义,那么x的取值范围是 .
16.(3分)如图所示,以直角三角形ABC的三边向外作正方形,其面积分别为S1,S2,S3,且S1=4,S2=8,则S3= .
三、解答题(共52分)
17.(8分)若x,y是实数,且y=++,求(x+)﹣(+)的值.
18.(8分)已知:,,求代数式x2﹣xy+y2值.
19.(8分)已知+b2﹣4b+4=0,求边长为a,b的等腰三角形的周长.
20.(9分)如图,在△DEF中,DE=17,FE=30,FE边上的中线DG=8,问△DEF是等腰三角形吗?为什么?
21.(9分)先化简再求﹣的值,其中a=.
22.(10分)如图,矩形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm,当沿AE折叠时,顶点D落在BC边上的点F处,试求CE的长.
参考答案与试题解析
一、选择题(共9小题,每小题3分,满分27分)
1.(3分)一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则斜边的长为( )
A.4 B.6 C.8 D.10
【解答】解:另一条直角边为a,则斜边为(a+2).
∵另一直角边长为6,
∴(a+2)2=a2+62,解得a=8,
∴a+2=8+2=10.
故选:D.
2.(3分)下列说法中不正确的是( )
A.三个角度之比为3:4:5的三角形是直角三角形
B.三边之比为3:4:5的三角形是直角三角形
C.三个角度之比为1:2:3的三角形是直角三角形
D.三边之比为1:2:的三角形是直角三角形
【解答】解:A不正确,因为根据三角形内角和定理求得各角的度数,其中没有直角;
B正确,因为其三边符合勾股定理的逆定理;
C正确,根据内角和公式求得三角的度数,有直角;
D正确,因为其三边符合勾股定理的逆定理;
故选:A.
3.(3分)若=3﹣b,则b的值为( )
A.0 B.0或1 C.b≤3 D.b≥3
【解答】解: ==|b﹣3|=3﹣b,
∴3﹣b≥0,
∴b≤3,
故选:C.
4.(3分)下列计算中,正确的是( )
A. B. C. D.
【解答】解:A,B,C都不是同类二次根式,不能合并,故错误;
D、3﹣=(3﹣)=,正确.
故选:D.
5.(3分)化简(﹣2)2002 (+2)2003的结果为( )
A.﹣1 B.﹣2 C. +2 D.﹣﹣2
【解答】解:原式=(﹣2)2002 (+2)2002 (+2)
=[(﹣2) (+2)]2002 (+2)
=1×(+2)
=+2,
故选:C.
6.(3分)已知a、b、c是三角形的三边长,如果满足(a﹣6)2+=0,则三角形的形状是( )
A.底与腰不相等的等腰三角形 B.等边三角形
C.钝角三角形 D.直角三角形
【解答】解:∵(a﹣6)2≥0,≥0,|c﹣10|≥0,
又∵(a﹣b)2+=0,
∴a﹣6=0,b﹣8=0,c﹣10=0,
解得:a=6,b=8,c=10,
∵62+82=36+64=100=102,
∴是直角三角形.
故选:D.
7.(3分)等边三角形的边长为2,则该三角形的面积为( )
A.4 B. C.2 D.3
【解答】解:∵等边三角形高线即中点,AB=2,
∴BD=CD=1,
在Rt△ABD中,AB=2,BD=1,
∴AD=,
∴S△ABC=BC AD=×2×=,
故选:B.
8.(3分)一艘轮船以16海里∕小时的速度从港口A出发向东北方向航行,同时另一轮船以12海里∕小时从港口A出发向东南方向航行,离开港口3小时后,则两船相距( )
A.36海里 B.48海里 C.60海里 D.84海里
【解答】解:∵两船行驶的方向是东北方向和东南方向,
∴∠BAC=90°,
两小时后,两艘船分别行驶了16×3=48,12×3=36海里,
根据勾股定理得: =60(海里).
故选:C.
9.(3分)化简的结果为( )
A. B. C. D.
【解答】解: ==,故选C.
二、填空(每题3分,计21分)
10.(3分)如果梯子的底端离建筑物9米,那么15米长的梯子可以到达建筑物的高度是 12 米.
【解答】解:∵直角三角形的斜边长为15m,一直角边长为9m,
∴另一直角边长==12m,
故梯子可到达建筑物的高度是12m.
故答案为:12.
11.(3分)某楼梯如图所示,欲在楼梯上铺设红色地毯,已知这种地毯每平方米售价为30元,楼梯宽为2m,则购买这种地毯至少需要 420 元.
【解答】解:已知直角三角形的一条直角边是3m,斜边是5m,
根据勾股定理得到:水平的直角边是4m,地毯水平的部分的和是水平边的长,竖直的部分的和是竖直边的长,
则购买这种地毯的长是3m+4m=7m,则面积是14m2,
价格是14×30=420元.
12.(3分)已知三角形三边分别为cm, cm, cm,则它的周长为 6 cm.
【解答】解:
=3+2+3
=6+2.
故答案为:6.
13.(3分)已知直角三角形的两条边为6cm、8cm,这个直角三角形第三边的长为 10cm或2cm .
【解答】解:当这个直角三角形的两直角边分别为6cm,8cm时,
则该三角形的斜边的长为=10cm;
当6cm为直角边,8cm为斜边时,则第三边长为=2
故答案为:10cm或2cm.
14.(3分)把中根号外的(a﹣1)移入根号内得 .
【解答】解:∵﹣>0,
∴a<1,
∴a﹣1<0,
∴=﹣(1﹣a)=﹣ =﹣=﹣.
故答案是:﹣
15.(3分)如果代数式有意义,那么x的取值范围是 x≥﹣3且x≠1 .
【解答】解:由题意得,x+3≥0且x﹣1≠0,
解得x≥﹣3且x≠1.
故答案为:x≥﹣3且x≠1.
16.(3分)如图所示,以直角三角形ABC的三边向外作正方形,其面积分别为S1,S2,S3,且S1=4,S2=8,则S3= 12 .
【解答】解:∵△ABC直角三角形,
∴BC2+AC2=AB2,
∵S1=BC2,S2=AC2,S3=AB2,S1=4,S2=8,
∴S3=S1+S2=12.
故答案为:12.
三、解答题(共52分)
17.(8分)若x,y是实数,且y=++,求(x+)﹣(+)的值.
【解答】解:依题意得:1=4x,
解得x=,
所以y=,
所以(x+)﹣(+)
=(××+)﹣(×+)
=+﹣﹣
=﹣.
18.(8分)已知:,,求代数式x2﹣xy+y2值.
【解答】解:x2﹣xy+y2=(x﹣y)2+xy,
当,,
原式=(2)2+7﹣5=22.
19.(8分)已知+b2﹣4b+4=0,求边长为a,b的等腰三角形的周长.
【解答】解:根据题意得,a﹣b﹣1=0,b﹣2=0,
解得a=3,b=2,
①若b=2是腰长,则底边为3,三角形的三边分别为2、2、3,
∵2+2>3,
∴能组成三角形,周长是2+2+3=7,
②若a=4是腰长,则底边为2,三角形的三边分别为2、4、4,
能组成三角形,
周长=2+4+4=10.
20.(9分)如图,在△DEF中,DE=17,FE=30,FE边上的中线DG=8,问△DEF是等腰三角形吗?为什么?
【解答】解:△DEF是等腰三角形,利用如下:
在△DGE中,DE=17,EG=FE=15,DG=8,
∵172=152+82,即DE2=EG2+DG2,
∴△DGE为直角三角形,且∠AGE=90°,即DG⊥EF.
又∵DG为EF边上的中线,
∴DE=DF,
∴△DEF是等腰三角形.
21.(9分)先化简再求﹣的值,其中a=.
【解答】解:当a==2﹣时,
∴a﹣1=1﹣<0
原式=﹣
=a﹣1+
=1﹣+2+
=3
22.(10分)如图,矩形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm,当沿AE折叠时,顶点D落在BC边上的点F处,试求CE的长.
【解答】解:∵四边形ABCD为矩形,
∴AD=BC=10,DC=AB=8,∠B=∠D=∠C=90°,
∵沿AE折叠时,顶点D落在BC边上的点F处,
∴AF=AD=10, DE=EF,
在Rt△ABF中,BF===6,
∴CF=BC﹣BF=10﹣6=4,
设CE=x,则DE=EF=8﹣x,
在Rt△CEF中,∵CF2+CE2=EF2,
∴42+x2=(8﹣x)2,解得x=5,
即CE的长为3.
一、选择题(共9小题,每小题3分,满分27分)
1.(3分)一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则斜边的长为( )
A.4 B.6 C.8 D.10
2.(3分)下列说法中不正确的是( )
A.三个角度之比为3:4:5的三角形是直角三角形
B.三边之比为3:4:5的三角形是直角三角形
C.三个角度之比为1:2:3的三角形是直角三角形
D.三边之比为1:2:的三角形是直角三角形
3.(3分)若=3﹣b,则b的值为( )
A.0 B.0或1 C.b≤3 D.b≥3
4.(3分)下列计算中,正确的是( )
A. B. C. D.
5.(3分)化简(﹣2)2002 (+2)2003的结果为( )
A.﹣1 B.﹣2 C. +2 D.﹣﹣2
6.(3分)已知a、b、c是三角形的三边长,如果满足(a﹣6)2+=0,则三角形的形状是( )
A.底与腰不相等的等腰三角形 B.等边三角形
C.钝角三角形 D.直角三角形
7.(3分)等边三角形的边长为2,则该三角形的面积为( )
A.4 B. C.2 D.3
8.(3分)一艘轮船以16海里∕小时的速度从港口A出发向东北方向航行,同时另一轮船以12海里∕小时从港口A出发向东南方向航行,离开港口3小时后,则两船相距( )
A.36海里 B.48海里 C.60海里 D.84海里
9.(3分)化简的结果为( )
A. B. C. D.
二、填空(每题3分,计21分)
10.(3分)如果梯子的底端离建筑物9米,那么15米长的梯子可以到达建筑物的高度是 米.
11.(3分)某楼梯如图所示,欲在楼梯上铺设红色地毯,已知这种地毯每平方米售价为30元,楼梯宽为2m,则购买这种地毯至少需要 元.
12.(3分)已知三角形三边分别为cm, cm, cm,则它的周长为 cm.
13.(3分)已知直角三角形的两条边为6cm、8cm,这个直角三角形第三边的长为 .
14.(3分)把中根号外的(a﹣1)移入根号内得 .
15.(3分)如果代数式有意义,那么x的取值范围是 .
16.(3分)如图所示,以直角三角形ABC的三边向外作正方形,其面积分别为S1,S2,S3,且S1=4,S2=8,则S3= .
三、解答题(共52分)
17.(8分)若x,y是实数,且y=++,求(x+)﹣(+)的值.
18.(8分)已知:,,求代数式x2﹣xy+y2值.
19.(8分)已知+b2﹣4b+4=0,求边长为a,b的等腰三角形的周长.
20.(9分)如图,在△DEF中,DE=17,FE=30,FE边上的中线DG=8,问△DEF是等腰三角形吗?为什么?
21.(9分)先化简再求﹣的值,其中a=.
22.(10分)如图,矩形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm,当沿AE折叠时,顶点D落在BC边上的点F处,试求CE的长.
参考答案与试题解析
一、选择题(共9小题,每小题3分,满分27分)
1.(3分)一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则斜边的长为( )
A.4 B.6 C.8 D.10
【解答】解:另一条直角边为a,则斜边为(a+2).
∵另一直角边长为6,
∴(a+2)2=a2+62,解得a=8,
∴a+2=8+2=10.
故选:D.
2.(3分)下列说法中不正确的是( )
A.三个角度之比为3:4:5的三角形是直角三角形
B.三边之比为3:4:5的三角形是直角三角形
C.三个角度之比为1:2:3的三角形是直角三角形
D.三边之比为1:2:的三角形是直角三角形
【解答】解:A不正确,因为根据三角形内角和定理求得各角的度数,其中没有直角;
B正确,因为其三边符合勾股定理的逆定理;
C正确,根据内角和公式求得三角的度数,有直角;
D正确,因为其三边符合勾股定理的逆定理;
故选:A.
3.(3分)若=3﹣b,则b的值为( )
A.0 B.0或1 C.b≤3 D.b≥3
【解答】解: ==|b﹣3|=3﹣b,
∴3﹣b≥0,
∴b≤3,
故选:C.
4.(3分)下列计算中,正确的是( )
A. B. C. D.
【解答】解:A,B,C都不是同类二次根式,不能合并,故错误;
D、3﹣=(3﹣)=,正确.
故选:D.
5.(3分)化简(﹣2)2002 (+2)2003的结果为( )
A.﹣1 B.﹣2 C. +2 D.﹣﹣2
【解答】解:原式=(﹣2)2002 (+2)2002 (+2)
=[(﹣2) (+2)]2002 (+2)
=1×(+2)
=+2,
故选:C.
6.(3分)已知a、b、c是三角形的三边长,如果满足(a﹣6)2+=0,则三角形的形状是( )
A.底与腰不相等的等腰三角形 B.等边三角形
C.钝角三角形 D.直角三角形
【解答】解:∵(a﹣6)2≥0,≥0,|c﹣10|≥0,
又∵(a﹣b)2+=0,
∴a﹣6=0,b﹣8=0,c﹣10=0,
解得:a=6,b=8,c=10,
∵62+82=36+64=100=102,
∴是直角三角形.
故选:D.
7.(3分)等边三角形的边长为2,则该三角形的面积为( )
A.4 B. C.2 D.3
【解答】解:∵等边三角形高线即中点,AB=2,
∴BD=CD=1,
在Rt△ABD中,AB=2,BD=1,
∴AD=,
∴S△ABC=BC AD=×2×=,
故选:B.
8.(3分)一艘轮船以16海里∕小时的速度从港口A出发向东北方向航行,同时另一轮船以12海里∕小时从港口A出发向东南方向航行,离开港口3小时后,则两船相距( )
A.36海里 B.48海里 C.60海里 D.84海里
【解答】解:∵两船行驶的方向是东北方向和东南方向,
∴∠BAC=90°,
两小时后,两艘船分别行驶了16×3=48,12×3=36海里,
根据勾股定理得: =60(海里).
故选:C.
9.(3分)化简的结果为( )
A. B. C. D.
【解答】解: ==,故选C.
二、填空(每题3分,计21分)
10.(3分)如果梯子的底端离建筑物9米,那么15米长的梯子可以到达建筑物的高度是 12 米.
【解答】解:∵直角三角形的斜边长为15m,一直角边长为9m,
∴另一直角边长==12m,
故梯子可到达建筑物的高度是12m.
故答案为:12.
11.(3分)某楼梯如图所示,欲在楼梯上铺设红色地毯,已知这种地毯每平方米售价为30元,楼梯宽为2m,则购买这种地毯至少需要 420 元.
【解答】解:已知直角三角形的一条直角边是3m,斜边是5m,
根据勾股定理得到:水平的直角边是4m,地毯水平的部分的和是水平边的长,竖直的部分的和是竖直边的长,
则购买这种地毯的长是3m+4m=7m,则面积是14m2,
价格是14×30=420元.
12.(3分)已知三角形三边分别为cm, cm, cm,则它的周长为 6 cm.
【解答】解:
=3+2+3
=6+2.
故答案为:6.
13.(3分)已知直角三角形的两条边为6cm、8cm,这个直角三角形第三边的长为 10cm或2cm .
【解答】解:当这个直角三角形的两直角边分别为6cm,8cm时,
则该三角形的斜边的长为=10cm;
当6cm为直角边,8cm为斜边时,则第三边长为=2
故答案为:10cm或2cm.
14.(3分)把中根号外的(a﹣1)移入根号内得 .
【解答】解:∵﹣>0,
∴a<1,
∴a﹣1<0,
∴=﹣(1﹣a)=﹣ =﹣=﹣.
故答案是:﹣
15.(3分)如果代数式有意义,那么x的取值范围是 x≥﹣3且x≠1 .
【解答】解:由题意得,x+3≥0且x﹣1≠0,
解得x≥﹣3且x≠1.
故答案为:x≥﹣3且x≠1.
16.(3分)如图所示,以直角三角形ABC的三边向外作正方形,其面积分别为S1,S2,S3,且S1=4,S2=8,则S3= 12 .
【解答】解:∵△ABC直角三角形,
∴BC2+AC2=AB2,
∵S1=BC2,S2=AC2,S3=AB2,S1=4,S2=8,
∴S3=S1+S2=12.
故答案为:12.
三、解答题(共52分)
17.(8分)若x,y是实数,且y=++,求(x+)﹣(+)的值.
【解答】解:依题意得:1=4x,
解得x=,
所以y=,
所以(x+)﹣(+)
=(××+)﹣(×+)
=+﹣﹣
=﹣.
18.(8分)已知:,,求代数式x2﹣xy+y2值.
【解答】解:x2﹣xy+y2=(x﹣y)2+xy,
当,,
原式=(2)2+7﹣5=22.
19.(8分)已知+b2﹣4b+4=0,求边长为a,b的等腰三角形的周长.
【解答】解:根据题意得,a﹣b﹣1=0,b﹣2=0,
解得a=3,b=2,
①若b=2是腰长,则底边为3,三角形的三边分别为2、2、3,
∵2+2>3,
∴能组成三角形,周长是2+2+3=7,
②若a=4是腰长,则底边为2,三角形的三边分别为2、4、4,
能组成三角形,
周长=2+4+4=10.
20.(9分)如图,在△DEF中,DE=17,FE=30,FE边上的中线DG=8,问△DEF是等腰三角形吗?为什么?
【解答】解:△DEF是等腰三角形,利用如下:
在△DGE中,DE=17,EG=FE=15,DG=8,
∵172=152+82,即DE2=EG2+DG2,
∴△DGE为直角三角形,且∠AGE=90°,即DG⊥EF.
又∵DG为EF边上的中线,
∴DE=DF,
∴△DEF是等腰三角形.
21.(9分)先化简再求﹣的值,其中a=.
【解答】解:当a==2﹣时,
∴a﹣1=1﹣<0
原式=﹣
=a﹣1+
=1﹣+2+
=3
22.(10分)如图,矩形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm,当沿AE折叠时,顶点D落在BC边上的点F处,试求CE的长.
【解答】解:∵四边形ABCD为矩形,
∴AD=BC=10,DC=AB=8,∠B=∠D=∠C=90°,
∵沿AE折叠时,顶点D落在BC边上的点F处,
∴AF=AD=10, DE=EF,
在Rt△ABF中,BF===6,
∴CF=BC﹣BF=10﹣6=4,
设CE=x,则DE=EF=8﹣x,
在Rt△CEF中,∵CF2+CE2=EF2,
∴42+x2=(8﹣x)2,解得x=5,
即CE的长为3.
同课章节目录
