安徽省滁州市定远县西片三校2017_2018学年高一数学4月月考试题
文档属性
| 名称 | 安徽省滁州市定远县西片三校2017_2018学年高一数学4月月考试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 240.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-22 00:00:00 | ||
图片预览



文档简介
安徽省滁州市定远县西片三校2017-2018学年高一数学4月月考试题
考生注意:
1、本卷满分150分,考试时间120分钟;
2、答题前请在答题卷上填写好自己的学校、姓名、班级、考号等信息;
3、请将答案正确填写在答题卷指定的位置,在非答题区位置作答无效。
第I卷(选择题 60分)
一、选择题(本大题共12小题,共60分)
1.给出以下数对序列:
(1,1);
(1,2)(2,1);
(1,3)(2,2)(3,1);
(1,4)(2,3)(3,2)(4,1);
…
记第i行的第j个数对为aij,如a43=(3,2),则anm=( )
A. (m,n-m+1) B. (m-1,n-m) C. (m-1,n-m+1) D. (m,n-m)
2.已知数列是公比为q的等比数列,且 , , 则的值为( ) A.3 B.2 C.3或-2 D.3或-3
3.在等比数列{an}中,a9+a10=a(a),a19+a20=b,则a99+a20的值为( ) A. B.()9 C. D.()10
4.若是所在平面内一点,且满足,则一定是( )
A.等边三角形 B.直角三角形
C.等腰三角形 D.等腰直角三角形
5.已知等差数列的前n项和为Sn,公差为d,若a1<0,S12=S6,下列说法正确的是( )
A. d<0 B. S19<0 C. 当n=9时Sn取最小值 D. S10>0
6.在等差数列{an}中,已知a3+a8>0,且S9<0,则S1、S2、…S9中最小的是( )
A.S4 B.S5 C.S6 D.S7
7.已知数列为等差数列,,,则( )
A. 4 B. 5 C. 6 D. 7
8.已知{}是等差数列,公差,且成等比数列,则等于
A. B. C. D.
9.在△ABC 中,已知A=30°,C=45°,a=2,则△ABC 的面积等于( )
A. B. C. D.
10.如图所示,已知两座灯塔A和B与海洋观察站C的距离都等于,灯塔A在观察站C的北偏东,灯塔B在观察站C的南偏东,则灯塔A与B灯塔B的距离为(?? )
A. B. C. D.
11.在中,角所对的边分别为,且,若,则的形状是( )
A. 等腰三角形 B. 直角三角形 C. 等边三角形 D. 等腰直角三角形
12.设的内角, , 的对边分别为, , .若, , ,且,则( )
A. B. C. D.
第II卷(非选择题 90分)
二、填空题(本大题共4小题,共20分)
13.已知中, 分别为内角的对边,且,则 .
14.中, 为线段的中点, , ,则________.
15.已知数列满足, ,则__________.
16.已知的三边长成公比为的等比数列,则最大的余弦值为__________.
三、解答题(本大题共6小题,共70分)
17.已知数列{an}的前n项和 , 求an .
18.在中,角的对边分别是,且.
(1)求角的大小;
(2)求的取值范围.
19.已知各项均为正数的数列,满足,().
(1)求数列的通项公式;
(2)求数列的前项和.
20.在中,内角的对边分别为,已知,.
(1)求的值;
(2)若,求的面积.
21.已知数列是公差不为零的等差数列,其前项和为,满足,且恰为等比数列的前三项.
(1)求数列,的通项公式;
(2)设是数列的前项和,是否存在,使得等式成立,若存在,求出的值;若不存在,说明理由.
22.如图1,在路边安装路灯,路宽为,灯柱长为米,灯杆长为1米,且灯杆与灯柱成角,路灯采用圆锥形灯罩,其轴截面的顶角为,灯罩轴线与灯杆垂直.
⑴设灯罩轴线与路面的交点为,若米,求灯柱长;
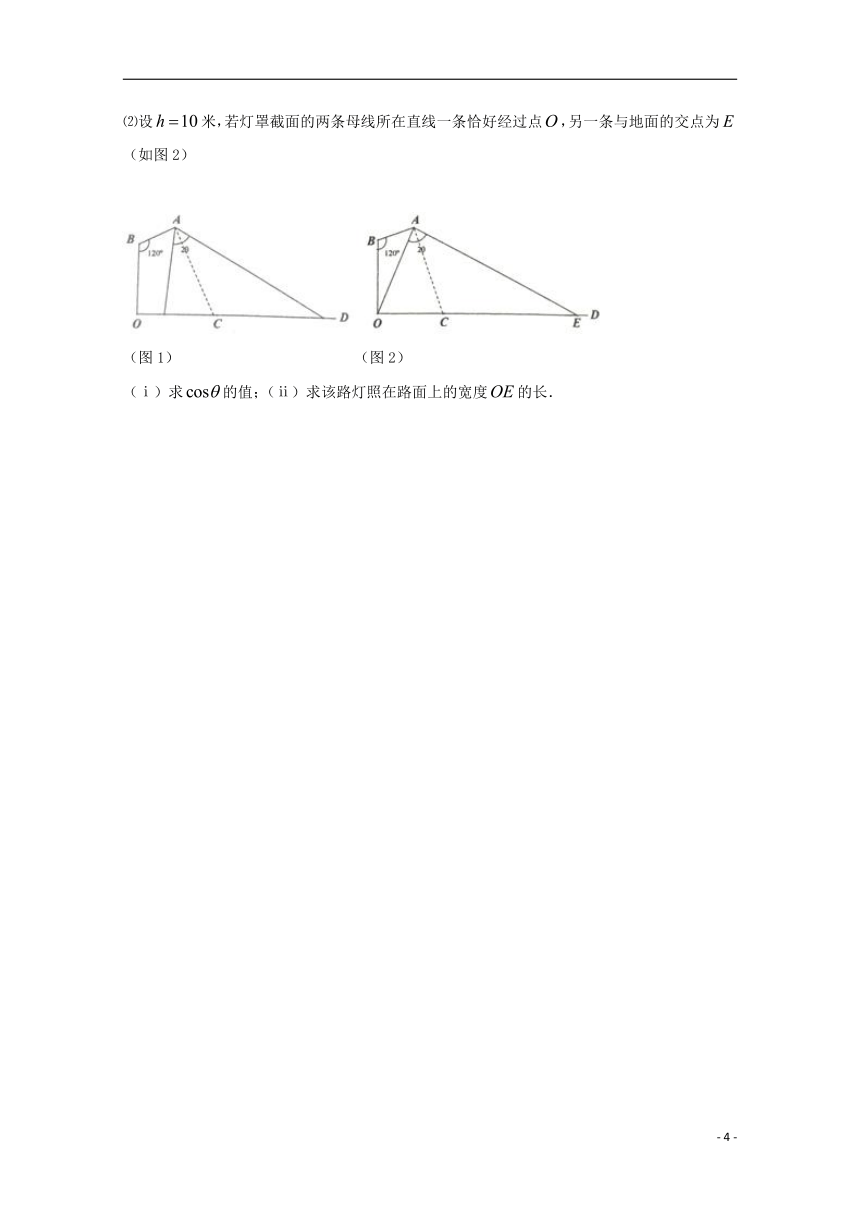
⑵设米,若灯罩截面的两条母线所在直线一条恰好经过点,另一条与地面的交点为(如图2)
(图1) (图2)
(ⅰ)求的值;(ⅱ)求该路灯照在路面上的宽度的长.
参考答案
1. A2.D3.A4.B5.C6.B7.B8.D9.B10.B11.C12.A
13.
14.
15.
16.
17.【解析】a1=S1=3+2=5, an=Sn﹣Sn﹣1=(3+2n)﹣(3+2n﹣1)=2n﹣1 , 当n=1时,2n﹣1=1≠a1 , ∴.
18.(1);(2).
【解析】(1)由正弦定理可得,,
从而可得,,
于是,又为三角形内角,因此,;
(2)
,
由可知,,所以,从而,
,故范围为.
19.(1)(2)
【解析】(1)因为,(),所以,
因为,所以().
(2)由(1)知,,所以,
所以,①
则,②
①②,得 ,
所以.
20.(1);(2).
【解析】(1)∵,,得.
又,
∴.
(2)由,得,,于是,
由及正弦定理,得,
设的面积为,则.
21.(1),;(2)不存在.
【解析】(1)设等差数列的公差为,所以
解得∴.
,∴.
(2),
,
因为,单调递减,得.
而,所以不存在,使得等式成立.
22.(1)灯柱长为13米.
(2)(ⅰ)值为;(ⅱ) 长为米.
【解析】
(1)过点作的垂线,垂足为,过点作的垂线,垂足为.
因为,
所以, ,
所以, ,
又因为,所以,
因为,所以,
解得.
(2)(ⅰ)在中,由余弦定理得
,所以,
在中,由正弦定理得,即,
解得,所以.
(ⅱ), ,
所以 ,
在中,由正弦定理得,即
.
答:(1)灯柱长为13米.
(2)(ⅰ)值为;(ⅱ) 长为米.
考生注意:
1、本卷满分150分,考试时间120分钟;
2、答题前请在答题卷上填写好自己的学校、姓名、班级、考号等信息;
3、请将答案正确填写在答题卷指定的位置,在非答题区位置作答无效。
第I卷(选择题 60分)
一、选择题(本大题共12小题,共60分)
1.给出以下数对序列:
(1,1);
(1,2)(2,1);
(1,3)(2,2)(3,1);
(1,4)(2,3)(3,2)(4,1);
…
记第i行的第j个数对为aij,如a43=(3,2),则anm=( )
A. (m,n-m+1) B. (m-1,n-m) C. (m-1,n-m+1) D. (m,n-m)
2.已知数列是公比为q的等比数列,且 , , 则的值为( ) A.3 B.2 C.3或-2 D.3或-3
3.在等比数列{an}中,a9+a10=a(a),a19+a20=b,则a99+a20的值为( ) A. B.()9 C. D.()10
4.若是所在平面内一点,且满足,则一定是( )
A.等边三角形 B.直角三角形
C.等腰三角形 D.等腰直角三角形
5.已知等差数列的前n项和为Sn,公差为d,若a1<0,S12=S6,下列说法正确的是( )
A. d<0 B. S19<0 C. 当n=9时Sn取最小值 D. S10>0
6.在等差数列{an}中,已知a3+a8>0,且S9<0,则S1、S2、…S9中最小的是( )
A.S4 B.S5 C.S6 D.S7
7.已知数列为等差数列,,,则( )
A. 4 B. 5 C. 6 D. 7
8.已知{}是等差数列,公差,且成等比数列,则等于
A. B. C. D.
9.在△ABC 中,已知A=30°,C=45°,a=2,则△ABC 的面积等于( )
A. B. C. D.
10.如图所示,已知两座灯塔A和B与海洋观察站C的距离都等于,灯塔A在观察站C的北偏东,灯塔B在观察站C的南偏东,则灯塔A与B灯塔B的距离为(?? )
A. B. C. D.
11.在中,角所对的边分别为,且,若,则的形状是( )
A. 等腰三角形 B. 直角三角形 C. 等边三角形 D. 等腰直角三角形
12.设的内角, , 的对边分别为, , .若, , ,且,则( )
A. B. C. D.
第II卷(非选择题 90分)
二、填空题(本大题共4小题,共20分)
13.已知中, 分别为内角的对边,且,则 .
14.中, 为线段的中点, , ,则________.
15.已知数列满足, ,则__________.
16.已知的三边长成公比为的等比数列,则最大的余弦值为__________.
三、解答题(本大题共6小题,共70分)
17.已知数列{an}的前n项和 , 求an .
18.在中,角的对边分别是,且.
(1)求角的大小;
(2)求的取值范围.
19.已知各项均为正数的数列,满足,().
(1)求数列的通项公式;
(2)求数列的前项和.
20.在中,内角的对边分别为,已知,.
(1)求的值;
(2)若,求的面积.
21.已知数列是公差不为零的等差数列,其前项和为,满足,且恰为等比数列的前三项.
(1)求数列,的通项公式;
(2)设是数列的前项和,是否存在,使得等式成立,若存在,求出的值;若不存在,说明理由.
22.如图1,在路边安装路灯,路宽为,灯柱长为米,灯杆长为1米,且灯杆与灯柱成角,路灯采用圆锥形灯罩,其轴截面的顶角为,灯罩轴线与灯杆垂直.
⑴设灯罩轴线与路面的交点为,若米,求灯柱长;
⑵设米,若灯罩截面的两条母线所在直线一条恰好经过点,另一条与地面的交点为(如图2)
(图1) (图2)
(ⅰ)求的值;(ⅱ)求该路灯照在路面上的宽度的长.
参考答案
1. A2.D3.A4.B5.C6.B7.B8.D9.B10.B11.C12.A
13.
14.
15.
16.
17.【解析】a1=S1=3+2=5, an=Sn﹣Sn﹣1=(3+2n)﹣(3+2n﹣1)=2n﹣1 , 当n=1时,2n﹣1=1≠a1 , ∴.
18.(1);(2).
【解析】(1)由正弦定理可得,,
从而可得,,
于是,又为三角形内角,因此,;
(2)
,
由可知,,所以,从而,
,故范围为.
19.(1)(2)
【解析】(1)因为,(),所以,
因为,所以().
(2)由(1)知,,所以,
所以,①
则,②
①②,得 ,
所以.
20.(1);(2).
【解析】(1)∵,,得.
又,
∴.
(2)由,得,,于是,
由及正弦定理,得,
设的面积为,则.
21.(1),;(2)不存在.
【解析】(1)设等差数列的公差为,所以
解得∴.
,∴.
(2),
,
因为,单调递减,得.
而,所以不存在,使得等式成立.
22.(1)灯柱长为13米.
(2)(ⅰ)值为;(ⅱ) 长为米.
【解析】
(1)过点作的垂线,垂足为,过点作的垂线,垂足为.
因为,
所以, ,
所以, ,
又因为,所以,
因为,所以,
解得.
(2)(ⅰ)在中,由余弦定理得
,所以,
在中,由正弦定理得,即,
解得,所以.
(ⅱ), ,
所以 ,
在中,由正弦定理得,即
.
答:(1)灯柱长为13米.
(2)(ⅰ)值为;(ⅱ) 长为米.
同课章节目录
