19.1.1变量与函数(第2课时) 课件
图片预览











文档简介
(共31张PPT)
1、掌握常量和变量、自变量和因变量(函数)基本概念;
2、了解表示函数关系的三种方法:解析法、列表法、图象法,并会用解析法表示数量关系。
学习重难点
重点 借助简单实例,了解常量与变量的意义;理解函数概念和自变量的意义。 难点 函数概念的理解。
1.什么叫变量?
2.什么叫常量?
复习回顾
小试身手
指出其中的变量与常量:
y=2x
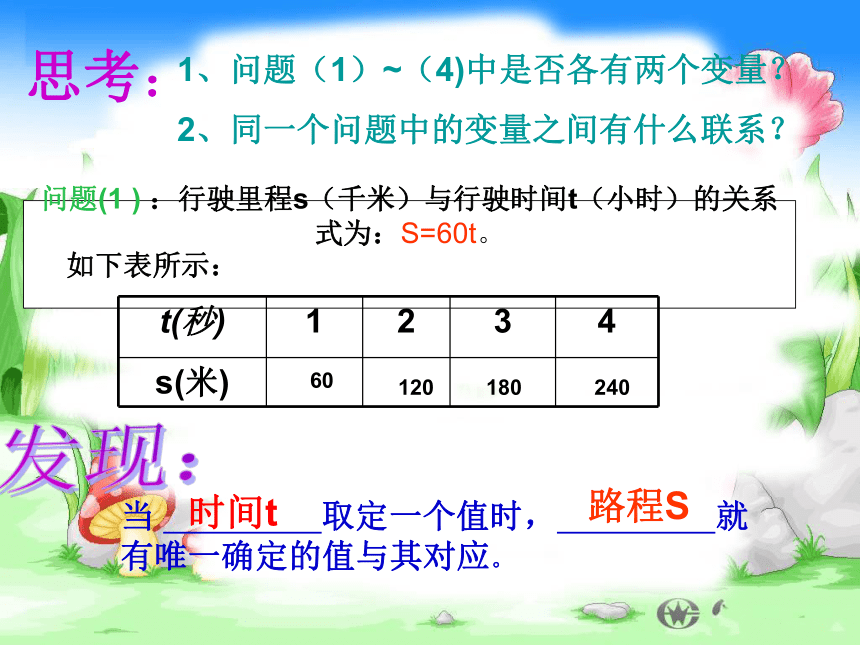
问题(1 ) :行驶里程s(千米)与行驶时间t(小时)的关系式为:S=60t。
当 取定一个值时, 就有唯一确定的值与其对应。
时间t
路程S
t(秒) 1 2 3 4
s(米)
1、问题(1)~(4)中是否各有两个变量?
2、同一个问题中的变量之间有什么联系?
60
120
240
180
思考:
如下表所示:
问题(2)
票房收入y元与售票数量x张的关系式:
y=10x
X=150时 y=1500;
X=205时 y=2050;
X=310时 y=3100;
当________取定一个值时,_______就有唯一确定的值与其对应。
售票数量x
票房收入y
问题(3)
圆的面积s与半径r的关系式为:
据此可以算出r分别为10cm,20cm,30cm时,s分别为
当 取定一个值时, 就有唯一确定的值与其对应。
圆的半径r
面积s
问题(4)
矩形的邻边长y与x的关系式为:y=5-x
据此可以算出x分别为3m,3.5m,4m,4.5m时,y分别为2m,1.5m,1m,0.5m.
当 取定一个值时, 就有唯一确定的值与其对应。
x
y
2 两个变量互相联系,当其中一个 变量取定一个值时,另一个变量就有(唯一确定的值与其对应)
1 每个变化的过程中都存在着(两个)变量.
函数的概念:
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值。
在一个变化过程中,
如果有两个变量x与y,
并且对于x的每一个确定的值,y都有唯 一确定的值与其对应,
那么我们就说x是自变量 ,
y是x的函数。
函数概念理解
(1)在一个变化过程中
(2)有两个变量x与y
(3)对于x的每一个确定的值,y都有唯 一确定的值与其对应
思考: 1 . S=60t; 2. y=10x ; 3.
4.y=5-x
上面每个问题中,哪个量是自变量?哪个量是自变量函数?
想一想
在计算器上按下列程序进行操作:
输入x(任意一个数)
按键
×
2
+
5
=
显示y(计算结果)
填表
x 1 3 - 4 0 101
y
显示的数y是x的函数吗?为什么?
7
11
- 3
5
207
收获心得
(自变量)
函数关系可以表述为:
输入x
函数关系
输出y
(因变量)
y的值是唯一的
下图是体检时的心电图.其中图上点的横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,对于x的每一个确定的值,y都有唯一确定的对应值吗?
o
x
y
思考(1)
思考(2)
像 1 . S=60t; 2. y=10x ; 3.
4.y=5-x
一.函数关系是用数学式子给出的 (叫解析式法)
二. 前面像体检心电图函数关系是用图象给出的 (叫图象法)
三 .前面我国人口数统计表函数关系是用表格给出的 (叫列表法)
例1 一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中的余油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km。
(1)写出表示y与x的函数关系的式子。
(2)指出自变量x的取值范围
(3)汽车行驶200 km时,油箱中还有多少油?
解:(1) 函数关系式为: y = 50-0.1x
(2) 由x≥0及50-0.1x ≥0 得 0 ≤ x ≤ 500
∴自变量的取值范围是: 0 ≤ x ≤ 500
(3)当 x = 200时,函数 y 的值为:y=50-0.1×200=30
因此,当汽车行驶200 km时,油箱中还有油30L
1、判断下列问题中的变量y是不是x的函数?
是
(1)在 y = 2x 中的y与x;
(2)在 y = x 中的y与x;
2
是
(3)在 y = x 中的y与x;
2
不是
自我挑战
对于x的每一个值,y总有唯一的值与它对应,y才是x的函数。
2.下列各式中,X是自变量,请判断Y是不是X的函数?若是,求出自变量X的取值范围。
3.y= +
1
x
4.y=
1.y= 2x
2.y=
解:1 y是x的函数。
2、y是x的函数。
∵X-3 ≥0∴x ≥3.
3、y不是x的函数。
4、y是x的函数. x≠0.
X为全体实数。
3.求出下列函数中自变量的取值范围
(1)
(2)
(3)
解: 由n-1≥0得n≥1 ∴自变量 n 的取值范围: n≥1
解:由x+2 ≠ 0得 x≠-2 ∴自变量 n 的取值范围: x≠-2
解:自变量的取值范围是: k≤1且k ≠-1
4.写出下列各问题中的关系式,并指出其中的自变量与函数。
(1)正方形的面积S 随边长 x 的变化
(2)秀水村的耕地面积是106m2,这个村人均耕地面积y随着人数x的变化而变化
S=x2
(3)长方形的周长是18 ,它的长是m,宽是n ;
m=9-n
5.下列关系中,y不是x函数的是( )
D
A
y=2x+15
X≥1且为整数
x ≠ -1
闯关题:
解:∵花盆图案形如三角形,每边花有n个,总共有3n个,
其中重复了算3个。
∴ s 与 n 的函数关系式为: s = 3n-3 (n>1的整数)
(2) 腰长AB=3时,底边的长.
(3) 自变量的取值范围;
(1) 关于 的函数解析式;
等腰三角形ABC的周长为10, 底边BC长为 , 腰AB长为 , 求:
智慧岛
通过这节课的学习,你有什么收获?
自变量的取值范围
确定自变量的取值范围时,不仅要考虑函数关系式有意义,而且还要注意问题的实际意义。
函数的概念
函数一语,起用于公元1692 年,最早见自德国数
学家莱布尼兹的著作。 他
是德国最重要的自然科学
家、数学家、物理学家、
历史学家和哲学家,一个
举世罕见的科学天才,和
牛顿同为微积分的创建人。
他博览群书,涉猎百科,对丰富人类的科学知识宝库做出了不可磨灭的贡献。
今日作业
P81
1,2
1、掌握常量和变量、自变量和因变量(函数)基本概念;
2、了解表示函数关系的三种方法:解析法、列表法、图象法,并会用解析法表示数量关系。
学习重难点
重点 借助简单实例,了解常量与变量的意义;理解函数概念和自变量的意义。 难点 函数概念的理解。
1.什么叫变量?
2.什么叫常量?
复习回顾
小试身手
指出其中的变量与常量:
y=2x
问题(1 ) :行驶里程s(千米)与行驶时间t(小时)的关系式为:S=60t。
当 取定一个值时, 就有唯一确定的值与其对应。
时间t
路程S
t(秒) 1 2 3 4
s(米)
1、问题(1)~(4)中是否各有两个变量?
2、同一个问题中的变量之间有什么联系?
60
120
240
180
思考:
如下表所示:
问题(2)
票房收入y元与售票数量x张的关系式:
y=10x
X=150时 y=1500;
X=205时 y=2050;
X=310时 y=3100;
当________取定一个值时,_______就有唯一确定的值与其对应。
售票数量x
票房收入y
问题(3)
圆的面积s与半径r的关系式为:
据此可以算出r分别为10cm,20cm,30cm时,s分别为
当 取定一个值时, 就有唯一确定的值与其对应。
圆的半径r
面积s
问题(4)
矩形的邻边长y与x的关系式为:y=5-x
据此可以算出x分别为3m,3.5m,4m,4.5m时,y分别为2m,1.5m,1m,0.5m.
当 取定一个值时, 就有唯一确定的值与其对应。
x
y
2 两个变量互相联系,当其中一个 变量取定一个值时,另一个变量就有(唯一确定的值与其对应)
1 每个变化的过程中都存在着(两个)变量.
函数的概念:
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值。
在一个变化过程中,
如果有两个变量x与y,
并且对于x的每一个确定的值,y都有唯 一确定的值与其对应,
那么我们就说x是自变量 ,
y是x的函数。
函数概念理解
(1)在一个变化过程中
(2)有两个变量x与y
(3)对于x的每一个确定的值,y都有唯 一确定的值与其对应
思考: 1 . S=60t; 2. y=10x ; 3.
4.y=5-x
上面每个问题中,哪个量是自变量?哪个量是自变量函数?
想一想
在计算器上按下列程序进行操作:
输入x(任意一个数)
按键
×
2
+
5
=
显示y(计算结果)
填表
x 1 3 - 4 0 101
y
显示的数y是x的函数吗?为什么?
7
11
- 3
5
207
收获心得
(自变量)
函数关系可以表述为:
输入x
函数关系
输出y
(因变量)
y的值是唯一的
下图是体检时的心电图.其中图上点的横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,对于x的每一个确定的值,y都有唯一确定的对应值吗?
o
x
y
思考(1)
思考(2)
像 1 . S=60t; 2. y=10x ; 3.
4.y=5-x
一.函数关系是用数学式子给出的 (叫解析式法)
二. 前面像体检心电图函数关系是用图象给出的 (叫图象法)
三 .前面我国人口数统计表函数关系是用表格给出的 (叫列表法)
例1 一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中的余油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km。
(1)写出表示y与x的函数关系的式子。
(2)指出自变量x的取值范围
(3)汽车行驶200 km时,油箱中还有多少油?
解:(1) 函数关系式为: y = 50-0.1x
(2) 由x≥0及50-0.1x ≥0 得 0 ≤ x ≤ 500
∴自变量的取值范围是: 0 ≤ x ≤ 500
(3)当 x = 200时,函数 y 的值为:y=50-0.1×200=30
因此,当汽车行驶200 km时,油箱中还有油30L
1、判断下列问题中的变量y是不是x的函数?
是
(1)在 y = 2x 中的y与x;
(2)在 y = x 中的y与x;
2
是
(3)在 y = x 中的y与x;
2
不是
自我挑战
对于x的每一个值,y总有唯一的值与它对应,y才是x的函数。
2.下列各式中,X是自变量,请判断Y是不是X的函数?若是,求出自变量X的取值范围。
3.y= +
1
x
4.y=
1.y= 2x
2.y=
解:1 y是x的函数。
2、y是x的函数。
∵X-3 ≥0∴x ≥3.
3、y不是x的函数。
4、y是x的函数. x≠0.
X为全体实数。
3.求出下列函数中自变量的取值范围
(1)
(2)
(3)
解: 由n-1≥0得n≥1 ∴自变量 n 的取值范围: n≥1
解:由x+2 ≠ 0得 x≠-2 ∴自变量 n 的取值范围: x≠-2
解:自变量的取值范围是: k≤1且k ≠-1
4.写出下列各问题中的关系式,并指出其中的自变量与函数。
(1)正方形的面积S 随边长 x 的变化
(2)秀水村的耕地面积是106m2,这个村人均耕地面积y随着人数x的变化而变化
S=x2
(3)长方形的周长是18 ,它的长是m,宽是n ;
m=9-n
5.下列关系中,y不是x函数的是( )
D
A
y=2x+15
X≥1且为整数
x ≠ -1
闯关题:
解:∵花盆图案形如三角形,每边花有n个,总共有3n个,
其中重复了算3个。
∴ s 与 n 的函数关系式为: s = 3n-3 (n>1的整数)
(2) 腰长AB=3时,底边的长.
(3) 自变量的取值范围;
(1) 关于 的函数解析式;
等腰三角形ABC的周长为10, 底边BC长为 , 腰AB长为 , 求:
智慧岛
通过这节课的学习,你有什么收获?
自变量的取值范围
确定自变量的取值范围时,不仅要考虑函数关系式有意义,而且还要注意问题的实际意义。
函数的概念
函数一语,起用于公元1692 年,最早见自德国数
学家莱布尼兹的著作。 他
是德国最重要的自然科学
家、数学家、物理学家、
历史学家和哲学家,一个
举世罕见的科学天才,和
牛顿同为微积分的创建人。
他博览群书,涉猎百科,对丰富人类的科学知识宝库做出了不可磨灭的贡献。
今日作业
P81
1,2
