9.1.1 认识三角形同步练习
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
9.1.1 认识三角形同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1. 由三条不在同一直线上的线段首尾顺次连结组成的平面图形叫三角形,这三条线段叫做三角形的边 . www-2-1-cnjy-com
2. 三角形中内角的一边与另一边的反向延长线所组成的角叫三角形的外角,在三角形的一个顶点处有两个外角,它们是一对对顶角 . 21*cnjy*com
3.三角形的分类
( http: / / www.21cnjy.com )
4. 三角形的三条中线、三条角平分线、三 ( http: / / www.21cnjy.com )条高(或所在的直线)都能交于一点 , 直角三角形三条高的交点就是直角顶点 ,钝角三角形有两条高位于三角形的外部.
基础知识和能力拓展精练
一.选择题(共9小题)
1.三角形按角分类可以分为( )
A.锐角三角形、直角三角形、钝角三角形
B.等腰三角形、等边三角形、不等边三角形
C.直角三角形、等边直角三角形
D.以上答案都不正确
2.如图,图中以AB为边的三角形的个数是( )
( http: / / www.21cnjy.com )
A.3 B.4 C.5 D.6
3.画△ABC中AB边上的高,下列画法中正确的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
4.至少有两边相等的三角形是( )
A.等边三角形 B.等腰三角形 C.等腰直角三角形 D.锐角三角形
5.如图,AD⊥BD于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )
( http: / / www.21cnjy.com )
A.△ABC中,AD是BC边上的高 B.△GBC中,CF是BG边上的高
C.△ABC中,GC是BC边上的高 D.△GBC中,GC是BC边上的高
6.如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
( http: / / www.21cnjy.com )
A.AB=2BF B.∠ACE= ( http: / / www.21cnjy.com )∠ACB C.AE=BE D.CD⊥BE
7.下面说法错误的是( )
A.三角形的三条角平分线交于一点
B.三角形的三条中线交于一点
C.三角形的三条高交于一点
D.三角形的三条高所在的直线交于一点
8.下列说法正确的是( )
①三角形的三条中线都在三角形内部;②三角形的三条角平分线都在三角形内部;③三角形三条高都在三角形的内部.【来源:21cnj*y.co*m】
A.①②③ B.①② C.②③ D.①③
9.三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
二.填空题(共7小题)
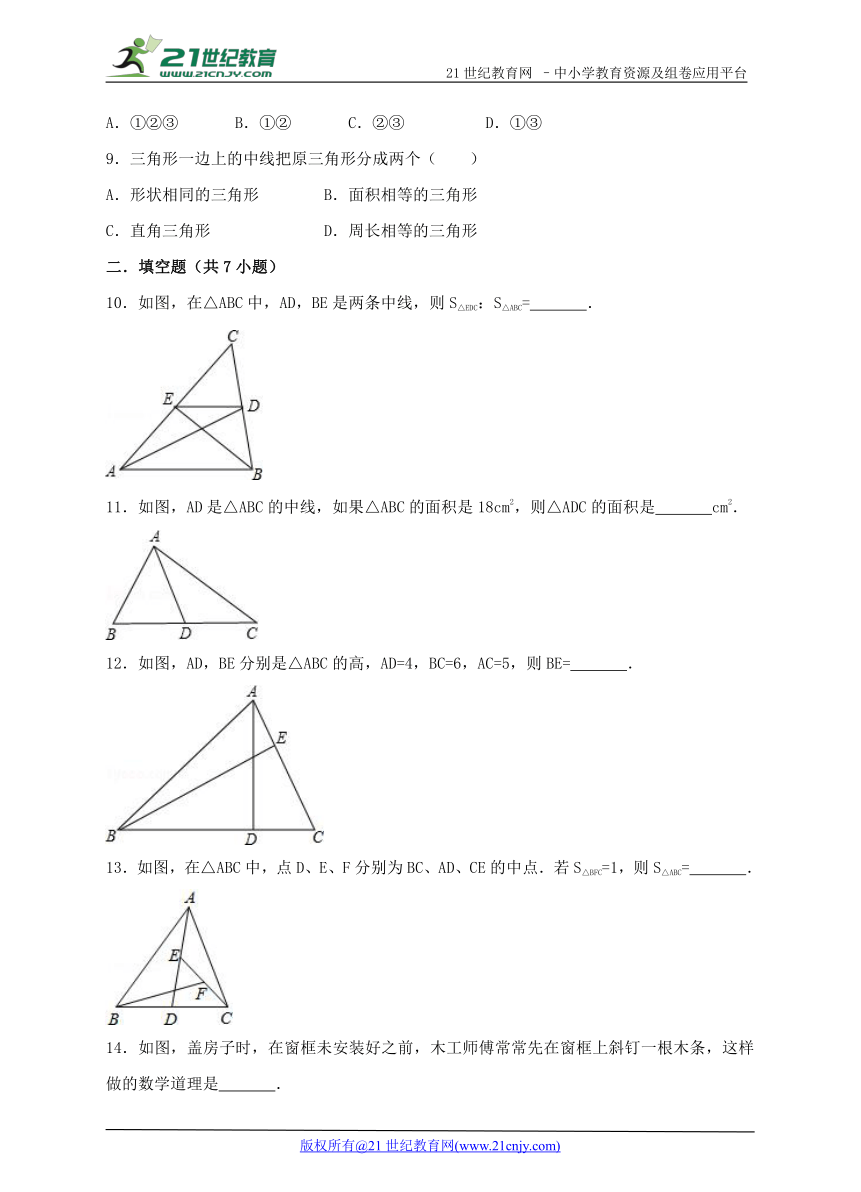
10.如图,在△ABC中,AD,BE是两条中线,则S△EDC:S△ABC= .
( http: / / www.21cnjy.com )
11.如图,AD是△ABC的中线,如果△ABC的面积是18cm2,则△ADC的面积是 cm2.
( http: / / www.21cnjy.com )
12.如图,AD,BE分别是△ABC的高,AD=4,BC=6,AC=5,则BE= .
( http: / / www.21cnjy.com )
13.如图,在△ABC中,点D、E、F分别为BC、AD、CE的中点.若S△BFC=1,则S△ABC= .
( http: / / www.21cnjy.com )
14.如图,盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,这样做的数学道理是 .21·cn·jy·com
( http: / / www.21cnjy.com )
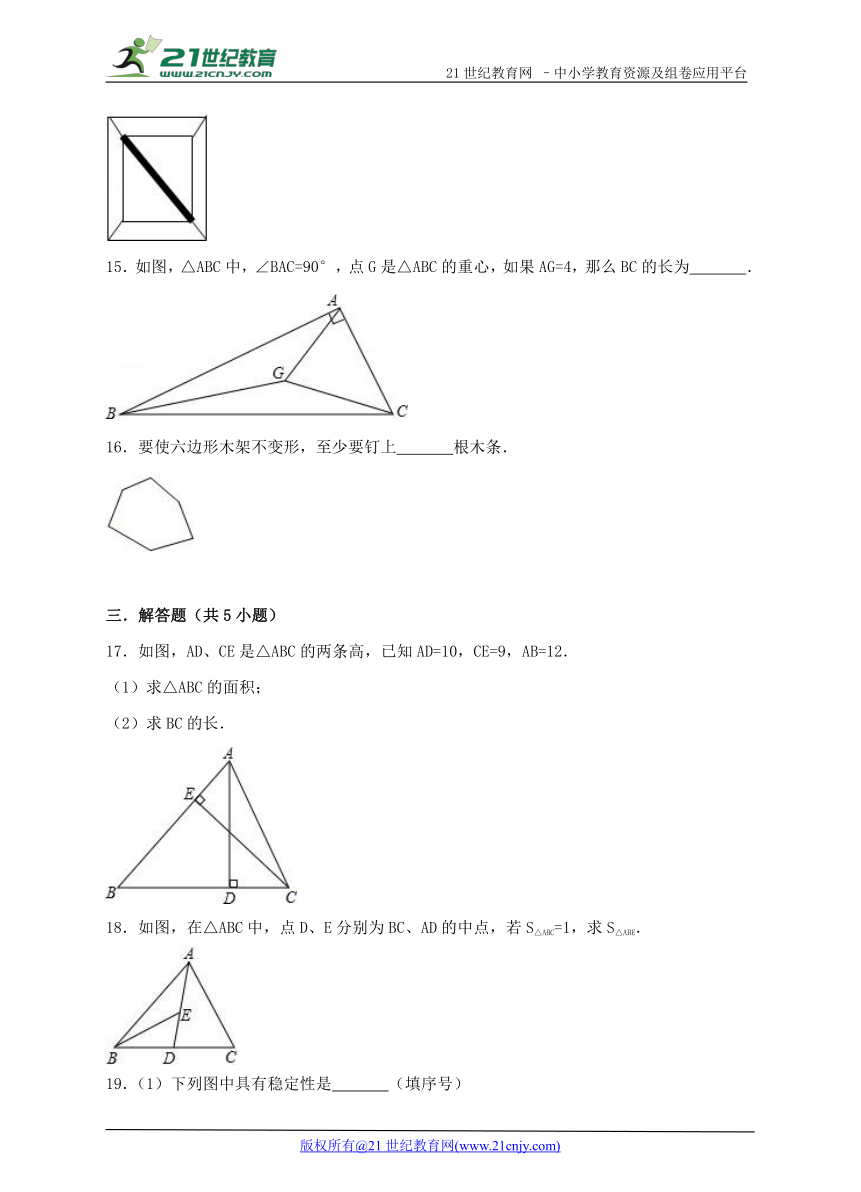
15.如图,△ABC中,∠BAC=90°,点G是△ABC的重心,如果AG=4,那么BC的长为 .
( http: / / www.21cnjy.com )
16.要使六边形木架不变形,至少要钉上 根木条.
( http: / / www.21cnjy.com )
三.解答题(共5小题)
17.如图,AD、CE是△ABC的两条高,已知AD=10,CE=9,AB=12.
(1)求△ABC的面积;
(2)求BC的长.
( http: / / www.21cnjy.com )
18.如图,在△ABC中,点D、E分别为BC、AD的中点,若S△ABC=1,求S△ABE.
( http: / / www.21cnjy.com )
19.(1)下列图中具有稳定性是 (填序号)
(2)对不具稳定性的图形,请适当地添加线段,使之具有稳定性.
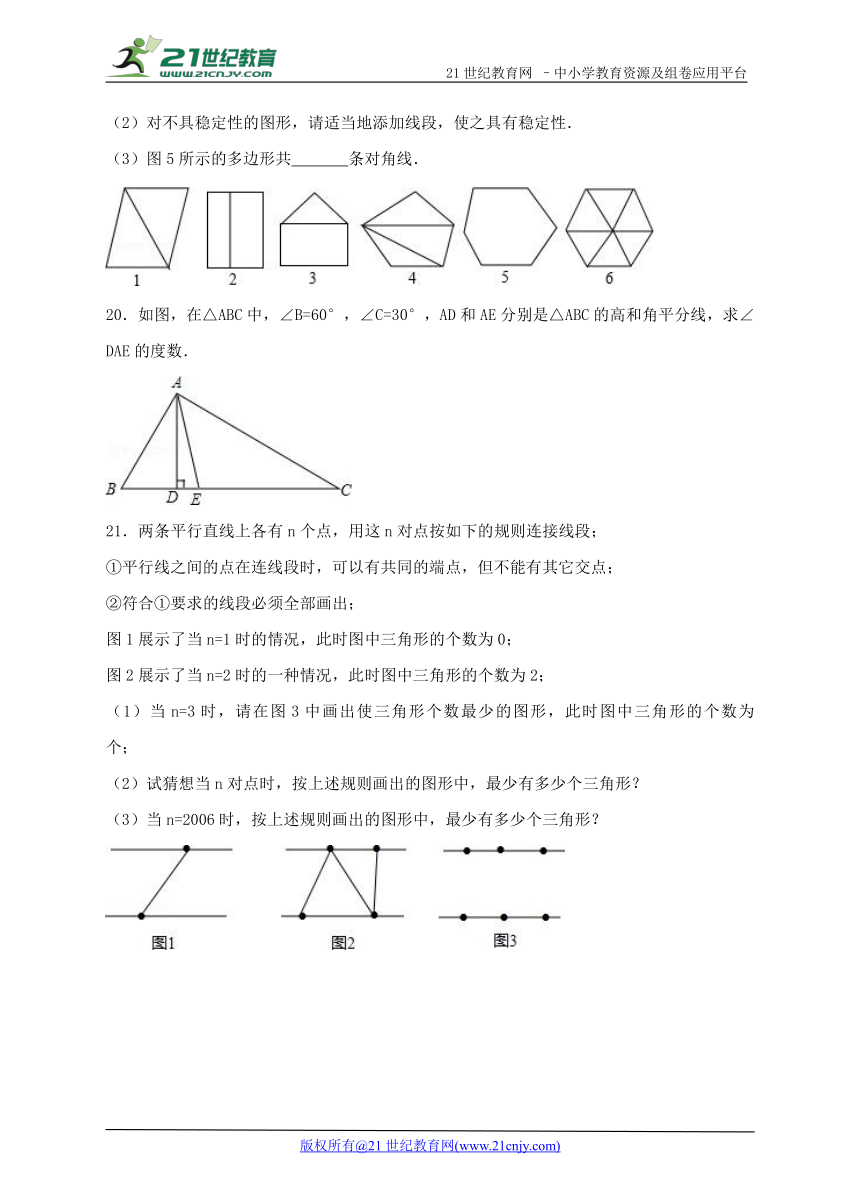
(3)图5所示的多边形共 条对角线.
( http: / / www.21cnjy.com )
20.如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.21·世纪*教育网
( http: / / www.21cnjy.com )
21.两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为 个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2006时,按上述规则画出的图形中,最少有多少个三角形?
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共9小题)
1.
【分析】根据三角形的分类情况可得答案.
解:三角形按角分类可以分为锐角三角形、直角三角形、钝角三角形,
故选:A.
2.
【分析】根据三角形的定义(由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形)找出图中的三角形.21教育网
解:根据图示知,图中以AB为边的三角形有:△ABD,△ABE,△ABC.共有3个;
故选:A.
3.
【分析】作哪一条边上的高,即从所对的顶点向这条边或这条边的延长线作垂线即可.
解:过点C作AB边的垂线,正确的是C.
故选:C.
4.
【分析】本题需要分类讨论:两边相等的三角形 ( http: / / www.21cnjy.com )称为等腰三角形,该等腰三角形可以是等腰直角三角形,该等腰三角形有可能是锐角三角形,也有可能是钝角三角形;
当有三边相等时,该三角形是等边三角形.等边三角形是一特殊的等腰三角形.
解:本题中三角形的分类是: ( http: / / www.21cnjy.com ).
故选:B.
5.
【分析】根据三角形的一个顶点到对边的垂线段叫做三角形的高对各选项分析判断后利用排除法求解.
解:A、△ABC中,AD是BC边上的高正确,故本选项错误;
B、△GBC中,CF是BG边上的高正确,故本选项错误;
C、△ABC中,GC是BC边上的高错误,故本选项正确;
D、△GBC中,GC是BC边上的高正确,故本选项错误.
故选:C.
6.
【分析】从三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高.
三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.2·1·c·n·j·y
三角形一边的中点与此边所对顶点的连线叫做三角形的中线.依此即可求解.
解:∵CD,CE,CF分别是△ABC的高、角平分线、中线,
∴CD⊥BE,∠ACE= ( http: / / www.21cnjy.com )∠ACB,AB=2BF,无法确定AE=BE.
故选:C.
7.
【分析】根据三角形的角的平分线、中线、高线的性质即可确定.
解:A、三角形的三条角平分线交于一点,是三角形的内心,故命题正确;
B、三角形的三条中线交于一点,是三角形的重心,故命题正确;
三角形的三条高所在的直线交于一点,三条高不一定相交,故C错误,D正确.
故选:C.
8.
【分析】根据三角形的三条中线都在三角形内部 ( http: / / www.21cnjy.com );三角形的三条角平分线都在三角形内部;三角形三条高可以在内部,也可以在外部,直角三角形有两条高在边上作答.
解:①、②正确;
而对于三角形三条高:
锐角三角形的三条高在三角形的内部;
直角三角形有两条高在边上;
钝角三角形有两条高在外部,故③错误.
故选:B.
9.
【分析】根据三角形的面积公式以及三角形的中线定义,知三角形的一边上的中线把三角形分成了等底同高的两个三角形,所以它们的面积相等.21cnjy.com
解:三角形一边上的中线把原三角形分成两个面积相等的三角形.
故选:B.
二.填空题(共7小题)
10.
【分析】利用三角中位线的性质得出DE ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )AB,进而求出即可.
解:∵在△ABC中,AD,BE是两条中线,
∴DE ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )AB,
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
故答案为:1:4.
11.
【分析】根据等底等高的两个 ( http: / / www.21cnjy.com )三角形面积相等知,三角形的中线把三角形的面积分为相等的两部分,所以△ADC的面积是△ABC的面积的一半,即9cm2.www.21-cn-jy.com
解:S△ADC=S△ABC÷2=18÷2=9cm2.
12.
【分析】根据三角形的面积公式即可求得.
解∵AD、BE分别是△ABC的高,
∴S△ABC= ( http: / / www.21cnjy.com )BC AD= ( http: / / www.21cnjy.com )AC BE,
∴BC AD=AC BE,
∵AD=4cm,BC=6cm,AC=5cm,
∴BE= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )cm,
故答案为 ( http: / / www.21cnjy.com )cm.
13.
【分析】根据三角形的中线把三角形分成面 ( http: / / www.21cnjy.com )积相等的两个三角形用S△ABC表示出△ABD、△ACD、△BDE,△CDE的面积,然后表示出△BCE的面积,再表示出△BEF的面积,即可得解.
解:如图,连接BE.
∵点D、E分别为BC、AD的中点,
∴S△ABD=S△ACD= ( http: / / www.21cnjy.com )S△ABC,
S△BDE= ( http: / / www.21cnjy.com )S△ABD= ( http: / / www.21cnjy.com )S△ABC,
S△CDE= ( http: / / www.21cnjy.com )S△ACD= ( http: / / www.21cnjy.com )S△ABC,
∴S△BCE=S△BDE+S△CDE= ( http: / / www.21cnjy.com )S△ABC+ ( http: / / www.21cnjy.com )S△ABC= ( http: / / www.21cnjy.com )S△ABC,
∵F是CE的中点,
∴S△BEF=S△BFC= ( http: / / www.21cnjy.com )S△BCE= ( http: / / www.21cnjy.com )× ( http: / / www.21cnjy.com )S△ABC= ( http: / / www.21cnjy.com )S△ABC,
∴S△BFC:S△ABC=1:4.
∵S△BFC=1,
∴S△ABC=4.
故答案为:4.
( http: / / www.21cnjy.com )
14.
【分析】在窗框上斜钉一根木条,构成三角形,故可用三角形的稳定性解释.
解:盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,这样就构成了三角形,故这样做的数学道理是三角形的稳定性.【来源:21·世纪·教育·网】
故应填:三角形的稳定性.
15.
【分析】延长AG交BC于点D,根据 ( http: / / www.21cnjy.com )重心的性质可知点D为BC的中点,且AG=2DG=4,则AD=6,再根据直角三角形斜边的中线等于斜边的一半即可求解.2-1-c-n-j-y
解:如图,延长AG交BC于点D.
∵点G是△ABC的重心,AG=4,
∴点D为BC的中点,且AG=2DG=4,
∴DG=2,
∴AD=AG+DG=6,
∵△ABC中,∠BAC=90°,AD是斜边的中线,
∴BC=2AD=12.
故答案为12.
( http: / / www.21cnjy.com )
16.
【分析】过同一顶点作对角线把木架分割成三角形,解答即可.
解:如图所示,至少要钉上3根木条.
故答案为:3.
( http: / / www.21cnjy.com )
三.解答题(共5小题)
17.
【分析】(1)根据三角形的面积等于底乘以高除以2列式计算即可得解;
(2)根据△ABC的面积列式计算即可得解.
解:(1)∵CE=9,AB=12,
∴△ABC的面积= ( http: / / www.21cnjy.com )×12×9=54;
(2)△ABC的面积= ( http: / / www.21cnjy.com )BC AD=54,
即 ( http: / / www.21cnjy.com )BC 10=54,
解得BC= ( http: / / www.21cnjy.com ).
18.
【分析】根据三角形的中线平分三角形面积进而得出答案.
解:∵点D、E分别是BC、AD边的中点,
∴S△ABD= ( http: / / www.21cnjy.com )S△ABC,S△ABE= ( http: / / www.21cnjy.com )S△ABD,
∴S△ABE= ( http: / / www.21cnjy.com )S△ABC,
∵S△ABC=1,
∴S△ABE=1× ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
19.
【分析】(1)根据三角形具有稳定性,只要图形分割成了三角形,则具有稳定性;
(2)将不具有稳定性的图形分割成三角形即可具有稳定性;
(3)n边形共有 ( http: / / www.21cnjy.com )条对角线,代入求解即可.
解:(1)具有稳定性的是①④⑥三个.
(2)如图所示:
( http: / / www.21cnjy.com )
(3)六边形的对角线有 ( http: / / www.21cnjy.com )=9条,
故答案为:①④⑥,9.
20.
【分析】先根据三角形的内角和定理得到∠BAC的度数,再利用角平分线的性质可求出∠BAE= ( http: / / www.21cnjy.com )∠BAC,而∠BAD=90°﹣∠B,然后利用∠DAE=∠BAE﹣∠BAD进行计算即可.
解:在△ABC中,∠B=60°,∠C=30°
∴∠BAC=180°﹣∠B﹣∠C=180°﹣30°﹣60°=90°
∵AD是的角平分线
∴∠BAE= ( http: / / www.21cnjy.com )∠BAC=45°,
∵AE是△ABC的高,
∴∠ADB=90°
∴在△ADB中,∠BAD=90°﹣∠B=90°﹣60°=30°
∴∠DAE=∠BAE﹣∠BAD=45°﹣30°=15°
21.
【分析】(1)根据题意,作图可得答 ( http: / / www.21cnjy.com )案;(2)分析可得,当n=1时的情况,此时图中三角形的个数为0,有0=2(1﹣1);当n=2时的一种情况,此时图中三角形的个数为2,有2=2(2﹣1);…故当有n对点时,最少可以画2(n﹣1)个三角形;(3)当n=2006时,按上述规则画出的图形中,最少有2×(2006﹣1)=4010个三角形.21世纪教育网版权所有
解:(1)
( http: / / www.21cnjy.com )
4个;
(2)当有n对点时,最少可以画2(n﹣1)个三角形;
(3)2×(2006﹣1)=4010个.
答:当n=2006时,最少可以画4010个三角形.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
9.1.1 认识三角形同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1. 由三条不在同一直线上的线段首尾顺次连结组成的平面图形叫三角形,这三条线段叫做三角形的边 . www-2-1-cnjy-com
2. 三角形中内角的一边与另一边的反向延长线所组成的角叫三角形的外角,在三角形的一个顶点处有两个外角,它们是一对对顶角 . 21*cnjy*com
3.三角形的分类
( http: / / www.21cnjy.com )
4. 三角形的三条中线、三条角平分线、三 ( http: / / www.21cnjy.com )条高(或所在的直线)都能交于一点 , 直角三角形三条高的交点就是直角顶点 ,钝角三角形有两条高位于三角形的外部.
基础知识和能力拓展精练
一.选择题(共9小题)
1.三角形按角分类可以分为( )
A.锐角三角形、直角三角形、钝角三角形
B.等腰三角形、等边三角形、不等边三角形
C.直角三角形、等边直角三角形
D.以上答案都不正确
2.如图,图中以AB为边的三角形的个数是( )
( http: / / www.21cnjy.com )
A.3 B.4 C.5 D.6
3.画△ABC中AB边上的高,下列画法中正确的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
4.至少有两边相等的三角形是( )
A.等边三角形 B.等腰三角形 C.等腰直角三角形 D.锐角三角形
5.如图,AD⊥BD于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )
( http: / / www.21cnjy.com )
A.△ABC中,AD是BC边上的高 B.△GBC中,CF是BG边上的高
C.△ABC中,GC是BC边上的高 D.△GBC中,GC是BC边上的高
6.如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
( http: / / www.21cnjy.com )
A.AB=2BF B.∠ACE= ( http: / / www.21cnjy.com )∠ACB C.AE=BE D.CD⊥BE
7.下面说法错误的是( )
A.三角形的三条角平分线交于一点
B.三角形的三条中线交于一点
C.三角形的三条高交于一点
D.三角形的三条高所在的直线交于一点
8.下列说法正确的是( )
①三角形的三条中线都在三角形内部;②三角形的三条角平分线都在三角形内部;③三角形三条高都在三角形的内部.【来源:21cnj*y.co*m】
A.①②③ B.①② C.②③ D.①③
9.三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
二.填空题(共7小题)
10.如图,在△ABC中,AD,BE是两条中线,则S△EDC:S△ABC= .
( http: / / www.21cnjy.com )
11.如图,AD是△ABC的中线,如果△ABC的面积是18cm2,则△ADC的面积是 cm2.
( http: / / www.21cnjy.com )
12.如图,AD,BE分别是△ABC的高,AD=4,BC=6,AC=5,则BE= .
( http: / / www.21cnjy.com )
13.如图,在△ABC中,点D、E、F分别为BC、AD、CE的中点.若S△BFC=1,则S△ABC= .
( http: / / www.21cnjy.com )
14.如图,盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,这样做的数学道理是 .21·cn·jy·com
( http: / / www.21cnjy.com )
15.如图,△ABC中,∠BAC=90°,点G是△ABC的重心,如果AG=4,那么BC的长为 .
( http: / / www.21cnjy.com )
16.要使六边形木架不变形,至少要钉上 根木条.
( http: / / www.21cnjy.com )
三.解答题(共5小题)
17.如图,AD、CE是△ABC的两条高,已知AD=10,CE=9,AB=12.
(1)求△ABC的面积;
(2)求BC的长.
( http: / / www.21cnjy.com )
18.如图,在△ABC中,点D、E分别为BC、AD的中点,若S△ABC=1,求S△ABE.
( http: / / www.21cnjy.com )
19.(1)下列图中具有稳定性是 (填序号)
(2)对不具稳定性的图形,请适当地添加线段,使之具有稳定性.
(3)图5所示的多边形共 条对角线.
( http: / / www.21cnjy.com )
20.如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.21·世纪*教育网
( http: / / www.21cnjy.com )
21.两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为 个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2006时,按上述规则画出的图形中,最少有多少个三角形?
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共9小题)
1.
【分析】根据三角形的分类情况可得答案.
解:三角形按角分类可以分为锐角三角形、直角三角形、钝角三角形,
故选:A.
2.
【分析】根据三角形的定义(由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形)找出图中的三角形.21教育网
解:根据图示知,图中以AB为边的三角形有:△ABD,△ABE,△ABC.共有3个;
故选:A.
3.
【分析】作哪一条边上的高,即从所对的顶点向这条边或这条边的延长线作垂线即可.
解:过点C作AB边的垂线,正确的是C.
故选:C.
4.
【分析】本题需要分类讨论:两边相等的三角形 ( http: / / www.21cnjy.com )称为等腰三角形,该等腰三角形可以是等腰直角三角形,该等腰三角形有可能是锐角三角形,也有可能是钝角三角形;
当有三边相等时,该三角形是等边三角形.等边三角形是一特殊的等腰三角形.
解:本题中三角形的分类是: ( http: / / www.21cnjy.com ).
故选:B.
5.
【分析】根据三角形的一个顶点到对边的垂线段叫做三角形的高对各选项分析判断后利用排除法求解.
解:A、△ABC中,AD是BC边上的高正确,故本选项错误;
B、△GBC中,CF是BG边上的高正确,故本选项错误;
C、△ABC中,GC是BC边上的高错误,故本选项正确;
D、△GBC中,GC是BC边上的高正确,故本选项错误.
故选:C.
6.
【分析】从三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高.
三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.2·1·c·n·j·y
三角形一边的中点与此边所对顶点的连线叫做三角形的中线.依此即可求解.
解:∵CD,CE,CF分别是△ABC的高、角平分线、中线,
∴CD⊥BE,∠ACE= ( http: / / www.21cnjy.com )∠ACB,AB=2BF,无法确定AE=BE.
故选:C.
7.
【分析】根据三角形的角的平分线、中线、高线的性质即可确定.
解:A、三角形的三条角平分线交于一点,是三角形的内心,故命题正确;
B、三角形的三条中线交于一点,是三角形的重心,故命题正确;
三角形的三条高所在的直线交于一点,三条高不一定相交,故C错误,D正确.
故选:C.
8.
【分析】根据三角形的三条中线都在三角形内部 ( http: / / www.21cnjy.com );三角形的三条角平分线都在三角形内部;三角形三条高可以在内部,也可以在外部,直角三角形有两条高在边上作答.
解:①、②正确;
而对于三角形三条高:
锐角三角形的三条高在三角形的内部;
直角三角形有两条高在边上;
钝角三角形有两条高在外部,故③错误.
故选:B.
9.
【分析】根据三角形的面积公式以及三角形的中线定义,知三角形的一边上的中线把三角形分成了等底同高的两个三角形,所以它们的面积相等.21cnjy.com
解:三角形一边上的中线把原三角形分成两个面积相等的三角形.
故选:B.
二.填空题(共7小题)
10.
【分析】利用三角中位线的性质得出DE ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )AB,进而求出即可.
解:∵在△ABC中,AD,BE是两条中线,
∴DE ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )AB,
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
故答案为:1:4.
11.
【分析】根据等底等高的两个 ( http: / / www.21cnjy.com )三角形面积相等知,三角形的中线把三角形的面积分为相等的两部分,所以△ADC的面积是△ABC的面积的一半,即9cm2.www.21-cn-jy.com
解:S△ADC=S△ABC÷2=18÷2=9cm2.
12.
【分析】根据三角形的面积公式即可求得.
解∵AD、BE分别是△ABC的高,
∴S△ABC= ( http: / / www.21cnjy.com )BC AD= ( http: / / www.21cnjy.com )AC BE,
∴BC AD=AC BE,
∵AD=4cm,BC=6cm,AC=5cm,
∴BE= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )cm,
故答案为 ( http: / / www.21cnjy.com )cm.
13.
【分析】根据三角形的中线把三角形分成面 ( http: / / www.21cnjy.com )积相等的两个三角形用S△ABC表示出△ABD、△ACD、△BDE,△CDE的面积,然后表示出△BCE的面积,再表示出△BEF的面积,即可得解.
解:如图,连接BE.
∵点D、E分别为BC、AD的中点,
∴S△ABD=S△ACD= ( http: / / www.21cnjy.com )S△ABC,
S△BDE= ( http: / / www.21cnjy.com )S△ABD= ( http: / / www.21cnjy.com )S△ABC,
S△CDE= ( http: / / www.21cnjy.com )S△ACD= ( http: / / www.21cnjy.com )S△ABC,
∴S△BCE=S△BDE+S△CDE= ( http: / / www.21cnjy.com )S△ABC+ ( http: / / www.21cnjy.com )S△ABC= ( http: / / www.21cnjy.com )S△ABC,
∵F是CE的中点,
∴S△BEF=S△BFC= ( http: / / www.21cnjy.com )S△BCE= ( http: / / www.21cnjy.com )× ( http: / / www.21cnjy.com )S△ABC= ( http: / / www.21cnjy.com )S△ABC,
∴S△BFC:S△ABC=1:4.
∵S△BFC=1,
∴S△ABC=4.
故答案为:4.
( http: / / www.21cnjy.com )
14.
【分析】在窗框上斜钉一根木条,构成三角形,故可用三角形的稳定性解释.
解:盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,这样就构成了三角形,故这样做的数学道理是三角形的稳定性.【来源:21·世纪·教育·网】
故应填:三角形的稳定性.
15.
【分析】延长AG交BC于点D,根据 ( http: / / www.21cnjy.com )重心的性质可知点D为BC的中点,且AG=2DG=4,则AD=6,再根据直角三角形斜边的中线等于斜边的一半即可求解.2-1-c-n-j-y
解:如图,延长AG交BC于点D.
∵点G是△ABC的重心,AG=4,
∴点D为BC的中点,且AG=2DG=4,
∴DG=2,
∴AD=AG+DG=6,
∵△ABC中,∠BAC=90°,AD是斜边的中线,
∴BC=2AD=12.
故答案为12.
( http: / / www.21cnjy.com )
16.
【分析】过同一顶点作对角线把木架分割成三角形,解答即可.
解:如图所示,至少要钉上3根木条.
故答案为:3.
( http: / / www.21cnjy.com )
三.解答题(共5小题)
17.
【分析】(1)根据三角形的面积等于底乘以高除以2列式计算即可得解;
(2)根据△ABC的面积列式计算即可得解.
解:(1)∵CE=9,AB=12,
∴△ABC的面积= ( http: / / www.21cnjy.com )×12×9=54;
(2)△ABC的面积= ( http: / / www.21cnjy.com )BC AD=54,
即 ( http: / / www.21cnjy.com )BC 10=54,
解得BC= ( http: / / www.21cnjy.com ).
18.
【分析】根据三角形的中线平分三角形面积进而得出答案.
解:∵点D、E分别是BC、AD边的中点,
∴S△ABD= ( http: / / www.21cnjy.com )S△ABC,S△ABE= ( http: / / www.21cnjy.com )S△ABD,
∴S△ABE= ( http: / / www.21cnjy.com )S△ABC,
∵S△ABC=1,
∴S△ABE=1× ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
19.
【分析】(1)根据三角形具有稳定性,只要图形分割成了三角形,则具有稳定性;
(2)将不具有稳定性的图形分割成三角形即可具有稳定性;
(3)n边形共有 ( http: / / www.21cnjy.com )条对角线,代入求解即可.
解:(1)具有稳定性的是①④⑥三个.
(2)如图所示:
( http: / / www.21cnjy.com )
(3)六边形的对角线有 ( http: / / www.21cnjy.com )=9条,
故答案为:①④⑥,9.
20.
【分析】先根据三角形的内角和定理得到∠BAC的度数,再利用角平分线的性质可求出∠BAE= ( http: / / www.21cnjy.com )∠BAC,而∠BAD=90°﹣∠B,然后利用∠DAE=∠BAE﹣∠BAD进行计算即可.
解:在△ABC中,∠B=60°,∠C=30°
∴∠BAC=180°﹣∠B﹣∠C=180°﹣30°﹣60°=90°
∵AD是的角平分线
∴∠BAE= ( http: / / www.21cnjy.com )∠BAC=45°,
∵AE是△ABC的高,
∴∠ADB=90°
∴在△ADB中,∠BAD=90°﹣∠B=90°﹣60°=30°
∴∠DAE=∠BAE﹣∠BAD=45°﹣30°=15°
21.
【分析】(1)根据题意,作图可得答 ( http: / / www.21cnjy.com )案;(2)分析可得,当n=1时的情况,此时图中三角形的个数为0,有0=2(1﹣1);当n=2时的一种情况,此时图中三角形的个数为2,有2=2(2﹣1);…故当有n对点时,最少可以画2(n﹣1)个三角形;(3)当n=2006时,按上述规则画出的图形中,最少有2×(2006﹣1)=4010个三角形.21世纪教育网版权所有
解:(1)
( http: / / www.21cnjy.com )
4个;
(2)当有n对点时,最少可以画2(n﹣1)个三角形;
(3)2×(2006﹣1)=4010个.
答:当n=2006时,最少可以画4010个三角形.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
