2018年高考数学三轮冲刺之专题突破详解:专题18 演绎推理与合情推理(含解析)
文档属性
| 名称 | 2018年高考数学三轮冲刺之专题突破详解:专题18 演绎推理与合情推理(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-23 00:00:00 | ||
图片预览




文档简介
一.高考命题知识点和类型
1.归纳法
2.类比法
3.数学归纳法
4.分析法
5.综合法
6.反证法
7.三段论
【知识要点】
1.合情推理
归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,统称为合情推理.
当前提为真时,结论可能为真的推理叫合情推理.数学中常见的合情推理有:归纳和类比推理.
(1)根据某类事物的部分对象具有的某些特征推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理,称为归纳推理(简称归纳).简言之,归纳推理是由部分到整体、由个别到一般的推理.
(2)由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理 (简称类比).简言之,类比推理是由特殊到特殊的推理.
2.演绎推理
(1)定义:演绎推理是根据已有的事实和正确的结论(包括定义、公理、定理等),按照严格的逻辑法则得到新结论的推理过程,简言之,演绎推理是由一般到特殊的推理.
(2)演绎推理的一般模式——“三段论”
①大前提——已知的一般性的原理;
②小前提——所研究的特殊情况;
③结论——根据一般原理,对特殊情况做出的判断.
1.合情推理主要包括归纳推理和类比推理
在数学研究中,在得到一个新结论前,合情推理能帮助猜测和发现结论.证明一个数学结论之前,合情推理常常能为证明提供思路与方向.
2.合情推理的过程
→→→
3.演绎推理
演绎推理是从一般性的原理出发,推出某个特殊情况的结论的推理方法.是由一般到特殊的推理,常用的一般模式是三段论.数学问题的证明主要通过演绎推理来进行.
4.注意归纳和类比的结论的可靠性有待于证明.
1.直接证明
(1)从原命题的条件逐步推得命题成立的证明称为直接证明.综合法和分析法是直接证明中最基本的两种证明方法,也是解决数学问题时常用的思维方法.
(2)从已知条件出发,以已知的定义、公理、定理为依据,逐步下推,直到推出要证明的结论为止.这种证明方法常称为综合法.
推证过程如下:
→→→…→
(3)从要证明的结论出发,追溯导致结论成立的充分条件,逐步上溯,直到使结论成立的条件和已知条件或已知事实吻合为止.这种证明方法常称为分析法.
推论过程如下:
→→→…→得到一个明显成立的条件.
P—表示条件,Q—表示要证的结论.
2.间接证明——反证法
(1)假设原命题不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立,这样的证明方法叫做反证法.
(2)反证法的特点:先假设原命题不成立,再在正确的推理下得出矛盾,所得矛盾可以是与已知条件矛盾,或与假设矛盾,或与定义、公理、定理、事实矛盾等.
推论过程如下:
→→→…→得到一个明显成立的条件.
P—表示条件,Q—表示要证的结论.
2.间接证明——反证法
(1)假设原命题不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立,这样的证明方法叫做_________.
(2)反证法的特点:先假设原命题__________成立,再在正确的推理下得出矛盾,所得矛盾可以是与已知条件矛盾,或与假设矛盾,或与定义、公理、定理、事实矛盾等.
2.关于反证法
使用反证法证明的关键是在正确的推理下得出矛盾,这个矛盾可以是与已知条件矛盾,或与假设矛盾,或与定义、公理、定理、公式、事实矛盾等.
反证法的步骤:(1)反设;(2)推出矛盾;(3)下结论.
矛盾的主要类型:(1)与假设矛盾;(2)与数学公式、法则、公理、定理、定义或已被证明了的结论矛盾;(3)与公认的简单事实矛盾;(4)自相矛盾.
1.数学归纳法是专门证明与正整数集有关的命题的一种方法.它是一种完全归纳法,是对不完全归纳法的完善.
2.证明代数恒等式的关键是第二步,将式子转化成与归纳假设的结构相同的形式——凑假设,然后利用归纳假设,经过恒等变形,得到结论所需要的形式——凑结论.
3.用数学归纳法证明不等式的关键是第二步,利用证明不等式的方法(如放缩)把式子化为n=k+1成立时的式子.
4.用数学归纳法证明几何问题时,要注意结合几何图形的性质,在求由“n=k到n=k+1”增加的元素个数时,可以先用不完全归纳法找其变化规律.
5.由有限个特殊事例进行归纳、猜想,而得出一般性结论,然后加以证明是科学研究的重要思想方法,研究与正整数有关的数学问题,此方法尤为重要,如猜想数列的通项an或前n项和Sn,解决与自然数有关的探索性、开放性问题等.这里猜想必须准确,证明必须正确.既用到合情推理,又用到演绎推理.猜想的准确与否可用证明来检验,否则不妨再分析,再猜想,再证明,猜想是证明的前提,证明可论证猜想的可靠性,二者相辅相成.
二.命题类型演练和命题陷阱
1.归纳法
例1已知数列满足, ,则( )
A. B. C. D.
【答案】A
【解析】数列满足, , ,
,由此猜想,故选A.
练习1.将正整数排成下表:
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
……………
则在表中数字2017出现在( )
A. 第44行第80列 B. 第45行第80列 C. 第44行第81列 D. 第45行第81列
【答案】D
【解析】因为每行的最后一个数分别为1,4,9,16,…,所以由此归纳出第n行的最后一个数为n2.
因为442=1936,452=2025,
所以2017出现在第45行上.
又由2017﹣1936=81,
故2017出现在第81列,
故选:D
练习2. 《聊斋志异》中有这样一首诗:“挑水砍柴不堪苦,请归但求穿墙术. 得诀自诩无所阻,额上坟起终不悟.”在这里,我们称形如以下形式的等式具有“穿墙术”: , ,则按照以上规律,若具有 “穿墙术”,则n=
A. 35 B. 48 C. 63 D. 80
【答案】C
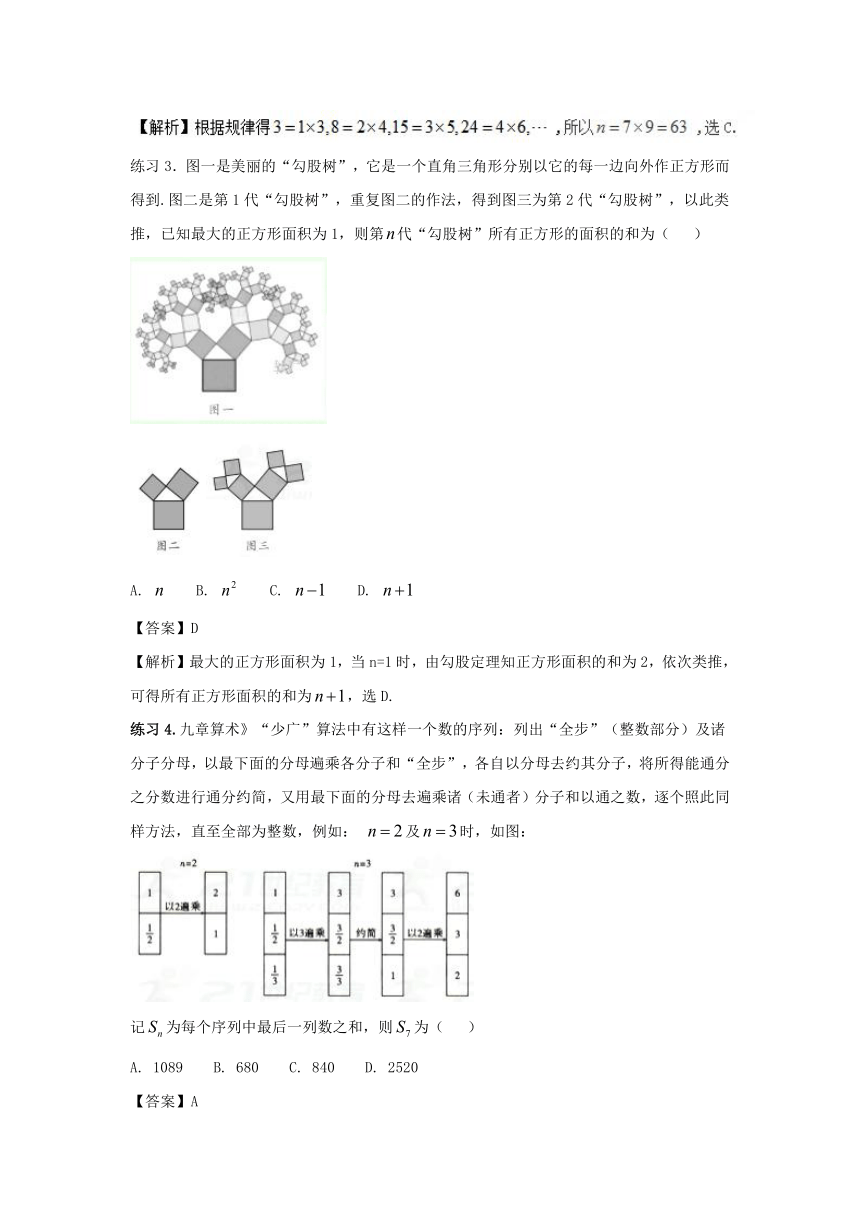
练习3.图一是美丽的“勾股树”,它是一个直角三角形分别以它的每一边向外作正方形而得到.图二是第1代“勾股树”,重复图二的作法,得到图三为第2代“勾股树”,以此类推,已知最大的正方形面积为1,则第代“勾股树”所有正方形的面积的和为( )
A. B. C. D.
【答案】D
【解析】最大的正方形面积为1,当n=1时,由勾股定理知正方形面积的和为2,依次类推,可得所有正方形面积的和为,选D.
练习4.九章算术》“少广”算法中有这样一个数的序列:列出“全步”(整数部分)及诸分子分母,以最下面的分母遍乘各分子和“全步”,各自以分母去约其分子,将所得能通分之分数进行通分约简,又用最下面的分母去遍乘诸(未通者)分子和以通之数,逐个照此同样方法,直至全部为整数,例如: 及时,如图:
记为每个序列中最后一列数之和,则为( )
A. 1089 B. 680 C. 840 D. 2520
【答案】A
【解析】当时,序列如图:
故练习5. 如图所示为计算机科学中的蛇形模型,则第20行从左到右第4个数字为__________.
【答案】194
练习6.观察下列等式:1=++;1=+++;1=++++;…,以此类推,1=++++++,其中n∈N*.则n=________.
【答案】12
【解析】1=+(-)+,1=+(-)+(-)+,
1=+(-)+(-)+(-)+,…,以此类推,
故1=+(-)+(-)+(-)+(-)+(-)+
=++++++,故n=12.
故答案为:12
【规律方法总结】:归纳推理的一般步骤: 一、通过观察个别情况发现某些相同的性质. 二、从已知的相同性质中推出一个明确表述的一般性命题(猜想). 常见的归纳推理分为数的归纳和形的归纳两类:(1) 数的归纳包括数的归纳和式子的归纳,解决此类问题时,需要细心观察,寻求相邻项及项与序号之间的关系,同时还要联系相关的知识,如等差数列、等比数列等;(2) 形的归纳主要包括图形数目的归纳和图形变化规律的归纳.
练习7. 某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.
(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
【答案】(1)(2)见解析
【解析】(1).
(2)三角恒等式:.
证明如下:左边
2.类比法
例2. 二维空间中,圆的一维测度(周长),二维测度(面积),三维空间中,球的二维测度(表面积),三维测度(体积),应用合情推理,若四维空间中,“超球”的三维测度,则其思维测度W=( )
A. B. C. D.
【答案】A
练习1. 如图所示,由曲线y=x2,直线x=a,x=a+1(a>0)及x轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即.运用类比推理,若对?n∈N*, 恒成立,则实数A=________.
【答案】
【解析】令,
依据类比推理可得A1=dx=ln(n+1)-lnn,A2=dx=ln(n+2)-ln(n+1),…,An=dx=ln(2n)-ln(2n-1),所以A=A1+A2+…+An=ln(n+1)-lnn+ln(n+2)-ln(n+1)+…+ln(2n)-ln(2n-1)=ln(2n)-lnn=ln 2.
练习2. 我国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一直角边为股,斜边为弦.若a,b,c为直角三角形的三边,其中c为斜边,则a2+b2=c2,称这个定理为勾股定理.现将这一定理推广到立体几何中:在四面体O-ABC中,∠AOB=∠BOC=∠COA=90°,S为顶点O所对面的面积,S1,S2,S3分别为侧面△OAB,△OAC,△OBC的面积,则下列选项中对于S,S1,S2,S3满足的关系描述正确的为( )
A. S2=S+S+S B.
C. S=S1+S2+S3 D.
【答案】A
【解析】如图,作OD⊥BC于点D,连接AD,由立体几何知识知,AD⊥BC,从而S2=(BC·AD)2=BC2·AD2=BC2·(OA2+OD2)= (OB2+OC2)·OA2+BC2·OD2=(OB·OA)2+(OC·OA)2+(BC·OD)2=.
练习3. 对于问题“已知关于x的不等式ax2+bx+c>0的解集为(-1,2),解关于x的不等式ax2-bx+c>0”,给出如下一种解法:
由ax2+bx+c>0的解集为(-1,2),得a(-x)2+b(-x)+c>0的解集为(-2,1),即关于x的不等式ax2-bx+c>0的解集为(-2,1).
思考上述解法,若关于x的不等式的解集为,则关于x的不等式的解集为( )
A. (-3,-1)∪(1,2) B. (1,2)
C. (-1,2) D. (-3,2)
【答案】A
【解析】由关于x的不等式的解集为,得的解集为(-3,-1)∪(1,2),即关于x的不等式的解集为(-3,-1)∪(1,2).
练习3. .已知数列{an}为等差数列,若am=a,an=b(n-m≥1,m,n∈N*),则.类比上述结论,对于等比数列{bn}(bn>0,n∈N*),若bm=c,bn=d(n-m≥2,m,n∈N*),则可以得到bm+n等于( )
A. B.
C. D.
【答案】C
【解析】观察{an}的性质: ,则联想nb-ma对应等比数列{bn}中的,
而{an}中除以(n-m)对应等比数列中开(n-m)次方,故bm+n=.
练习4. 中国有个名句“运筹帷幄之中,决胜千里之外”.其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算.算筹的摆放形式有纵横两种形式.如图,表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推,例如用算筹表示就是,则用算筹表示为( )
A. B.
C. D.
【答案】B
故答案为:B。
练习5. 的三边长分别为, 的面积为,内切圆半径为,则;类比这个结论可知: 四面体的四个面的面积分别为,内切球的半径为,四面体的体积为, ( )
A. B.
C. D.
【答案】C
【解析】
3.数学归纳法
例3. 1.下面四个判断中,正确的是( )
A. 式子,当时为1
B. 式子 ,当时为
C. 式子,当时为
D. 设,则
【答案】C
【解析】对于A,当n=1时,f(k)恒为1+k,错误;
对于B,当n=1时,f(k)恒为1,错误;
对于C,当n=1时,f(n)为,正确;
对于D,f(k+1)=f(k)+﹣,错误;
故选:C.
练习1. 用数学归纳法证明时,从“
到”左边需增乘的代数式为( )
A. B. C. D.
【答案】D
练习2. 如图所示,将若干个点摆成三角形图案,每条边(包括两个端点)有n(n>1,n∈N)个点,相应的图案中总的点数记为an,则等于( )
A. B.
C. D.
【答案】C
【解析】每条边有n个点,所以3条边有3n个点,三角形的3个顶点重复计算了一次,所以减3个顶点,即an=3n-3,那么,
即 ,故选C.
4.分析法
例4. 淮北一中艺术节对摄影类的A,B,C,D四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是C或D作品获得一等奖”;
乙说:“B作品获得一等奖”;
丙说:“A,D两项作品未获得一等奖”;
丁说:“是C作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是( ).
A. A作品 B. B作品 C. C作品 D. D作品
【答案】B
故选:B.
练习1. 某班有三个小组,甲、乙、丙三人分属不同的小组.某次数学考试成绩公布情况如下:甲和三人中的第3小组那位不一样,丙比三人中第1小组的那位的成绩低,三人中第3小组的那位比乙分数高。若甲、乙、丙三人按数学成绩由高到低排列,正确的是( )
A. 甲、乙、丙 B. 甲、丙、乙 C. 乙、甲、丙 D. 丙、甲、乙
【答案】B
【解析】甲和三人中的第小组那位不一样,说明甲不在第小组;三人中第小组那位比乙分数高,说明乙不在第3组,说明丙在第3组,又第3组成绩低于第1组,大于乙,这时可得乙为第2组,甲为第1组,那么成绩从高到低为:甲、丙、乙,故选B.
练习2.老师在四个不同的盒子里面放了4张不同的扑克牌,分别是红桃,梅花,方片以及黑桃,让明、小红、小张、小李四个人进行猜测:
小明说:第1个盒子里面放的是梅花,第3个盒子里面放的是方片;
小红说:第2个盒子里面饭的是梅花,第3个盒子里放的是黑桃;
小张说:第4个盒子里面放的是黑桃,第2个盒子里面放的是方片;
小李说:第4个盒子里面放的是红桃,第3个盒子里面放的是方片;
老师说:“小明、小红、小张、小李,你们都只说对了一半.”则可以推测,第4个盒子里装的是( )
A. 红桃或黑桃 B. 红桃或梅花
C. 黑桃或方片 D. 黑桃或梅花
【答案】A
【解析】因为四个人都只猜对了一半,故有一下两种可能:
(1)当小明猜对第1个盒子里面放的是梅花A时,第3个盒子里面放的不是方片A,则小李猜对第4个盒子里面放的时红桃A,小张猜对第2个盒子里面放的是方片A,小红猜对第3个盒子里面放的是黑桃A;
(2)若小明猜对的是第3个盒子里面放的是方片A,则第1个盒子里面放的不是梅花A,小红猜对第2个盒子里面放的是梅花A,小张猜对第4个盒子里面放的是黑桃A,小李猜对第3个盒子里面放的是方片A,则第一个盒子只能是红桃A,
故选A.
5.综合法
例5. 德国大数学家高斯年少成名,被誉为数学王子.19岁的高斯得到了一个数学史上非常重要的结论,就是《正十七边形尺规作图之理论与方法》, 在其年幼时,对1+2+3+…+100的求和运算中,提出了倒序相加法的原理,该原理基于所给数据前后对应项的和呈现一定的规律生成,因此,此方法也被称为高斯算法.现有函数f(x)=,则f(1)+f(2)+…+f(m+2017)等于( )
A. B. C. D.
【答案】C
【解析】f(1)+f(2)+f(3)+…+f(m+2017)=++…++,
又f(1)+f(2)+f(3)+…+f(m+2017)=++…++,
两式相加可得f(1)+f(2)+f(3)+…+f(m+2017)=.
故选:C
练习1. 若a,b是常数,a>0,b>0,a≠b,x,y∈(0,+∞),则,当且仅当=时取等号.利用以上结论,可以得到函数f(x)= (0A. 5 B. 15
C. 25 D. 2
【答案】C
【解析】由题意可得f(x)==≥=25,
当且仅当=,即x=时取等号,故最小值为25.
故选:C
练习1. 在直角坐标平面上的一列点简记为若由构成的数列满足其中为方向与轴正方向相同的单位向量,则称为点列.有下列说法
①为点列;
②若为点列,且点在点的右上方.任取其中连续三点则可以为锐角三角形;
③若为点列,正整数若,满足则
④若为点列,正整数若,满足则.
其中,正确说法的个数为()
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】①由题意可知, ,显然有是点列,①正确;②在中, , , 点在点的右上方, 为点列, , ,则, 为钝角, 为钝角三角形, 不可以为锐角三角形,②错;
③, ,
,③正确;
④同理②, 由于为点列,于是,可推导, ,即,④正确,正确说法的个数为,故选C.
6.反证法
例6.(1)用分析法证明:当, 时, ;
(2)证明:对任意, , , 这个值至少有一个不小于.
【答案】(1)见解析;(2)见解析
(2)假设这3个值没有一个不小于0,
即
则,(*)
而.
这与(*)矛盾,所以假设不成立,即原命题成立.
【点睛】
分析法是“执果索因”,是寻找命题成立的充分条件,如果条件成立的话,则命题成立。
反证法是,假设命题的结论不成立,即反面成立,再根据假设及条件及己知公式定理,推出与条件或定理公理或已知事实矛盾的结论,即假设不成立,原命题成立。
练习1.已知,则下列三个数 ( )
A. 都大于6 B. 至少有一个不大于6
C. 都小于6 D. 至少有一个不小于6
【答案】D
【解析】设都小于6,
则++<18,
利用基本不等式可得+ ≥2+2+2=4+8+6=18,
这与假设所得结论矛盾,故假设不成立,
故下列三个数至少有一个不小于6,
故选:D
2.已知,则下列三个数 ( )
A. 都大于6 B. 至少有一个不大于6
C. 都小于6 D. 至少有一个不小于6
【答案】D
【解析】设都大于6,
则++<18,
利用基本不等式可得+ ≥2+2+2=4+8+6=18,
这与假设所得结论矛盾,故假设不成立,
故下列三个数至少有一个不小于6,
故选:D
3.① 已知,求证,用反证法证明时,可假设;② 设为实数, ,求证与中至少有一个不小于,有反证法证明时可假设,且,以下说法正确的是( )
A. ①与②的假设都错误 B. ①与②的假设都正确
C. ①的假设正确,②的假设错误 D. ①的假设错误,②的假设正确
【答案】C
【解析】①用反证法证明时,假设命题为假,应为全面否定,所以的假命题应为,故①的假设正确;②与中至少有一个不小于的否定为与中都小于,故②的假设错误;故选C.
4.设、、都是正数,则、、三个数( )
A. 都大于 B. 都小于 C. 至少有一个大于 D. 至少有一个不小于
【答案】D
【解析】假设、、三个数都小于,则:
,
利用均值不等式的结论有:
得到矛盾的结论,可见假设不成立,
即、、三个数中至少有一个不小于.
本题选择D选项.
【方法总结】:用反证法证明不等式要把握三点:(1)必须先否定结论,即肯定结论的反面;(2)必须从否定结论进行推理,即应把结论的反面作为条件,且必须依据这一条件进行推证;(3)推导出的矛盾可能多种多样,有的与已知矛盾,有的与假设矛盾,有的与已知事实矛盾等,且推导出的矛盾必须是明显的.
5.用反证法证明命题:“,若可被整除,那么中至少有一个能被整除.”时,假设的内容应该是
A. 都能被5整除 B. 都不能被5整除
C. 不都能被5整除 D. 能被5整除
【答案】B
6.⑴当时,求证: ;
⑵已知, .试证明至少有一个不小于.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:
⑴由,
当时,可得,即可证明结论;
⑵可用反证法:假设都小于,即,可得,
进而,即可得到矛盾,即可作出证明.
试题解析:
⑴
∵ ∴
∴
⑵假设都小于,即
则有 ①
而 ②
①与②矛盾
故至少有一个不小于.
7.已知是数列的前项和,并且,对任意正整数, ,设().
(1)证明:数列是等比数列,并求的通项公式;
(2)设,求证:数列不可能为等比数列.
【答案】(1)答案见解析;(2)证明见解析.
∴bn=an+1-2an,
∴bn+1=an+2-2an+1=4(an+1-an)-2an+1,bn+1=2(an+1-2an)=2bn(n∈N*),
∴,∴{bn}是以2为公比的等比数列,
∵b1=a2-2a1,而a1+a2=4a1+2,∴a2=3a1+2=5,b1=5-2=3,
∴bn=3?2n-1(n∈N*)
(II),假设为等比数列,则有
, n≥2, 则有=0
与 ≥1矛盾,所以假设不成立,则原结论成立,即
数列不可能为等比数列
8.(1)若都是正实数,且,求证: 与中至少有一个成立。
(2)求证:
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)本题证明结论中结构较复杂,而其否定结构简单,故可用反证法证明其否定不成立,以此来证明结论成立.(2)采用分析法从要证的结果入手去证明不等式即可。
解析:
(1)假设<2和<2都不成立,即≥2和≥2同时成立. ∵x>0且y>0,∴1+x≥2y,且1+y≥2x.
两式相加得2+x+y≥2x+2y,∴x+y≤2.这与已知条件x+y>2矛盾,
∴<2和<2中至少有一个成立.
(2)原式子等价于2,两边平方得到 ,得证。
9.证明: 不是有理数.
【解析】试题分析:利用反证法假设是有理数,进而利用有理数的性质分析得出矛盾,进而得出答案.
试题解析:
假设为有理数
那么存在两个互质的正整数,使得: ,
于是,两边平方得
由是偶数,可得是偶数.
而只有偶数的平方才是偶数,所以也是偶数.
因此可设, 是正整数,代入上式,得: ,即.
所以也是偶数,这样都是偶数,不互质,这与假设互质矛盾.
因此不是有理数.
7.三段论
例7. 有一段“三段论”推理是这样的:
对于可导函数f(x),如果f′(x0)=0,那么x=x0是函数f(x)的极值点,因为函数f(x)=x3在x=0处的导数值f′(0)=0,所以x=0是函数f(x)=x3的极值点.以上推理中( )
A. 小前提错误 B. 大前提错误
C. 推理形式错误 D. 结论正确
【答案】B
【解析】大前提:如果f′(x0)=0,那么x=x0是函数f(x)的极值点,错误.
练习1. 推理过程:“因为无理数是无限小数, 是无限小数,所以是无理数”,以下说法正确的是( )
A. 完全归纳推理,结论正确 B. 三段论推理,结论正确
C. 传递性关系推理,结论正确 D. 大前提正确,推出的结论错误
【答案】D
故选:D.
三.高考真题演练
1. 【2017课标II,理7】甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩。老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩。看后甲对大家说:我还是不知道我的成绩。根据以上信息,则( )
A.乙可以知道四人的成绩 B.丁可以知道四人的成绩
C.乙、丁可以知道对方的成绩 D.乙、丁可以知道自己的成绩
【答案】D
【解析】
故选D。
【考点】合情推理
【名师点睛】合情推理主要包括归纳推理和类比推理。数学研究中,在得到一个新结论前,合情推理能帮助猜测和发现结论,在证明一个数学结论之前,合情推理常常能为证明提供思路与方向。合情推理仅是“合乎情理”的推理,它得到的结论不一定正确。而演绎推理得到的结论一定正确(前提和推理形式都正确的前提下)。
2.【2015高考广东,理8】若空间中个不同的点两两距离都相等,则正整数的取值( )
A.大于5 B. 等于5 C. 至多等于4 D. 至多等于3
【答案】.
【解析】显然正三角形和正四面体的顶点是两两距离相等的,即或时命题成立,由此可排除、、,故选.
【考点定位】空间想象能力,推理能力,含有量词命题真假的判断.
【名师点睛】本题主要考查学生的空间想象能力,推理求解能力和含有量词命题真假的判断,此题属于中高档题,如果直接正面解答比较困难,考虑到是选择题及选项信息可以根据平时所积累的平面几何、空间几何知识进行排除则不难得出正确答案,由于时易知正三角形的三个顶点是两两距离相等的从而可以排除、,又当时易知正四面体的四个顶点也是两两距离相等的从而可以排除.
3.【2014山东.理4】 用反证法证明命题“设为实数,则方程至少有一个实根”时,要做的假设是( )
方程没有实根 B.方程至多有一个实根
C.方程至多有两个实根 D.方程恰好有两个实根
【答案】
【名师点睛】本题考查反证法.解答本题关键是理解反证法的含义,明确至少有一个的反面是一个也没有.本题属于基础题,难度较小.
4.【2015高考浙江,理6】设,是有限集,定义,其中表示有限集A中的元素个数,命题①:对任意有限集,,“”是“ ”的充分必要条件;
命题②:对任意有限集,,,,( )
A. 命题①和命题②都成立 B. 命题①和命题②都不成立
C. 命题①成立,命题②不成立 D. 命题①不成立,命题②成立
【答案】A.
【解析】命题①显然正确,通过如下文氏图亦可知表示的区域不大于
的区域,故命题②也正确,故选A.
【考点定位】集合的性质
【名师点睛】本题是集合的阅读材料题,属于中档题,在解题过程中需首先理解材料中相关概念与已知的集合相关知识点的结合,即可知命题①正确,同时注重数形结合思想的运用,若用韦恩图表示三个集合,,,则可将问题等价转化为比较集合区域的大小,即可确定集合中元素个数大小的比较.
5. 【2014年.浙江卷.理8】记,,设为平面向量,则( )
A.
B.
C.
D.
答案:D
解析:根据向量运算的几何意义,即三角形法则,可知与的大小不确定,由平行四边形法则及余弦定理可知,所对的角大于或等于,故,故选D
考点:向量运算的几何意义.
【名师点睛】本题在处理时要结合着向量加减法的几何意义,将 放在同一个平行四边形中进行比较判断,在具体解题时,本题采用了排除法,对错误选项进行举反例说明,这是高考中做选择题的常用方法,也不失为一种快速有效的方法,在高考选择题的处理上,未必每一题都要写出具体解答步骤,针对选择题的特点,有时“排除法”,“确定法”,“特殊值”代入法等也许是一种更快速,更有
有效的方法.
6. 【2014高考北京理第8题】学生的语文、数学成绩均被评为三个等级,依次为“优秀”“合格”“不合格”.若学生甲的语文、数学成绩都不低于学生乙,且其中至少有一门成绩高于乙,则称“学生甲比学生乙成绩好”.如果一组学生中没有哪位学生比另一位学生成绩好,并且不存在语文成绩相同、数学成绩也相同的两位学生,那么这组学生最多有( )
A.2人 B.3人 C.4人 D.5人
【答案】B
【解析】
考点:合情推理,中等题.
【名师点睛】本题考查计数问题,本题属于基础题,但要求学生对题目中“学生甲比学生乙成绩好”这个定义要读懂,还考查学生的分析问题的能力.
7. 【2015高考北京,理8】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D.某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
【答案】D
考点:本题考点定位为函数应用问题,考查学生对新定义“燃油效率”的理解和对函数图象的理解.
【名师点睛】本题考查对新定义“燃油效率”的理解和读图能力,本题属于中等题,有能力要求,贴近学生生活,要求按照“燃油效率”的定义,汽车每消耗1升汽油行驶的里程,可以断定“燃油效率”高的车省油,相同的速度条件下,“燃油效率”高的汽车,每消耗1升汽油行驶的里程必然大,需要学生针对四个选择只做出正确判断.
8.【2014年普通高等学校招生全国统一考试湖北卷6】若函数、满足,则称、在区间上的一组正交函数,给出三组函数:①;②;③.
其中为区间的正交函数的组数是( )
A.0 B.1 C.2 D.3
【答案】C
【解析】
所以满足条件的正交函数有2组,故选C.
考点:新定义题型,微积分基本定理的运用,容易题.
【名师点睛】以高等数学中的正交函数为载体,重点考查微积分基本定理的应用,充分体现了数学基础知识的应用能力,能较好的考查学生识记和理解数学基本概念的能力、基础知识在实际问题中的运用能力以及较强的数学计算能力.
9. 【2014年普通高等学校招生全国统一考试湖北卷8】《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,令相承也.又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长与高,计算其体积的近似公式它实际上是将圆锥体积公式中的圆周率近似取为3.那么近似公式相当于将圆锥体积公式中的近似取为( )
B. C. D.
【答案】B
【解析】
试题分析:设圆锥底面圆的半径为,高为,依题意,,,
所以,即的近似值为,故选B.
考点:《算数书》中的近似计算,容易题.
【名师点睛】以数学史为背景,重点考查圆锥的体积计算问题,其解题的关键是读懂文字材料,正确理解题意,建立方程关系.充分体现了方程思想在实际问题中的应用,能较好的考查学生运用基础知识的能力和简单近似计算能力.
10. 【2015高考湖北,理9】已知集合,,定义集合,则中元素的个数为( )
A.77 B.49 C.45 D.30
【答案】C
【解析】因为集合,所以集合中有9个元素(即9个点),即图中圆中的整点,集合中有25个元素(即25个点):即图中正方形中的整点,集合的元素可看作正方形中的整点(除去四个顶点),即个.
【考点定位】1.集合的相关知识,2.新定义题型.
【名师点睛】新定义题型的特点是:通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题情景,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的.
二、填空题
1. 【2014课标Ⅰ,理14】甲、乙、丙三位同学被问到是否去过三个城市时,
甲说:我去过的城市比乙多,但没去过城市;
乙说:我没去过城市.
丙说:我们三个去过同一城市.
由此可判断乙去过的城市为__________
【答案】A
【解析】由丙说可知,乙至少去过A,B,C中的一个城市,由甲说可知,甲去过A,C且比乙去过的城市多,故乙只去过一个城市,且没去过C城市,故乙只去过A城市.
【考点定位】推理.
【名师点睛】本题主要考查了命题的逻辑分析、简单的合情推理, 题目设计巧妙,解题时要抓住关键,逐步推断,本题主要考查考生分析问题,解决问题的能力.
2. 【2014山东.理15】已知函数,对函数,定义关于的对称函数为函数,满足:对于任意,两个点关于点对称,若是关于的“对称函数”,且恒成立,则实数的取值范围是_________.
【答案】
【名师点睛】本题考查阅读理解能力、学习能力、运算能力、直线与圆的位置关系.解答本题的关键,是理解新定义运算,将问题转化成恒成立,利用数形结合思想,再将问题转化成直线与圆的位置关系问题.
本题属于新定义问题,是一道创新能力题,中等难度之上.在考查阅读理解能力、学习能力、运算能力、直线与圆的位置关系等的同时,考查转化与化归思想及数形结合思想.
3. 【2015高考山东,理11】观察下列各式:
……
照此规律,当nN时,
.
【答案】
【解析】因为第一个等式右端为: ;第二个等式右端为: ;第三个等式右端为: 由归纳推理得:第 个等式为: 所以答案应填:
【考点定位】1、合情推理;2、组合数.
【名师点睛】本题考查了合情推理与组合数,重点考查了学生对归纳推理的理解与运用,意在考查学生观察、分析、归纳、推理判断的能力,关键是能从前三个特殊的等式中观察、归纳、总结出一般的规律,从而得到结论.此题属基础题.
4. 【2016高考新课标2理数】有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是 .
【答案】1和3
【解析】
试题分析:由题意分析可知甲的卡片上数字为1和3,乙的卡片上数字为2和3,丙卡片上数字为1和2.
考点: 逻辑推理.
【名师点睛】逻辑推理即演绎推理,就是从一般性的前提出发,通过推导即“演绎”,得出具体陈述或个别结论的过程.演绎推理的逻辑形式对于理性的重要意义在于,它对人的思维保持严密性、一贯性有着不可替代的校正作用.逻辑推理包括演绎、归纳和溯因三种方式.
5. 【2014高考陕西版理第14题】观察分析下表中的数据:
多面体
面数()
顶点数()
棱数()
三棱锥
5
6
9
五棱锥
6
6
10
立方体
6
8
12
猜想一般凸多面体中,所满足的等式是_________.
【答案】
【解析】
考点:归纳推理.
【名师点晴】本题主要考查的是归纳推理,属于中档题,解题时注意观察,归纳三棱锥、五棱锥、立方体等几何体面数()、顶点数()、棱数()之间的关系,归纳猜想一般凸多面体中,所满足的等式.当然,如果平时能够记忆这个关系,则可以得到事半功倍的效果
6.【2014四川,理15】以表示值域为R的函数组成的集合,表示具有如下性质的函数组成的集合:对于函数,存在一个正数,使得函数的值域包含于区间.例如,当,时,,.现有如下命题:
①设函数的定义域为,则“”的充要条件是“,,”;
②函数的充要条件是有最大值和最小值;
③若函数,的定义域相同,且,,则;
④若函数(,)有最大值,则.
其中的真命题有 .(写出所有真命题的序号)
【答案】①③④
【解析】
试题分析:对①,若对任意的,都,使得,则的值域必为R;反之,的值域为R,则对任意的,都,使得.故正确.
对②,比如函数属于B,但是它既无最大值也无最小值.故错误.
对③,因为,而有界,故,所以 .故正确.
对④,.当或时,均无最大值.所以若有最大值,则,此时,.故正确.
【考点定位】1、新定义;2、函数的定义域值域.
【名师点睛】新定义问题一般先考察对定义的理解,这时只需一一验证定义中各个条件即可.二是考查满足新定义的函数的简单应用,如在某些条件下,满足新定义的函数有某些新的性质,这也是在新环境下研究“旧”性质,此时需结合新函数的新性质,探究“旧”性质.三是考查综合分析能力,主要将新性质有机应用在“旧”性质,创造性证明更新的性质.
7. 【2014年普通高等学校招生全国统一考试湖北卷14】设是定义在上的函数,且,对任意,若经过点,的直线与轴的交点为,则称为关于函数的平均数,记为,例如,当时,可得,即为的算术平均数.
当时,为的几何平均数;
当时,为的调和平均数;
(以上两空各只需写出一个符合要求的函数即可)
【答案】(1);(2).
【解析】
故可以选择.
考点:两个数的几何平均数与调和平均数,难度中等.新定义型试题是高考的热点试题,考生错误往往有二,其一为不能正确理解题意,将新问题转化为所熟悉的数学问题;其二,不具备归纳、猜想、推理、传化等数学能力.但纵观湖北近四年高考试题,新定义型试题是必考试题,在专题复习中应加强训练.
【名师点睛】以新定义为背景,以函数为依托,重点考查两个数的几何平均数与调和平均数,涉及构造函数,充分体现了函数思想在高中数学中的重要地位,其易错点有二,其一为不能正确理解题意,将新问题转化为所熟悉的数学问题;其二,不具备归纳、猜想、推理、传化等数学能力.
8.【2015高考福建,理15】一个二元码是由0和1组成的数字串 ,其中 称为第位码元,二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0),已知某种二元码 的码元满足如下校验方程组:
其中运算 定义为:.
现已知一个这种二元码在通信过程中仅在第 位发生码元错误后变成了1101101,那么利用上述校验方程组可判定 等于 .
【答案】.
【考点定位】推理证明和新定义.
【名师点睛】本题以二元码为背景考查新定义问题,解决时候要耐心读题,并分析新定义的特点,按照所给的数学规则和要求进行逻辑推理和计算等,从而达到解决问题的目的,.
三、解答题
1. 【2014高考北京理第20题】(本小题满分13分)
对于数对序列,记,,其中表示和两个数中最大的数.
(1)对于数对序列,求的值;
(2)记为,,,四个数中最小的数,对于由两个数对组成的数对序列和,试分别对和两种情况比较和的大小;
(3)在由五个数对组成的所有数对序列中,写出一个数对序列使最小,并写出的值.(只需写出结论).
【答案】(1)7,8;(2)无论还是,都有成立;(3),,,,.
【解析】
试题分析:根据条件中的定义,对于数对序列,记,,其中表示和两个数中最大的数,求解.
试题解析:依题意,,
.
(2),
,
当时,,
因为,且,
所以,
当时,,
因为,且,
所以,
所以无论还是,都有成立.
(3)数对序列:(4,6),(11,11),(16,11),(11,8),(5,2)的值最小.
,,,,.
考点:新定义题型.
【名师点睛】近年北京卷理科压轴题一直为新信息题,本题考查学生对新定义的理解能力和使用能力,本题属于偏难问题,反映出学生对于新的信息的的理解和接受能力,题目给出新的定义:并对定义中max{Tk-1(P),a1+a2+…+ak}做出解释,第一步尝试对于数对序列P:(2,5),(4,1)使用定义,求得T1(P),T2(P),初步使用定义,加深对定义的理解,第二步中的比较大小及第三步中的求最值就是在第一步的基础上的深化研究,毕竟是一个新的信息题,在一个全新的环境下进行思维,所以学生做起来还是很费力的.
2. 【2015高考北京,理20】已知数列满足:,,且.
记集合.
(Ⅰ)若,写出集合的所有元素;
(Ⅱ)若集合存在一个元素是3的倍数,证明:的所有元素都是3的倍数;
(Ⅲ)求集合的元素个数的最大值.
【答案】(1),(2)证明见解析,(3)8
【解析】(Ⅰ)由已知可知:
(Ⅱ)因为集合存在一个元素是3的倍数,所以不妨设是3的倍数,由已知,可用用数学归纳法证明对任意,是3的倍数,当时,则M中的所有元素都是3的倍数,如果时,因为或,所以是3的倍数,于是是3的倍数,类似可得,都是3的倍数,从而对任意,是3的倍数,因此的所有元素都是3的倍数.
(Ⅲ)由于中的元素都不超过36,由,易得,类似可得,其次中的元素个数最多除了前面两个数外,都是4的倍数,因为第二个数必定为偶数,由的定义可知,第三个数及后面的数必定是4的倍数,另外,M中的数除以9的余数,由定义可知,和除以9的余数一样,
①若中有3的倍数,由(2)知:所有的都是3的倍数,所以都是3的倍数,所以除以9的余数为为3,6,3,6,...... ,或6,3,6,3......,或0,0,0,...... ,而除以9余3且是4的倍数只有12,除以9余6且是4的倍数只有24,除以9余0且是4的倍数只有36,则M中的数从第三项起最多2项,加上前面两项,最多4项.
考点定位:1.分段函数形数列通项公式求值;2.归纳法证明;3.数列元素分析.
【名师点睛】本题考查数列的有关知识及归纳法证明方法,即考查了数列(分段形函数)求值,又考查了归纳法证明和对数据的分析研究,考查了学生的分析问题能力和逻辑推理能力,本题属于拔高难题,特别是第二、三两步难度较大,适合选拔优秀学生.
3. 【2014上海,理22】(本题满分16分)本题共3个小题,第1小题满分3分,第2小题满分5分,第3小题满分8分.
在平面直角坐标系中,对于直线:和点记若<0,则称点被直线分隔.若曲线C与直线没有公共点,且曲线C上存在点被直线分隔,则称直线为曲线C的一条分隔线.
⑴ 求证:点被直线分隔;
⑵若直线是曲线的分隔线,求实数的取值范围;
⑶动点M到点的距离与到轴的距离之积为1,设点M的轨迹为E,求证:通过原点的直线中,有且仅有一条直线是E的分割线.
【答案】(1)证明见解析;(2);(3)证明见解析.
【解析】
试题分析:本题属于新定义问题,(1)我们只要利用题设定义求出的值,若,则结论就可得证;(2)直线是曲线的分隔线,首先直线与曲线无交点,即直线方程与曲线方程联立方程组,方程组应无实解,方程组变形为,此方程就无实解,注意分类讨论,按二次项系数为0和不为0分类,然后在曲线上找到两点位于直线的两侧.则可得到所求范围;(3)首先求出轨迹的方程,化简为,过原点的直线中,当斜率存在时设其方程为,然后解方程组,变形为,这个方程有无实数解,直接判断不方便,可转化为判断函数与的图象有无交点,而这可利用函数图象直接判断.是开口方向向上的二次函数,是幂函数,其图象一定有交点,因此直线不是的分隔线,过原点的直线还有一条就是,它显然与曲线无交点,又曲线上两点一定在直线两侧,故它是分隔线,结论得证.
试题解析:(1)由题得,,∴被直线分隔.
(2)由题得,直线与曲线无交点
即无解
∴或,∴.
又对任意的,点和在曲线上,满足,被直线分隔,所以所求的范围是.
(3)由题得,设,∴,
化简得,点的轨迹方程为
①当过原点的直线斜率存在时,设方程为.
联立方程,.
令,因为,
所以方程有实解,直线与曲线有交点.直线不是曲线的分隔线.
【考点】新定义,直线与曲线的公共点问题.
【名师点睛】判断直线l与圆锥曲线C的位置关系时,通常将直线l的方程Ax+By+C=0(A,B不同时为0)代入圆锥曲线C的方程F(x,y)=0,消去y(也可以消去x)得到一个关于变量x(或变量y)的一元方程.
即消去y,得ax2+bx+c=0.
(1)当a≠0时,设一元二次方程ax2+bx+c=0的判别式为Δ,则Δ>0?直线与圆锥曲线C相交;
Δ=0?直线与圆锥曲线C相切;
Δ<0?直线与圆锥曲线C相离.
(2)当a=0,b≠0时,即得到一个一次方程,则直线l与圆锥曲线C相交,且只有一个交点,此时,若C为双曲线,则直线l与双曲线的渐近线的位置关系是平行;若C为抛物线,则直线l与抛物线的对称轴的位置关系是平行或重合.
1.归纳法
2.类比法
3.数学归纳法
4.分析法
5.综合法
6.反证法
7.三段论
【知识要点】
1.合情推理
归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,统称为合情推理.
当前提为真时,结论可能为真的推理叫合情推理.数学中常见的合情推理有:归纳和类比推理.
(1)根据某类事物的部分对象具有的某些特征推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理,称为归纳推理(简称归纳).简言之,归纳推理是由部分到整体、由个别到一般的推理.
(2)由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理 (简称类比).简言之,类比推理是由特殊到特殊的推理.
2.演绎推理
(1)定义:演绎推理是根据已有的事实和正确的结论(包括定义、公理、定理等),按照严格的逻辑法则得到新结论的推理过程,简言之,演绎推理是由一般到特殊的推理.
(2)演绎推理的一般模式——“三段论”
①大前提——已知的一般性的原理;
②小前提——所研究的特殊情况;
③结论——根据一般原理,对特殊情况做出的判断.
1.合情推理主要包括归纳推理和类比推理
在数学研究中,在得到一个新结论前,合情推理能帮助猜测和发现结论.证明一个数学结论之前,合情推理常常能为证明提供思路与方向.
2.合情推理的过程
→→→
3.演绎推理
演绎推理是从一般性的原理出发,推出某个特殊情况的结论的推理方法.是由一般到特殊的推理,常用的一般模式是三段论.数学问题的证明主要通过演绎推理来进行.
4.注意归纳和类比的结论的可靠性有待于证明.
1.直接证明
(1)从原命题的条件逐步推得命题成立的证明称为直接证明.综合法和分析法是直接证明中最基本的两种证明方法,也是解决数学问题时常用的思维方法.
(2)从已知条件出发,以已知的定义、公理、定理为依据,逐步下推,直到推出要证明的结论为止.这种证明方法常称为综合法.
推证过程如下:
→→→…→
(3)从要证明的结论出发,追溯导致结论成立的充分条件,逐步上溯,直到使结论成立的条件和已知条件或已知事实吻合为止.这种证明方法常称为分析法.
推论过程如下:
→→→…→得到一个明显成立的条件.
P—表示条件,Q—表示要证的结论.
2.间接证明——反证法
(1)假设原命题不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立,这样的证明方法叫做反证法.
(2)反证法的特点:先假设原命题不成立,再在正确的推理下得出矛盾,所得矛盾可以是与已知条件矛盾,或与假设矛盾,或与定义、公理、定理、事实矛盾等.
推论过程如下:
→→→…→得到一个明显成立的条件.
P—表示条件,Q—表示要证的结论.
2.间接证明——反证法
(1)假设原命题不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立,这样的证明方法叫做_________.
(2)反证法的特点:先假设原命题__________成立,再在正确的推理下得出矛盾,所得矛盾可以是与已知条件矛盾,或与假设矛盾,或与定义、公理、定理、事实矛盾等.
2.关于反证法
使用反证法证明的关键是在正确的推理下得出矛盾,这个矛盾可以是与已知条件矛盾,或与假设矛盾,或与定义、公理、定理、公式、事实矛盾等.
反证法的步骤:(1)反设;(2)推出矛盾;(3)下结论.
矛盾的主要类型:(1)与假设矛盾;(2)与数学公式、法则、公理、定理、定义或已被证明了的结论矛盾;(3)与公认的简单事实矛盾;(4)自相矛盾.
1.数学归纳法是专门证明与正整数集有关的命题的一种方法.它是一种完全归纳法,是对不完全归纳法的完善.
2.证明代数恒等式的关键是第二步,将式子转化成与归纳假设的结构相同的形式——凑假设,然后利用归纳假设,经过恒等变形,得到结论所需要的形式——凑结论.
3.用数学归纳法证明不等式的关键是第二步,利用证明不等式的方法(如放缩)把式子化为n=k+1成立时的式子.
4.用数学归纳法证明几何问题时,要注意结合几何图形的性质,在求由“n=k到n=k+1”增加的元素个数时,可以先用不完全归纳法找其变化规律.
5.由有限个特殊事例进行归纳、猜想,而得出一般性结论,然后加以证明是科学研究的重要思想方法,研究与正整数有关的数学问题,此方法尤为重要,如猜想数列的通项an或前n项和Sn,解决与自然数有关的探索性、开放性问题等.这里猜想必须准确,证明必须正确.既用到合情推理,又用到演绎推理.猜想的准确与否可用证明来检验,否则不妨再分析,再猜想,再证明,猜想是证明的前提,证明可论证猜想的可靠性,二者相辅相成.
二.命题类型演练和命题陷阱
1.归纳法
例1已知数列满足, ,则( )
A. B. C. D.
【答案】A
【解析】数列满足, , ,
,由此猜想,故选A.
练习1.将正整数排成下表:
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
……………
则在表中数字2017出现在( )
A. 第44行第80列 B. 第45行第80列 C. 第44行第81列 D. 第45行第81列
【答案】D
【解析】因为每行的最后一个数分别为1,4,9,16,…,所以由此归纳出第n行的最后一个数为n2.
因为442=1936,452=2025,
所以2017出现在第45行上.
又由2017﹣1936=81,
故2017出现在第81列,
故选:D
练习2. 《聊斋志异》中有这样一首诗:“挑水砍柴不堪苦,请归但求穿墙术. 得诀自诩无所阻,额上坟起终不悟.”在这里,我们称形如以下形式的等式具有“穿墙术”: , ,则按照以上规律,若具有 “穿墙术”,则n=
A. 35 B. 48 C. 63 D. 80
【答案】C
练习3.图一是美丽的“勾股树”,它是一个直角三角形分别以它的每一边向外作正方形而得到.图二是第1代“勾股树”,重复图二的作法,得到图三为第2代“勾股树”,以此类推,已知最大的正方形面积为1,则第代“勾股树”所有正方形的面积的和为( )
A. B. C. D.
【答案】D
【解析】最大的正方形面积为1,当n=1时,由勾股定理知正方形面积的和为2,依次类推,可得所有正方形面积的和为,选D.
练习4.九章算术》“少广”算法中有这样一个数的序列:列出“全步”(整数部分)及诸分子分母,以最下面的分母遍乘各分子和“全步”,各自以分母去约其分子,将所得能通分之分数进行通分约简,又用最下面的分母去遍乘诸(未通者)分子和以通之数,逐个照此同样方法,直至全部为整数,例如: 及时,如图:
记为每个序列中最后一列数之和,则为( )
A. 1089 B. 680 C. 840 D. 2520
【答案】A
【解析】当时,序列如图:
故练习5. 如图所示为计算机科学中的蛇形模型,则第20行从左到右第4个数字为__________.
【答案】194
练习6.观察下列等式:1=++;1=+++;1=++++;…,以此类推,1=++++++,其中n∈N*.则n=________.
【答案】12
【解析】1=+(-)+,1=+(-)+(-)+,
1=+(-)+(-)+(-)+,…,以此类推,
故1=+(-)+(-)+(-)+(-)+(-)+
=++++++,故n=12.
故答案为:12
【规律方法总结】:归纳推理的一般步骤: 一、通过观察个别情况发现某些相同的性质. 二、从已知的相同性质中推出一个明确表述的一般性命题(猜想). 常见的归纳推理分为数的归纳和形的归纳两类:(1) 数的归纳包括数的归纳和式子的归纳,解决此类问题时,需要细心观察,寻求相邻项及项与序号之间的关系,同时还要联系相关的知识,如等差数列、等比数列等;(2) 形的归纳主要包括图形数目的归纳和图形变化规律的归纳.
练习7. 某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.
(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
【答案】(1)(2)见解析
【解析】(1).
(2)三角恒等式:.
证明如下:左边
2.类比法
例2. 二维空间中,圆的一维测度(周长),二维测度(面积),三维空间中,球的二维测度(表面积),三维测度(体积),应用合情推理,若四维空间中,“超球”的三维测度,则其思维测度W=( )
A. B. C. D.
【答案】A
练习1. 如图所示,由曲线y=x2,直线x=a,x=a+1(a>0)及x轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即.运用类比推理,若对?n∈N*, 恒成立,则实数A=________.
【答案】
【解析】令,
依据类比推理可得A1=dx=ln(n+1)-lnn,A2=dx=ln(n+2)-ln(n+1),…,An=dx=ln(2n)-ln(2n-1),所以A=A1+A2+…+An=ln(n+1)-lnn+ln(n+2)-ln(n+1)+…+ln(2n)-ln(2n-1)=ln(2n)-lnn=ln 2.
练习2. 我国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一直角边为股,斜边为弦.若a,b,c为直角三角形的三边,其中c为斜边,则a2+b2=c2,称这个定理为勾股定理.现将这一定理推广到立体几何中:在四面体O-ABC中,∠AOB=∠BOC=∠COA=90°,S为顶点O所对面的面积,S1,S2,S3分别为侧面△OAB,△OAC,△OBC的面积,则下列选项中对于S,S1,S2,S3满足的关系描述正确的为( )
A. S2=S+S+S B.
C. S=S1+S2+S3 D.
【答案】A
【解析】如图,作OD⊥BC于点D,连接AD,由立体几何知识知,AD⊥BC,从而S2=(BC·AD)2=BC2·AD2=BC2·(OA2+OD2)= (OB2+OC2)·OA2+BC2·OD2=(OB·OA)2+(OC·OA)2+(BC·OD)2=.
练习3. 对于问题“已知关于x的不等式ax2+bx+c>0的解集为(-1,2),解关于x的不等式ax2-bx+c>0”,给出如下一种解法:
由ax2+bx+c>0的解集为(-1,2),得a(-x)2+b(-x)+c>0的解集为(-2,1),即关于x的不等式ax2-bx+c>0的解集为(-2,1).
思考上述解法,若关于x的不等式的解集为,则关于x的不等式的解集为( )
A. (-3,-1)∪(1,2) B. (1,2)
C. (-1,2) D. (-3,2)
【答案】A
【解析】由关于x的不等式的解集为,得的解集为(-3,-1)∪(1,2),即关于x的不等式的解集为(-3,-1)∪(1,2).
练习3. .已知数列{an}为等差数列,若am=a,an=b(n-m≥1,m,n∈N*),则.类比上述结论,对于等比数列{bn}(bn>0,n∈N*),若bm=c,bn=d(n-m≥2,m,n∈N*),则可以得到bm+n等于( )
A. B.
C. D.
【答案】C
【解析】观察{an}的性质: ,则联想nb-ma对应等比数列{bn}中的,
而{an}中除以(n-m)对应等比数列中开(n-m)次方,故bm+n=.
练习4. 中国有个名句“运筹帷幄之中,决胜千里之外”.其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算.算筹的摆放形式有纵横两种形式.如图,表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推,例如用算筹表示就是,则用算筹表示为( )
A. B.
C. D.
【答案】B
故答案为:B。
练习5. 的三边长分别为, 的面积为,内切圆半径为,则;类比这个结论可知: 四面体的四个面的面积分别为,内切球的半径为,四面体的体积为, ( )
A. B.
C. D.
【答案】C
【解析】
3.数学归纳法
例3. 1.下面四个判断中,正确的是( )
A. 式子,当时为1
B. 式子 ,当时为
C. 式子,当时为
D. 设,则
【答案】C
【解析】对于A,当n=1时,f(k)恒为1+k,错误;
对于B,当n=1时,f(k)恒为1,错误;
对于C,当n=1时,f(n)为,正确;
对于D,f(k+1)=f(k)+﹣,错误;
故选:C.
练习1. 用数学归纳法证明时,从“
到”左边需增乘的代数式为( )
A. B. C. D.
【答案】D
练习2. 如图所示,将若干个点摆成三角形图案,每条边(包括两个端点)有n(n>1,n∈N)个点,相应的图案中总的点数记为an,则等于( )
A. B.
C. D.
【答案】C
【解析】每条边有n个点,所以3条边有3n个点,三角形的3个顶点重复计算了一次,所以减3个顶点,即an=3n-3,那么,
即 ,故选C.
4.分析法
例4. 淮北一中艺术节对摄影类的A,B,C,D四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是C或D作品获得一等奖”;
乙说:“B作品获得一等奖”;
丙说:“A,D两项作品未获得一等奖”;
丁说:“是C作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是( ).
A. A作品 B. B作品 C. C作品 D. D作品
【答案】B
故选:B.
练习1. 某班有三个小组,甲、乙、丙三人分属不同的小组.某次数学考试成绩公布情况如下:甲和三人中的第3小组那位不一样,丙比三人中第1小组的那位的成绩低,三人中第3小组的那位比乙分数高。若甲、乙、丙三人按数学成绩由高到低排列,正确的是( )
A. 甲、乙、丙 B. 甲、丙、乙 C. 乙、甲、丙 D. 丙、甲、乙
【答案】B
【解析】甲和三人中的第小组那位不一样,说明甲不在第小组;三人中第小组那位比乙分数高,说明乙不在第3组,说明丙在第3组,又第3组成绩低于第1组,大于乙,这时可得乙为第2组,甲为第1组,那么成绩从高到低为:甲、丙、乙,故选B.
练习2.老师在四个不同的盒子里面放了4张不同的扑克牌,分别是红桃,梅花,方片以及黑桃,让明、小红、小张、小李四个人进行猜测:
小明说:第1个盒子里面放的是梅花,第3个盒子里面放的是方片;
小红说:第2个盒子里面饭的是梅花,第3个盒子里放的是黑桃;
小张说:第4个盒子里面放的是黑桃,第2个盒子里面放的是方片;
小李说:第4个盒子里面放的是红桃,第3个盒子里面放的是方片;
老师说:“小明、小红、小张、小李,你们都只说对了一半.”则可以推测,第4个盒子里装的是( )
A. 红桃或黑桃 B. 红桃或梅花
C. 黑桃或方片 D. 黑桃或梅花
【答案】A
【解析】因为四个人都只猜对了一半,故有一下两种可能:
(1)当小明猜对第1个盒子里面放的是梅花A时,第3个盒子里面放的不是方片A,则小李猜对第4个盒子里面放的时红桃A,小张猜对第2个盒子里面放的是方片A,小红猜对第3个盒子里面放的是黑桃A;
(2)若小明猜对的是第3个盒子里面放的是方片A,则第1个盒子里面放的不是梅花A,小红猜对第2个盒子里面放的是梅花A,小张猜对第4个盒子里面放的是黑桃A,小李猜对第3个盒子里面放的是方片A,则第一个盒子只能是红桃A,
故选A.
5.综合法
例5. 德国大数学家高斯年少成名,被誉为数学王子.19岁的高斯得到了一个数学史上非常重要的结论,就是《正十七边形尺规作图之理论与方法》, 在其年幼时,对1+2+3+…+100的求和运算中,提出了倒序相加法的原理,该原理基于所给数据前后对应项的和呈现一定的规律生成,因此,此方法也被称为高斯算法.现有函数f(x)=,则f(1)+f(2)+…+f(m+2017)等于( )
A. B. C. D.
【答案】C
【解析】f(1)+f(2)+f(3)+…+f(m+2017)=++…++,
又f(1)+f(2)+f(3)+…+f(m+2017)=++…++,
两式相加可得f(1)+f(2)+f(3)+…+f(m+2017)=.
故选:C
练习1. 若a,b是常数,a>0,b>0,a≠b,x,y∈(0,+∞),则,当且仅当=时取等号.利用以上结论,可以得到函数f(x)= (0
C. 25 D. 2
【答案】C
【解析】由题意可得f(x)==≥=25,
当且仅当=,即x=时取等号,故最小值为25.
故选:C
练习1. 在直角坐标平面上的一列点简记为若由构成的数列满足其中为方向与轴正方向相同的单位向量,则称为点列.有下列说法
①为点列;
②若为点列,且点在点的右上方.任取其中连续三点则可以为锐角三角形;
③若为点列,正整数若,满足则
④若为点列,正整数若,满足则.
其中,正确说法的个数为()
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】①由题意可知, ,显然有是点列,①正确;②在中, , , 点在点的右上方, 为点列, , ,则, 为钝角, 为钝角三角形, 不可以为锐角三角形,②错;
③, ,
,③正确;
④同理②, 由于为点列,于是,可推导, ,即,④正确,正确说法的个数为,故选C.
6.反证法
例6.(1)用分析法证明:当, 时, ;
(2)证明:对任意, , , 这个值至少有一个不小于.
【答案】(1)见解析;(2)见解析
(2)假设这3个值没有一个不小于0,
即
则,(*)
而.
这与(*)矛盾,所以假设不成立,即原命题成立.
【点睛】
分析法是“执果索因”,是寻找命题成立的充分条件,如果条件成立的话,则命题成立。
反证法是,假设命题的结论不成立,即反面成立,再根据假设及条件及己知公式定理,推出与条件或定理公理或已知事实矛盾的结论,即假设不成立,原命题成立。
练习1.已知,则下列三个数 ( )
A. 都大于6 B. 至少有一个不大于6
C. 都小于6 D. 至少有一个不小于6
【答案】D
【解析】设都小于6,
则++<18,
利用基本不等式可得+ ≥2+2+2=4+8+6=18,
这与假设所得结论矛盾,故假设不成立,
故下列三个数至少有一个不小于6,
故选:D
2.已知,则下列三个数 ( )
A. 都大于6 B. 至少有一个不大于6
C. 都小于6 D. 至少有一个不小于6
【答案】D
【解析】设都大于6,
则++<18,
利用基本不等式可得+ ≥2+2+2=4+8+6=18,
这与假设所得结论矛盾,故假设不成立,
故下列三个数至少有一个不小于6,
故选:D
3.① 已知,求证,用反证法证明时,可假设;② 设为实数, ,求证与中至少有一个不小于,有反证法证明时可假设,且,以下说法正确的是( )
A. ①与②的假设都错误 B. ①与②的假设都正确
C. ①的假设正确,②的假设错误 D. ①的假设错误,②的假设正确
【答案】C
【解析】①用反证法证明时,假设命题为假,应为全面否定,所以的假命题应为,故①的假设正确;②与中至少有一个不小于的否定为与中都小于,故②的假设错误;故选C.
4.设、、都是正数,则、、三个数( )
A. 都大于 B. 都小于 C. 至少有一个大于 D. 至少有一个不小于
【答案】D
【解析】假设、、三个数都小于,则:
,
利用均值不等式的结论有:
得到矛盾的结论,可见假设不成立,
即、、三个数中至少有一个不小于.
本题选择D选项.
【方法总结】:用反证法证明不等式要把握三点:(1)必须先否定结论,即肯定结论的反面;(2)必须从否定结论进行推理,即应把结论的反面作为条件,且必须依据这一条件进行推证;(3)推导出的矛盾可能多种多样,有的与已知矛盾,有的与假设矛盾,有的与已知事实矛盾等,且推导出的矛盾必须是明显的.
5.用反证法证明命题:“,若可被整除,那么中至少有一个能被整除.”时,假设的内容应该是
A. 都能被5整除 B. 都不能被5整除
C. 不都能被5整除 D. 能被5整除
【答案】B
6.⑴当时,求证: ;
⑵已知, .试证明至少有一个不小于.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:
⑴由,
当时,可得,即可证明结论;
⑵可用反证法:假设都小于,即,可得,
进而,即可得到矛盾,即可作出证明.
试题解析:
⑴
∵ ∴
∴
⑵假设都小于,即
则有 ①
而 ②
①与②矛盾
故至少有一个不小于.
7.已知是数列的前项和,并且,对任意正整数, ,设().
(1)证明:数列是等比数列,并求的通项公式;
(2)设,求证:数列不可能为等比数列.
【答案】(1)答案见解析;(2)证明见解析.
∴bn=an+1-2an,
∴bn+1=an+2-2an+1=4(an+1-an)-2an+1,bn+1=2(an+1-2an)=2bn(n∈N*),
∴,∴{bn}是以2为公比的等比数列,
∵b1=a2-2a1,而a1+a2=4a1+2,∴a2=3a1+2=5,b1=5-2=3,
∴bn=3?2n-1(n∈N*)
(II),假设为等比数列,则有
, n≥2, 则有=0
与 ≥1矛盾,所以假设不成立,则原结论成立,即
数列不可能为等比数列
8.(1)若都是正实数,且,求证: 与中至少有一个成立。
(2)求证:
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)本题证明结论中结构较复杂,而其否定结构简单,故可用反证法证明其否定不成立,以此来证明结论成立.(2)采用分析法从要证的结果入手去证明不等式即可。
解析:
(1)假设<2和<2都不成立,即≥2和≥2同时成立. ∵x>0且y>0,∴1+x≥2y,且1+y≥2x.
两式相加得2+x+y≥2x+2y,∴x+y≤2.这与已知条件x+y>2矛盾,
∴<2和<2中至少有一个成立.
(2)原式子等价于2,两边平方得到 ,得证。
9.证明: 不是有理数.
【解析】试题分析:利用反证法假设是有理数,进而利用有理数的性质分析得出矛盾,进而得出答案.
试题解析:
假设为有理数
那么存在两个互质的正整数,使得: ,
于是,两边平方得
由是偶数,可得是偶数.
而只有偶数的平方才是偶数,所以也是偶数.
因此可设, 是正整数,代入上式,得: ,即.
所以也是偶数,这样都是偶数,不互质,这与假设互质矛盾.
因此不是有理数.
7.三段论
例7. 有一段“三段论”推理是这样的:
对于可导函数f(x),如果f′(x0)=0,那么x=x0是函数f(x)的极值点,因为函数f(x)=x3在x=0处的导数值f′(0)=0,所以x=0是函数f(x)=x3的极值点.以上推理中( )
A. 小前提错误 B. 大前提错误
C. 推理形式错误 D. 结论正确
【答案】B
【解析】大前提:如果f′(x0)=0,那么x=x0是函数f(x)的极值点,错误.
练习1. 推理过程:“因为无理数是无限小数, 是无限小数,所以是无理数”,以下说法正确的是( )
A. 完全归纳推理,结论正确 B. 三段论推理,结论正确
C. 传递性关系推理,结论正确 D. 大前提正确,推出的结论错误
【答案】D
故选:D.
三.高考真题演练
1. 【2017课标II,理7】甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩。老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩。看后甲对大家说:我还是不知道我的成绩。根据以上信息,则( )
A.乙可以知道四人的成绩 B.丁可以知道四人的成绩
C.乙、丁可以知道对方的成绩 D.乙、丁可以知道自己的成绩
【答案】D
【解析】
故选D。
【考点】合情推理
【名师点睛】合情推理主要包括归纳推理和类比推理。数学研究中,在得到一个新结论前,合情推理能帮助猜测和发现结论,在证明一个数学结论之前,合情推理常常能为证明提供思路与方向。合情推理仅是“合乎情理”的推理,它得到的结论不一定正确。而演绎推理得到的结论一定正确(前提和推理形式都正确的前提下)。
2.【2015高考广东,理8】若空间中个不同的点两两距离都相等,则正整数的取值( )
A.大于5 B. 等于5 C. 至多等于4 D. 至多等于3
【答案】.
【解析】显然正三角形和正四面体的顶点是两两距离相等的,即或时命题成立,由此可排除、、,故选.
【考点定位】空间想象能力,推理能力,含有量词命题真假的判断.
【名师点睛】本题主要考查学生的空间想象能力,推理求解能力和含有量词命题真假的判断,此题属于中高档题,如果直接正面解答比较困难,考虑到是选择题及选项信息可以根据平时所积累的平面几何、空间几何知识进行排除则不难得出正确答案,由于时易知正三角形的三个顶点是两两距离相等的从而可以排除、,又当时易知正四面体的四个顶点也是两两距离相等的从而可以排除.
3.【2014山东.理4】 用反证法证明命题“设为实数,则方程至少有一个实根”时,要做的假设是( )
方程没有实根 B.方程至多有一个实根
C.方程至多有两个实根 D.方程恰好有两个实根
【答案】
【名师点睛】本题考查反证法.解答本题关键是理解反证法的含义,明确至少有一个的反面是一个也没有.本题属于基础题,难度较小.
4.【2015高考浙江,理6】设,是有限集,定义,其中表示有限集A中的元素个数,命题①:对任意有限集,,“”是“ ”的充分必要条件;
命题②:对任意有限集,,,,( )
A. 命题①和命题②都成立 B. 命题①和命题②都不成立
C. 命题①成立,命题②不成立 D. 命题①不成立,命题②成立
【答案】A.
【解析】命题①显然正确,通过如下文氏图亦可知表示的区域不大于
的区域,故命题②也正确,故选A.
【考点定位】集合的性质
【名师点睛】本题是集合的阅读材料题,属于中档题,在解题过程中需首先理解材料中相关概念与已知的集合相关知识点的结合,即可知命题①正确,同时注重数形结合思想的运用,若用韦恩图表示三个集合,,,则可将问题等价转化为比较集合区域的大小,即可确定集合中元素个数大小的比较.
5. 【2014年.浙江卷.理8】记,,设为平面向量,则( )
A.
B.
C.
D.
答案:D
解析:根据向量运算的几何意义,即三角形法则,可知与的大小不确定,由平行四边形法则及余弦定理可知,所对的角大于或等于,故,故选D
考点:向量运算的几何意义.
【名师点睛】本题在处理时要结合着向量加减法的几何意义,将 放在同一个平行四边形中进行比较判断,在具体解题时,本题采用了排除法,对错误选项进行举反例说明,这是高考中做选择题的常用方法,也不失为一种快速有效的方法,在高考选择题的处理上,未必每一题都要写出具体解答步骤,针对选择题的特点,有时“排除法”,“确定法”,“特殊值”代入法等也许是一种更快速,更有
有效的方法.
6. 【2014高考北京理第8题】学生的语文、数学成绩均被评为三个等级,依次为“优秀”“合格”“不合格”.若学生甲的语文、数学成绩都不低于学生乙,且其中至少有一门成绩高于乙,则称“学生甲比学生乙成绩好”.如果一组学生中没有哪位学生比另一位学生成绩好,并且不存在语文成绩相同、数学成绩也相同的两位学生,那么这组学生最多有( )
A.2人 B.3人 C.4人 D.5人
【答案】B
【解析】
考点:合情推理,中等题.
【名师点睛】本题考查计数问题,本题属于基础题,但要求学生对题目中“学生甲比学生乙成绩好”这个定义要读懂,还考查学生的分析问题的能力.
7. 【2015高考北京,理8】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D.某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
【答案】D
考点:本题考点定位为函数应用问题,考查学生对新定义“燃油效率”的理解和对函数图象的理解.
【名师点睛】本题考查对新定义“燃油效率”的理解和读图能力,本题属于中等题,有能力要求,贴近学生生活,要求按照“燃油效率”的定义,汽车每消耗1升汽油行驶的里程,可以断定“燃油效率”高的车省油,相同的速度条件下,“燃油效率”高的汽车,每消耗1升汽油行驶的里程必然大,需要学生针对四个选择只做出正确判断.
8.【2014年普通高等学校招生全国统一考试湖北卷6】若函数、满足,则称、在区间上的一组正交函数,给出三组函数:①;②;③.
其中为区间的正交函数的组数是( )
A.0 B.1 C.2 D.3
【答案】C
【解析】
所以满足条件的正交函数有2组,故选C.
考点:新定义题型,微积分基本定理的运用,容易题.
【名师点睛】以高等数学中的正交函数为载体,重点考查微积分基本定理的应用,充分体现了数学基础知识的应用能力,能较好的考查学生识记和理解数学基本概念的能力、基础知识在实际问题中的运用能力以及较强的数学计算能力.
9. 【2014年普通高等学校招生全国统一考试湖北卷8】《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,令相承也.又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长与高,计算其体积的近似公式它实际上是将圆锥体积公式中的圆周率近似取为3.那么近似公式相当于将圆锥体积公式中的近似取为( )
B. C. D.
【答案】B
【解析】
试题分析:设圆锥底面圆的半径为,高为,依题意,,,
所以,即的近似值为,故选B.
考点:《算数书》中的近似计算,容易题.
【名师点睛】以数学史为背景,重点考查圆锥的体积计算问题,其解题的关键是读懂文字材料,正确理解题意,建立方程关系.充分体现了方程思想在实际问题中的应用,能较好的考查学生运用基础知识的能力和简单近似计算能力.
10. 【2015高考湖北,理9】已知集合,,定义集合,则中元素的个数为( )
A.77 B.49 C.45 D.30
【答案】C
【解析】因为集合,所以集合中有9个元素(即9个点),即图中圆中的整点,集合中有25个元素(即25个点):即图中正方形中的整点,集合的元素可看作正方形中的整点(除去四个顶点),即个.
【考点定位】1.集合的相关知识,2.新定义题型.
【名师点睛】新定义题型的特点是:通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题情景,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的.
二、填空题
1. 【2014课标Ⅰ,理14】甲、乙、丙三位同学被问到是否去过三个城市时,
甲说:我去过的城市比乙多,但没去过城市;
乙说:我没去过城市.
丙说:我们三个去过同一城市.
由此可判断乙去过的城市为__________
【答案】A
【解析】由丙说可知,乙至少去过A,B,C中的一个城市,由甲说可知,甲去过A,C且比乙去过的城市多,故乙只去过一个城市,且没去过C城市,故乙只去过A城市.
【考点定位】推理.
【名师点睛】本题主要考查了命题的逻辑分析、简单的合情推理, 题目设计巧妙,解题时要抓住关键,逐步推断,本题主要考查考生分析问题,解决问题的能力.
2. 【2014山东.理15】已知函数,对函数,定义关于的对称函数为函数,满足:对于任意,两个点关于点对称,若是关于的“对称函数”,且恒成立,则实数的取值范围是_________.
【答案】
【名师点睛】本题考查阅读理解能力、学习能力、运算能力、直线与圆的位置关系.解答本题的关键,是理解新定义运算,将问题转化成恒成立,利用数形结合思想,再将问题转化成直线与圆的位置关系问题.
本题属于新定义问题,是一道创新能力题,中等难度之上.在考查阅读理解能力、学习能力、运算能力、直线与圆的位置关系等的同时,考查转化与化归思想及数形结合思想.
3. 【2015高考山东,理11】观察下列各式:
……
照此规律,当nN时,
.
【答案】
【解析】因为第一个等式右端为: ;第二个等式右端为: ;第三个等式右端为: 由归纳推理得:第 个等式为: 所以答案应填:
【考点定位】1、合情推理;2、组合数.
【名师点睛】本题考查了合情推理与组合数,重点考查了学生对归纳推理的理解与运用,意在考查学生观察、分析、归纳、推理判断的能力,关键是能从前三个特殊的等式中观察、归纳、总结出一般的规律,从而得到结论.此题属基础题.
4. 【2016高考新课标2理数】有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是 .
【答案】1和3
【解析】
试题分析:由题意分析可知甲的卡片上数字为1和3,乙的卡片上数字为2和3,丙卡片上数字为1和2.
考点: 逻辑推理.
【名师点睛】逻辑推理即演绎推理,就是从一般性的前提出发,通过推导即“演绎”,得出具体陈述或个别结论的过程.演绎推理的逻辑形式对于理性的重要意义在于,它对人的思维保持严密性、一贯性有着不可替代的校正作用.逻辑推理包括演绎、归纳和溯因三种方式.
5. 【2014高考陕西版理第14题】观察分析下表中的数据:
多面体
面数()
顶点数()
棱数()
三棱锥
5
6
9
五棱锥
6
6
10
立方体
6
8
12
猜想一般凸多面体中,所满足的等式是_________.
【答案】
【解析】
考点:归纳推理.
【名师点晴】本题主要考查的是归纳推理,属于中档题,解题时注意观察,归纳三棱锥、五棱锥、立方体等几何体面数()、顶点数()、棱数()之间的关系,归纳猜想一般凸多面体中,所满足的等式.当然,如果平时能够记忆这个关系,则可以得到事半功倍的效果
6.【2014四川,理15】以表示值域为R的函数组成的集合,表示具有如下性质的函数组成的集合:对于函数,存在一个正数,使得函数的值域包含于区间.例如,当,时,,.现有如下命题:
①设函数的定义域为,则“”的充要条件是“,,”;
②函数的充要条件是有最大值和最小值;
③若函数,的定义域相同,且,,则;
④若函数(,)有最大值,则.
其中的真命题有 .(写出所有真命题的序号)
【答案】①③④
【解析】
试题分析:对①,若对任意的,都,使得,则的值域必为R;反之,的值域为R,则对任意的,都,使得.故正确.
对②,比如函数属于B,但是它既无最大值也无最小值.故错误.
对③,因为,而有界,故,所以 .故正确.
对④,.当或时,均无最大值.所以若有最大值,则,此时,.故正确.
【考点定位】1、新定义;2、函数的定义域值域.
【名师点睛】新定义问题一般先考察对定义的理解,这时只需一一验证定义中各个条件即可.二是考查满足新定义的函数的简单应用,如在某些条件下,满足新定义的函数有某些新的性质,这也是在新环境下研究“旧”性质,此时需结合新函数的新性质,探究“旧”性质.三是考查综合分析能力,主要将新性质有机应用在“旧”性质,创造性证明更新的性质.
7. 【2014年普通高等学校招生全国统一考试湖北卷14】设是定义在上的函数,且,对任意,若经过点,的直线与轴的交点为,则称为关于函数的平均数,记为,例如,当时,可得,即为的算术平均数.
当时,为的几何平均数;
当时,为的调和平均数;
(以上两空各只需写出一个符合要求的函数即可)
【答案】(1);(2).
【解析】
故可以选择.
考点:两个数的几何平均数与调和平均数,难度中等.新定义型试题是高考的热点试题,考生错误往往有二,其一为不能正确理解题意,将新问题转化为所熟悉的数学问题;其二,不具备归纳、猜想、推理、传化等数学能力.但纵观湖北近四年高考试题,新定义型试题是必考试题,在专题复习中应加强训练.
【名师点睛】以新定义为背景,以函数为依托,重点考查两个数的几何平均数与调和平均数,涉及构造函数,充分体现了函数思想在高中数学中的重要地位,其易错点有二,其一为不能正确理解题意,将新问题转化为所熟悉的数学问题;其二,不具备归纳、猜想、推理、传化等数学能力.
8.【2015高考福建,理15】一个二元码是由0和1组成的数字串 ,其中 称为第位码元,二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0),已知某种二元码 的码元满足如下校验方程组:
其中运算 定义为:.
现已知一个这种二元码在通信过程中仅在第 位发生码元错误后变成了1101101,那么利用上述校验方程组可判定 等于 .
【答案】.
【考点定位】推理证明和新定义.
【名师点睛】本题以二元码为背景考查新定义问题,解决时候要耐心读题,并分析新定义的特点,按照所给的数学规则和要求进行逻辑推理和计算等,从而达到解决问题的目的,.
三、解答题
1. 【2014高考北京理第20题】(本小题满分13分)
对于数对序列,记,,其中表示和两个数中最大的数.
(1)对于数对序列,求的值;
(2)记为,,,四个数中最小的数,对于由两个数对组成的数对序列和,试分别对和两种情况比较和的大小;
(3)在由五个数对组成的所有数对序列中,写出一个数对序列使最小,并写出的值.(只需写出结论).
【答案】(1)7,8;(2)无论还是,都有成立;(3),,,,.
【解析】
试题分析:根据条件中的定义,对于数对序列,记,,其中表示和两个数中最大的数,求解.
试题解析:依题意,,
.
(2),
,
当时,,
因为,且,
所以,
当时,,
因为,且,
所以,
所以无论还是,都有成立.
(3)数对序列:(4,6),(11,11),(16,11),(11,8),(5,2)的值最小.
,,,,.
考点:新定义题型.
【名师点睛】近年北京卷理科压轴题一直为新信息题,本题考查学生对新定义的理解能力和使用能力,本题属于偏难问题,反映出学生对于新的信息的的理解和接受能力,题目给出新的定义:并对定义中max{Tk-1(P),a1+a2+…+ak}做出解释,第一步尝试对于数对序列P:(2,5),(4,1)使用定义,求得T1(P),T2(P),初步使用定义,加深对定义的理解,第二步中的比较大小及第三步中的求最值就是在第一步的基础上的深化研究,毕竟是一个新的信息题,在一个全新的环境下进行思维,所以学生做起来还是很费力的.
2. 【2015高考北京,理20】已知数列满足:,,且.
记集合.
(Ⅰ)若,写出集合的所有元素;
(Ⅱ)若集合存在一个元素是3的倍数,证明:的所有元素都是3的倍数;
(Ⅲ)求集合的元素个数的最大值.
【答案】(1),(2)证明见解析,(3)8
【解析】(Ⅰ)由已知可知:
(Ⅱ)因为集合存在一个元素是3的倍数,所以不妨设是3的倍数,由已知,可用用数学归纳法证明对任意,是3的倍数,当时,则M中的所有元素都是3的倍数,如果时,因为或,所以是3的倍数,于是是3的倍数,类似可得,都是3的倍数,从而对任意,是3的倍数,因此的所有元素都是3的倍数.
(Ⅲ)由于中的元素都不超过36,由,易得,类似可得,其次中的元素个数最多除了前面两个数外,都是4的倍数,因为第二个数必定为偶数,由的定义可知,第三个数及后面的数必定是4的倍数,另外,M中的数除以9的余数,由定义可知,和除以9的余数一样,
①若中有3的倍数,由(2)知:所有的都是3的倍数,所以都是3的倍数,所以除以9的余数为为3,6,3,6,...... ,或6,3,6,3......,或0,0,0,...... ,而除以9余3且是4的倍数只有12,除以9余6且是4的倍数只有24,除以9余0且是4的倍数只有36,则M中的数从第三项起最多2项,加上前面两项,最多4项.
考点定位:1.分段函数形数列通项公式求值;2.归纳法证明;3.数列元素分析.
【名师点睛】本题考查数列的有关知识及归纳法证明方法,即考查了数列(分段形函数)求值,又考查了归纳法证明和对数据的分析研究,考查了学生的分析问题能力和逻辑推理能力,本题属于拔高难题,特别是第二、三两步难度较大,适合选拔优秀学生.
3. 【2014上海,理22】(本题满分16分)本题共3个小题,第1小题满分3分,第2小题满分5分,第3小题满分8分.
在平面直角坐标系中,对于直线:和点记若<0,则称点被直线分隔.若曲线C与直线没有公共点,且曲线C上存在点被直线分隔,则称直线为曲线C的一条分隔线.
⑴ 求证:点被直线分隔;
⑵若直线是曲线的分隔线,求实数的取值范围;
⑶动点M到点的距离与到轴的距离之积为1,设点M的轨迹为E,求证:通过原点的直线中,有且仅有一条直线是E的分割线.
【答案】(1)证明见解析;(2);(3)证明见解析.
【解析】
试题分析:本题属于新定义问题,(1)我们只要利用题设定义求出的值,若,则结论就可得证;(2)直线是曲线的分隔线,首先直线与曲线无交点,即直线方程与曲线方程联立方程组,方程组应无实解,方程组变形为,此方程就无实解,注意分类讨论,按二次项系数为0和不为0分类,然后在曲线上找到两点位于直线的两侧.则可得到所求范围;(3)首先求出轨迹的方程,化简为,过原点的直线中,当斜率存在时设其方程为,然后解方程组,变形为,这个方程有无实数解,直接判断不方便,可转化为判断函数与的图象有无交点,而这可利用函数图象直接判断.是开口方向向上的二次函数,是幂函数,其图象一定有交点,因此直线不是的分隔线,过原点的直线还有一条就是,它显然与曲线无交点,又曲线上两点一定在直线两侧,故它是分隔线,结论得证.
试题解析:(1)由题得,,∴被直线分隔.
(2)由题得,直线与曲线无交点
即无解
∴或,∴.
又对任意的,点和在曲线上,满足,被直线分隔,所以所求的范围是.
(3)由题得,设,∴,
化简得,点的轨迹方程为
①当过原点的直线斜率存在时,设方程为.
联立方程,.
令,因为,
所以方程有实解,直线与曲线有交点.直线不是曲线的分隔线.
【考点】新定义,直线与曲线的公共点问题.
【名师点睛】判断直线l与圆锥曲线C的位置关系时,通常将直线l的方程Ax+By+C=0(A,B不同时为0)代入圆锥曲线C的方程F(x,y)=0,消去y(也可以消去x)得到一个关于变量x(或变量y)的一元方程.
即消去y,得ax2+bx+c=0.
(1)当a≠0时,设一元二次方程ax2+bx+c=0的判别式为Δ,则Δ>0?直线与圆锥曲线C相交;
Δ=0?直线与圆锥曲线C相切;
Δ<0?直线与圆锥曲线C相离.
(2)当a=0,b≠0时,即得到一个一次方程,则直线l与圆锥曲线C相交,且只有一个交点,此时,若C为双曲线,则直线l与双曲线的渐近线的位置关系是平行;若C为抛物线,则直线l与抛物线的对称轴的位置关系是平行或重合.
同课章节目录
