9.2 多边形的内角和与外角和同步练习
文档属性
| 名称 | 9.2 多边形的内角和与外角和同步练习 |

|
|
| 格式 | doc | ||
| 文件大小 | 453.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-24 00:00:00 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
9.2 多边形的内角和与外角和同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.由n条不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形,各边都相等,各内角也都相等的多边形称为 正多边形 . 21cnjy.com
2.n边形的内角和等于 (n-2)·180° ,外角和等于 360° .
3.一个多边形如果边数为n,那么从每一个顶点出发有(n-3)条对角线, n边形共有 条对角线. 2-1-c-n-j-y
4. 正n边形的每个内角为 ,每个外角为
基础知识和能力拓展精练
一.选择题(共11小题)
1.把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )21教育名师原创作品
A.16 B.17 C.18 D.19
2.过某个多边形一点顶点的所有对角线,将这个多边形分成了5个三角形,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
3.一个多边形的每一个内角都等于140°,那么从这个多边形的一个顶点出发的对角线的条数是( )
A.6条 B.7条 C.8条 D.9条
4.如图,已知△ABC中,∠A=75°,则∠1+∠2=( )
( http: / / www.21cnjy.com )
A.335° B.255° C.155° D.150°
5.如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=( )www.21-cn-jy.com
( http: / / www.21cnjy.com )
A.90°﹣ ( http: / / www.21cnjy.com )α B. ( http: / / www.21cnjy.com )α C.90°+ ( http: / / www.21cnjy.com )α D.360°﹣α
6.一个多边形每个外角都等于36°,则这个多边形是几边形( )
A.7 B.8 C.9 D.10
7.正十二边形的每一个内角的度数为( )
A.120° B.135° C.150° D.108°
8.下列说法中,①三角形的内角中最多有一 ( http: / / www.21cnjy.com )个钝角;②三角形的中线将三角形分成面积相等的两部分;③从n边形的一个顶点可以引(n﹣3)条对角线,把n边形分成(n﹣2)个三角形,因此,n边形的内角和是(n﹣2) 180°;④六边形的对角线有7条,正确的个数有( )
A.4个 B.3个 C.2个 D.1个
9.一个多边形的外角和等于它的内角和的 ( http: / / www.21cnjy.com ),那么它的边数是( )
A.10 B.12 C.13 D.14
10.若四边形ABCD中,∠A:∠B:∠C=1:2:4,且∠D=108°,则∠A+∠C的度数等于( )
A.108° B.180° C.144° D.216°
二.填空题(共6小题)
11.五边形的内角和为 .
12.一个n边形的内角和是720°,则n= .
13.两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB等于 度.21教育网
( http: / / www.21cnjy.com )
14.如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA= 度.
( http: / / www.21cnjy.com )
15.如图,四边形ABCD中,∠A=100 ( http: / / www.21cnjy.com )°,∠C=70°.将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B= 度.21·cn·jy·com
( http: / / www.21cnjy.com )
16.如图,用若干个全等的正五边形可以拼成一个环状,如图是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是 .www-2-1-cnjy-com
( http: / / www.21cnjy.com )
三.解答题(共6小题)
17.一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数.
18.(1)填表:
n(凸多边形的边数) 3 4 5 …
m(凸多边形中角度等于135°的内角个数的最大值)
(2)猜想给定一个正整数n,凸n边形最多有m个内角等于135°,则m与n之间有怎样的关系?
(3)取n=7验证你的猜想是否成立?如果不成立,请给出凸n边形中最多有多少个内角等于135°?并说明理由.21*cnjy*com
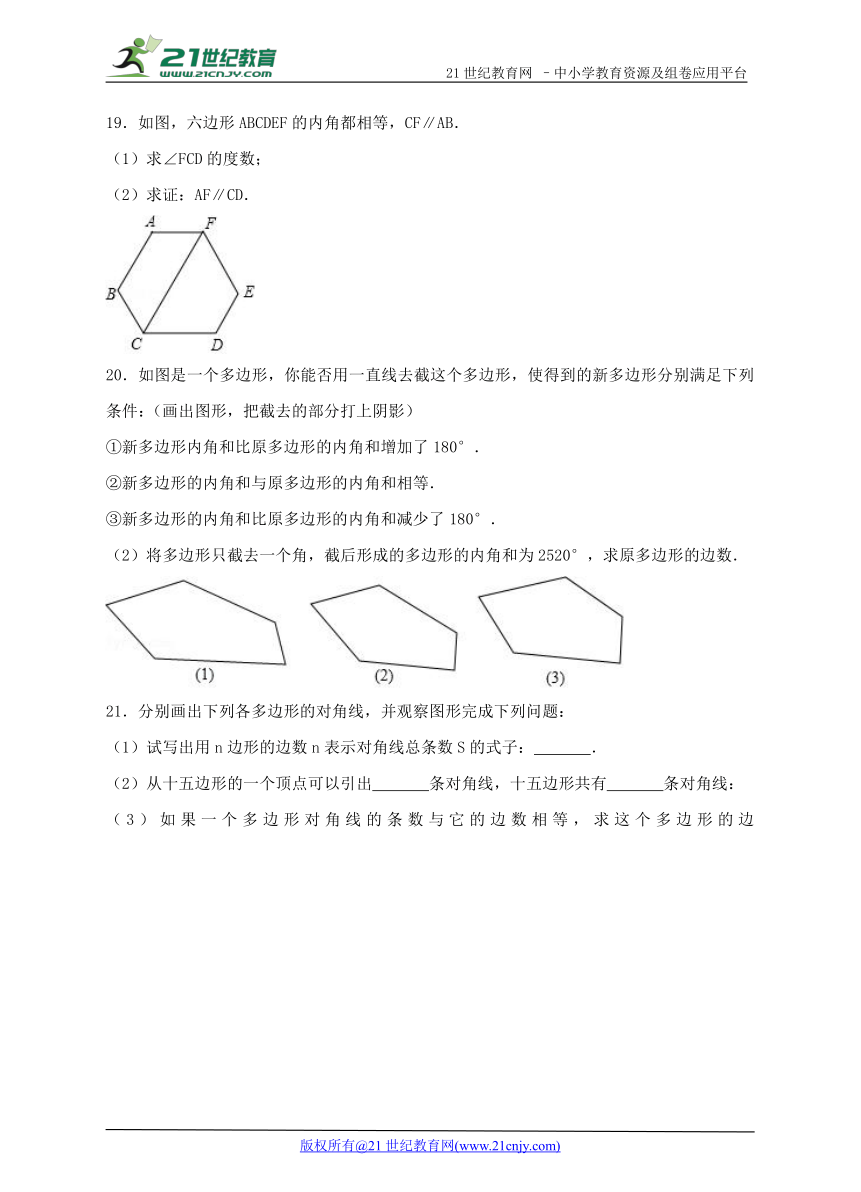
19.如图,六边形ABCDEF的内角都相等,CF∥AB.
(1)求∠FCD的度数;
(2)求证:AF∥CD.
( http: / / www.21cnjy.com )
20.如图是一个多边形,你能否用一直线去截这个多边形,使得到的新多边形分别满足下列条件:(画出图形,把截去的部分打上阴影)
①新多边形内角和比原多边形的内角和增加了180°.
②新多边形的内角和与原多边形的内角和相等.
③新多边形的内角和比原多边形的内角和减少了180°.
(2)将多边形只截去一个角,截后形成的多边形的内角和为2520°,求原多边形的边数.
( http: / / www.21cnjy.com )
21.分别画出下列各多边形的对角线,并观察图形完成下列问题:
(1)试写出用n边形的边数n表示对角线总条数S的式子: .
(2)从十五边形的一个顶点可以引出 条对角线,十五边形共有 条对角线:
(3)如果一个多边形对角线的条数与它的边数相等,求这个多边形的边数. ( http: / / www.21cnjy.com )
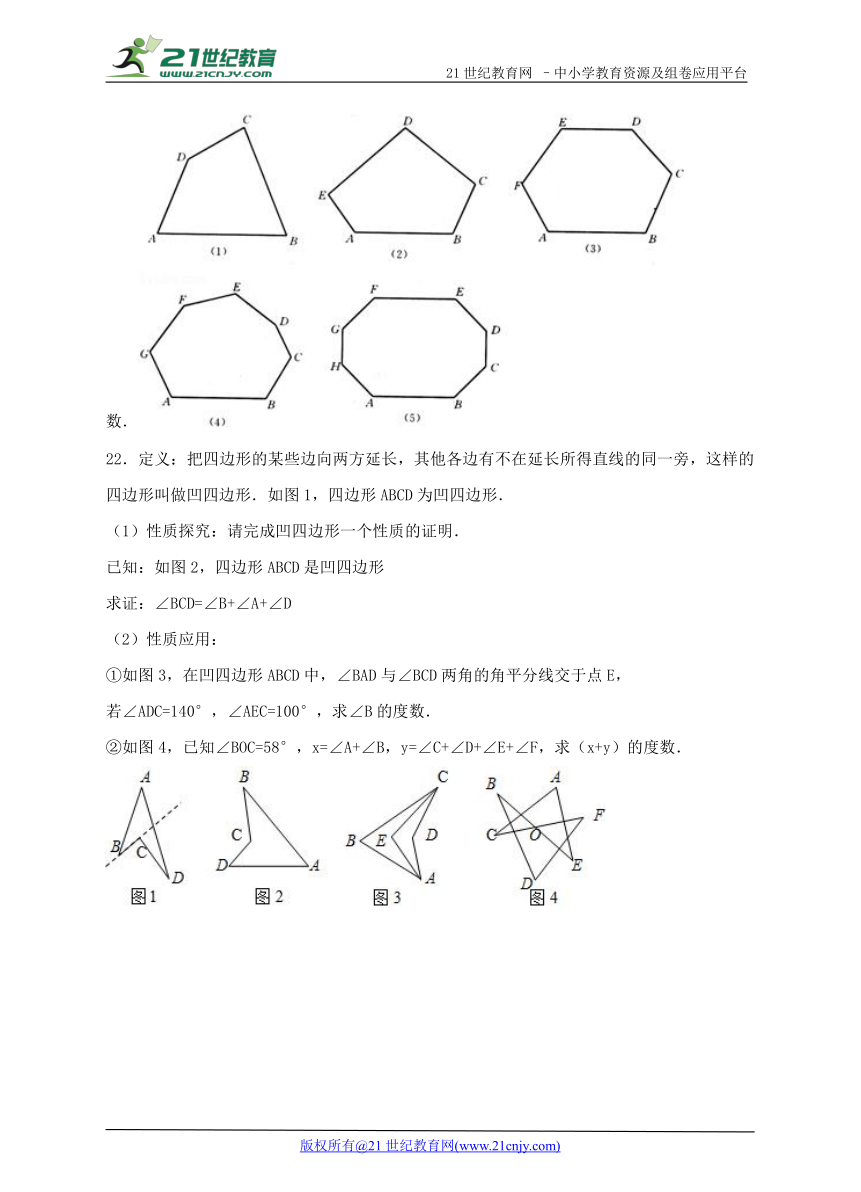
22.定义:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.如图1,四边形ABCD为凹四边形.
(1)性质探究:请完成凹四边形一个性质的证明.
已知:如图2,四边形ABCD是凹四边形
求证:∠BCD=∠B+∠A+∠D
(2)性质应用:
①如图3,在凹四边形ABCD中,∠BAD与∠BCD两角的角平分线交于点E,
若∠ADC=140°,∠AEC=100°,求∠B的度数.
②如图4,已知∠BOC=58°,x=∠A+∠B,y=∠C+∠D+∠E+∠F,求(x+y)的度数.
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共11小题)
1.
【分析】一个n边形剪去一个角后,剩下的形状可能是n边形或(n+1)边形或(n﹣1)边形.
解:当剪去一个角后,剩下的部分是一个18边形,
则这张纸片原来的形状可能是18边形或17边形或19边形,不可能是16边形.
故选:A.
2.
【分析】根据n边形从一个顶点出发可引出(n﹣3)条对角线,可组成n﹣2个三角形,依此可得n的值.
解:根据n边形从一个顶点出发可引出(n﹣3)条对角线,可组成n﹣2个三角形,
∴n﹣2=5,即n=7.
故选:C.
3.
【分析】先求出多边形的边数,再求从这个多边形的一个顶点出发的对角线的条数即可.
解:∵多边形的每一个内角都等于140°,
∴每个外角是180°﹣140°=40°,
∴这个多边形的边数是360°÷40°=9,
∴从这个多边形的一个顶点出发的对角线的条数是6条.
故选:A.
4.
【分析】先由三角形内角和定理得出∠B+∠C ( http: / / www.21cnjy.com )=180°﹣∠A=105°,再根据四边形内角和定理即可求出∠1+∠2=360°﹣105°=255°.
解:∵∠A+∠B+∠C=180°,∠A=75°,
∴∠B+∠C=180°﹣∠A=105°.
∵∠1+∠2+∠B+∠C=360°,
∴∠1+∠2=360°﹣105°=255°.
故选:B.
5.
【分析】先求出∠ABC+∠BCD的度数,然后根据角平分线的性质以及三角形的内角和定理求解∠P的度数.
解:∵四边形ABCD中,∠ABC+∠BCD=360°﹣(∠A+∠D)=360°﹣α,
∵PB和PC分别为∠ABC、∠BCD的平分线,
∴∠PBC+∠PCB= ( http: / / www.21cnjy.com )(∠ABC+∠BCD)= ( http: / / www.21cnjy.com )(360°﹣α)=180°﹣ ( http: / / www.21cnjy.com )α,
则∠P=180°﹣(∠PBC+∠PCB)=180°﹣(180°﹣ ( http: / / www.21cnjy.com )α)= ( http: / / www.21cnjy.com )α.
故选:B.
6.
【分析】多边形的外角和是360°,又有多边形的每个外角都等于36°,所以可以求出多边形外角的个数,进而得到多边形的边数.
解:这个多边形的边数是: ( http: / / www.21cnjy.com )=10.故答案是D.
7.
【分析】首先求得每个外角的度数,然后根据外角与相邻的内角互为邻补角即可求解.
解:正十二边形的每个外角的度数是: ( http: / / www.21cnjy.com )=30°,
则每一个内角的度数是:180°﹣30°=150°.
故选:C.
8.
【分析】根据三角形的内角和定理,三角形的中线的性质,对角线的定义及公式来判断所给命题是否正确即可.
解:①假设一个三角形有两个钝角,那么这两个钝角的和大于180°,与三角形的内角和为180°相矛盾.故三角形的内角中最多有一个钝角,正确;【出处:21教育名师】
②三角形的中线把三角形分成的两个三角形的底边相等,高相同,所以面积相等,正确;
③因为连接多边形不相邻的两 ( http: / / www.21cnjy.com )个顶点的线段,叫做多边形的对角线.n边形的一个顶点不能与它本身及左右两个邻点相连成对角线,故从n边形的一个顶点可以引(n﹣3)条对角线,把n边形分成(n﹣2)个三角形,每一个三角形的内角和是180°,因此,n边形的内角和是(n﹣2) 180°,正确;
④n边形共有 ( http: / / www.21cnjy.com )条对角线,所以六边形的对角线有6×3÷2=9条,错误.
故选:B.
9.
【分析】多边形的外角和是360度,多边形的外角和等于它的内角和的 ( http: / / www.21cnjy.com ),列方程求解即可.
解:∵多边形的外角和是360度,
又∵多边形的外角和等于它的内角和的 ( http: / / www.21cnjy.com ),
∴(n﹣2)×180°=6×360°,
解得:n=14
故选:D.
10.
【分析】依据∠A:∠B:∠C=1:2: ( http: / / www.21cnjy.com )4,可以设∠A是x度,则∠B是2x度,∠C是4x度,在四边形中依据内角和定理,即可得到关于x的方程,解方程就可求解.
解:∵∠A:∠B:∠C=1:2:4,
∴设∠A=x°,则∠B=2x°,∠C=4x°
在四边形ABCD中,根据内角和定理得到:x+2x+4x+108=360
解得:x=36
∴∠A=36°,∠C=144°,
∴∠A+∠C=36+144=180°.
故选:B.
二.填空题(共6小题)
11.
【分析】根据多边形的内角和公式(n﹣2) 180°计算即可.
解:(5﹣2) 180°=540°.
故答案为:540°.
12.
【分析】多边形的内角和可以表示成(n﹣2) 180°,依此列方程可求解.
解:依题意有:
(n﹣2) 180°=720°,
解得n=6.
故答案为:6.
13.
【分析】根据多边形的内角和,可得∠1,∠2,∠3,∠4,根据等腰三角形的内角和,可得∠7,根据角的和差,可得答案.2·1·c·n·j·y
解:如图 ( http: / / www.21cnjy.com ),
由正五边形的内角和,得∠1=∠2=∠3=∠4=108°,
∠5=∠6=180°﹣108°=72°,
∠7=180°﹣72°﹣72°=36°.
∠AOB=360°﹣108°﹣108°﹣36°=108°,
故答案为:108.
14.
【分析】首先求得正五边形内角∠C的度数,然后根据CD=CB求得∠CDB的度数,然后利用平行线的性质求得∠DFA的度数即可.21*cnjy*com
解:∵正五边形的外角为360°÷5=72°,
∴∠C=180°﹣72°=108°,
∵CD=CB,
∴∠CDB=36°,
∵AF∥CD,
∴∠DFA=∠CDB=36°,
故答案为:36.
15.
【分析】根据两直线平行,同位角相等 ( http: / / www.21cnjy.com )求出∠BMF,∠BNF,再根据翻折的性质求出∠BMN和∠BNM,然后利用三角形的内角和定理列式计算即可得解.【版权所有:21教育】
解:∵MF∥AD,FN∥DC,
∴∠BMF=∠A=100°,∠BNF=∠C=70°,
∵△BMN沿MN翻折得△FMN,
∴∠BMN= ( http: / / www.21cnjy.com )∠BMF= ( http: / / www.21cnjy.com )×100°=50°,
∠BNM= ( http: / / www.21cnjy.com )∠BNF= ( http: / / www.21cnjy.com )×70°=35°,
在△BMN中,∠B=180°﹣(∠BMN+∠BNM)=180°﹣(50°+35°)=180°﹣85°=95°.
故答案为:95.
16.
【分析】设要完全拼成一个圆环需要的 ( http: / / www.21cnjy.com )正五边形为n个,则围成的多边形为正n边形,利用正五边形的内角计算出正n边的每个内角的度数,然后根据内角和定理得到(n﹣2) 180°=(360°﹣2×108°)n,再解方程求出x即可.【来源:21cnj*y.co*m】
解:设要完全拼成一个圆环需要的正五边形为n个,
所以(n﹣2) 180°=(360°﹣2×108°)n,解得n=10,
所以要完全拼成一个圆环还需要的正五边形的个数为7.
故答案为7.
三.解答题(共6小题)
17.
【分析】多边形的外角和是360度,根据多边形 ( http: / / www.21cnjy.com )的内角和比它的外角和的3倍少180°,即可得到多边形的内角和的度数.根据多边形的内角和定理即可求得多边形的边数.
解:设这个多边形的边数是n,
依题意得(n﹣2)×180°=3×360°﹣180°,
n﹣2=6﹣1,
n=7.
∴这个多边形的边数是7.
18.
【分析】(1)根据三角形、四边形、五边形的内角和,可求得答案;
(2)根据(1)可猜想凸n边形中角度等于135°的内角个数的最大值为:n﹣2;
(3)设凸n边形最多有m个内角等于135°,则每个135°内角的外角都等于45°,由凸n边形的n个外角和为360°,可得k≤ ( http: / / www.21cnjy.com )=8,只有当n=8时,m才有最大值8,即可得当3≤n≤5时,凸n边形最多有n﹣2个内角等于135°;当6≤n≤7时,凸n边形最多有n﹣1个内角等于135°;当n=8时,凸n边形最多有8个内角等于135°;当n>8时,凸n边形最多有7个内角等于135°.21世纪教育网版权所有
解:(1)∵三角形中只有一个钝角,
∴三边形中角度等于135°的内角个数的最大值为1;
∵四边形的内角和为360°,
∴四边形中角度等于135°的内角个数的最大值为2;
∵五边形的内角和为540°,
∴五边形中角度等于135°的内角个数的最大值为3;
故答案为:1,2,3;
(2)由(1)得:凸n边形中角度等于135°的内角个数的最大值为:n﹣2.
即m=n﹣2;
(3)取n=7时,m=6,验证猜想不成立;
设凸n边形最多有m个内角等于135°,则每个135°内角的外角都等于45°,
∵凸n边形的n个外角和为360°,
∴k≤ ( http: / / www.21cnjy.com )=8,只有当n=8时,m才有最大值8,
讨论n≠8时的情况:
(1)当时n>8,显然,m的值是7;
(2)当n=3,4,5时,m的值分别为1,2,3;
(3)当n=6,7时,m的值分别为5,6;
综上所述,当3≤n≤5时, ( http: / / www.21cnjy.com )凸n边形最多有n﹣2个内角等于135°;当6≤n≤7时,凸n边形最多有n﹣1个内角等于135°;当n=8时,凸n边形最多有8个内角等于135°;当n>8时,凸n边形最多有7个内角等于135°.
19.
【分析】(1)先求六边形 ( http: / / www.21cnjy.com )ABCDEF的每个内角的度数,根据平行线的性质可求∠B+∠BCF=180°,再根据四边形的内角和是360°,求∠FCD的度数,从而求解.
(2)先根据四边形内角和求出∠AFC=60°,再根据平行线的判定即可求解.
解:(1)∵六边形ABCDEF的内角相等,
∴∠B=∠A=∠BCD=120°,
∵CF∥AB,
∴∠B+∠BCF=180°,
∴∠BCF=60°,
∴∠FCD=60°;
(2)∵∠AFC=360°﹣120°﹣120°﹣60°=60°,
∴∠AFC=∠FCD,
∴AF∥CD.
20.
【分析】(1)①过相邻两边上的点作出直线即可求解;
②过一个顶点和相邻边上的点作出直线即可求解;
③过相邻两边非公共顶点作出直线即可求解;
(2)根据多边形的内角和公式先求出新多边形的边数,然后再根据截去一个角的情况进行讨论.
解:(1)如图所示:
( http: / / www.21cnjy.com )
(2)设新多边形的边数为n,
则(n﹣2) 180°=2520°,
解得n=16,
①若截去一个角后边数增加1,则原多边形边数为15,
②若截去一个角后边数不变,则原多边形边数为16,
③若截去一个角后边数减少1,则原多边形边数为17,
故原多边形的边数可以为15,16或17.
21.
【分析】(1)根据多边形对角线的条数的公式即可求解;
(2)根据多边形对角线的条数的公式代值计算即可求解;
(3)根据等量关系:一个多边形对角线的条数与它的边数相等,列出方程计算即可求解.
解:如图所示:
( http: / / www.21cnjy.com )
(1)用n边形的边数n表示对角线总条数S的式子:S= ( http: / / www.21cnjy.com )n(n﹣3);
(2)十五边形从一个顶点可引出对角线:15﹣3=12(条),共有对角线: ( http: / / www.21cnjy.com )×15×(15﹣3)=90(条);【来源:21·世纪·教育·网】
(3)设多边形有n条边,
则 ( http: / / www.21cnjy.com )n(n﹣3)=n,
解得n=5或n=0(应舍去).
故这个多边形的边数是5.
故答案为:S= ( http: / / www.21cnjy.com )n(n﹣3);12,90.
22.
【分析】(1)延长BC交AD于点M,根据三角形的外角的性质即可解决问题.
(2)①利用(2)中结论如图3中,设∠B=x,∠ECB=∠ECD=α,∠EAD=∠EAB=β,列出方程组即可解决问题.21·世纪*教育网
②根据三角形的外角的性质即可得到结论.
解:(1)延长BC交AD于点M
( http: / / www.21cnjy.com )
∵∠BCD是△CDM的外角,
∴∠BCD=∠CMD+∠D,
同理∠CMD是△ABM的外角,
∴∠CMD=∠A+∠B,
∴∠BCD=∠A+∠B+∠D;
(2)①如图3,由凹四边形的性质,得∠CDA=∠E+∠EAD+∠ECD,
∵∠ADC=140°,∠AEC=100°,
∴∠EAD+∠ECD=40°.
∵∠BAD与∠BCD两角的角平分线交于点E,
∴∠BCA+∠BAC=80°,
由凹四边形的性质,得∠CDA=∠B+∠BCA+∠BAC,
∴∠B=140°﹣80°=60°.
②如图4,∵∠BOC=58°,
∴∠COE=∠BOF=122°,
由凹四边形的性质,得∠A+∠C+∠E=∠COE=122°,
∠B+∠D+∠F=∠BOF=122°,
∴∠A+∠B+∠C+∠D+∠E+∠F=122°+122°=244°.
故答案为:244°.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
9.2 多边形的内角和与外角和同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.由n条不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形,各边都相等,各内角也都相等的多边形称为 正多边形 . 21cnjy.com
2.n边形的内角和等于 (n-2)·180° ,外角和等于 360° .
3.一个多边形如果边数为n,那么从每一个顶点出发有(n-3)条对角线, n边形共有 条对角线. 2-1-c-n-j-y
4. 正n边形的每个内角为 ,每个外角为
基础知识和能力拓展精练
一.选择题(共11小题)
1.把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )21教育名师原创作品
A.16 B.17 C.18 D.19
2.过某个多边形一点顶点的所有对角线,将这个多边形分成了5个三角形,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
3.一个多边形的每一个内角都等于140°,那么从这个多边形的一个顶点出发的对角线的条数是( )
A.6条 B.7条 C.8条 D.9条
4.如图,已知△ABC中,∠A=75°,则∠1+∠2=( )
( http: / / www.21cnjy.com )
A.335° B.255° C.155° D.150°
5.如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=( )www.21-cn-jy.com
( http: / / www.21cnjy.com )
A.90°﹣ ( http: / / www.21cnjy.com )α B. ( http: / / www.21cnjy.com )α C.90°+ ( http: / / www.21cnjy.com )α D.360°﹣α
6.一个多边形每个外角都等于36°,则这个多边形是几边形( )
A.7 B.8 C.9 D.10
7.正十二边形的每一个内角的度数为( )
A.120° B.135° C.150° D.108°
8.下列说法中,①三角形的内角中最多有一 ( http: / / www.21cnjy.com )个钝角;②三角形的中线将三角形分成面积相等的两部分;③从n边形的一个顶点可以引(n﹣3)条对角线,把n边形分成(n﹣2)个三角形,因此,n边形的内角和是(n﹣2) 180°;④六边形的对角线有7条,正确的个数有( )
A.4个 B.3个 C.2个 D.1个
9.一个多边形的外角和等于它的内角和的 ( http: / / www.21cnjy.com ),那么它的边数是( )
A.10 B.12 C.13 D.14
10.若四边形ABCD中,∠A:∠B:∠C=1:2:4,且∠D=108°,则∠A+∠C的度数等于( )
A.108° B.180° C.144° D.216°
二.填空题(共6小题)
11.五边形的内角和为 .
12.一个n边形的内角和是720°,则n= .
13.两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB等于 度.21教育网
( http: / / www.21cnjy.com )
14.如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA= 度.
( http: / / www.21cnjy.com )
15.如图,四边形ABCD中,∠A=100 ( http: / / www.21cnjy.com )°,∠C=70°.将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B= 度.21·cn·jy·com
( http: / / www.21cnjy.com )
16.如图,用若干个全等的正五边形可以拼成一个环状,如图是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是 .www-2-1-cnjy-com
( http: / / www.21cnjy.com )
三.解答题(共6小题)
17.一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数.
18.(1)填表:
n(凸多边形的边数) 3 4 5 …
m(凸多边形中角度等于135°的内角个数的最大值)
(2)猜想给定一个正整数n,凸n边形最多有m个内角等于135°,则m与n之间有怎样的关系?
(3)取n=7验证你的猜想是否成立?如果不成立,请给出凸n边形中最多有多少个内角等于135°?并说明理由.21*cnjy*com
19.如图,六边形ABCDEF的内角都相等,CF∥AB.
(1)求∠FCD的度数;
(2)求证:AF∥CD.
( http: / / www.21cnjy.com )
20.如图是一个多边形,你能否用一直线去截这个多边形,使得到的新多边形分别满足下列条件:(画出图形,把截去的部分打上阴影)
①新多边形内角和比原多边形的内角和增加了180°.
②新多边形的内角和与原多边形的内角和相等.
③新多边形的内角和比原多边形的内角和减少了180°.
(2)将多边形只截去一个角,截后形成的多边形的内角和为2520°,求原多边形的边数.
( http: / / www.21cnjy.com )
21.分别画出下列各多边形的对角线,并观察图形完成下列问题:
(1)试写出用n边形的边数n表示对角线总条数S的式子: .
(2)从十五边形的一个顶点可以引出 条对角线,十五边形共有 条对角线:
(3)如果一个多边形对角线的条数与它的边数相等,求这个多边形的边数. ( http: / / www.21cnjy.com )
22.定义:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.如图1,四边形ABCD为凹四边形.
(1)性质探究:请完成凹四边形一个性质的证明.
已知:如图2,四边形ABCD是凹四边形
求证:∠BCD=∠B+∠A+∠D
(2)性质应用:
①如图3,在凹四边形ABCD中,∠BAD与∠BCD两角的角平分线交于点E,
若∠ADC=140°,∠AEC=100°,求∠B的度数.
②如图4,已知∠BOC=58°,x=∠A+∠B,y=∠C+∠D+∠E+∠F,求(x+y)的度数.
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共11小题)
1.
【分析】一个n边形剪去一个角后,剩下的形状可能是n边形或(n+1)边形或(n﹣1)边形.
解:当剪去一个角后,剩下的部分是一个18边形,
则这张纸片原来的形状可能是18边形或17边形或19边形,不可能是16边形.
故选:A.
2.
【分析】根据n边形从一个顶点出发可引出(n﹣3)条对角线,可组成n﹣2个三角形,依此可得n的值.
解:根据n边形从一个顶点出发可引出(n﹣3)条对角线,可组成n﹣2个三角形,
∴n﹣2=5,即n=7.
故选:C.
3.
【分析】先求出多边形的边数,再求从这个多边形的一个顶点出发的对角线的条数即可.
解:∵多边形的每一个内角都等于140°,
∴每个外角是180°﹣140°=40°,
∴这个多边形的边数是360°÷40°=9,
∴从这个多边形的一个顶点出发的对角线的条数是6条.
故选:A.
4.
【分析】先由三角形内角和定理得出∠B+∠C ( http: / / www.21cnjy.com )=180°﹣∠A=105°,再根据四边形内角和定理即可求出∠1+∠2=360°﹣105°=255°.
解:∵∠A+∠B+∠C=180°,∠A=75°,
∴∠B+∠C=180°﹣∠A=105°.
∵∠1+∠2+∠B+∠C=360°,
∴∠1+∠2=360°﹣105°=255°.
故选:B.
5.
【分析】先求出∠ABC+∠BCD的度数,然后根据角平分线的性质以及三角形的内角和定理求解∠P的度数.
解:∵四边形ABCD中,∠ABC+∠BCD=360°﹣(∠A+∠D)=360°﹣α,
∵PB和PC分别为∠ABC、∠BCD的平分线,
∴∠PBC+∠PCB= ( http: / / www.21cnjy.com )(∠ABC+∠BCD)= ( http: / / www.21cnjy.com )(360°﹣α)=180°﹣ ( http: / / www.21cnjy.com )α,
则∠P=180°﹣(∠PBC+∠PCB)=180°﹣(180°﹣ ( http: / / www.21cnjy.com )α)= ( http: / / www.21cnjy.com )α.
故选:B.
6.
【分析】多边形的外角和是360°,又有多边形的每个外角都等于36°,所以可以求出多边形外角的个数,进而得到多边形的边数.
解:这个多边形的边数是: ( http: / / www.21cnjy.com )=10.故答案是D.
7.
【分析】首先求得每个外角的度数,然后根据外角与相邻的内角互为邻补角即可求解.
解:正十二边形的每个外角的度数是: ( http: / / www.21cnjy.com )=30°,
则每一个内角的度数是:180°﹣30°=150°.
故选:C.
8.
【分析】根据三角形的内角和定理,三角形的中线的性质,对角线的定义及公式来判断所给命题是否正确即可.
解:①假设一个三角形有两个钝角,那么这两个钝角的和大于180°,与三角形的内角和为180°相矛盾.故三角形的内角中最多有一个钝角,正确;【出处:21教育名师】
②三角形的中线把三角形分成的两个三角形的底边相等,高相同,所以面积相等,正确;
③因为连接多边形不相邻的两 ( http: / / www.21cnjy.com )个顶点的线段,叫做多边形的对角线.n边形的一个顶点不能与它本身及左右两个邻点相连成对角线,故从n边形的一个顶点可以引(n﹣3)条对角线,把n边形分成(n﹣2)个三角形,每一个三角形的内角和是180°,因此,n边形的内角和是(n﹣2) 180°,正确;
④n边形共有 ( http: / / www.21cnjy.com )条对角线,所以六边形的对角线有6×3÷2=9条,错误.
故选:B.
9.
【分析】多边形的外角和是360度,多边形的外角和等于它的内角和的 ( http: / / www.21cnjy.com ),列方程求解即可.
解:∵多边形的外角和是360度,
又∵多边形的外角和等于它的内角和的 ( http: / / www.21cnjy.com ),
∴(n﹣2)×180°=6×360°,
解得:n=14
故选:D.
10.
【分析】依据∠A:∠B:∠C=1:2: ( http: / / www.21cnjy.com )4,可以设∠A是x度,则∠B是2x度,∠C是4x度,在四边形中依据内角和定理,即可得到关于x的方程,解方程就可求解.
解:∵∠A:∠B:∠C=1:2:4,
∴设∠A=x°,则∠B=2x°,∠C=4x°
在四边形ABCD中,根据内角和定理得到:x+2x+4x+108=360
解得:x=36
∴∠A=36°,∠C=144°,
∴∠A+∠C=36+144=180°.
故选:B.
二.填空题(共6小题)
11.
【分析】根据多边形的内角和公式(n﹣2) 180°计算即可.
解:(5﹣2) 180°=540°.
故答案为:540°.
12.
【分析】多边形的内角和可以表示成(n﹣2) 180°,依此列方程可求解.
解:依题意有:
(n﹣2) 180°=720°,
解得n=6.
故答案为:6.
13.
【分析】根据多边形的内角和,可得∠1,∠2,∠3,∠4,根据等腰三角形的内角和,可得∠7,根据角的和差,可得答案.2·1·c·n·j·y
解:如图 ( http: / / www.21cnjy.com ),
由正五边形的内角和,得∠1=∠2=∠3=∠4=108°,
∠5=∠6=180°﹣108°=72°,
∠7=180°﹣72°﹣72°=36°.
∠AOB=360°﹣108°﹣108°﹣36°=108°,
故答案为:108.
14.
【分析】首先求得正五边形内角∠C的度数,然后根据CD=CB求得∠CDB的度数,然后利用平行线的性质求得∠DFA的度数即可.21*cnjy*com
解:∵正五边形的外角为360°÷5=72°,
∴∠C=180°﹣72°=108°,
∵CD=CB,
∴∠CDB=36°,
∵AF∥CD,
∴∠DFA=∠CDB=36°,
故答案为:36.
15.
【分析】根据两直线平行,同位角相等 ( http: / / www.21cnjy.com )求出∠BMF,∠BNF,再根据翻折的性质求出∠BMN和∠BNM,然后利用三角形的内角和定理列式计算即可得解.【版权所有:21教育】
解:∵MF∥AD,FN∥DC,
∴∠BMF=∠A=100°,∠BNF=∠C=70°,
∵△BMN沿MN翻折得△FMN,
∴∠BMN= ( http: / / www.21cnjy.com )∠BMF= ( http: / / www.21cnjy.com )×100°=50°,
∠BNM= ( http: / / www.21cnjy.com )∠BNF= ( http: / / www.21cnjy.com )×70°=35°,
在△BMN中,∠B=180°﹣(∠BMN+∠BNM)=180°﹣(50°+35°)=180°﹣85°=95°.
故答案为:95.
16.
【分析】设要完全拼成一个圆环需要的 ( http: / / www.21cnjy.com )正五边形为n个,则围成的多边形为正n边形,利用正五边形的内角计算出正n边的每个内角的度数,然后根据内角和定理得到(n﹣2) 180°=(360°﹣2×108°)n,再解方程求出x即可.【来源:21cnj*y.co*m】
解:设要完全拼成一个圆环需要的正五边形为n个,
所以(n﹣2) 180°=(360°﹣2×108°)n,解得n=10,
所以要完全拼成一个圆环还需要的正五边形的个数为7.
故答案为7.
三.解答题(共6小题)
17.
【分析】多边形的外角和是360度,根据多边形 ( http: / / www.21cnjy.com )的内角和比它的外角和的3倍少180°,即可得到多边形的内角和的度数.根据多边形的内角和定理即可求得多边形的边数.
解:设这个多边形的边数是n,
依题意得(n﹣2)×180°=3×360°﹣180°,
n﹣2=6﹣1,
n=7.
∴这个多边形的边数是7.
18.
【分析】(1)根据三角形、四边形、五边形的内角和,可求得答案;
(2)根据(1)可猜想凸n边形中角度等于135°的内角个数的最大值为:n﹣2;
(3)设凸n边形最多有m个内角等于135°,则每个135°内角的外角都等于45°,由凸n边形的n个外角和为360°,可得k≤ ( http: / / www.21cnjy.com )=8,只有当n=8时,m才有最大值8,即可得当3≤n≤5时,凸n边形最多有n﹣2个内角等于135°;当6≤n≤7时,凸n边形最多有n﹣1个内角等于135°;当n=8时,凸n边形最多有8个内角等于135°;当n>8时,凸n边形最多有7个内角等于135°.21世纪教育网版权所有
解:(1)∵三角形中只有一个钝角,
∴三边形中角度等于135°的内角个数的最大值为1;
∵四边形的内角和为360°,
∴四边形中角度等于135°的内角个数的最大值为2;
∵五边形的内角和为540°,
∴五边形中角度等于135°的内角个数的最大值为3;
故答案为:1,2,3;
(2)由(1)得:凸n边形中角度等于135°的内角个数的最大值为:n﹣2.
即m=n﹣2;
(3)取n=7时,m=6,验证猜想不成立;
设凸n边形最多有m个内角等于135°,则每个135°内角的外角都等于45°,
∵凸n边形的n个外角和为360°,
∴k≤ ( http: / / www.21cnjy.com )=8,只有当n=8时,m才有最大值8,
讨论n≠8时的情况:
(1)当时n>8,显然,m的值是7;
(2)当n=3,4,5时,m的值分别为1,2,3;
(3)当n=6,7时,m的值分别为5,6;
综上所述,当3≤n≤5时, ( http: / / www.21cnjy.com )凸n边形最多有n﹣2个内角等于135°;当6≤n≤7时,凸n边形最多有n﹣1个内角等于135°;当n=8时,凸n边形最多有8个内角等于135°;当n>8时,凸n边形最多有7个内角等于135°.
19.
【分析】(1)先求六边形 ( http: / / www.21cnjy.com )ABCDEF的每个内角的度数,根据平行线的性质可求∠B+∠BCF=180°,再根据四边形的内角和是360°,求∠FCD的度数,从而求解.
(2)先根据四边形内角和求出∠AFC=60°,再根据平行线的判定即可求解.
解:(1)∵六边形ABCDEF的内角相等,
∴∠B=∠A=∠BCD=120°,
∵CF∥AB,
∴∠B+∠BCF=180°,
∴∠BCF=60°,
∴∠FCD=60°;
(2)∵∠AFC=360°﹣120°﹣120°﹣60°=60°,
∴∠AFC=∠FCD,
∴AF∥CD.
20.
【分析】(1)①过相邻两边上的点作出直线即可求解;
②过一个顶点和相邻边上的点作出直线即可求解;
③过相邻两边非公共顶点作出直线即可求解;
(2)根据多边形的内角和公式先求出新多边形的边数,然后再根据截去一个角的情况进行讨论.
解:(1)如图所示:
( http: / / www.21cnjy.com )
(2)设新多边形的边数为n,
则(n﹣2) 180°=2520°,
解得n=16,
①若截去一个角后边数增加1,则原多边形边数为15,
②若截去一个角后边数不变,则原多边形边数为16,
③若截去一个角后边数减少1,则原多边形边数为17,
故原多边形的边数可以为15,16或17.
21.
【分析】(1)根据多边形对角线的条数的公式即可求解;
(2)根据多边形对角线的条数的公式代值计算即可求解;
(3)根据等量关系:一个多边形对角线的条数与它的边数相等,列出方程计算即可求解.
解:如图所示:
( http: / / www.21cnjy.com )
(1)用n边形的边数n表示对角线总条数S的式子:S= ( http: / / www.21cnjy.com )n(n﹣3);
(2)十五边形从一个顶点可引出对角线:15﹣3=12(条),共有对角线: ( http: / / www.21cnjy.com )×15×(15﹣3)=90(条);【来源:21·世纪·教育·网】
(3)设多边形有n条边,
则 ( http: / / www.21cnjy.com )n(n﹣3)=n,
解得n=5或n=0(应舍去).
故这个多边形的边数是5.
故答案为:S= ( http: / / www.21cnjy.com )n(n﹣3);12,90.
22.
【分析】(1)延长BC交AD于点M,根据三角形的外角的性质即可解决问题.
(2)①利用(2)中结论如图3中,设∠B=x,∠ECB=∠ECD=α,∠EAD=∠EAB=β,列出方程组即可解决问题.21·世纪*教育网
②根据三角形的外角的性质即可得到结论.
解:(1)延长BC交AD于点M
( http: / / www.21cnjy.com )
∵∠BCD是△CDM的外角,
∴∠BCD=∠CMD+∠D,
同理∠CMD是△ABM的外角,
∴∠CMD=∠A+∠B,
∴∠BCD=∠A+∠B+∠D;
(2)①如图3,由凹四边形的性质,得∠CDA=∠E+∠EAD+∠ECD,
∵∠ADC=140°,∠AEC=100°,
∴∠EAD+∠ECD=40°.
∵∠BAD与∠BCD两角的角平分线交于点E,
∴∠BCA+∠BAC=80°,
由凹四边形的性质,得∠CDA=∠B+∠BCA+∠BAC,
∴∠B=140°﹣80°=60°.
②如图4,∵∠BOC=58°,
∴∠COE=∠BOF=122°,
由凹四边形的性质,得∠A+∠C+∠E=∠COE=122°,
∠B+∠D+∠F=∠BOF=122°,
∴∠A+∠B+∠C+∠D+∠E+∠F=122°+122°=244°.
故答案为:244°.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
