10.2 平移同步练习
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
10.2 平移同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.平面图形在它所在的平面上的平行移动,简称平移,它由移动的方向和移动的距离所决定.
2.平移后的图形与原来的图形的对应线段平行(有时在同一条直线上)且相等对应角相等,平移不改变图形的形状和大小 .21cnjy.com
基础知识和能力拓展精练
一.选择题(共9小题)
1.如图,A,B,C,D中的哪幅图案可以通过图案①平移得到( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
2.把图中的一个三角形先横向平移x格,再纵向平移y格,就能与另一个三角形拼合成一个四边形,那么x+y( )
( http: / / www.21cnjy.com )
A.是一个确定的值 B.有两个不同的值 C.有三个不同的值 D.有三个以上不同的值
3.如图,线段AB=CD,AB与CD相交于O,且∠AOC=60°,CE是由AB平移所得,则AC+BD与AB的大小关系是( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
A.AC+BD>AB B.AC+BD=AB C.AC+BD≥AB D.无法确定
4.某城市新建了一座游乐场,即日将完工. ( http: / / www.21cnjy.com )当施工者准备给游乐场用砖头砌上围墙时,发现在设计图纸中的某些数据已经模糊不清了(如图),从而无法计算出外围围墙的周长,因此无法备砖料.根据图中的标示,可计算出外围围墙的周长是( )【出处:21教育名师】
( http: / / www.21cnjy.com )
A.320米 B.260米 C.160米 D.100米
5.如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )【版权所有:21教育】
( http: / / www.21cnjy.com )
A.16cm B.18cm C.20cm D.21cm
6.如图,将边长为 ( http: / / www.21cnjy.com )的正方形ABCD沿对角线AC平移,使点A移至线段AC的中点A′处,得新正方形A′B′C′D′,新正方形与原正方形重叠部分(图中阴影部分)的面积是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C.1 D. ( http: / / www.21cnjy.com )
7.如图,△ABC沿着BC方向平移得到△A ( http: / / www.21cnjy.com )′B′C′,点P是直线AA′上任意一点,若△ABC,△PB′C′的面积分别为S1,S2,则下列关系正确的是( )21教育名师原创作品
( http: / / www.21cnjy.com )
A.S1>S2 B.S1<S2 C.S1=S2 D.S1=2S2
8.如图,△ABC的面积为12,将△ABC ( http: / / www.21cnjy.com )沿BC方向移到△A′B′C′的位置,使B′与C重合,连接AC′交A′C于D,则△C′DC的面积为( )21*cnjy*com
( http: / / www.21cnjy.com )
A.10 B.8 C.6 D.4
9.如图是一块长方形ABC ( http: / / www.21cnjy.com )D的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为( )
( http: / / www.21cnjy.com )
A.5050m2 B.5000m2 C.4900m2 D.4998m2
二.填空题(共7小题)
10.某景点拟在如图的矩形荷塘上架设小桥,若荷塘中小桥的总长为100米,则荷塘周长为 .
( http: / / www.21cnjy.com )
11.如图是一块从一个边长为50cm的正方形材料中剪出的垫片,现测得FG=5cm,则这个剪出的图形的周长是 cm.【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
12.如图,在一块长方形ABCD草地上 ( http: / / www.21cnjy.com ),AB=10,BC=15,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2个单位),空白部分表示的草地面积是 .
( http: / / www.21cnjy.com )
13.某宾馆在重新装修后,准备在大 ( http: / / www.21cnjy.com )厅的主楼梯上铺上红色地毯,已知这种红色地毯的售价为每平方米32元,主楼道宽2米,其侧面与正面如图所示,则购买地毯至少需要 元.
( http: / / www.21cnjy.com )
14.如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3= °.
( http: / / www.21cnjy.com )
15.如图,两个直角三角形重叠在一 ( http: / / www.21cnjy.com )起,将其中一个沿点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分的面积 .2·1·c·n·j·y
( http: / / www.21cnjy.com )
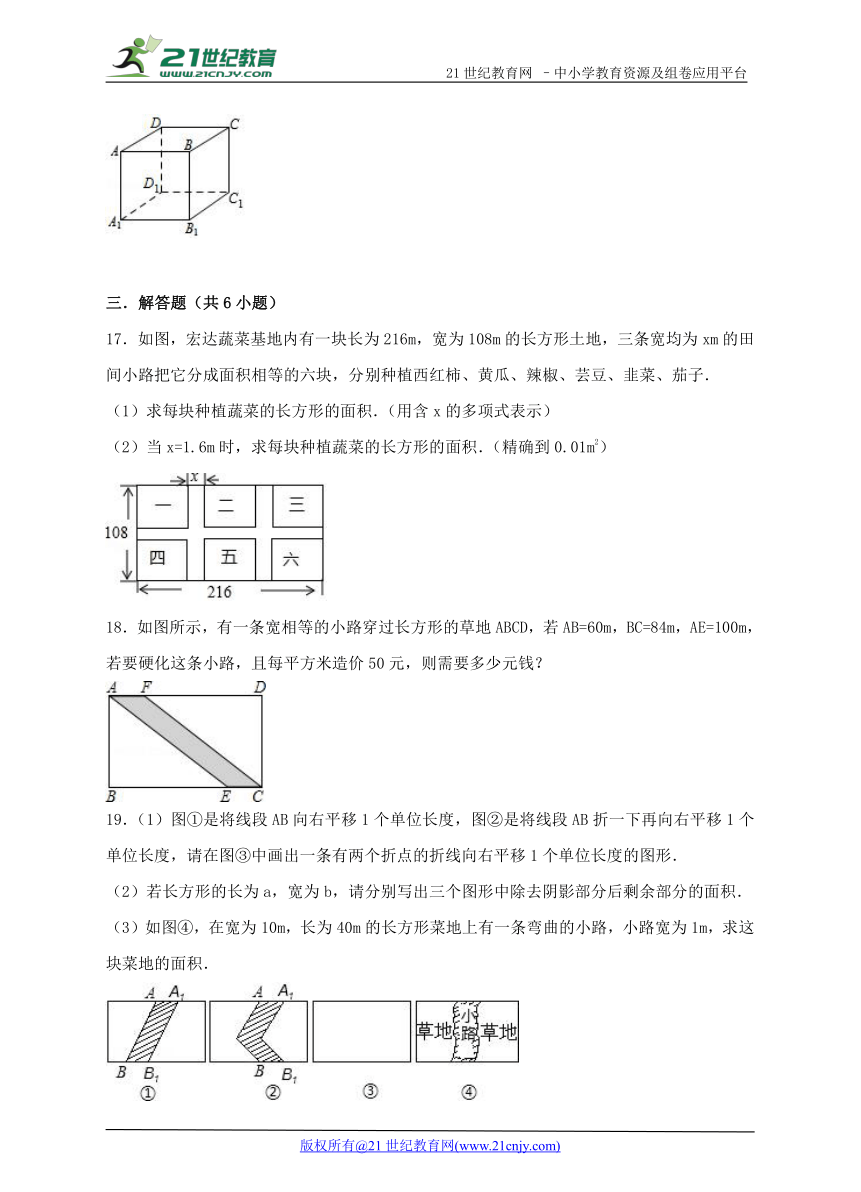
16.如图,立方体棱长为2cm,将线段AC平移到A1C1的位置上,平移的距离是 cm.
( http: / / www.21cnjy.com )
三.解答题(共6小题)
17.如图,宏达蔬菜基地内有一块长为216m ( http: / / www.21cnjy.com ),宽为108m的长方形土地,三条宽均为xm的田间小路把它分成面积相等的六块,分别种植西红柿、黄瓜、辣椒、芸豆、韭菜、茄子.
(1)求每块种植蔬菜的长方形的面积.(用含x的多项式表示)
(2)当x=1.6m时,求每块种植蔬菜的长方形的面积.(精确到0.01m2)
( http: / / www.21cnjy.com )
18.如图所示,有一条宽相 ( http: / / www.21cnjy.com )等的小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,若要硬化这条小路,且每平方米造价50元,则需要多少元钱?
( http: / / www.21cnjy.com )
19.(1)图①是将线段 ( http: / / www.21cnjy.com )AB向右平移1个单位长度,图②是将线段AB折一下再向右平移1个单位长度,请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形.
(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩余部分的面积.
(3)如图④,在宽为10m,长为40m的长方形菜地上有一条弯曲的小路,小路宽为1m,求这块菜地的面积.
( http: / / www.21cnjy.com )
20.将△ABC沿BC的方向平移得到△DEF.
(1)若∠B=74°,∠F=26°,求∠A的度数;
(2)若BC=4.5cm,EC=3.5cm,求△ABC平移的距离.
( http: / / www.21cnjy.com )
21.如图已知直线CB∥OA,∠C=∠OAB=100°,点E、点F在线段BC上,满足∠FOB=∠AOB=α,OE平分∠COF.
(1)用含有α的代数式表示∠COE的度数;
(2)若沿水平方向向右平行移动AB,则∠OBC:∠OFC的值是否发生变化?若变化找出变化规律;若不变,求其比值.
( http: / / www.21cnjy.com )
22.如图,已知MN∥PQ,B在MN上 ( http: / / www.21cnjy.com ),C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE,BE交于点E,∠CBN=120°.
(1)若∠ADQ=110°,求∠BED的度数;
(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示)
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共9小题)
1.
【分析】根据平移的性质,不改变图形的形状和大小,经过平移,对应点所连的线段平行且相等,对应线段平行且相等.
解:通过图案①平移得到必须与图案①完全相同,角度也必须相同,
观察图形可知D可以通过图案①平移得到.
故选:D.
2.
【分析】根据两个全等的直角三角形可以组成一个矩形或一个平行四边形可得出答案.
解:(1)当两斜边重合的时候可组成一个矩形,此时x=2,y=3,
x+y=5;
(2)当两直角边重合时有两种情况,①短边重合,此时x=2,y=3,x+y=5;
②长边重合,此时x=2,y=5,x+y=7.
综上可得:x+y=5或7.
故选:B.
3.
【分析】根据三角形的三边关系,及平移的基本性质可得.
解:由平移的性质知,AB与CE平行且相等,
所以四边形ACEB是平行四边形,BE=AC,
当B、D、E不共线时,
∵AB∥CE,∠DCE=∠AOC=60°,
∵AB=CE,AB=CD,
∴CE=CD,
∴△CED是等边三角形,
∴DE=AB,
根据三角形的三边关系知BE+BD=AC+BD>DE=AB,
即AC+BD>AB.
当D、B、E共线时,AC+BD=AB.
故选:C.
4.
【分析】根据图示提供的数据推知:A+B+C=50米,从而求出竖向的围墙总长度,继而表示出围墙的总长度,合并可得出答案.www.21-cn-jy.com
解:由图示提供的数据推知:A+B+C=50米,从而竖向的围墙总长度为100米,
∴从横的部分提供的数据推知,横向的围墙总长度为:50+A+30+50+30﹣A=160米,
从而外围围墙的总长度为260米.
故选:B.
5.
【分析】先根据平移的性质得到EF=AD ( http: / / www.21cnjy.com )=2cm,AE=DF,而AB+BE+AE=16cm,则四边形ABFD的周长=AB+BC+CF+DF+AD,然后利用整体代入的方法计算即可21·世纪*教育网
解:∵△ABE向右平移2cm得到△DCF,
∴EF=AD=2cm,AE=DF,
∵△ABE的周长为16cm,
∴AB+BE+AE=16cm,
∴四边形ABFD的周长=AB+BE+EF+DF+AD
=AB+BE+AE+EF+AD
=16cm+2cm+2cm
=20cm.
故选:C.
6.
【分析】根据题意可得,阴影部分的图形是正方形,正方形ABCD的边长为 ( http: / / www.21cnjy.com ),则AC=2,可得出A′C=1,可得出其面积.
解:∵正方形ABCD的边长为 ( http: / / www.21cnjy.com ),
∴AC=2,
又∵点A′是线段AC的中点,
∴A′C=1,
∴S阴影= ( http: / / www.21cnjy.com )×1×1= ( http: / / www.21cnjy.com ).
故选:B.
7.
【分析】根据平行线间的距离相等可知△ABC,△PB′C′的高相等,再由同底等高的三角形面积相等即可得到答案.
解:
∵△ABC沿着BC方向平移得到△A′B′C′,
∴AA′∥BC′,
∵点P是直线AA′上任意一点,
∴△ABC,△PB′C′的高相等,
∴S1=S2,
故选:C.
8.
【分析】根据题意,可求得D为A′B′的中点,则可知△C′DC的面积为△ABC的面积的一半.
解:∵将△ABC沿BC方向移到△A′B′C′的位置,使B′与C重合,
∴AB∥A′B′,
∵BC=CC′,
∴D为A′B′的中点,
∴△C′DC的面积为△ABC的面积的一半,即6.
故选:C.
9.
【分析】根据已知将道路平移,再利用矩形的性质求出长和宽,再进行解答.
解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:(102﹣2)米,宽为(51﹣1)米.21教育网
所以草坪的面积应该是长×宽=(102﹣2)(51﹣1)=5000(米2).
故选:B.
二.填空题(共7小题)
10.
【分析】根据图形得出荷塘中小桥的总长为矩形的长与宽的和,进而得出答案.
解:∵荷塘中小桥的总长为100米,
∴荷塘周长为:2×100=200(m)
故答案为:200m.
11.
【分析】利用平移的性质将EF,GH,AH,分别向左和上平移即可得出平移后图形,进而求出这块垫片的周长.21·cn·jy·com
解:如图所示:这块垫片的周长为:50×4+FG+NH=200+10=210(cm),
故答案为:210.
( http: / / www.21cnjy.com )
12.
【分析】根据图形列出算式,再求出即可.
解:空白部分表示的草地面积是S=10×15﹣2×10=130,
故答案为:130.
13.
【分析】根据题意,结合图形,先把楼梯的横竖向上向左平移,构成一个矩形,再求得其面积,则购买地毯的钱数可求.2-1-c-n-j-y
解:利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为5米,3米,
∴地毯的长度为5+3=8(米),
∴地毯的面积为8×2=16(平方米),
∴买地毯至少需要16×32=512(元).
故答案为:512.
14.
【分析】延长直线后根据平行线的性质和三角形的外角性质解答即可.
解:延长直线,如图: ( http: / / www.21cnjy.com ),
∵直线a平移后得到直线b,
∴a∥b,
∴∠5=180°﹣∠1=180°﹣70°=110°,
∵∠2=∠4+∠5,
∵∠3=∠4,
∴∠2﹣∠3=∠5=110°,
故答案为:110.
15.
【分析】根据平移的性质可知:AB= ( http: / / www.21cnjy.com )DE,BE=CF;由此可求出EH和CF的长.由于CH∥DF,可得出△ECH∽△EFD,根据相似三角形的对应边成比例,可求出EC的长.已知了EH、EC,DE、EF的长,即可求出△ECH和△EFD的面积,进而可求出阴影部分的面积.
解:根据题意得,DE=AB=10;BE=CF=6;CH∥DF.
∴EH=10﹣4=6;
EH:HD=EC:CF,
即 6:4=EC:6,
∴EC=9.
∴S△EFD= ( http: / / www.21cnjy.com )×10×(9+6)=75;
S△ECH= ( http: / / www.21cnjy.com )×6×9=27.
∴S阴影部分=75﹣27=48.
故答案为48.
16.
【分析】根据平移的性质即可得到结论.
解:∵将线段AC平移到A1C1的位置上,平移的距离是立方体棱长,
∴平移的距离是2cm,
故答案为:2.
三.解答题(共6小题)
17.
【分析】(1)把三条路平移到矩形的一边,求出六块总面积,即可解决问题.
(2)把问题转化为代数式求值问题.
解:(1)每块种植蔬菜的长方形的面积= ( http: / / www.21cnjy.com )(216﹣2x)(108﹣x)=3888﹣72x+ ( http: / / www.21cnjy.com )x2,
答:每块种植蔬菜的长方形的面积(3888﹣72x+ ( http: / / www.21cnjy.com )x2)m2.
(2)把x=1.6代入上式得到,
3888﹣72x+ ( http: / / www.21cnjy.com )x2=3888﹣72×1.6+ ( http: / / www.21cnjy.com )×1.62≈3773.65m2.
18.
【分析】四边形ABCD是矩形,则AF∥EC,又AF=CE,进而可判断四边形AECF的形状,继而面积可以利用底边长乘以高进行计算.21世纪教育网版权所有
解:在矩形ABCD中,AF∥EC,
又∵AF=EC,
∴四边形AECF是平行四边形.
在Rt△ABE中,AB=60,AE=100,
根据勾股定理得BE=80,
∴EC=BC﹣BE=4,
所以这条小路的面积S=EC AB=4×60=240(m2).
240×50=1200元.
答:需要1200元钱.
19.
【分析】(1)根据两个折点,可得小路是三个平行四边形;
(2)根据路的形状是矩形,可得路的面积,根据面积的和差,可得答案;
(3)根据等底等高的面积相等,可得路的面积,根据面积的和差,可得答案.
解:(1)如图:
( http: / / www.21cnjy.com );
(2)三个图形中除去阴影部分后剩余部分的面积:①ab﹣b;②ab﹣b;③ab﹣b;
(3)40×10﹣10×1=390(m2).
答:这块菜地的面积是390m2.
20.
【分析】(1)根据平移的性质求出∠2=∠F,再利用三角形的内角和等于180°列式计算即可得解;
(2)先求出BE,再根据平移的性质可得BE即为平移距离.
解:(1)由图形平移的特征可知△ABC和△DEF的形状与大小相同,
即△ABC≌△DEF,
∴∠2=∠F=26°,
∵∠B=74°,
∴∠A=180°﹣(∠2+∠B)=180°﹣(26°+74°)=80°;
(2)∵BC=4.5cm,EC=3.5cm,
∴BE=BC﹣EC=4.5﹣3.5=1cm,
∴△ABC平移的距离为1cm.
21.
【分析】(1)先根据平行线的性质得出∠C ( http: / / www.21cnjy.com )OA的度数与∠FBO=∠AOB,再由∠FOB=∠AOB,得出∠FBO=∠FOB即OB平分∠AOF,根据OE平分∠COF,可知∠EOB=∠EOF+∠FOB,故可得出结论;www-2-1-cnjy-com
(2)根据平行线的性质可得出∠OBC=∠BOA,∠OFC=∠FOA,从而得出答案.
(1)∵CB∥OA,∴∠C+∠AOC=180°.
∵∠C=100°,∴∠AOC=80°.
∴∠EOB=∠EOF+∠FOB= ( http: / / www.21cnjy.com )∠COF+ ( http: / / www.21cnjy.com )∠FOA
= ( http: / / www.21cnjy.com )(∠COF+∠FOA)= ( http: / / www.21cnjy.com )∠AOC=40°.
又OE平分∠COF,
∴∠COE=∠FOE=40°﹣α;
(2)∠OBC:∠OFC的值不发生改变.
∵BC∥OA,
∴∠FBO=∠AOB,
又∵∠BOF=∠AOB,
∴∠FBO=∠BOF,
∵∠OFC=∠FBO+∠FOB,
∴∠OFC=2∠OBC,
即∠OBC:∠OFC=∠OBC:2∠OBC=1:2= ( http: / / www.21cnjy.com ).
22.
【分析】(1)如图1中,延长DE交MN于H.利用∠BED=∠EHB+∠EBH,即可解决问题;
(2)分3种情形讨论即可解决问题.
解:(1)如图1中,延长DE交MN于H.
( http: / / www.21cnjy.com )
∵∠ADQ=110°,ED平分∠ADP,
∴∠PDH= ( http: / / www.21cnjy.com )∠PDA=35°,
∵PQ∥MN,
∴∠EHB=∠PDH=35°,
∵∠CBN=120°,EB平分∠ABC,
∴∠EBH= ( http: / / www.21cnjy.com )∠ABC=30°,
∴∠BED=∠EHB+∠EBH=65°.
(2)有3种情形,如图2中,当点E在直线MN与直线PQ之间时.延长DE交MN于H.
( http: / / www.21cnjy.com )
∵PQ∥MN,
∴∠QDH=∠DHA= ( http: / / www.21cnjy.com )n,
∴∠BED=∠EHB+∠EBH=180°﹣( ( http: / / www.21cnjy.com )n)°+30°=210°﹣( ( http: / / www.21cnjy.com )n)°,
当点E在直线MN的下方时,如图3中,设DE交MN于H.
( http: / / www.21cnjy.com )
∵∠HBA=∠ABP=30°,∠ADH=∠CDH=( ( http: / / www.21cnjy.com )n)°,
又∵∠DHB=∠HBE+∠HEB,
∴∠BED=( ( http: / / www.21cnjy.com )n)°﹣30°,
当点E在PQ上方时,如图4中,设PQ交BE于H.同法可得∠BED=30°﹣( ( http: / / www.21cnjy.com )n)°.
( http: / / www.21cnjy.com )
综上所述,∠BED=210°﹣( ( http: / / www.21cnjy.com )n)°或( ( http: / / www.21cnjy.com )n)°﹣30°或30°﹣( ( http: / / www.21cnjy.com )n)°.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
10.2 平移同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.平面图形在它所在的平面上的平行移动,简称平移,它由移动的方向和移动的距离所决定.
2.平移后的图形与原来的图形的对应线段平行(有时在同一条直线上)且相等对应角相等,平移不改变图形的形状和大小 .21cnjy.com
基础知识和能力拓展精练
一.选择题(共9小题)
1.如图,A,B,C,D中的哪幅图案可以通过图案①平移得到( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
2.把图中的一个三角形先横向平移x格,再纵向平移y格,就能与另一个三角形拼合成一个四边形,那么x+y( )
( http: / / www.21cnjy.com )
A.是一个确定的值 B.有两个不同的值 C.有三个不同的值 D.有三个以上不同的值
3.如图,线段AB=CD,AB与CD相交于O,且∠AOC=60°,CE是由AB平移所得,则AC+BD与AB的大小关系是( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
A.AC+BD>AB B.AC+BD=AB C.AC+BD≥AB D.无法确定
4.某城市新建了一座游乐场,即日将完工. ( http: / / www.21cnjy.com )当施工者准备给游乐场用砖头砌上围墙时,发现在设计图纸中的某些数据已经模糊不清了(如图),从而无法计算出外围围墙的周长,因此无法备砖料.根据图中的标示,可计算出外围围墙的周长是( )【出处:21教育名师】
( http: / / www.21cnjy.com )
A.320米 B.260米 C.160米 D.100米
5.如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )【版权所有:21教育】
( http: / / www.21cnjy.com )
A.16cm B.18cm C.20cm D.21cm
6.如图,将边长为 ( http: / / www.21cnjy.com )的正方形ABCD沿对角线AC平移,使点A移至线段AC的中点A′处,得新正方形A′B′C′D′,新正方形与原正方形重叠部分(图中阴影部分)的面积是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C.1 D. ( http: / / www.21cnjy.com )
7.如图,△ABC沿着BC方向平移得到△A ( http: / / www.21cnjy.com )′B′C′,点P是直线AA′上任意一点,若△ABC,△PB′C′的面积分别为S1,S2,则下列关系正确的是( )21教育名师原创作品
( http: / / www.21cnjy.com )
A.S1>S2 B.S1<S2 C.S1=S2 D.S1=2S2
8.如图,△ABC的面积为12,将△ABC ( http: / / www.21cnjy.com )沿BC方向移到△A′B′C′的位置,使B′与C重合,连接AC′交A′C于D,则△C′DC的面积为( )21*cnjy*com
( http: / / www.21cnjy.com )
A.10 B.8 C.6 D.4
9.如图是一块长方形ABC ( http: / / www.21cnjy.com )D的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为( )
( http: / / www.21cnjy.com )
A.5050m2 B.5000m2 C.4900m2 D.4998m2
二.填空题(共7小题)
10.某景点拟在如图的矩形荷塘上架设小桥,若荷塘中小桥的总长为100米,则荷塘周长为 .
( http: / / www.21cnjy.com )
11.如图是一块从一个边长为50cm的正方形材料中剪出的垫片,现测得FG=5cm,则这个剪出的图形的周长是 cm.【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
12.如图,在一块长方形ABCD草地上 ( http: / / www.21cnjy.com ),AB=10,BC=15,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2个单位),空白部分表示的草地面积是 .
( http: / / www.21cnjy.com )
13.某宾馆在重新装修后,准备在大 ( http: / / www.21cnjy.com )厅的主楼梯上铺上红色地毯,已知这种红色地毯的售价为每平方米32元,主楼道宽2米,其侧面与正面如图所示,则购买地毯至少需要 元.
( http: / / www.21cnjy.com )
14.如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3= °.
( http: / / www.21cnjy.com )
15.如图,两个直角三角形重叠在一 ( http: / / www.21cnjy.com )起,将其中一个沿点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分的面积 .2·1·c·n·j·y
( http: / / www.21cnjy.com )
16.如图,立方体棱长为2cm,将线段AC平移到A1C1的位置上,平移的距离是 cm.
( http: / / www.21cnjy.com )
三.解答题(共6小题)
17.如图,宏达蔬菜基地内有一块长为216m ( http: / / www.21cnjy.com ),宽为108m的长方形土地,三条宽均为xm的田间小路把它分成面积相等的六块,分别种植西红柿、黄瓜、辣椒、芸豆、韭菜、茄子.
(1)求每块种植蔬菜的长方形的面积.(用含x的多项式表示)
(2)当x=1.6m时,求每块种植蔬菜的长方形的面积.(精确到0.01m2)
( http: / / www.21cnjy.com )
18.如图所示,有一条宽相 ( http: / / www.21cnjy.com )等的小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,若要硬化这条小路,且每平方米造价50元,则需要多少元钱?
( http: / / www.21cnjy.com )
19.(1)图①是将线段 ( http: / / www.21cnjy.com )AB向右平移1个单位长度,图②是将线段AB折一下再向右平移1个单位长度,请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形.
(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩余部分的面积.
(3)如图④,在宽为10m,长为40m的长方形菜地上有一条弯曲的小路,小路宽为1m,求这块菜地的面积.
( http: / / www.21cnjy.com )
20.将△ABC沿BC的方向平移得到△DEF.
(1)若∠B=74°,∠F=26°,求∠A的度数;
(2)若BC=4.5cm,EC=3.5cm,求△ABC平移的距离.
( http: / / www.21cnjy.com )
21.如图已知直线CB∥OA,∠C=∠OAB=100°,点E、点F在线段BC上,满足∠FOB=∠AOB=α,OE平分∠COF.
(1)用含有α的代数式表示∠COE的度数;
(2)若沿水平方向向右平行移动AB,则∠OBC:∠OFC的值是否发生变化?若变化找出变化规律;若不变,求其比值.
( http: / / www.21cnjy.com )
22.如图,已知MN∥PQ,B在MN上 ( http: / / www.21cnjy.com ),C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE,BE交于点E,∠CBN=120°.
(1)若∠ADQ=110°,求∠BED的度数;
(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示)
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共9小题)
1.
【分析】根据平移的性质,不改变图形的形状和大小,经过平移,对应点所连的线段平行且相等,对应线段平行且相等.
解:通过图案①平移得到必须与图案①完全相同,角度也必须相同,
观察图形可知D可以通过图案①平移得到.
故选:D.
2.
【分析】根据两个全等的直角三角形可以组成一个矩形或一个平行四边形可得出答案.
解:(1)当两斜边重合的时候可组成一个矩形,此时x=2,y=3,
x+y=5;
(2)当两直角边重合时有两种情况,①短边重合,此时x=2,y=3,x+y=5;
②长边重合,此时x=2,y=5,x+y=7.
综上可得:x+y=5或7.
故选:B.
3.
【分析】根据三角形的三边关系,及平移的基本性质可得.
解:由平移的性质知,AB与CE平行且相等,
所以四边形ACEB是平行四边形,BE=AC,
当B、D、E不共线时,
∵AB∥CE,∠DCE=∠AOC=60°,
∵AB=CE,AB=CD,
∴CE=CD,
∴△CED是等边三角形,
∴DE=AB,
根据三角形的三边关系知BE+BD=AC+BD>DE=AB,
即AC+BD>AB.
当D、B、E共线时,AC+BD=AB.
故选:C.
4.
【分析】根据图示提供的数据推知:A+B+C=50米,从而求出竖向的围墙总长度,继而表示出围墙的总长度,合并可得出答案.www.21-cn-jy.com
解:由图示提供的数据推知:A+B+C=50米,从而竖向的围墙总长度为100米,
∴从横的部分提供的数据推知,横向的围墙总长度为:50+A+30+50+30﹣A=160米,
从而外围围墙的总长度为260米.
故选:B.
5.
【分析】先根据平移的性质得到EF=AD ( http: / / www.21cnjy.com )=2cm,AE=DF,而AB+BE+AE=16cm,则四边形ABFD的周长=AB+BC+CF+DF+AD,然后利用整体代入的方法计算即可21·世纪*教育网
解:∵△ABE向右平移2cm得到△DCF,
∴EF=AD=2cm,AE=DF,
∵△ABE的周长为16cm,
∴AB+BE+AE=16cm,
∴四边形ABFD的周长=AB+BE+EF+DF+AD
=AB+BE+AE+EF+AD
=16cm+2cm+2cm
=20cm.
故选:C.
6.
【分析】根据题意可得,阴影部分的图形是正方形,正方形ABCD的边长为 ( http: / / www.21cnjy.com ),则AC=2,可得出A′C=1,可得出其面积.
解:∵正方形ABCD的边长为 ( http: / / www.21cnjy.com ),
∴AC=2,
又∵点A′是线段AC的中点,
∴A′C=1,
∴S阴影= ( http: / / www.21cnjy.com )×1×1= ( http: / / www.21cnjy.com ).
故选:B.
7.
【分析】根据平行线间的距离相等可知△ABC,△PB′C′的高相等,再由同底等高的三角形面积相等即可得到答案.
解:
∵△ABC沿着BC方向平移得到△A′B′C′,
∴AA′∥BC′,
∵点P是直线AA′上任意一点,
∴△ABC,△PB′C′的高相等,
∴S1=S2,
故选:C.
8.
【分析】根据题意,可求得D为A′B′的中点,则可知△C′DC的面积为△ABC的面积的一半.
解:∵将△ABC沿BC方向移到△A′B′C′的位置,使B′与C重合,
∴AB∥A′B′,
∵BC=CC′,
∴D为A′B′的中点,
∴△C′DC的面积为△ABC的面积的一半,即6.
故选:C.
9.
【分析】根据已知将道路平移,再利用矩形的性质求出长和宽,再进行解答.
解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:(102﹣2)米,宽为(51﹣1)米.21教育网
所以草坪的面积应该是长×宽=(102﹣2)(51﹣1)=5000(米2).
故选:B.
二.填空题(共7小题)
10.
【分析】根据图形得出荷塘中小桥的总长为矩形的长与宽的和,进而得出答案.
解:∵荷塘中小桥的总长为100米,
∴荷塘周长为:2×100=200(m)
故答案为:200m.
11.
【分析】利用平移的性质将EF,GH,AH,分别向左和上平移即可得出平移后图形,进而求出这块垫片的周长.21·cn·jy·com
解:如图所示:这块垫片的周长为:50×4+FG+NH=200+10=210(cm),
故答案为:210.
( http: / / www.21cnjy.com )
12.
【分析】根据图形列出算式,再求出即可.
解:空白部分表示的草地面积是S=10×15﹣2×10=130,
故答案为:130.
13.
【分析】根据题意,结合图形,先把楼梯的横竖向上向左平移,构成一个矩形,再求得其面积,则购买地毯的钱数可求.2-1-c-n-j-y
解:利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为5米,3米,
∴地毯的长度为5+3=8(米),
∴地毯的面积为8×2=16(平方米),
∴买地毯至少需要16×32=512(元).
故答案为:512.
14.
【分析】延长直线后根据平行线的性质和三角形的外角性质解答即可.
解:延长直线,如图: ( http: / / www.21cnjy.com ),
∵直线a平移后得到直线b,
∴a∥b,
∴∠5=180°﹣∠1=180°﹣70°=110°,
∵∠2=∠4+∠5,
∵∠3=∠4,
∴∠2﹣∠3=∠5=110°,
故答案为:110.
15.
【分析】根据平移的性质可知:AB= ( http: / / www.21cnjy.com )DE,BE=CF;由此可求出EH和CF的长.由于CH∥DF,可得出△ECH∽△EFD,根据相似三角形的对应边成比例,可求出EC的长.已知了EH、EC,DE、EF的长,即可求出△ECH和△EFD的面积,进而可求出阴影部分的面积.
解:根据题意得,DE=AB=10;BE=CF=6;CH∥DF.
∴EH=10﹣4=6;
EH:HD=EC:CF,
即 6:4=EC:6,
∴EC=9.
∴S△EFD= ( http: / / www.21cnjy.com )×10×(9+6)=75;
S△ECH= ( http: / / www.21cnjy.com )×6×9=27.
∴S阴影部分=75﹣27=48.
故答案为48.
16.
【分析】根据平移的性质即可得到结论.
解:∵将线段AC平移到A1C1的位置上,平移的距离是立方体棱长,
∴平移的距离是2cm,
故答案为:2.
三.解答题(共6小题)
17.
【分析】(1)把三条路平移到矩形的一边,求出六块总面积,即可解决问题.
(2)把问题转化为代数式求值问题.
解:(1)每块种植蔬菜的长方形的面积= ( http: / / www.21cnjy.com )(216﹣2x)(108﹣x)=3888﹣72x+ ( http: / / www.21cnjy.com )x2,
答:每块种植蔬菜的长方形的面积(3888﹣72x+ ( http: / / www.21cnjy.com )x2)m2.
(2)把x=1.6代入上式得到,
3888﹣72x+ ( http: / / www.21cnjy.com )x2=3888﹣72×1.6+ ( http: / / www.21cnjy.com )×1.62≈3773.65m2.
18.
【分析】四边形ABCD是矩形,则AF∥EC,又AF=CE,进而可判断四边形AECF的形状,继而面积可以利用底边长乘以高进行计算.21世纪教育网版权所有
解:在矩形ABCD中,AF∥EC,
又∵AF=EC,
∴四边形AECF是平行四边形.
在Rt△ABE中,AB=60,AE=100,
根据勾股定理得BE=80,
∴EC=BC﹣BE=4,
所以这条小路的面积S=EC AB=4×60=240(m2).
240×50=1200元.
答:需要1200元钱.
19.
【分析】(1)根据两个折点,可得小路是三个平行四边形;
(2)根据路的形状是矩形,可得路的面积,根据面积的和差,可得答案;
(3)根据等底等高的面积相等,可得路的面积,根据面积的和差,可得答案.
解:(1)如图:
( http: / / www.21cnjy.com );
(2)三个图形中除去阴影部分后剩余部分的面积:①ab﹣b;②ab﹣b;③ab﹣b;
(3)40×10﹣10×1=390(m2).
答:这块菜地的面积是390m2.
20.
【分析】(1)根据平移的性质求出∠2=∠F,再利用三角形的内角和等于180°列式计算即可得解;
(2)先求出BE,再根据平移的性质可得BE即为平移距离.
解:(1)由图形平移的特征可知△ABC和△DEF的形状与大小相同,
即△ABC≌△DEF,
∴∠2=∠F=26°,
∵∠B=74°,
∴∠A=180°﹣(∠2+∠B)=180°﹣(26°+74°)=80°;
(2)∵BC=4.5cm,EC=3.5cm,
∴BE=BC﹣EC=4.5﹣3.5=1cm,
∴△ABC平移的距离为1cm.
21.
【分析】(1)先根据平行线的性质得出∠C ( http: / / www.21cnjy.com )OA的度数与∠FBO=∠AOB,再由∠FOB=∠AOB,得出∠FBO=∠FOB即OB平分∠AOF,根据OE平分∠COF,可知∠EOB=∠EOF+∠FOB,故可得出结论;www-2-1-cnjy-com
(2)根据平行线的性质可得出∠OBC=∠BOA,∠OFC=∠FOA,从而得出答案.
(1)∵CB∥OA,∴∠C+∠AOC=180°.
∵∠C=100°,∴∠AOC=80°.
∴∠EOB=∠EOF+∠FOB= ( http: / / www.21cnjy.com )∠COF+ ( http: / / www.21cnjy.com )∠FOA
= ( http: / / www.21cnjy.com )(∠COF+∠FOA)= ( http: / / www.21cnjy.com )∠AOC=40°.
又OE平分∠COF,
∴∠COE=∠FOE=40°﹣α;
(2)∠OBC:∠OFC的值不发生改变.
∵BC∥OA,
∴∠FBO=∠AOB,
又∵∠BOF=∠AOB,
∴∠FBO=∠BOF,
∵∠OFC=∠FBO+∠FOB,
∴∠OFC=2∠OBC,
即∠OBC:∠OFC=∠OBC:2∠OBC=1:2= ( http: / / www.21cnjy.com ).
22.
【分析】(1)如图1中,延长DE交MN于H.利用∠BED=∠EHB+∠EBH,即可解决问题;
(2)分3种情形讨论即可解决问题.
解:(1)如图1中,延长DE交MN于H.
( http: / / www.21cnjy.com )
∵∠ADQ=110°,ED平分∠ADP,
∴∠PDH= ( http: / / www.21cnjy.com )∠PDA=35°,
∵PQ∥MN,
∴∠EHB=∠PDH=35°,
∵∠CBN=120°,EB平分∠ABC,
∴∠EBH= ( http: / / www.21cnjy.com )∠ABC=30°,
∴∠BED=∠EHB+∠EBH=65°.
(2)有3种情形,如图2中,当点E在直线MN与直线PQ之间时.延长DE交MN于H.
( http: / / www.21cnjy.com )
∵PQ∥MN,
∴∠QDH=∠DHA= ( http: / / www.21cnjy.com )n,
∴∠BED=∠EHB+∠EBH=180°﹣( ( http: / / www.21cnjy.com )n)°+30°=210°﹣( ( http: / / www.21cnjy.com )n)°,
当点E在直线MN的下方时,如图3中,设DE交MN于H.
( http: / / www.21cnjy.com )
∵∠HBA=∠ABP=30°,∠ADH=∠CDH=( ( http: / / www.21cnjy.com )n)°,
又∵∠DHB=∠HBE+∠HEB,
∴∠BED=( ( http: / / www.21cnjy.com )n)°﹣30°,
当点E在PQ上方时,如图4中,设PQ交BE于H.同法可得∠BED=30°﹣( ( http: / / www.21cnjy.com )n)°.
( http: / / www.21cnjy.com )
综上所述,∠BED=210°﹣( ( http: / / www.21cnjy.com )n)°或( ( http: / / www.21cnjy.com )n)°﹣30°或30°﹣( ( http: / / www.21cnjy.com )n)°.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
