10.3.2 旋转的特征同步练习
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
10.3.2 旋转的特征同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.旋转的特征:
①旋转后的图形上的每一点都绕 旋转中心旋转相同的角度.
②旋转前后的图形中的对应线段、对应角都相等.
③旋转前后的图形的对应点到旋转中心的距离相等 .
2.旋转前后的旋转中心的确定:任取两对对应点,画出它们的对称轴,两对称轴的交点即为旋转中心.
基础知识和能力拓展精练
一.选择题
1.如图,△OAB绕点O逆时针旋转85°得到△OCD,若∠A=110°,∠D=40°,则∠α的度数是( )21教育网
( http: / / www.21cnjy.com )
A.35° B.45° C.55° D.65°
2.如图,将△ABC绕点A顺时针旋转 60°得到△AED,若线段AB=3,则BE=( )
( http: / / www.21cnjy.com )
A.2 B.3 C.4 D.5
3.如图,△DEF是由△ABC绕点O旋转180°而得到的,则下列结论不成立的是( )
( http: / / www.21cnjy.com )
A.点A与点D是对应点 B.BO=EO C.∠ACB=∠FDE D.AB∥DE
4.如图,在△ABC中,∠C=90°,A ( http: / / www.21cnjy.com )C=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则BE的长为( )2-1-c-n-j-y
( http: / / www.21cnjy.com )
A.1 B.2 C.3 D.4
5.如图,E、F分别是正方形ABCD的边A ( http: / / www.21cnjy.com )B、BC上的点,BE=CF,连接CE、DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转角度为( )
( http: / / www.21cnjy.com )
A.45° B.60° C.90° D.120°
6.如图,将Rt△ABC(∠B=25°)绕点A顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )【出处:21教育名师】
( http: / / www.21cnjy.com )
A.65° B.80° C.105° D.115°
7.如图,在Rt△ABC中,∠BAC=90 ( http: / / www.21cnjy.com )°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( )21教育名师原创作品
( http: / / www.21cnjy.com )
A.32° B.64° C.77° D.87°
二.填空题(共5小题)
8.如图,一块等腰直角的三 ( http: / / www.21cnjy.com )角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,使A,C,B′三点共线,那么旋转角度的大小为 .21*cnjy*com
( http: / / www.21cnjy.com )
9.如图,在△ABC中,∠BAC=60°,将△ABC绕着点A顺时针旋转40°后得到△ADE,则∠BAE= .
( http: / / www.21cnjy.com )
10.如图,在Rt△ABC中,AB=A ( http: / / www.21cnjy.com )C,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连结EF.则∠EAF= .
( http: / / www.21cnjy.com )
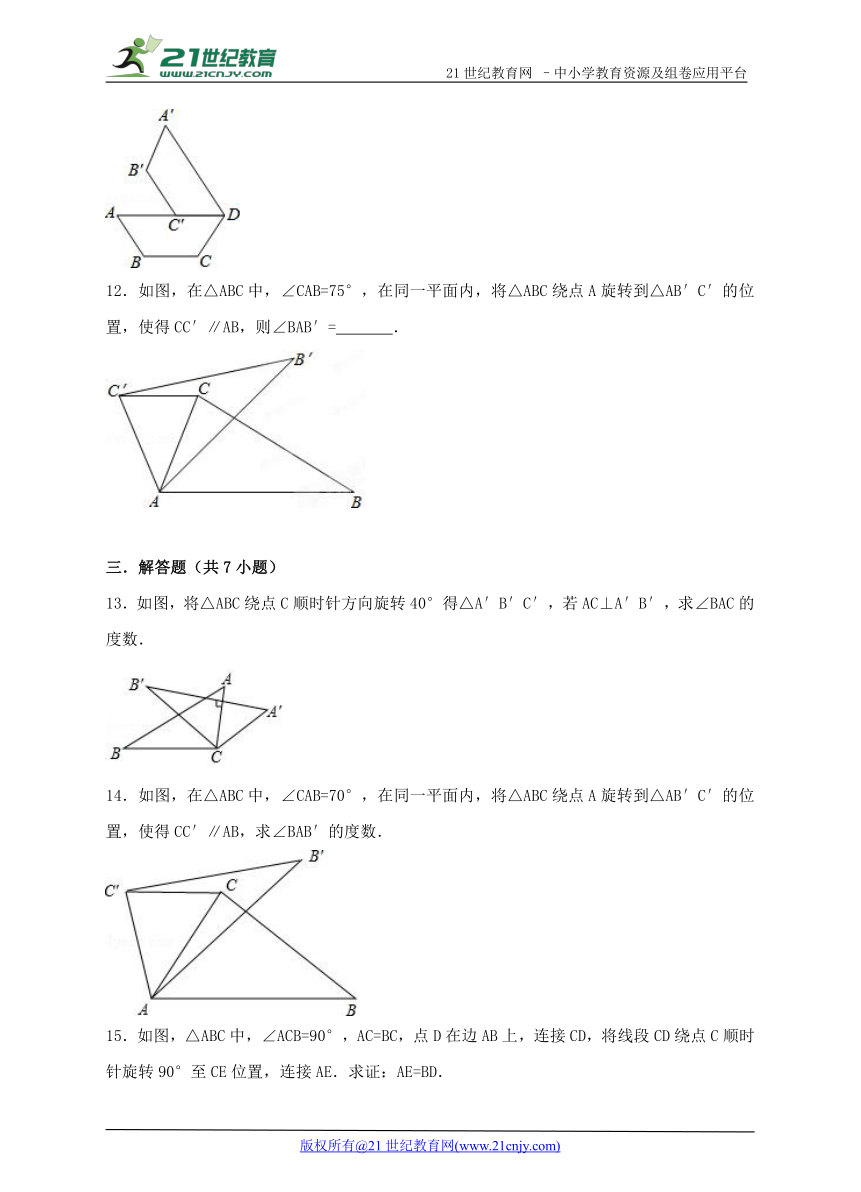
11.如图,在梯形ABCD中,AD ( http: / / www.21cnjy.com )∥BC,将这个梯形绕点D按顺时针方向旋转,使点C落在边AD上的点C′处,点B落在点B′处,如果直线B′C′经过点C,那么旋转角等于 度.
( http: / / www.21cnjy.com )
12.如图,在△ABC中,∠CAB ( http: / / www.21cnjy.com )=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′= .
( http: / / www.21cnjy.com )
三.解答题(共7小题)
13.如图,将△ABC绕点C顺时针方向旋转40°得△A′B′C′,若AC⊥A′B′,求∠BAC的度数.
( http: / / www.21cnjy.com )
14.如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,求∠BAB′的度数.
( http: / / www.21cnjy.com )
15.如图,△ABC中,∠ACB=90°,A ( http: / / www.21cnjy.com )C=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.求证:AE=BD.
( http: / / www.21cnjy.com )
16.在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.
( http: / / www.21cnjy.com )
17.已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.
(1)旋转中心是 .旋转角为 度.
(2)请你判断△DFE的形状,并说明理由.
(3)求四边形DEBF的周长和面积.
( http: / / www.21cnjy.com )
18.如图,△ACD、△A ( http: / / www.21cnjy.com )EB都是等腰直角三角形,∠CAD=∠EAB=90°,∠BAC=30°,若△EAC绕某点逆时针旋转后能与△BAD重合,问:
(1)旋转中心是 ;
(2)逆时针旋转 度;
(3)若EC=10cm,则BD的长度是 cm.
( http: / / www.21cnjy.com )
19.如图,将一个直角三角板ACB(∠C=90°)绕60°角的顶点B顺时针旋转,使得点C旋转到AB的延长线上的点E处,请解答下列问题:【版权所有:21教育】
(1)三角板旋转了多少度?
(2)连接CE,请判断△BCE的形状;
(3)求∠ACE的度数.
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共7小题)
1.
【分析】根据旋转的性质即可求出答案.
解:由题意可知:∠DOB=85°,
∵△DCO≌△BAO,
∴∠D=∠B=40°,
∴∠AOB=180°﹣40°﹣110°=30°
∴∠α=85°﹣30°=55°
故选:C.
2.
【分析】根据旋转的性质可得AB=AE,∠BAE=60°,然后判断出△AEB是等边三角形,再根据等边三角形的三条边都相等可得BE=AB.21·世纪*教育网
解:∵△ABC绕点A顺时针旋转 60°得到△AED,
∴AB=AE,∠BAE=60°,
∴△AEB是等边三角形,
∴BE=AB,
∵AB=3,
∴BE=3.
故选:B.
3.
【分析】旋转180°后, ( http: / / www.21cnjy.com )对应点与旋转中心共线,对应线段平行且相等,对应点到旋转中心的距离相等,对应角相等,其中∠ACB与∠FDE不是对应角,不能判断相等.
解:根据旋转的性质可知,
点A与点D是对应点,
BO=EO,
AB∥DE,
∠ACB=∠DFE≠∠FDE.
故选:C.
4.
【分析】由勾股定理可求得AB的长,由旋转的性质可求得AE=AC=4,则可求得BE的长.
解:
∵在△ABC中,∠C=90°,AC=4,BC=3,
∴AB=5,
又由旋转的性质可得AE=AC=4,
∴BE=AB﹣AE=5﹣4=1,
故选:A.
5.
【分析】据旋转性质得出旋转后C到D,只要根据正方形的性质和三角形的内角和定理求出∠COD即可.
解:将△CBE绕正方形的对角线交点O按逆时针方向旋转到△CDF时,C和D重合,
即∠COD是旋转角,
∵四边形ABCD是正方形,
∴∠OCD=∠ODC=45°,
∴∠COD=180°﹣45°﹣45°=90°,
即旋转角是90°,
故选:C.
( http: / / www.21cnjy.com )
6.
【分析】由三角形的外角性质得出∠BAB1=∠C+∠B=115°,即可得出结论.
解:∵C,A,B1在同一条直线上,∠C=90°,∠B=25°,
∴∠BAB1=∠C+∠B=115°.故选:D.
7.
【分析】旋转中心为点A,C、C′为对应 ( http: / / www.21cnjy.com )点,可知AC=AC′,又因为∠CAC′=90°,根据三角形外角的性质求出∠C′B′A的度数,进而求出∠B的度数.21*cnjy*com
解:由旋转的性质可知,AC=AC′,
∵∠CAC′=90°,可知△CAC′为等腰直角三角形,则∠CC′A=45°.
∵∠CC′B′=32°,
∴∠C′B′A=∠C′CA+∠CC′B′=45°+32°=77°,
∵∠B=∠C′B′A,
∴∠B=77°,
故选:C.
二.填空题(共5小题)
8.
【分析】根据旋转变化前后,对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等,即可求出答案.【来源:21·世纪·教育·网】
解:根据旋转的性质可知,∠ACB=∠A′CB′=45°,
那么旋转角度的大小为∠ACA′=180°﹣45°=135°;
故答案为:135.
9.
【分析】根据旋转角可得∠CAE=40°,然后根据∠BAE=∠BAC+∠CAE,代入数据进行计算即可得解.
解:∵△ABC绕着点A顺时针旋转40°后得到△ADE,
∴∠CAE=40°,
∵∠BAC=60°,
∴∠BAE=∠BAC+∠CAE=60°+40°=100°.
故答案为:100°.
10.
【分析】根据旋转变换只改变图形的位置不 ( http: / / www.21cnjy.com )改变图形的形状与大小可得△ABF和△ACD全等,根据全等三角形对应角相等可得∠BAF=∠CAD,然后求出∠EAF=45°.
解:∵△ADC绕A顺时针旋转90°后得到△AFB,
∴△ABF≌△ACD,
∴∠BAF=∠CAD,AF=AD,BF=CD,
∴∠EAF=∠BAF+∠BAE=∠CAD+∠BAE=∠BAC﹣∠DAE=90°﹣45°=45°,
故答案为:45°.
11.
【分析】连接CC′,则B′、C′、 ( http: / / www.21cnjy.com )C在一条直线上,由旋转的性质得出∠1=∠2,DC′=DC,得出∠3=∠4,再由平行线的性质得出∠2=∠3,证出△CDC′是等边三角形,得出∠CDC′=60°即可.www-2-1-cnjy-com
解:连接CC′,如图所示:
则B′、C′、C在一条直线上,
由旋转的性质得:∠1=∠2,DC′=DC,
∴∠3=∠4,
∵A′D′∥B′C′,
∴∠2=∠3,
∴∠1=∠3=∠4,
∴△CDC′是等边三角形,
∴∠CDC′=60°;
故答案为:60.
( http: / / www.21cnjy.com )
12.
【分析】首先证明∠ACC′=∠AC′C;然后运用三角形的内角和定理求出∠CAC′=30°即可解决问题.2·1·c·n·j·y
解:由题意得:
AC=AC′,
∴∠ACC′=∠AC′C;
∵CC′∥AB,且∠BAC=75°,
∴∠ACC′=∠AC′C=∠BAC=75°,
∴∠CAC′=180°﹣2×75°=30°;
由题意知:∠BAB′=∠CAC′=30°,
故答案为30°.
三.解答题(共7小题)
13.
【分析】根据旋转的性质可得∠ACA′=40 ,∠A=∠A′,再根据直角三角形两锐角互余列式计算即可得解.21·cn·jy·com
解:∵△ABC绕点C顺时针方向旋转40 得△A′B′C′,
∴∠ACA′=40 ,∠A=∠A′,
∵AC⊥A′B′,
∴∠A′=90°﹣40°=50°,
∴∠BAC=50°.
14.
【分析】先根据平行线的性质,由CC′∥A ( http: / / www.21cnjy.com )B得∠AC′C=∠CAB=70°,再根据旋转的性质得AC=AC′,∠BAB′=∠CAC′,于是根据等腰三角形的性质有∠ACC′=∠AC′C=70°,然后利用三角形内角和定理可计算出∠CAC′=40°,从而得到∠BAB′的度数.
解:∵CC′∥AB,
∴∠AC′C=∠CAB=70°,
∵△ABC绕点A旋转到△AB′C′的位置,
∴AC=AC′,∠BAB′=∠CAC′,
在△ACC′中,∵AC=AC′,
∴∠ACC′=∠AC′C=70°,
∴∠CAC′=180°﹣70°﹣70°=40°,
∴∠BAB′=40°.
( http: / / www.21cnjy.com )
15.
【分析】先根据旋转的性质,由线段CD ( http: / / www.21cnjy.com )绕点C顺时针旋转90°至CE位置得到CD=CE,∠DCE=90°,加上CB=CA,∠BCA=90°,于是根据旋转的定义可把△BCD绕点C顺时针旋转90°得到△ACE,然后根据旋转的性质即可得到结论.21cnjy.com
证明:∵线段CD绕点C顺时针旋转90°至CE位置,
∴CD=CE,∠DCE=90°,
∵CB=CA,∠BCA=90°,
∴△BCD绕点C顺时针旋转90°得到△ACE,
∴AE=BD.
16.
【分析】(1)先根据三角形内角和计算出∠BAC=150°,然后利用旋转的定义可判断旋转中心为点A,旋转角为150°;21世纪教育网版权所有
(2)根据旋转的性质得到∠DAE=∠BAC=150°,AB=AD=4,AC=AE,利用周角定义可得到∠BAE=60°,然后利用点C为AD中点得到AC= ( http: / / www.21cnjy.com )AD=2,于是得到AE=2.
解:(1)在△ABC中,∵∠B+∠ACB=30°,
∴∠BAC=150°,
当△ABC逆时针旋转一定角度后与△ADE重合,
∴旋转中心为点A,∠BAD等于旋转角,即旋转角为150°;
(2)∵△ABC绕点A逆时针旋转150°后与△ADE重合,
∴∠DAE=∠BAC=150°,AB=AD=4,AC=AE,
∴∠BAE=360°﹣150°﹣150°=60°,
∵点C为AD中点,
∴AC= ( http: / / www.21cnjy.com )AD=2,
∴AE=2.
17.
【分析】(1)确定旋转中心及旋转的角度,首先确定哪是对应点,即可确定旋转中心以及旋转角;
(2)根据旋转的性质,可以得到旋转前后的两个图形全等,以及旋转角的定义即可作出判断;
(3)根据△DAE≌△DCF,可以得到:AE=CF,DE=DF,则四边形DEBF的周长就是正方形的三边的和与DE的和.【来源:21cnj*y.co*m】
解:(1)旋转中心是点D.旋转角为90度.
(2)根据旋转的性质可得:△DAE≌△DCF,则DE=DF,∠EDF=∠ADC=90°,
则△DFE的形状是等腰直角三角形.
(3)四边形DEBF的周长是BE+BC+CF+DF+DE=AB+BC+DE+DF=20;
面积等于正方形ABCD的面积=16.
18.
【分析】(1)找出两重合三角形的公共顶点即可得出其旋转中心;
(2)根据两重合边所夹的角度即可求出旋转的度数;
(3)根据图形旋转的性质可直接进行解答.
解:(1)∵△EAC逆时针旋转后能与△BAD重合,
∴A点即为两三角形的公共顶点,故旋转中心是A点;
(2)∵△EAC逆时针旋转后能与△BAD,
∴AE与AB重合,
∵∠BAE=90°,
∴旋转的度数为:90;
(3)由题意知EC和BD是对应线段,据旋转的性质可得BD=EC=10cm.
故答案为:(1)A;(2)90;(3)10.
19.
【分析】(1)先利用邻补角计算出∠CBE=180°﹣∠ABC=120°,再根据旋转的性质得到∠CBE等于旋转角,所以三角板旋转了120°;www.21-cn-jy.com
(2)根据旋转的性质得BC=BE,则根据等腰三角形的判定定理即可得到△BCE为等腰三角形;
(3)由于∠CBE=120°,△BCE为等腰三角形,根据等腰三角形的性质和三角形内角和定理可计算出∠BCE= ( http: / / www.21cnjy.com )(180°﹣120°)=30°,然后利用∠ACE=∠ACB+∠BCE进行计算即可.
解:(1)∵∠ABC=60°,
∴∠CBE=180°﹣60°=120°,
∵直角三角板ACB绕顶点B顺时针旋转得到△DEB,
∴∠CBE等于旋转角,
∴三角板旋转了120°;
(2)∵直角三角板ACB绕顶点B顺时针旋转得到△DEB,
∴BC=BE,
∴△BCE为等腰三角形;
(3)∵∠CBE=120°,△BCE为等腰三角形,
∴∠BCE= ( http: / / www.21cnjy.com )(180°﹣120°)=30°,
∴∠ACE=∠ACB+∠BCE=90°+30°=120°.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
10.3.2 旋转的特征同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.旋转的特征:
①旋转后的图形上的每一点都绕 旋转中心旋转相同的角度.
②旋转前后的图形中的对应线段、对应角都相等.
③旋转前后的图形的对应点到旋转中心的距离相等 .
2.旋转前后的旋转中心的确定:任取两对对应点,画出它们的对称轴,两对称轴的交点即为旋转中心.
基础知识和能力拓展精练
一.选择题
1.如图,△OAB绕点O逆时针旋转85°得到△OCD,若∠A=110°,∠D=40°,则∠α的度数是( )21教育网
( http: / / www.21cnjy.com )
A.35° B.45° C.55° D.65°
2.如图,将△ABC绕点A顺时针旋转 60°得到△AED,若线段AB=3,则BE=( )
( http: / / www.21cnjy.com )
A.2 B.3 C.4 D.5
3.如图,△DEF是由△ABC绕点O旋转180°而得到的,则下列结论不成立的是( )
( http: / / www.21cnjy.com )
A.点A与点D是对应点 B.BO=EO C.∠ACB=∠FDE D.AB∥DE
4.如图,在△ABC中,∠C=90°,A ( http: / / www.21cnjy.com )C=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则BE的长为( )2-1-c-n-j-y
( http: / / www.21cnjy.com )
A.1 B.2 C.3 D.4
5.如图,E、F分别是正方形ABCD的边A ( http: / / www.21cnjy.com )B、BC上的点,BE=CF,连接CE、DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转角度为( )
( http: / / www.21cnjy.com )
A.45° B.60° C.90° D.120°
6.如图,将Rt△ABC(∠B=25°)绕点A顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )【出处:21教育名师】
( http: / / www.21cnjy.com )
A.65° B.80° C.105° D.115°
7.如图,在Rt△ABC中,∠BAC=90 ( http: / / www.21cnjy.com )°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( )21教育名师原创作品
( http: / / www.21cnjy.com )
A.32° B.64° C.77° D.87°
二.填空题(共5小题)
8.如图,一块等腰直角的三 ( http: / / www.21cnjy.com )角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,使A,C,B′三点共线,那么旋转角度的大小为 .21*cnjy*com
( http: / / www.21cnjy.com )
9.如图,在△ABC中,∠BAC=60°,将△ABC绕着点A顺时针旋转40°后得到△ADE,则∠BAE= .
( http: / / www.21cnjy.com )
10.如图,在Rt△ABC中,AB=A ( http: / / www.21cnjy.com )C,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连结EF.则∠EAF= .
( http: / / www.21cnjy.com )
11.如图,在梯形ABCD中,AD ( http: / / www.21cnjy.com )∥BC,将这个梯形绕点D按顺时针方向旋转,使点C落在边AD上的点C′处,点B落在点B′处,如果直线B′C′经过点C,那么旋转角等于 度.
( http: / / www.21cnjy.com )
12.如图,在△ABC中,∠CAB ( http: / / www.21cnjy.com )=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′= .
( http: / / www.21cnjy.com )
三.解答题(共7小题)
13.如图,将△ABC绕点C顺时针方向旋转40°得△A′B′C′,若AC⊥A′B′,求∠BAC的度数.
( http: / / www.21cnjy.com )
14.如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,求∠BAB′的度数.
( http: / / www.21cnjy.com )
15.如图,△ABC中,∠ACB=90°,A ( http: / / www.21cnjy.com )C=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.求证:AE=BD.
( http: / / www.21cnjy.com )
16.在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.
( http: / / www.21cnjy.com )
17.已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.
(1)旋转中心是 .旋转角为 度.
(2)请你判断△DFE的形状,并说明理由.
(3)求四边形DEBF的周长和面积.
( http: / / www.21cnjy.com )
18.如图,△ACD、△A ( http: / / www.21cnjy.com )EB都是等腰直角三角形,∠CAD=∠EAB=90°,∠BAC=30°,若△EAC绕某点逆时针旋转后能与△BAD重合,问:
(1)旋转中心是 ;
(2)逆时针旋转 度;
(3)若EC=10cm,则BD的长度是 cm.
( http: / / www.21cnjy.com )
19.如图,将一个直角三角板ACB(∠C=90°)绕60°角的顶点B顺时针旋转,使得点C旋转到AB的延长线上的点E处,请解答下列问题:【版权所有:21教育】
(1)三角板旋转了多少度?
(2)连接CE,请判断△BCE的形状;
(3)求∠ACE的度数.
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共7小题)
1.
【分析】根据旋转的性质即可求出答案.
解:由题意可知:∠DOB=85°,
∵△DCO≌△BAO,
∴∠D=∠B=40°,
∴∠AOB=180°﹣40°﹣110°=30°
∴∠α=85°﹣30°=55°
故选:C.
2.
【分析】根据旋转的性质可得AB=AE,∠BAE=60°,然后判断出△AEB是等边三角形,再根据等边三角形的三条边都相等可得BE=AB.21·世纪*教育网
解:∵△ABC绕点A顺时针旋转 60°得到△AED,
∴AB=AE,∠BAE=60°,
∴△AEB是等边三角形,
∴BE=AB,
∵AB=3,
∴BE=3.
故选:B.
3.
【分析】旋转180°后, ( http: / / www.21cnjy.com )对应点与旋转中心共线,对应线段平行且相等,对应点到旋转中心的距离相等,对应角相等,其中∠ACB与∠FDE不是对应角,不能判断相等.
解:根据旋转的性质可知,
点A与点D是对应点,
BO=EO,
AB∥DE,
∠ACB=∠DFE≠∠FDE.
故选:C.
4.
【分析】由勾股定理可求得AB的长,由旋转的性质可求得AE=AC=4,则可求得BE的长.
解:
∵在△ABC中,∠C=90°,AC=4,BC=3,
∴AB=5,
又由旋转的性质可得AE=AC=4,
∴BE=AB﹣AE=5﹣4=1,
故选:A.
5.
【分析】据旋转性质得出旋转后C到D,只要根据正方形的性质和三角形的内角和定理求出∠COD即可.
解:将△CBE绕正方形的对角线交点O按逆时针方向旋转到△CDF时,C和D重合,
即∠COD是旋转角,
∵四边形ABCD是正方形,
∴∠OCD=∠ODC=45°,
∴∠COD=180°﹣45°﹣45°=90°,
即旋转角是90°,
故选:C.
( http: / / www.21cnjy.com )
6.
【分析】由三角形的外角性质得出∠BAB1=∠C+∠B=115°,即可得出结论.
解:∵C,A,B1在同一条直线上,∠C=90°,∠B=25°,
∴∠BAB1=∠C+∠B=115°.故选:D.
7.
【分析】旋转中心为点A,C、C′为对应 ( http: / / www.21cnjy.com )点,可知AC=AC′,又因为∠CAC′=90°,根据三角形外角的性质求出∠C′B′A的度数,进而求出∠B的度数.21*cnjy*com
解:由旋转的性质可知,AC=AC′,
∵∠CAC′=90°,可知△CAC′为等腰直角三角形,则∠CC′A=45°.
∵∠CC′B′=32°,
∴∠C′B′A=∠C′CA+∠CC′B′=45°+32°=77°,
∵∠B=∠C′B′A,
∴∠B=77°,
故选:C.
二.填空题(共5小题)
8.
【分析】根据旋转变化前后,对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等,即可求出答案.【来源:21·世纪·教育·网】
解:根据旋转的性质可知,∠ACB=∠A′CB′=45°,
那么旋转角度的大小为∠ACA′=180°﹣45°=135°;
故答案为:135.
9.
【分析】根据旋转角可得∠CAE=40°,然后根据∠BAE=∠BAC+∠CAE,代入数据进行计算即可得解.
解:∵△ABC绕着点A顺时针旋转40°后得到△ADE,
∴∠CAE=40°,
∵∠BAC=60°,
∴∠BAE=∠BAC+∠CAE=60°+40°=100°.
故答案为:100°.
10.
【分析】根据旋转变换只改变图形的位置不 ( http: / / www.21cnjy.com )改变图形的形状与大小可得△ABF和△ACD全等,根据全等三角形对应角相等可得∠BAF=∠CAD,然后求出∠EAF=45°.
解:∵△ADC绕A顺时针旋转90°后得到△AFB,
∴△ABF≌△ACD,
∴∠BAF=∠CAD,AF=AD,BF=CD,
∴∠EAF=∠BAF+∠BAE=∠CAD+∠BAE=∠BAC﹣∠DAE=90°﹣45°=45°,
故答案为:45°.
11.
【分析】连接CC′,则B′、C′、 ( http: / / www.21cnjy.com )C在一条直线上,由旋转的性质得出∠1=∠2,DC′=DC,得出∠3=∠4,再由平行线的性质得出∠2=∠3,证出△CDC′是等边三角形,得出∠CDC′=60°即可.www-2-1-cnjy-com
解:连接CC′,如图所示:
则B′、C′、C在一条直线上,
由旋转的性质得:∠1=∠2,DC′=DC,
∴∠3=∠4,
∵A′D′∥B′C′,
∴∠2=∠3,
∴∠1=∠3=∠4,
∴△CDC′是等边三角形,
∴∠CDC′=60°;
故答案为:60.
( http: / / www.21cnjy.com )
12.
【分析】首先证明∠ACC′=∠AC′C;然后运用三角形的内角和定理求出∠CAC′=30°即可解决问题.2·1·c·n·j·y
解:由题意得:
AC=AC′,
∴∠ACC′=∠AC′C;
∵CC′∥AB,且∠BAC=75°,
∴∠ACC′=∠AC′C=∠BAC=75°,
∴∠CAC′=180°﹣2×75°=30°;
由题意知:∠BAB′=∠CAC′=30°,
故答案为30°.
三.解答题(共7小题)
13.
【分析】根据旋转的性质可得∠ACA′=40 ,∠A=∠A′,再根据直角三角形两锐角互余列式计算即可得解.21·cn·jy·com
解:∵△ABC绕点C顺时针方向旋转40 得△A′B′C′,
∴∠ACA′=40 ,∠A=∠A′,
∵AC⊥A′B′,
∴∠A′=90°﹣40°=50°,
∴∠BAC=50°.
14.
【分析】先根据平行线的性质,由CC′∥A ( http: / / www.21cnjy.com )B得∠AC′C=∠CAB=70°,再根据旋转的性质得AC=AC′,∠BAB′=∠CAC′,于是根据等腰三角形的性质有∠ACC′=∠AC′C=70°,然后利用三角形内角和定理可计算出∠CAC′=40°,从而得到∠BAB′的度数.
解:∵CC′∥AB,
∴∠AC′C=∠CAB=70°,
∵△ABC绕点A旋转到△AB′C′的位置,
∴AC=AC′,∠BAB′=∠CAC′,
在△ACC′中,∵AC=AC′,
∴∠ACC′=∠AC′C=70°,
∴∠CAC′=180°﹣70°﹣70°=40°,
∴∠BAB′=40°.
( http: / / www.21cnjy.com )
15.
【分析】先根据旋转的性质,由线段CD ( http: / / www.21cnjy.com )绕点C顺时针旋转90°至CE位置得到CD=CE,∠DCE=90°,加上CB=CA,∠BCA=90°,于是根据旋转的定义可把△BCD绕点C顺时针旋转90°得到△ACE,然后根据旋转的性质即可得到结论.21cnjy.com
证明:∵线段CD绕点C顺时针旋转90°至CE位置,
∴CD=CE,∠DCE=90°,
∵CB=CA,∠BCA=90°,
∴△BCD绕点C顺时针旋转90°得到△ACE,
∴AE=BD.
16.
【分析】(1)先根据三角形内角和计算出∠BAC=150°,然后利用旋转的定义可判断旋转中心为点A,旋转角为150°;21世纪教育网版权所有
(2)根据旋转的性质得到∠DAE=∠BAC=150°,AB=AD=4,AC=AE,利用周角定义可得到∠BAE=60°,然后利用点C为AD中点得到AC= ( http: / / www.21cnjy.com )AD=2,于是得到AE=2.
解:(1)在△ABC中,∵∠B+∠ACB=30°,
∴∠BAC=150°,
当△ABC逆时针旋转一定角度后与△ADE重合,
∴旋转中心为点A,∠BAD等于旋转角,即旋转角为150°;
(2)∵△ABC绕点A逆时针旋转150°后与△ADE重合,
∴∠DAE=∠BAC=150°,AB=AD=4,AC=AE,
∴∠BAE=360°﹣150°﹣150°=60°,
∵点C为AD中点,
∴AC= ( http: / / www.21cnjy.com )AD=2,
∴AE=2.
17.
【分析】(1)确定旋转中心及旋转的角度,首先确定哪是对应点,即可确定旋转中心以及旋转角;
(2)根据旋转的性质,可以得到旋转前后的两个图形全等,以及旋转角的定义即可作出判断;
(3)根据△DAE≌△DCF,可以得到:AE=CF,DE=DF,则四边形DEBF的周长就是正方形的三边的和与DE的和.【来源:21cnj*y.co*m】
解:(1)旋转中心是点D.旋转角为90度.
(2)根据旋转的性质可得:△DAE≌△DCF,则DE=DF,∠EDF=∠ADC=90°,
则△DFE的形状是等腰直角三角形.
(3)四边形DEBF的周长是BE+BC+CF+DF+DE=AB+BC+DE+DF=20;
面积等于正方形ABCD的面积=16.
18.
【分析】(1)找出两重合三角形的公共顶点即可得出其旋转中心;
(2)根据两重合边所夹的角度即可求出旋转的度数;
(3)根据图形旋转的性质可直接进行解答.
解:(1)∵△EAC逆时针旋转后能与△BAD重合,
∴A点即为两三角形的公共顶点,故旋转中心是A点;
(2)∵△EAC逆时针旋转后能与△BAD,
∴AE与AB重合,
∵∠BAE=90°,
∴旋转的度数为:90;
(3)由题意知EC和BD是对应线段,据旋转的性质可得BD=EC=10cm.
故答案为:(1)A;(2)90;(3)10.
19.
【分析】(1)先利用邻补角计算出∠CBE=180°﹣∠ABC=120°,再根据旋转的性质得到∠CBE等于旋转角,所以三角板旋转了120°;www.21-cn-jy.com
(2)根据旋转的性质得BC=BE,则根据等腰三角形的判定定理即可得到△BCE为等腰三角形;
(3)由于∠CBE=120°,△BCE为等腰三角形,根据等腰三角形的性质和三角形内角和定理可计算出∠BCE= ( http: / / www.21cnjy.com )(180°﹣120°)=30°,然后利用∠ACE=∠ACB+∠BCE进行计算即可.
解:(1)∵∠ABC=60°,
∴∠CBE=180°﹣60°=120°,
∵直角三角板ACB绕顶点B顺时针旋转得到△DEB,
∴∠CBE等于旋转角,
∴三角板旋转了120°;
(2)∵直角三角板ACB绕顶点B顺时针旋转得到△DEB,
∴BC=BE,
∴△BCE为等腰三角形;
(3)∵∠CBE=120°,△BCE为等腰三角形,
∴∠BCE= ( http: / / www.21cnjy.com )(180°﹣120°)=30°,
∴∠ACE=∠ACB+∠BCE=90°+30°=120°.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
