10.4 中心对称同步练习
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
10.4 中心对称同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.把一个图形绕着某一点旋转 180°,如果旋转后的图形与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做对称中心 . 21世纪教育网版权所有
2.把一个图形绕着某一点旋转 180° ( http: / / www.21cnjy.com ),如果它能够与另一个图形重合,那么我们就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
3.在成中心对称的两个图形中,连结对称点的 ( http: / / www.21cnjy.com )线段都经过 对称中心,并且被对称中心平分 ,反过来,如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.21·cn·jy·com
基础知识和能力拓展精练
一.选择题(共7小题)
1.下面四个手机应用图标中,属于中心对称图形的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
2.已知四边形ABCD与四边形A′B′C′D′关于点O成中心对称,则AB与A′B′的关系是( )
A.相等 B.垂直
C.相等并且平行 D.相等并且平行或相等并且在同一直线上
3.如图,△ABC与△A1B1C1关于点O成中心对称,下列说法:①∠BAC=∠B1A1C1;②AC=A1C1;③OA=OA1;④△ABC与△A1B1C1的面积相等,其中正确的有( )
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
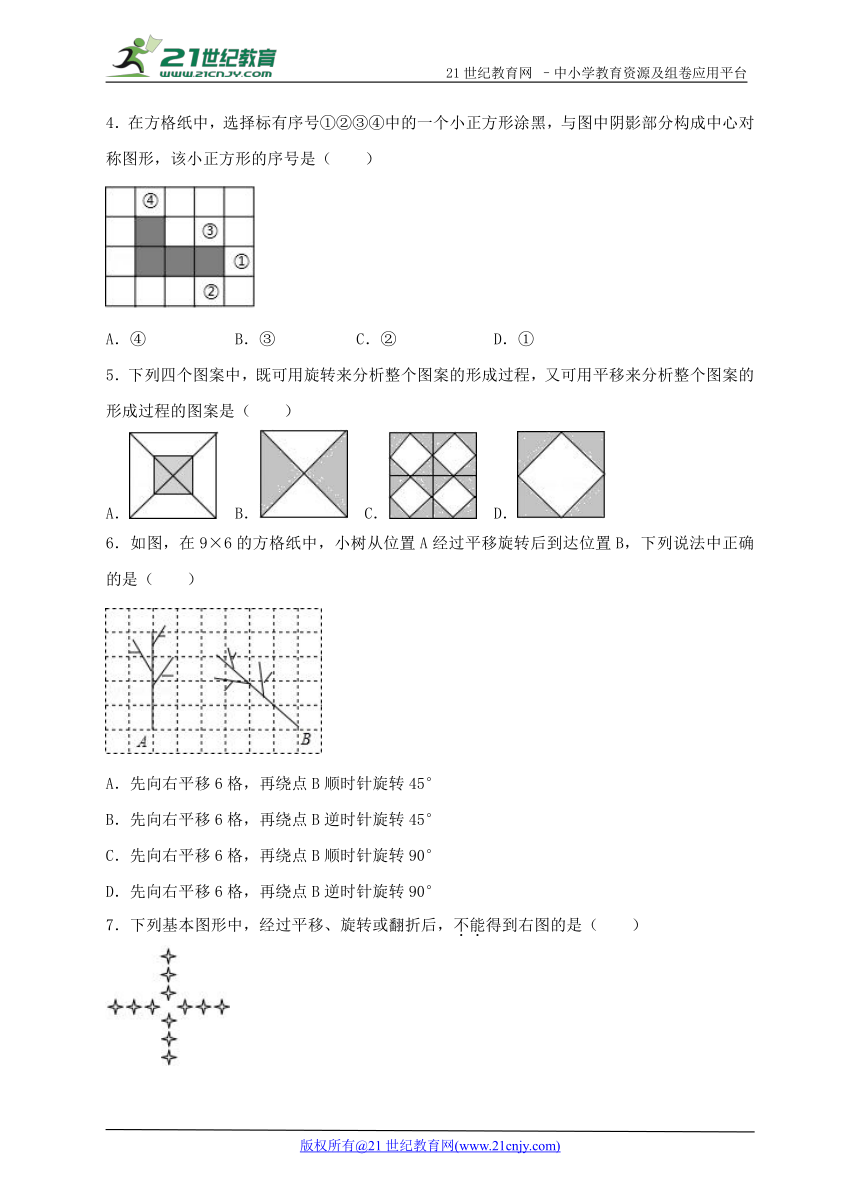
4.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,该小正方形的序号是( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
A.④ B.③ C.② D.①
5.下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的图案是( )2-1-c-n-j-y
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
6.如图,在9×6的方格纸中,小树从位置A经过平移旋转后到达位置B,下列说法中正确的是( )
( http: / / www.21cnjy.com )
A.先向右平移6格,再绕点B顺时针旋转45°
B.先向右平移6格,再绕点B逆时针旋转45°
C.先向右平移6格,再绕点B顺时针旋转90°
D.先向右平移6格,再绕点B逆时针旋转90°
7.下列基本图形中,经过平移、旋转或翻折后,不能得到右图的是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二.填空题(共5小题)
8.平行四边形是 对称图形.(“轴对称图形”或“中心对称图形”)
9.下列图形中:①圆;②等腰三角形;③正方形;④正五边形,既是轴对称图形又是中心对称图形的有 个.21·世纪*教育网
10.如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转 次,每次旋转 度形成的.【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
11.如图是3×4正方形网格,其中已有5各 ( http: / / www.21cnjy.com )小方格涂上阴影,若再选取标有①,②,③,④中的一个小方格涂上阴影,使图中所有涂上阴影的小方格组成一个中心对称图形,则该小方格是 .(填序号)【出处:21教育名师】
( http: / / www.21cnjy.com )
12.如图,图①经过 ( http: / / www.21cnjy.com ) 变换得到图②;图①经过 变换得到图③;图①经过 变换得到图④.(填“平移”、“旋转”或“轴对称”)【版权所有:21教育】
( http: / / www.21cnjy.com )
三.解答题(共7小题)
13.如图,已知△ABC与△A′B′C′成中心对称图形,求出它的对称中心O.
( http: / / www.21cnjy.com )
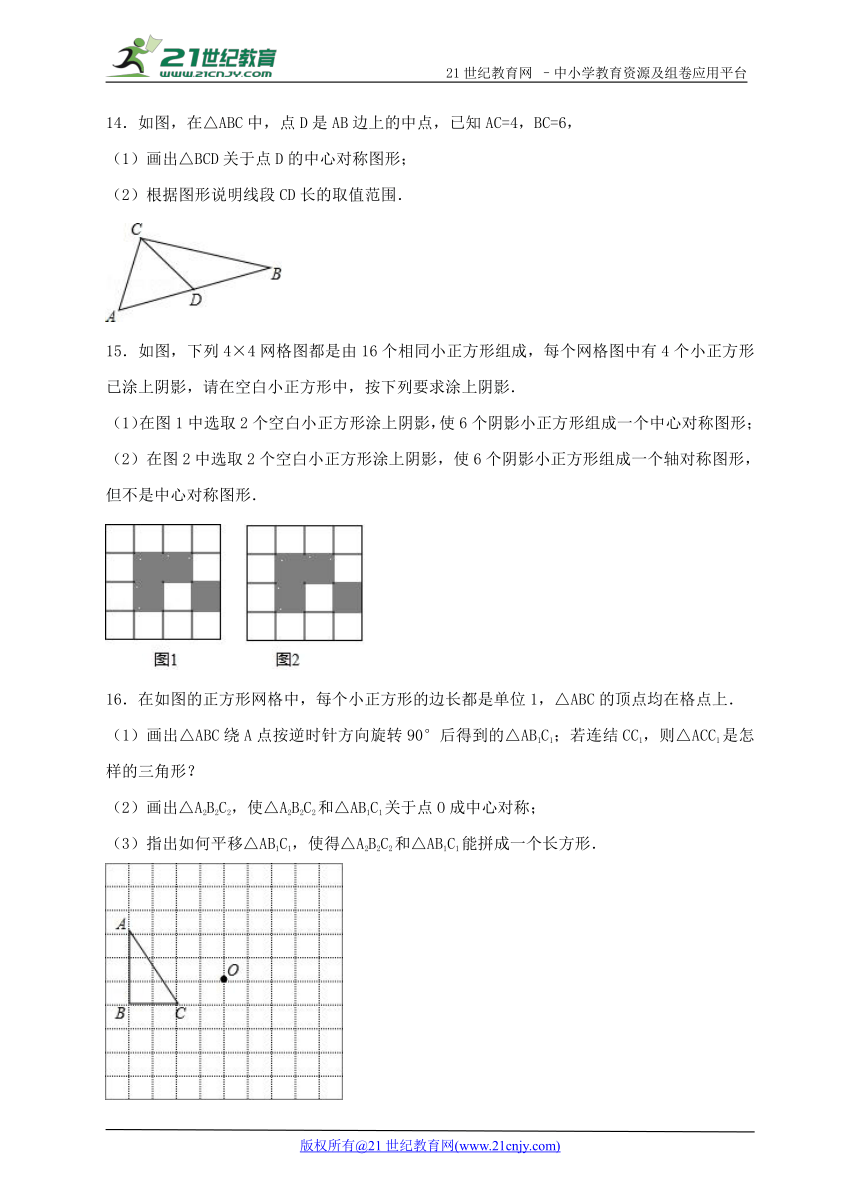
14.如图,在△ABC中,点D是AB边上的中点,已知AC=4,BC=6,
(1)画出△BCD关于点D的中心对称图形;
(2)根据图形说明线段CD长的取值范围.
( http: / / www.21cnjy.com )
15.如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.21教育名师原创作品
(1)在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.21*cnjy*com
( http: / / www.21cnjy.com )
16.在如图的正方形网格中,每个小正方形的边长都是单位1,△ABC的顶点均在格点上.
(1)画出△ABC绕A点按逆时针方向旋转90°后得到的△AB1C1;若连结CC1,则△ACC1是怎样的三角形?
(2)画出△A2B2C2,使△A2B2C2和△AB1C1关于点O成中心对称;
(3)指出如何平移△AB1C1,使得△A2B2C2和△AB1C1能拼成一个长方形.
( http: / / www.21cnjy.com )
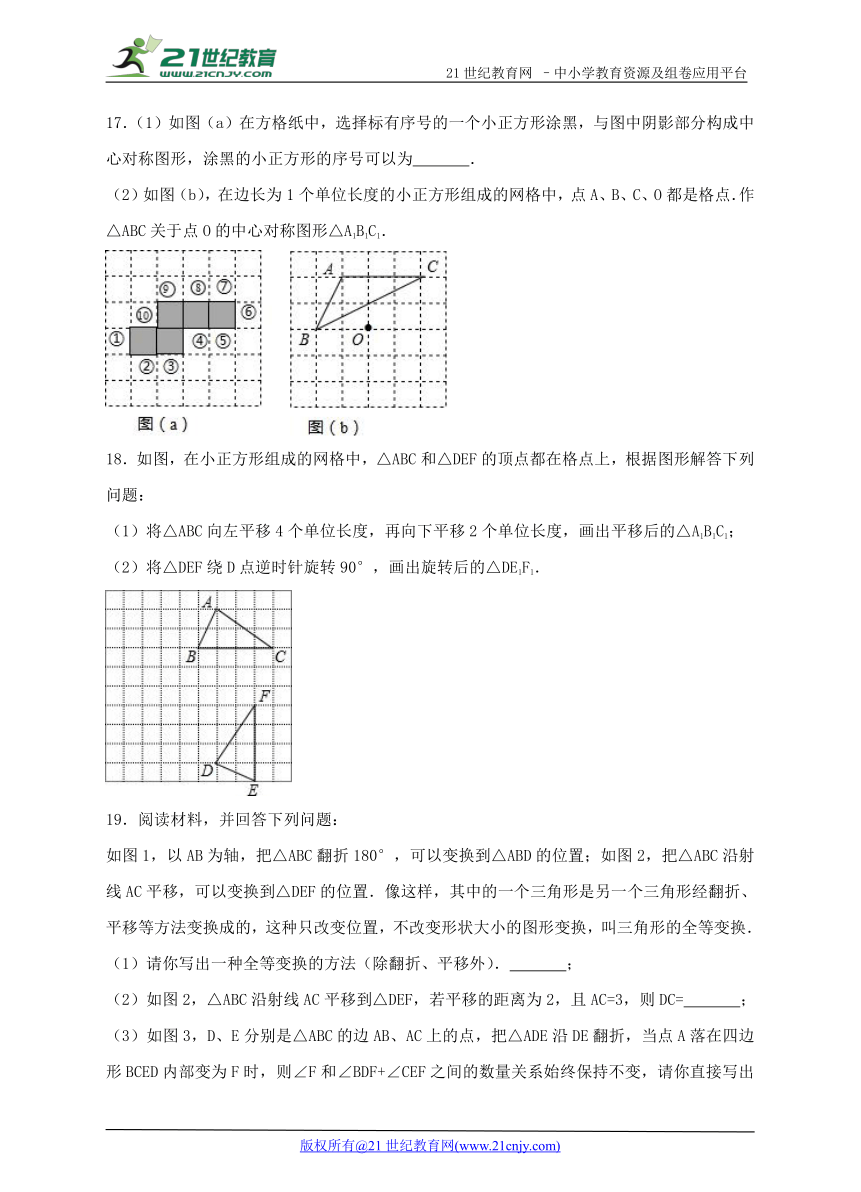
17.(1)如图(a)在方格纸中,选择标有序号的一个小正方形涂黑,与图中阴影部分构成中心对称图形,涂黑的小正方形的序号可以为 .
(2)如图(b),在边长为1个单位长度的小正方形组成的网格中,点A、B、C、O都是格点.作△ABC关于点O的中心对称图形△A1B1C1.
( http: / / www.21cnjy.com )
18.如图,在小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,根据图形解答下列问题:
(1)将△ABC向左平移4个单位长度,再向下平移2个单位长度,画出平移后的△A1B1C1;
(2)将△DEF绕D点逆时针旋转90°,画出旋转后的△DE1F1.
( http: / / www.21cnjy.com )
19.阅读材料,并回答下列问题:
如图1,以AB为轴,把△ABC翻折18 ( http: / / www.21cnjy.com )0°,可以变换到△ABD的位置;如图2,把△ABC沿射线AC平移,可以变换到△DEF的位置.像这样,其中的一个三角形是另一个三角形经翻折、平移等方法变换成的,这种只改变位置,不改变形状大小的图形变换,叫三角形的全等变换.
(1)请你写出一种全等变换的方法(除翻折、平移外). ;
(2)如图2,△ABC沿射线AC平移到△DEF,若平移的距离为2,且AC=3,则DC= ;
(3)如图3,D、E分别是△ABC ( http: / / www.21cnjy.com )的边AB、AC上的点,把△ADE沿DE翻折,当点A落在四边形BCED内部变为F时,则∠F和∠BDF+∠CEF之间的数量关系始终保持不变,请你直接写出它们之间的关系式: .2·1·c·n·j·y
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共7小题)
1.
【分析】根据中心对称图形的概念进行判断即可.
解:A图形不是中心对称图形;
B图形是中心对称图形;
C图形不是中心对称图形;
D图形不是中心对称图形,
故选:B.
2.
【分析】根据中心对称的性质即可得到结论.
解:∵四边形ABCD与四边形A′B′C′D′关于点O成中心对称,
∴AB与A′B′的关系是相等并且平行或相等并且在同一直线上,
故选:D.
3.
【分析】根据中心对称的图形的性质即可判断.
解:中心对称的两个图形全等,则①②④正确;
对称点到对称中心的距离相等,故③正确;
故①②③④都正确.
故选:D.
4.
【分析】根据中心对称图形的特点进行判断即可.
解:应该将②涂黑.
故选:C.
5.
【分析】分别根据旋转的定义及平移的定义逐项分析即可.
解:
A、B、C、D四个选项中的图形都可以看成是图形的一半旋转180°得到,
若一个图形可以通过某一个基本图形平移得到,则这个图形可以分成几个相同的基本图形,且基本图形之间对应点的连线应该是平行的,21教育网
故A、B、D不能由平移得到,只有C选项的图形,可看成是由基本图形 ( http: / / www.21cnjy.com )通过平移得到,
故选:C.
6.
【分析】先判断出∠1的度数,再进行解答即可.
解:∵小树经过正方形BCDE的顶点B、D, ( http: / / www.21cnjy.com )
∴∠1=45°,
∴小树从位置A经过旋转平移后到位置B时应绕B点逆时针旋转45°,再向右平移6格.
故选:B.
7.
【分析】利用平移和旋转对A进行判断;利用旋转对B进行判断;利用翻折对D进行判断.
解:A、把 ( http: / / www.21cnjy.com )平移得到 ( http: / / www.21cnjy.com ),然后把 ( http: / / www.21cnjy.com )旋转可得到右图;
B、把 ( http: / / www.21cnjy.com )旋转可得到右图;
C、把 ( http: / / www.21cnjy.com )经过平移、旋转或翻折后,都不能得到右图;
D、把 ( http: / / www.21cnjy.com )翻折后可得到右图.
故选:C.
二.填空题(共5小题)
8.
【分析】根据平行四边形的对称性解答.
解:平行四边形是中心对称图形.
故答案为:中心.
9.
【分析】根据轴对称图形与中心对称图形的概念求解.
解:①既是轴对称图形又是中心对称图形,符合题意;
②是轴对称图形,不是中心对称图形,不符合题意;
③既是轴对称图形又是中心对称图形,符合题意;
④是轴对称图形,不是中心对称图形,不符合题意;
故既是轴对称图形又是中心对称图形的是①③共2个.
故答案为:2.
10.
【分析】利用旋转中的三个要素(①旋转中心; ②旋转方向; ③旋转角度)设计图案,进而判断出基本图形和旋转次数与角度.21cnjy.com
解:如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转7次,每次旋转45度形成的,
故答案为:7;45.
11.
【分析】把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,据此判断即可.www-2-1-cnjy-com
解:若标有①的一个小方格涂上阴影,则图中所有涂上阴影的小方格组成的图形不是中心对称图形;
若标有②的一个小方格涂上阴影,则图中所有涂上阴影的小方格组成一个轴对称图形;
若标有③的一个小方格涂上阴影,则图中所有涂上阴影的小方格组成一个轴对称图形;
若标有④的一个小方格涂上阴影,则图中所有涂上阴影的小方格组成一个中心对称图形;
故答案为:④.
12.
【分析】根据旋转和平移的定义,直接求解.
解:图①经过轴对称变换得到图②;图①经过旋转变换得到图③;图①经过平移变换得到图④.
故答案为:轴对称;旋转;平移.
三.解答题(共7小题)
13.
【分析】连接对应点BB′、CC′,根据对应点的连线经过对称中心,则交点就是对称中心O点.
解:连接BB′,找BB′中点O或者连接BB′、CC′,交点为对称中心O.
如图所示:
( http: / / www.21cnjy.com )
14.
【分析】(1)根据中心对称图形的性质找出各顶点的对应点,然后顺次连接即可;
(2)根据三角形的三边关系求解即可.
解:(1)所画图形如下所示:
( http: / / www.21cnjy.com )
△ADE就是所作的图形.
(2)由(1)知:△ADE≌△BDC,
则CD=DE,AE=BC,
∴AE﹣AC<2CD<AE+AC,即BC﹣AC<2CD<BC+AC,
∴2<2CD<10,
解得:1<CD<5.
15.
【分析】(1)根据中心对称图形,画出所有可能的图形即可.
(2)根据是轴对称图形,不是中心对称图形,画出图形即可.
解:(1)在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形,答案如图所示;21*cnjy*com
( http: / / www.21cnjy.com )
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形,答案如图所示;www.21-cn-jy.com
( http: / / www.21cnjy.com )
16.
【分析】(1)利用旋转的性质得出,△ACC1的形状即可;
(2)利用关于点O成中心对称的性质得出对应点坐标即可;
(3)利用平移的性质得出平移方法即可.
解:(1)如图,∵AC=AC1,∠CAC1=90°,
∴△ACC1是等腰直角三角形;
(2)如图,△A2B2C2,即为所求;
(3)答案不唯一.如:
①先将△AB1C1向右平移5个单位,然后再向下平移6个单位.
②先将△AB1C1向下平移6个单位,然后再向右平移5个单位.
③将△AB1C1沿着点C1到点A2的方向,平移的距离为C1 A2的长度单位.
( http: / / www.21cnjy.com )
17.
【分析】(1)直接利用中心对称图形的定义分析得出答案;
(2)直接利用中心对称图形的定义得出对应点位置进而得出答案.
解:(1)如图a所示:图中阴影部分构成中心对称图形是①④,
故答案为:①④;
(2)如图b,△A1B1C1,即为所求.
( http: / / www.21cnjy.com )
18.
【分析】(1)根据图形平移的性质画出平移后的△A1B1C1即可;
(2)根据图形旋转的性质画出旋转后的△DE1F1即可.
解(1)如图所示:△A1B1C1即为所求;
(2)如图所示:△DE1F1即为所求;
( http: / / www.21cnjy.com )
19.
【分析】(1)根据三种全等变换翻折、平移、旋转的定义可知判断;
(2)根据平移的距离的定义可知AD=2,则DC=AC﹣AD;
(3)根据轴对称及三角形内角和定理得出.
解:(1)旋转;
(2)∵AD=2,
∴DC=AC﹣AD=3﹣2=1;
(3)∵把△ADE沿DE翻折,得到△FDE,
∴∠ADE=∠FDE,∠AED=∠FED,
在△DEF中,∠F=180°﹣(∠FDE+∠FED);
由平角定义知,∠BDF=180°﹣∠FDA=180°﹣2∠FDE,
∠CEF=180°﹣∠FEA=180°﹣2∠FED,
∴∠BDF+∠CEF=180°﹣2∠FDE+180°﹣2∠FED=2[180°﹣(∠FDE+∠FED)]
∴∠BDF+∠CEF=2∠F.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
10.4 中心对称同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.把一个图形绕着某一点旋转 180°,如果旋转后的图形与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做对称中心 . 21世纪教育网版权所有
2.把一个图形绕着某一点旋转 180° ( http: / / www.21cnjy.com ),如果它能够与另一个图形重合,那么我们就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
3.在成中心对称的两个图形中,连结对称点的 ( http: / / www.21cnjy.com )线段都经过 对称中心,并且被对称中心平分 ,反过来,如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.21·cn·jy·com
基础知识和能力拓展精练
一.选择题(共7小题)
1.下面四个手机应用图标中,属于中心对称图形的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
2.已知四边形ABCD与四边形A′B′C′D′关于点O成中心对称,则AB与A′B′的关系是( )
A.相等 B.垂直
C.相等并且平行 D.相等并且平行或相等并且在同一直线上
3.如图,△ABC与△A1B1C1关于点O成中心对称,下列说法:①∠BAC=∠B1A1C1;②AC=A1C1;③OA=OA1;④△ABC与△A1B1C1的面积相等,其中正确的有( )
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
4.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,该小正方形的序号是( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
A.④ B.③ C.② D.①
5.下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的图案是( )2-1-c-n-j-y
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
6.如图,在9×6的方格纸中,小树从位置A经过平移旋转后到达位置B,下列说法中正确的是( )
( http: / / www.21cnjy.com )
A.先向右平移6格,再绕点B顺时针旋转45°
B.先向右平移6格,再绕点B逆时针旋转45°
C.先向右平移6格,再绕点B顺时针旋转90°
D.先向右平移6格,再绕点B逆时针旋转90°
7.下列基本图形中,经过平移、旋转或翻折后,不能得到右图的是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二.填空题(共5小题)
8.平行四边形是 对称图形.(“轴对称图形”或“中心对称图形”)
9.下列图形中:①圆;②等腰三角形;③正方形;④正五边形,既是轴对称图形又是中心对称图形的有 个.21·世纪*教育网
10.如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转 次,每次旋转 度形成的.【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
11.如图是3×4正方形网格,其中已有5各 ( http: / / www.21cnjy.com )小方格涂上阴影,若再选取标有①,②,③,④中的一个小方格涂上阴影,使图中所有涂上阴影的小方格组成一个中心对称图形,则该小方格是 .(填序号)【出处:21教育名师】
( http: / / www.21cnjy.com )
12.如图,图①经过 ( http: / / www.21cnjy.com ) 变换得到图②;图①经过 变换得到图③;图①经过 变换得到图④.(填“平移”、“旋转”或“轴对称”)【版权所有:21教育】
( http: / / www.21cnjy.com )
三.解答题(共7小题)
13.如图,已知△ABC与△A′B′C′成中心对称图形,求出它的对称中心O.
( http: / / www.21cnjy.com )
14.如图,在△ABC中,点D是AB边上的中点,已知AC=4,BC=6,
(1)画出△BCD关于点D的中心对称图形;
(2)根据图形说明线段CD长的取值范围.
( http: / / www.21cnjy.com )
15.如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.21教育名师原创作品
(1)在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.21*cnjy*com
( http: / / www.21cnjy.com )
16.在如图的正方形网格中,每个小正方形的边长都是单位1,△ABC的顶点均在格点上.
(1)画出△ABC绕A点按逆时针方向旋转90°后得到的△AB1C1;若连结CC1,则△ACC1是怎样的三角形?
(2)画出△A2B2C2,使△A2B2C2和△AB1C1关于点O成中心对称;
(3)指出如何平移△AB1C1,使得△A2B2C2和△AB1C1能拼成一个长方形.
( http: / / www.21cnjy.com )
17.(1)如图(a)在方格纸中,选择标有序号的一个小正方形涂黑,与图中阴影部分构成中心对称图形,涂黑的小正方形的序号可以为 .
(2)如图(b),在边长为1个单位长度的小正方形组成的网格中,点A、B、C、O都是格点.作△ABC关于点O的中心对称图形△A1B1C1.
( http: / / www.21cnjy.com )
18.如图,在小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,根据图形解答下列问题:
(1)将△ABC向左平移4个单位长度,再向下平移2个单位长度,画出平移后的△A1B1C1;
(2)将△DEF绕D点逆时针旋转90°,画出旋转后的△DE1F1.
( http: / / www.21cnjy.com )
19.阅读材料,并回答下列问题:
如图1,以AB为轴,把△ABC翻折18 ( http: / / www.21cnjy.com )0°,可以变换到△ABD的位置;如图2,把△ABC沿射线AC平移,可以变换到△DEF的位置.像这样,其中的一个三角形是另一个三角形经翻折、平移等方法变换成的,这种只改变位置,不改变形状大小的图形变换,叫三角形的全等变换.
(1)请你写出一种全等变换的方法(除翻折、平移外). ;
(2)如图2,△ABC沿射线AC平移到△DEF,若平移的距离为2,且AC=3,则DC= ;
(3)如图3,D、E分别是△ABC ( http: / / www.21cnjy.com )的边AB、AC上的点,把△ADE沿DE翻折,当点A落在四边形BCED内部变为F时,则∠F和∠BDF+∠CEF之间的数量关系始终保持不变,请你直接写出它们之间的关系式: .2·1·c·n·j·y
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共7小题)
1.
【分析】根据中心对称图形的概念进行判断即可.
解:A图形不是中心对称图形;
B图形是中心对称图形;
C图形不是中心对称图形;
D图形不是中心对称图形,
故选:B.
2.
【分析】根据中心对称的性质即可得到结论.
解:∵四边形ABCD与四边形A′B′C′D′关于点O成中心对称,
∴AB与A′B′的关系是相等并且平行或相等并且在同一直线上,
故选:D.
3.
【分析】根据中心对称的图形的性质即可判断.
解:中心对称的两个图形全等,则①②④正确;
对称点到对称中心的距离相等,故③正确;
故①②③④都正确.
故选:D.
4.
【分析】根据中心对称图形的特点进行判断即可.
解:应该将②涂黑.
故选:C.
5.
【分析】分别根据旋转的定义及平移的定义逐项分析即可.
解:
A、B、C、D四个选项中的图形都可以看成是图形的一半旋转180°得到,
若一个图形可以通过某一个基本图形平移得到,则这个图形可以分成几个相同的基本图形,且基本图形之间对应点的连线应该是平行的,21教育网
故A、B、D不能由平移得到,只有C选项的图形,可看成是由基本图形 ( http: / / www.21cnjy.com )通过平移得到,
故选:C.
6.
【分析】先判断出∠1的度数,再进行解答即可.
解:∵小树经过正方形BCDE的顶点B、D, ( http: / / www.21cnjy.com )
∴∠1=45°,
∴小树从位置A经过旋转平移后到位置B时应绕B点逆时针旋转45°,再向右平移6格.
故选:B.
7.
【分析】利用平移和旋转对A进行判断;利用旋转对B进行判断;利用翻折对D进行判断.
解:A、把 ( http: / / www.21cnjy.com )平移得到 ( http: / / www.21cnjy.com ),然后把 ( http: / / www.21cnjy.com )旋转可得到右图;
B、把 ( http: / / www.21cnjy.com )旋转可得到右图;
C、把 ( http: / / www.21cnjy.com )经过平移、旋转或翻折后,都不能得到右图;
D、把 ( http: / / www.21cnjy.com )翻折后可得到右图.
故选:C.
二.填空题(共5小题)
8.
【分析】根据平行四边形的对称性解答.
解:平行四边形是中心对称图形.
故答案为:中心.
9.
【分析】根据轴对称图形与中心对称图形的概念求解.
解:①既是轴对称图形又是中心对称图形,符合题意;
②是轴对称图形,不是中心对称图形,不符合题意;
③既是轴对称图形又是中心对称图形,符合题意;
④是轴对称图形,不是中心对称图形,不符合题意;
故既是轴对称图形又是中心对称图形的是①③共2个.
故答案为:2.
10.
【分析】利用旋转中的三个要素(①旋转中心; ②旋转方向; ③旋转角度)设计图案,进而判断出基本图形和旋转次数与角度.21cnjy.com
解:如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转7次,每次旋转45度形成的,
故答案为:7;45.
11.
【分析】把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,据此判断即可.www-2-1-cnjy-com
解:若标有①的一个小方格涂上阴影,则图中所有涂上阴影的小方格组成的图形不是中心对称图形;
若标有②的一个小方格涂上阴影,则图中所有涂上阴影的小方格组成一个轴对称图形;
若标有③的一个小方格涂上阴影,则图中所有涂上阴影的小方格组成一个轴对称图形;
若标有④的一个小方格涂上阴影,则图中所有涂上阴影的小方格组成一个中心对称图形;
故答案为:④.
12.
【分析】根据旋转和平移的定义,直接求解.
解:图①经过轴对称变换得到图②;图①经过旋转变换得到图③;图①经过平移变换得到图④.
故答案为:轴对称;旋转;平移.
三.解答题(共7小题)
13.
【分析】连接对应点BB′、CC′,根据对应点的连线经过对称中心,则交点就是对称中心O点.
解:连接BB′,找BB′中点O或者连接BB′、CC′,交点为对称中心O.
如图所示:
( http: / / www.21cnjy.com )
14.
【分析】(1)根据中心对称图形的性质找出各顶点的对应点,然后顺次连接即可;
(2)根据三角形的三边关系求解即可.
解:(1)所画图形如下所示:
( http: / / www.21cnjy.com )
△ADE就是所作的图形.
(2)由(1)知:△ADE≌△BDC,
则CD=DE,AE=BC,
∴AE﹣AC<2CD<AE+AC,即BC﹣AC<2CD<BC+AC,
∴2<2CD<10,
解得:1<CD<5.
15.
【分析】(1)根据中心对称图形,画出所有可能的图形即可.
(2)根据是轴对称图形,不是中心对称图形,画出图形即可.
解:(1)在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形,答案如图所示;21*cnjy*com
( http: / / www.21cnjy.com )
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形,答案如图所示;www.21-cn-jy.com
( http: / / www.21cnjy.com )
16.
【分析】(1)利用旋转的性质得出,△ACC1的形状即可;
(2)利用关于点O成中心对称的性质得出对应点坐标即可;
(3)利用平移的性质得出平移方法即可.
解:(1)如图,∵AC=AC1,∠CAC1=90°,
∴△ACC1是等腰直角三角形;
(2)如图,△A2B2C2,即为所求;
(3)答案不唯一.如:
①先将△AB1C1向右平移5个单位,然后再向下平移6个单位.
②先将△AB1C1向下平移6个单位,然后再向右平移5个单位.
③将△AB1C1沿着点C1到点A2的方向,平移的距离为C1 A2的长度单位.
( http: / / www.21cnjy.com )
17.
【分析】(1)直接利用中心对称图形的定义分析得出答案;
(2)直接利用中心对称图形的定义得出对应点位置进而得出答案.
解:(1)如图a所示:图中阴影部分构成中心对称图形是①④,
故答案为:①④;
(2)如图b,△A1B1C1,即为所求.
( http: / / www.21cnjy.com )
18.
【分析】(1)根据图形平移的性质画出平移后的△A1B1C1即可;
(2)根据图形旋转的性质画出旋转后的△DE1F1即可.
解(1)如图所示:△A1B1C1即为所求;
(2)如图所示:△DE1F1即为所求;
( http: / / www.21cnjy.com )
19.
【分析】(1)根据三种全等变换翻折、平移、旋转的定义可知判断;
(2)根据平移的距离的定义可知AD=2,则DC=AC﹣AD;
(3)根据轴对称及三角形内角和定理得出.
解:(1)旋转;
(2)∵AD=2,
∴DC=AC﹣AD=3﹣2=1;
(3)∵把△ADE沿DE翻折,得到△FDE,
∴∠ADE=∠FDE,∠AED=∠FED,
在△DEF中,∠F=180°﹣(∠FDE+∠FED);
由平角定义知,∠BDF=180°﹣∠FDA=180°﹣2∠FDE,
∠CEF=180°﹣∠FEA=180°﹣2∠FED,
∴∠BDF+∠CEF=180°﹣2∠FDE+180°﹣2∠FED=2[180°﹣(∠FDE+∠FED)]
∴∠BDF+∠CEF=2∠F.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
