19.1.1 矩形的性质同步练习
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
19.1.1 矩形的性质同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.矩形的定义:有一个角是 直角 的平行四边形是矩形.
2.矩形的性质:
(1)矩形的对边平行且相等.
(2)矩形的四个角都是直角.
(3)矩形的对角线相等.
(4)从对称性上看,它既是中心对称图形,又是轴对称图形.
基础知识和能力拓展精练
一.选择题(共8小题)
1.矩形具有而平行四边形不一定具有的性质是( )
A.对角相等 B.对边相等 C.对角线相等 D.对角线互相平分
2.如图,在矩形ABCD中,E,F分别是 ( http: / / www.21cnjy.com )边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
( http: / / www.21cnjy.com )
A.8 ( http: / / www.21cnjy.com ) B.8 C.4 ( http: / / www.21cnjy.com ) D.6
3.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分△AFC的面积为( )
( http: / / www.21cnjy.com )
A.12 B.10 C.8 D.6
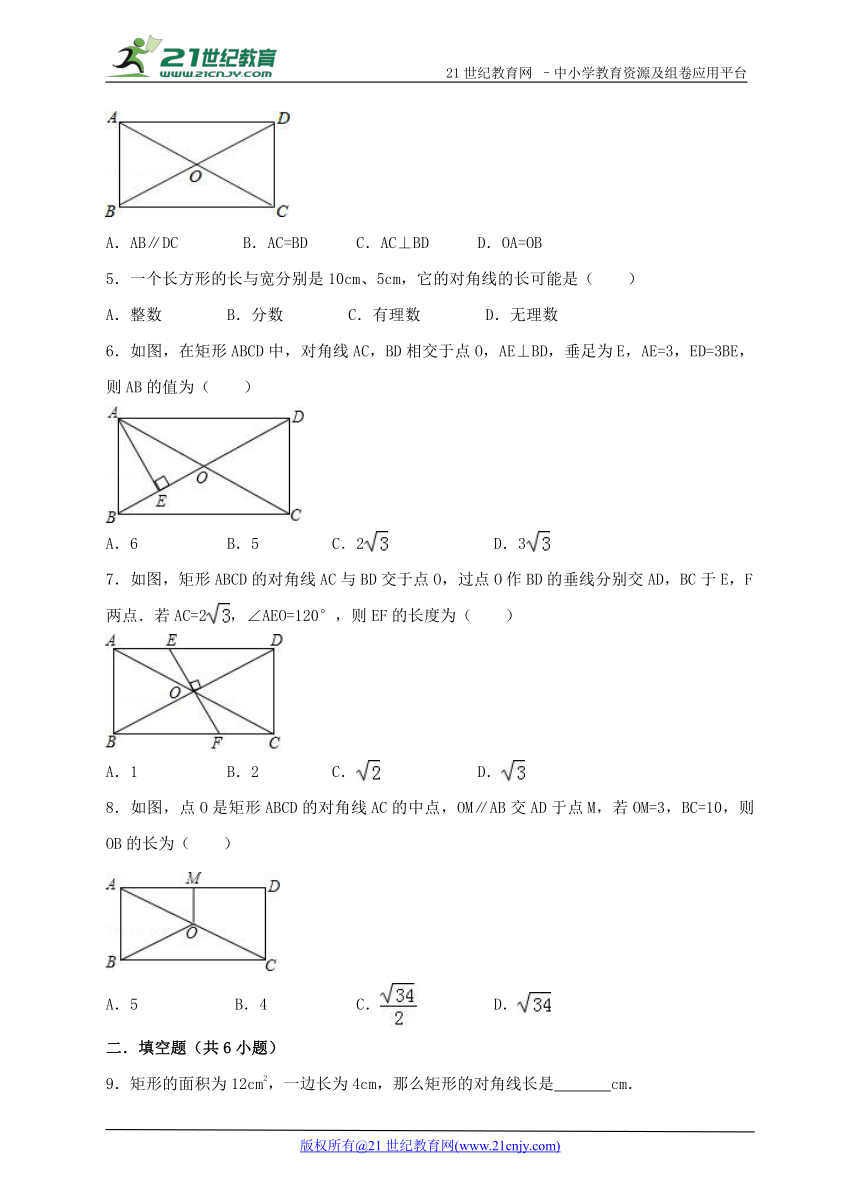
4.如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )
( http: / / www.21cnjy.com )
A.AB∥DC B.AC=BD C.AC⊥BD D.OA=OB
5.一个长方形的长与宽分别是10cm、5cm,它的对角线的长可能是( )
A.整数 B.分数 C.有理数 D.无理数
6.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD,垂足为E,AE=3,ED=3BE,则AB的值为( )21教育网
( http: / / www.21cnjy.com )
A.6 B.5 C.2 ( http: / / www.21cnjy.com ) D.3 ( http: / / www.21cnjy.com )
7.如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2 ( http: / / www.21cnjy.com ),∠AEO=120°,则EF的长度为( )21cnjy.com
( http: / / www.21cnjy.com )
A.1 B.2 C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
8.如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )21*cnjy*com
( http: / / www.21cnjy.com )
A.5 B.4 C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二.填空题(共6小题)
9.矩形的面积为12cm2,一边长为4cm,那么矩形的对角线长是 cm.
10.如图,矩形ABCD被分成四部分,其中△ABE、△ECF、△ADF的面积分别为2、3、4,则△AEF的面积为 .
( http: / / www.21cnjy.com )
11.如图,矩形ABCD中,AB= ( http: / / www.21cnjy.com ),AD=2.点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F.当△CDF是等腰三角形时,BE的长为 .
( http: / / www.21cnjy.com )
12.如图,在矩形ABCD中,AE⊥BD, ( http: / / www.21cnjy.com )垂足为E,若BE=OE=1cm,则∠AOB= ,AC= ,S矩形ABCD= .
( http: / / www.21cnjy.com )
13.如图,在矩形ABCD中,AE⊥BD.若∠DAE:∠BAE=3:1,则∠EAO= .
( http: / / www.21cnjy.com )
14.如图,在矩形ABCD中,AB=3,A ( http: / / www.21cnjy.com )D=4,P是AD上不与A、D重合的一动点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF的值为 .
( http: / / www.21cnjy.com )
三.解答题(共5小题)
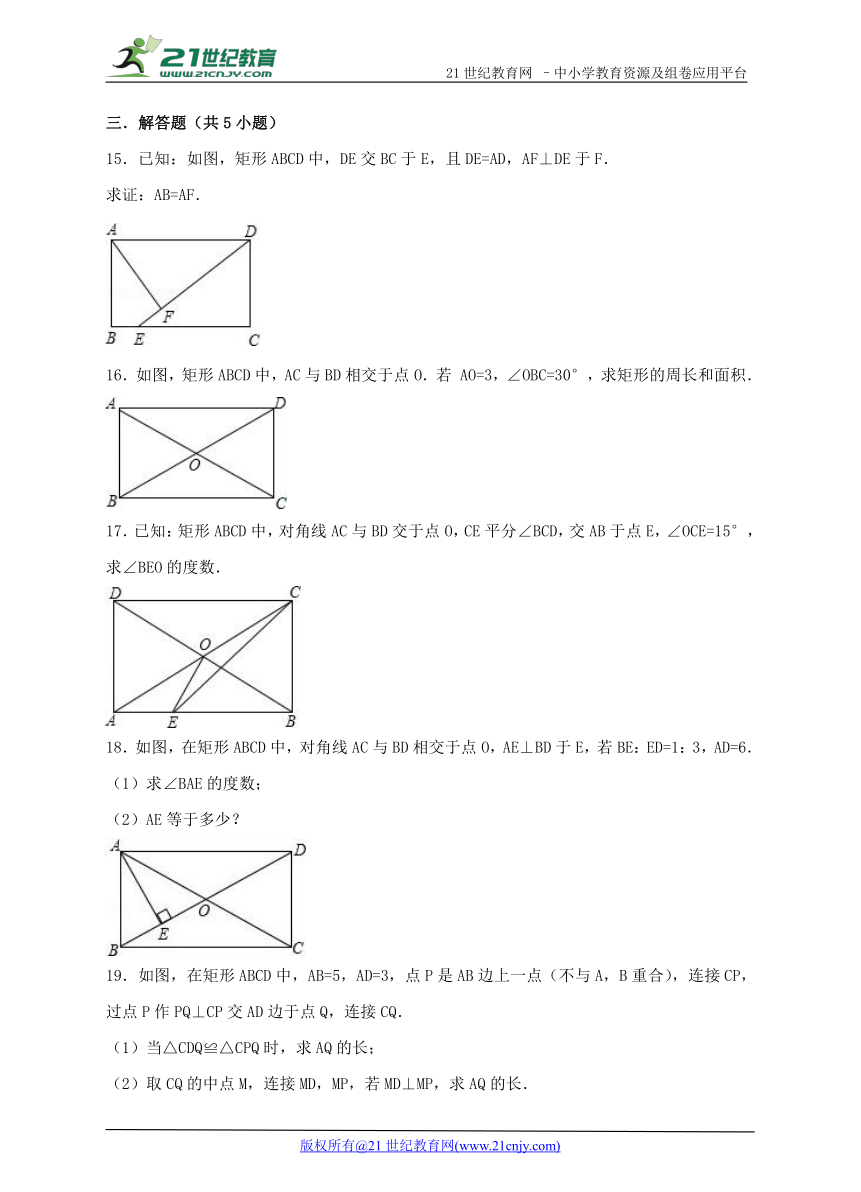
15.已知:如图,矩形ABCD中,DE交BC于E,且DE=AD,AF⊥DE于F.
求证:AB=AF.
( http: / / www.21cnjy.com )
16.如图,矩形ABCD中,AC与BD相交于点O.若 AO=3,∠OBC=30°,求矩形的周长和面积.
( http: / / www.21cnjy.com )
17.已知:矩形ABCD中,对角线AC与BD交于点O,CE平分∠BCD,交AB于点E,∠OCE=15°,求∠BEO的度数.2-1-c-n-j-y
( http: / / www.21cnjy.com )
18.如图,在矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD于E,若BE:ED=1:3,AD=6.
(1)求∠BAE的度数;
(2)AE等于多少?
( http: / / www.21cnjy.com )
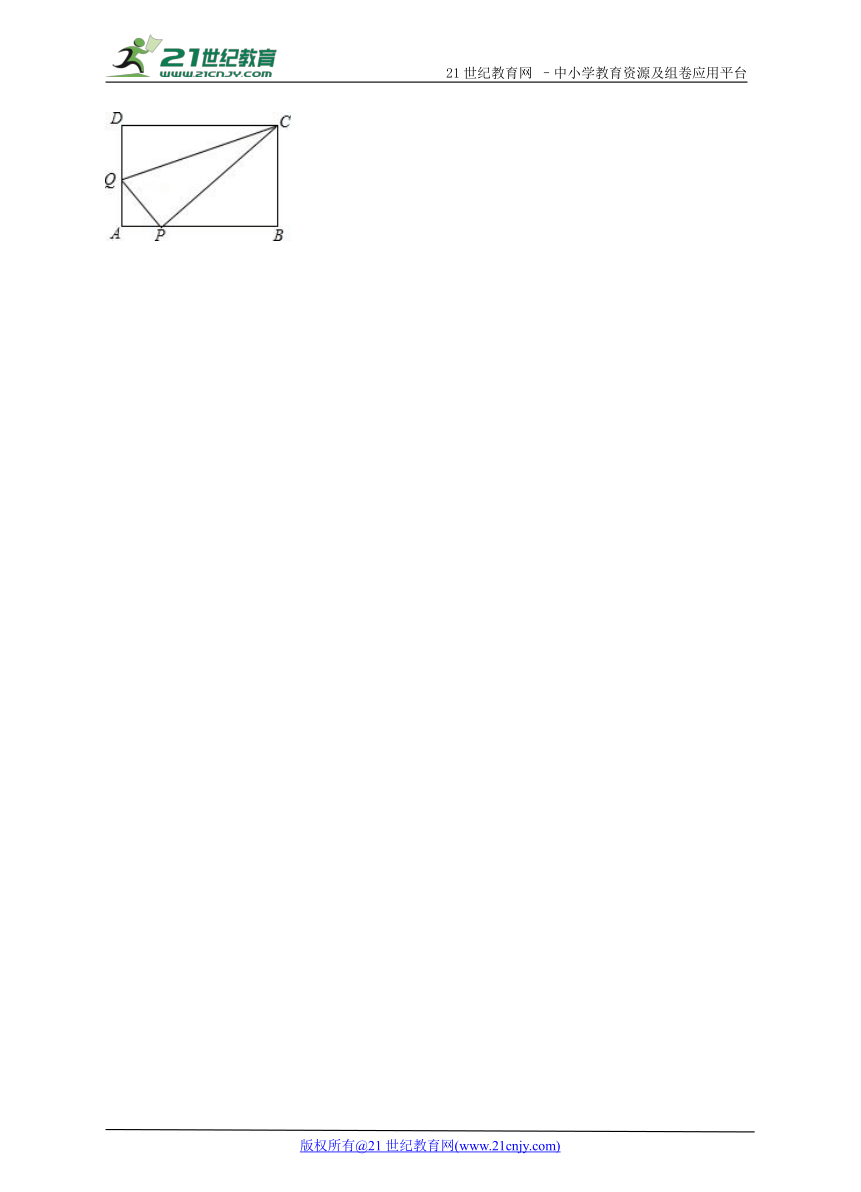
19.如图,在矩形ABCD ( http: / / www.21cnjy.com )中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.
(1)当△CDQ≌△CPQ时,求AQ的长;
(2)取CQ的中点M,连接MD,MP,若MD⊥MP,求AQ的长.
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共8小题)
1.
【分析】矩形的对角线互相平分且相等,而平行四边形的对角线互相平分,不一定相等.
解:矩形的对角线相等,而平行四边形的对角线不一定相等.
故选:C.
2.
【分析】连接OB,根据等腰三角形三线合 ( http: / / www.21cnjy.com )一的性质可得BO⊥EF,再根据矩形的性质可得OA=OB,根据等边对等角的性质可得∠BAC=∠ABO,再根据三角形的内角和定理列式求出∠ABO=30°,即∠BAC=30°,根据直角三角形30°角所对的直角边等于斜边的一半求出AC,再利用勾股定理列式计算即可求出AB.2·1·c·n·j·y
解:如图,连接OB,
∵BE=BF,OE=OF,
∴BO⊥EF,
∴在Rt△BEO中,∠BEF+∠ABO=90°,
由直角三角形斜边上的中线等于斜边上的一半可知:OA=OB=OC,
∴∠BAC=∠ABO,
又∵∠BEF=2∠BAC,
即2∠BAC+∠BAC=90°,
解得∠BAC=30°,
∴∠FCA=30°,
∴∠FBC=30°,
∵FC=2,
∴BC= ( http: / / www.21cnjy.com ),
∴AC=2BC=4 ( http: / / www.21cnjy.com ),
∴AB= ( http: / / www.21cnjy.com ),
故选:D.
( http: / / www.21cnjy.com )
3.
【分析】∵△AD′C≌△ABC,∴ ( http: / / www.21cnjy.com )△AD′F≌△CBF,得△AD′F与△CBF面积相等,设BF=x,列出关于x的关系式,解得x的值即可解题.21·世纪*教育网
解:∵△AD′C≌△ABC,
∴△AD′F≌△CBF,
∴△AD′F与△CBF面积相等,
设BF=x,则(8﹣x)2=x2+42,
64﹣16x+x2=x2+16,
16x=48,
解得x=3,
∴△AFC的面积= ( http: / / www.21cnjy.com )×4×8﹣ ( http: / / www.21cnjy.com )×3×4=10.
故选:B.
4.
【分析】根据矩形的性质推出即可.
∵四边形ABCD是矩形,
∴AB∥DC,AC=BD,OA=OB,不能推出AC⊥BD,
∴选项A、B、D正确,选项C错误;
故选:C.
5.
【分析】长方形的长、宽和对角线,构成一个直角三角形,可用勾股定理,求得对角线的长,再进行选择即可.
解:∵ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=5 ( http: / / www.21cnjy.com ),
∴对角线长是无理数.
故选:D.
6.
【分析】由在矩形ABCD中,AE⊥ ( http: / / www.21cnjy.com )BD于E,BE:ED=1:3,易证得△OAB是等边三角形,继而求得∠BAE的度数,由△OAB是等边三角形,求出∠ADE的度数,又由AE=3,即可求得AB的长.21·cn·jy·com
解:∵四边形ABCD是矩形,
∴OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵BE:ED=1:3,
∴BE:OB=1:2,
∵AE⊥BD,
∴AB=OA,
∴OA=AB=OB,
即△OAB是等边三角形,
∴∠ABD=60°,
∵AE⊥BD,AE=3,
∴AB= ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com ),
故选:C.
( http: / / www.21cnjy.com )
7.
【分析】先根据矩形的性质,推理得到∠EDO=30°,再根据Rt△DOE求得OE的长,即可得到EF的长.21*cnjy*com
解:∵∠AEO=120°,∠DOE=90°,
∴∠EDO=30°,
又∵AC=2 ( http: / / www.21cnjy.com ),
∴DO= ( http: / / www.21cnjy.com )BD= ( http: / / www.21cnjy.com )AC= ( http: / / www.21cnjy.com ),
∴Rt△DOE中,OE=tan30°×DO=1,
同理可得,Rt△BOF中,OF=1,
∴EF=2,
故选:B.
8.
【分析】已知OM是△ADC的中位线,再结合已 ( http: / / www.21cnjy.com )知条件则DC的长可求出,所以利用勾股定理可求出AC的长,由直角三角形斜边上中线的性质则BO的长即可求出.
解:∵四边形ABCD是矩形,
∴∠D=90°,
∵O是矩形ABCD的对角线AC的中点,OM∥AB,
∴OM是△ADC的中位线,
∵OM=3,
∴DC=6,
∵AD=BC=10,
∴AC= ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com ),
∴BO= ( http: / / www.21cnjy.com )AC= ( http: / / www.21cnjy.com ),
故选:D.
二.填空题(共6小题)
9.
【分析】由矩形的面积与边长,可求另一边长,进而利用勾股定理求矩形的对角线.
解:∵矩形的面积为12cm2,一边长为4cm,
∴另一边为3cm,
∴对角线长为 ( http: / / www.21cnjy.com )=5cm.
故答案为5.
10.
【分析】首先设AB=a,BC=b,由△CEF,△ABE,△ADF的面积分别是2,3,4可得S△ABE= ( http: / / www.21cnjy.com )×a×BE=2,S△CEF= ( http: / / www.21cnjy.com )×EC×FC=3,则可得S△ADF= ( http: / / www.21cnjy.com )×(a﹣ ( http: / / www.21cnjy.com ))×b=4,继而求得ab的值.
解:设AB=a,BC=b,
∵△CEF,△ABE,△ADF的面积分别是2,3,4,
∴S△ABE= ( http: / / www.21cnjy.com )×a×BE=2,
∴BE= ( http: / / www.21cnjy.com ),
∴EC=BC﹣BE=b﹣ ( http: / / www.21cnjy.com ),
∵S△CEF= ( http: / / www.21cnjy.com )×EC×FC=3,
∴FC= ( http: / / www.21cnjy.com ),
∴DF=CD﹣CF=a﹣ ( http: / / www.21cnjy.com ),
∴S△ADF= ( http: / / www.21cnjy.com )×(a﹣ ( http: / / www.21cnjy.com ))×b=4,
∴(ab)2﹣18ab+32=0,
解得:ab=16或ab=2(不合题意,舍去),
∴S△AEF=16﹣3﹣4﹣2=7,
故答案为:7.
11.
【分析】过点C作CM⊥DF ( http: / / www.21cnjy.com ),垂足为点M,判断△CDF是等腰三角形,要分类讨论,①CF=CD;②DF=DC;③FD=FC,根据相似三角形的性质进行求解.【来源:21cnj*y.co*m】
解:①CF=CD时,过点C作CM⊥DF,垂足为点M,
则CM∥AE,DM=MF,(1分)
延长CM交AD于点G,
∴AG=GD=1,
∴CE=1,
∴当BE=1时,△CDF是等腰三角形;
②DF=DC时,则DC=DF= ( http: / / www.21cnjy.com ),
∵DF⊥AE,AD=2,
∴∠DAE=45°,(1分)
则BE= ( http: / / www.21cnjy.com ),
∴当BE= ( http: / / www.21cnjy.com )时,△CDF是等腰三角形;
③FD=FC时,则点F在CD的垂直平分线上,故F为AE中点.
∵AB= ( http: / / www.21cnjy.com ),BE=x,
∴AE= ( http: / / www.21cnjy.com ),
AF= ( http: / / www.21cnjy.com ),
∵△ADF∽△EAB,
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com ),
x2﹣4x+2=0,
解得:x=2± ( http: / / www.21cnjy.com ),
∴当BE=2﹣ ( http: / / www.21cnjy.com )时,△CDF是等腰三角形.
综上,当BE=1、 ( http: / / www.21cnjy.com )、2﹣ ( http: / / www.21cnjy.com )时,△CDF是等腰三角形.
故答案为:1、 ( http: / / www.21cnjy.com )、2﹣ ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
12.
【分析】根据矩形的性质得出AC=2AO,OA=OB,得出等边三角形AOB,求出AB=OA=OB=2cm,求出BC,即可得出答案.【版权所有:21教育】
解:∵BE=OE=1cm,
∴OB=2cm,
∵四边形ABCD是矩形,
∴∠ABC=90°,AO=OC,BO=DO,AC=BD,
∴OA=OB,
∵AE⊥BD,BE=OE,
∴AB=AO,
∴OA=AB=OB=2cm,
∴△AOB是等边三角形,
∴∠AOB=60°,OA=OB=2cm,
∴AC=2AO=4cm,
由勾股定理得:BC= ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com )(cm),
∴S矩形ABCD=BC×AB=2 ( http: / / www.21cnjy.com )cm×2cm=4 ( http: / / www.21cnjy.com )cm2
故答案为:60°,4cm,4 ( http: / / www.21cnjy.com )cm2.
13.
【分析】根据矩形性质得出AC=BD,OA=OC= ( http: / / www.21cnjy.com )AC,BO=DO= ( http: / / www.21cnjy.com )BD,∠BAD=90°,推出OA=OB,求出∠DAE=67.5°,∠BAE=22.5°,求出∠ABO=67.5°,∠OAB=∠OBA=67.5°,即可求出答案.
解:∵四边形ABCD是矩形,
∴AC=BD,OA=OC= ( http: / / www.21cnjy.com )AC,BO=DO= ( http: / / www.21cnjy.com )BD,∠BAD=90°,
∴OA=OB,
∵∠DAE:∠BAE=3:1,
∴∠DAE=67.5°,∠BAE=22.5°,
∵AE⊥BD,
∴∠AEB=90°,
∴∠ABO=90°﹣22.5°=67.5°,
∵OA=OB,
∴∠OAB=∠OBA=67.5°,
∴∠EAO=∠OAB﹣∠BAE=67.5°﹣22.5°=45°,
故答案为:45°.
14.
【分析】连接OP,过点A ( http: / / www.21cnjy.com )作AG⊥BD于G,利用勾股定理列式求出BD,再利用三角形的面积求出AG,然后根据△AOD的面积求出PE+PF=AG.【来源:21·世纪·教育·网】
解:如图,连接OP,过点A作AG⊥BD于G,
∵AB=3,AD=4,
∴BD= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=5,
S△ABD= ( http: / / www.21cnjy.com )AB AD= ( http: / / www.21cnjy.com )BD AG,
即 ( http: / / www.21cnjy.com )×3×4= ( http: / / www.21cnjy.com )×5×AG,
解得AG= ( http: / / www.21cnjy.com ),
在矩形ABCD中,OA=OD,
∵S△AOD= ( http: / / www.21cnjy.com )OA PE+ ( http: / / www.21cnjy.com )OD PF= ( http: / / www.21cnjy.com )OD AG,
∴PE+PF=AG= ( http: / / www.21cnjy.com ).
故PE+PF= ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
三.解答题(共5小题)
15.
【分析】根据已知及矩形的性质利用AAS判定△ADF≌△DEC,从而得到AF=DC,因为DC=AB,所以AF=AB.www-2-1-cnjy-com
证明:∵AF⊥DE.
∴∠AFE=90°.
∵在矩形ABCD中,AD∥BC,∠C=90°.
∴∠ADF=∠DEC.
∴∠AFE=∠C=90°.
∵AD=DE.
∴△ADF≌△DEC.
∴AF=DC.
∵DC=AB.
∴AF=AB.
16.
【分析】根据矩形的性质得出∠ABC=9 ( http: / / www.21cnjy.com )0°,AD=BC,AB=DC,AO=OC,OB=OD,AC=BD,求出AC=BD=2AO=6,OB=OC,求出AB、BC,最后求出周长和面积即可.21教育名师原创作品
解:∵四边形ABCD是矩形,AO=3,
∴∠ABC=90°,AD=BC,AB=DC,AO=OC,OB=OD,AC=BD,
∴AC=BD=2AO=6,OB=OC,
∴AB= ( http: / / www.21cnjy.com )AC=3,
由勾股定理得:BC=3 ( http: / / www.21cnjy.com ),
∴AB=DC=3,AD=BC=3 ( http: / / www.21cnjy.com ),
∴矩形ABCD的周长是AB+BC+CD+AD=6+6 ( http: / / www.21cnjy.com ),
矩形ABCD的面积是AB×BC=3×3 ( http: / / www.21cnjy.com )=9 ( http: / / www.21cnjy.com ).
17.
【分析】根据矩形性质得出∠DCB=90 ( http: / / www.21cnjy.com )°,AB∥CD,AO=OC=OB=OD,求出BC=BE,得出等边三角形COB,得出BO=OE,求出∠OBE=30°,根据等腰三角形性质和三角形内角和定理求出即可.
解:∵四边形ABCD是矩形,
∴∠DCB=90°,DC∥AB,
∴∠DCE=∠CEB,
∵CE平分∠DCB,
∴∠BCE=∠DCE=45°,
∴∠BCE=∠CEB,
∴BE=BC,
∵∠DCE=45°,∠OCE=15°,
∴∠DCO=30°,
∴∠BCO﹣90°﹣30°=60°,
∵四边形ABCD是矩形,
∴AC=2AO=2OC,BD=2BO=2DO,AC=BD,
∴AO=OC=CO=BO,
∴△BOC是等边三角形,
∴BC=OB=BE,
∵DC∥AB,
∴∠CAB=∠DBA=30°,
∴∠BEO=∠BOE= ( http: / / www.21cnjy.com )(180°﹣∠DBA)= ( http: / / www.21cnjy.com )×(180°﹣30°)=75°.
18.
【分析】(1)由在矩形ABCD中,AE⊥BD于E,BE:ED=1:3,易证得△OAB是等边三角形,继而求得∠BAE的度数;21世纪教育网版权所有
(2)由△OAB是等边三角形,易求得∠ADE=30°,又由AD=6,即可求得AE的长.
解:(1)∵四边形ABCD是矩形,
∴OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵BE:ED=1:3,
∴BE:OB=1:2,
∵AE⊥BD,
∴AB=OA,
∴OA=AB=OB,
即△OAB是等边三角形,
∴∠BAE=30°;
(2)∵△OAB是等边三角形,
∴∠ABD=60°,
∴∠ADE=90°﹣∠ABD=30°,
∵AE⊥BD,AD=6,
∴AE= ( http: / / www.21cnjy.com )AD=3.
19.
【分析】(1)根据全等三角形的性质求得DQ=PQ,PC=DC=5,然后利用勾股定理即可求得;
(2)方法1、过M作EF⊥CD于F,则EF⊥AB,先证得△MDF≌△PME,求得ME=DF= ( http: / / www.21cnjy.com ),然后根据梯形的中位线的性质定理即可求得.www.21-cn-jy.com
方法2、先利用三角形的外角和∠DMP=90°,得出∠DCP=90°,得出BP=BC=3,再判断出AQ=AP=2即可.【出处:21教育名师】
解:(1)∵△CDQ≌△CPQ,
∴DQ=PQ,PC=DC,
∵AB=DC=5,AD=BC=3,
∴PC=5,
在Rt△PBC中,PB= ( http: / / www.21cnjy.com )=4,
∴PA=AB﹣PB=5﹣4=1,
设AQ=x,则DQ=PQ=3﹣x,
在Rt△PAQ中,(3﹣x)2=x2+12,
解得x= ( http: / / www.21cnjy.com ),
∴AQ= ( http: / / www.21cnjy.com ).
(2)方法1,如图2,过M作EF⊥CD于F,则EF⊥AB,
∵MD⊥MP,
∴∠PMD=90°,
∴∠PME+∠DMF=90°,
∵∠FDM+∠DMF=90°,
∴∠MDF=∠PME,
∵M是QC的中点,
∴DM= ( http: / / www.21cnjy.com )QC,PM= ( http: / / www.21cnjy.com )QC,
∴DM=PM,
在△MDF和△PME中,
( http: / / www.21cnjy.com ),
∴△MDF≌△PME(AAS),
∴ME=DF,PE=MF,
∵EF⊥CD,AD⊥CD,
∴EF∥AD,
∵QM=MC,
∴DF=CF= ( http: / / www.21cnjy.com )DC= ( http: / / www.21cnjy.com ),
∴ME= ( http: / / www.21cnjy.com ),
∵ME是梯形ABCQ的中位线,
∴2ME=AQ+BC,即5=AQ+3,
∴AQ=2.
( http: / / www.21cnjy.com )
方法2、∵点M是Rt△CDQ的斜边CQ中点,
∴DM=CM,
∴∠DMQ=2∠DCQ,
∵点M是Rt△CPQ的斜边的中点,
∴MP=CM,
∴∠PMQ=2∠PCQ,
∵∠DMP=90°,
∴2∠DCQ+2∠PCQ=90°,
∴∠PCD=45°,°∠BCP=90°﹣45°=45°,
∴∠BPC=45°=∠BCP,∴BP=BC=3,
∵∠CPQ=90°,
∴∠APQ=180°﹣90°﹣45°=45°,
∴∠AQP=90°﹣45°=45°=∠APQ,
∴AQ=AP=2.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
19.1.1 矩形的性质同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.矩形的定义:有一个角是 直角 的平行四边形是矩形.
2.矩形的性质:
(1)矩形的对边平行且相等.
(2)矩形的四个角都是直角.
(3)矩形的对角线相等.
(4)从对称性上看,它既是中心对称图形,又是轴对称图形.
基础知识和能力拓展精练
一.选择题(共8小题)
1.矩形具有而平行四边形不一定具有的性质是( )
A.对角相等 B.对边相等 C.对角线相等 D.对角线互相平分
2.如图,在矩形ABCD中,E,F分别是 ( http: / / www.21cnjy.com )边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
( http: / / www.21cnjy.com )
A.8 ( http: / / www.21cnjy.com ) B.8 C.4 ( http: / / www.21cnjy.com ) D.6
3.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分△AFC的面积为( )
( http: / / www.21cnjy.com )
A.12 B.10 C.8 D.6
4.如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )
( http: / / www.21cnjy.com )
A.AB∥DC B.AC=BD C.AC⊥BD D.OA=OB
5.一个长方形的长与宽分别是10cm、5cm,它的对角线的长可能是( )
A.整数 B.分数 C.有理数 D.无理数
6.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD,垂足为E,AE=3,ED=3BE,则AB的值为( )21教育网
( http: / / www.21cnjy.com )
A.6 B.5 C.2 ( http: / / www.21cnjy.com ) D.3 ( http: / / www.21cnjy.com )
7.如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2 ( http: / / www.21cnjy.com ),∠AEO=120°,则EF的长度为( )21cnjy.com
( http: / / www.21cnjy.com )
A.1 B.2 C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
8.如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )21*cnjy*com
( http: / / www.21cnjy.com )
A.5 B.4 C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二.填空题(共6小题)
9.矩形的面积为12cm2,一边长为4cm,那么矩形的对角线长是 cm.
10.如图,矩形ABCD被分成四部分,其中△ABE、△ECF、△ADF的面积分别为2、3、4,则△AEF的面积为 .
( http: / / www.21cnjy.com )
11.如图,矩形ABCD中,AB= ( http: / / www.21cnjy.com ),AD=2.点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F.当△CDF是等腰三角形时,BE的长为 .
( http: / / www.21cnjy.com )
12.如图,在矩形ABCD中,AE⊥BD, ( http: / / www.21cnjy.com )垂足为E,若BE=OE=1cm,则∠AOB= ,AC= ,S矩形ABCD= .
( http: / / www.21cnjy.com )
13.如图,在矩形ABCD中,AE⊥BD.若∠DAE:∠BAE=3:1,则∠EAO= .
( http: / / www.21cnjy.com )
14.如图,在矩形ABCD中,AB=3,A ( http: / / www.21cnjy.com )D=4,P是AD上不与A、D重合的一动点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF的值为 .
( http: / / www.21cnjy.com )
三.解答题(共5小题)
15.已知:如图,矩形ABCD中,DE交BC于E,且DE=AD,AF⊥DE于F.
求证:AB=AF.
( http: / / www.21cnjy.com )
16.如图,矩形ABCD中,AC与BD相交于点O.若 AO=3,∠OBC=30°,求矩形的周长和面积.
( http: / / www.21cnjy.com )
17.已知:矩形ABCD中,对角线AC与BD交于点O,CE平分∠BCD,交AB于点E,∠OCE=15°,求∠BEO的度数.2-1-c-n-j-y
( http: / / www.21cnjy.com )
18.如图,在矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD于E,若BE:ED=1:3,AD=6.
(1)求∠BAE的度数;
(2)AE等于多少?
( http: / / www.21cnjy.com )
19.如图,在矩形ABCD ( http: / / www.21cnjy.com )中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.
(1)当△CDQ≌△CPQ时,求AQ的长;
(2)取CQ的中点M,连接MD,MP,若MD⊥MP,求AQ的长.
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共8小题)
1.
【分析】矩形的对角线互相平分且相等,而平行四边形的对角线互相平分,不一定相等.
解:矩形的对角线相等,而平行四边形的对角线不一定相等.
故选:C.
2.
【分析】连接OB,根据等腰三角形三线合 ( http: / / www.21cnjy.com )一的性质可得BO⊥EF,再根据矩形的性质可得OA=OB,根据等边对等角的性质可得∠BAC=∠ABO,再根据三角形的内角和定理列式求出∠ABO=30°,即∠BAC=30°,根据直角三角形30°角所对的直角边等于斜边的一半求出AC,再利用勾股定理列式计算即可求出AB.2·1·c·n·j·y
解:如图,连接OB,
∵BE=BF,OE=OF,
∴BO⊥EF,
∴在Rt△BEO中,∠BEF+∠ABO=90°,
由直角三角形斜边上的中线等于斜边上的一半可知:OA=OB=OC,
∴∠BAC=∠ABO,
又∵∠BEF=2∠BAC,
即2∠BAC+∠BAC=90°,
解得∠BAC=30°,
∴∠FCA=30°,
∴∠FBC=30°,
∵FC=2,
∴BC= ( http: / / www.21cnjy.com ),
∴AC=2BC=4 ( http: / / www.21cnjy.com ),
∴AB= ( http: / / www.21cnjy.com ),
故选:D.
( http: / / www.21cnjy.com )
3.
【分析】∵△AD′C≌△ABC,∴ ( http: / / www.21cnjy.com )△AD′F≌△CBF,得△AD′F与△CBF面积相等,设BF=x,列出关于x的关系式,解得x的值即可解题.21·世纪*教育网
解:∵△AD′C≌△ABC,
∴△AD′F≌△CBF,
∴△AD′F与△CBF面积相等,
设BF=x,则(8﹣x)2=x2+42,
64﹣16x+x2=x2+16,
16x=48,
解得x=3,
∴△AFC的面积= ( http: / / www.21cnjy.com )×4×8﹣ ( http: / / www.21cnjy.com )×3×4=10.
故选:B.
4.
【分析】根据矩形的性质推出即可.
∵四边形ABCD是矩形,
∴AB∥DC,AC=BD,OA=OB,不能推出AC⊥BD,
∴选项A、B、D正确,选项C错误;
故选:C.
5.
【分析】长方形的长、宽和对角线,构成一个直角三角形,可用勾股定理,求得对角线的长,再进行选择即可.
解:∵ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=5 ( http: / / www.21cnjy.com ),
∴对角线长是无理数.
故选:D.
6.
【分析】由在矩形ABCD中,AE⊥ ( http: / / www.21cnjy.com )BD于E,BE:ED=1:3,易证得△OAB是等边三角形,继而求得∠BAE的度数,由△OAB是等边三角形,求出∠ADE的度数,又由AE=3,即可求得AB的长.21·cn·jy·com
解:∵四边形ABCD是矩形,
∴OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵BE:ED=1:3,
∴BE:OB=1:2,
∵AE⊥BD,
∴AB=OA,
∴OA=AB=OB,
即△OAB是等边三角形,
∴∠ABD=60°,
∵AE⊥BD,AE=3,
∴AB= ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com ),
故选:C.
( http: / / www.21cnjy.com )
7.
【分析】先根据矩形的性质,推理得到∠EDO=30°,再根据Rt△DOE求得OE的长,即可得到EF的长.21*cnjy*com
解:∵∠AEO=120°,∠DOE=90°,
∴∠EDO=30°,
又∵AC=2 ( http: / / www.21cnjy.com ),
∴DO= ( http: / / www.21cnjy.com )BD= ( http: / / www.21cnjy.com )AC= ( http: / / www.21cnjy.com ),
∴Rt△DOE中,OE=tan30°×DO=1,
同理可得,Rt△BOF中,OF=1,
∴EF=2,
故选:B.
8.
【分析】已知OM是△ADC的中位线,再结合已 ( http: / / www.21cnjy.com )知条件则DC的长可求出,所以利用勾股定理可求出AC的长,由直角三角形斜边上中线的性质则BO的长即可求出.
解:∵四边形ABCD是矩形,
∴∠D=90°,
∵O是矩形ABCD的对角线AC的中点,OM∥AB,
∴OM是△ADC的中位线,
∵OM=3,
∴DC=6,
∵AD=BC=10,
∴AC= ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com ),
∴BO= ( http: / / www.21cnjy.com )AC= ( http: / / www.21cnjy.com ),
故选:D.
二.填空题(共6小题)
9.
【分析】由矩形的面积与边长,可求另一边长,进而利用勾股定理求矩形的对角线.
解:∵矩形的面积为12cm2,一边长为4cm,
∴另一边为3cm,
∴对角线长为 ( http: / / www.21cnjy.com )=5cm.
故答案为5.
10.
【分析】首先设AB=a,BC=b,由△CEF,△ABE,△ADF的面积分别是2,3,4可得S△ABE= ( http: / / www.21cnjy.com )×a×BE=2,S△CEF= ( http: / / www.21cnjy.com )×EC×FC=3,则可得S△ADF= ( http: / / www.21cnjy.com )×(a﹣ ( http: / / www.21cnjy.com ))×b=4,继而求得ab的值.
解:设AB=a,BC=b,
∵△CEF,△ABE,△ADF的面积分别是2,3,4,
∴S△ABE= ( http: / / www.21cnjy.com )×a×BE=2,
∴BE= ( http: / / www.21cnjy.com ),
∴EC=BC﹣BE=b﹣ ( http: / / www.21cnjy.com ),
∵S△CEF= ( http: / / www.21cnjy.com )×EC×FC=3,
∴FC= ( http: / / www.21cnjy.com ),
∴DF=CD﹣CF=a﹣ ( http: / / www.21cnjy.com ),
∴S△ADF= ( http: / / www.21cnjy.com )×(a﹣ ( http: / / www.21cnjy.com ))×b=4,
∴(ab)2﹣18ab+32=0,
解得:ab=16或ab=2(不合题意,舍去),
∴S△AEF=16﹣3﹣4﹣2=7,
故答案为:7.
11.
【分析】过点C作CM⊥DF ( http: / / www.21cnjy.com ),垂足为点M,判断△CDF是等腰三角形,要分类讨论,①CF=CD;②DF=DC;③FD=FC,根据相似三角形的性质进行求解.【来源:21cnj*y.co*m】
解:①CF=CD时,过点C作CM⊥DF,垂足为点M,
则CM∥AE,DM=MF,(1分)
延长CM交AD于点G,
∴AG=GD=1,
∴CE=1,
∴当BE=1时,△CDF是等腰三角形;
②DF=DC时,则DC=DF= ( http: / / www.21cnjy.com ),
∵DF⊥AE,AD=2,
∴∠DAE=45°,(1分)
则BE= ( http: / / www.21cnjy.com ),
∴当BE= ( http: / / www.21cnjy.com )时,△CDF是等腰三角形;
③FD=FC时,则点F在CD的垂直平分线上,故F为AE中点.
∵AB= ( http: / / www.21cnjy.com ),BE=x,
∴AE= ( http: / / www.21cnjy.com ),
AF= ( http: / / www.21cnjy.com ),
∵△ADF∽△EAB,
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com ),
x2﹣4x+2=0,
解得:x=2± ( http: / / www.21cnjy.com ),
∴当BE=2﹣ ( http: / / www.21cnjy.com )时,△CDF是等腰三角形.
综上,当BE=1、 ( http: / / www.21cnjy.com )、2﹣ ( http: / / www.21cnjy.com )时,△CDF是等腰三角形.
故答案为:1、 ( http: / / www.21cnjy.com )、2﹣ ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
12.
【分析】根据矩形的性质得出AC=2AO,OA=OB,得出等边三角形AOB,求出AB=OA=OB=2cm,求出BC,即可得出答案.【版权所有:21教育】
解:∵BE=OE=1cm,
∴OB=2cm,
∵四边形ABCD是矩形,
∴∠ABC=90°,AO=OC,BO=DO,AC=BD,
∴OA=OB,
∵AE⊥BD,BE=OE,
∴AB=AO,
∴OA=AB=OB=2cm,
∴△AOB是等边三角形,
∴∠AOB=60°,OA=OB=2cm,
∴AC=2AO=4cm,
由勾股定理得:BC= ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com )(cm),
∴S矩形ABCD=BC×AB=2 ( http: / / www.21cnjy.com )cm×2cm=4 ( http: / / www.21cnjy.com )cm2
故答案为:60°,4cm,4 ( http: / / www.21cnjy.com )cm2.
13.
【分析】根据矩形性质得出AC=BD,OA=OC= ( http: / / www.21cnjy.com )AC,BO=DO= ( http: / / www.21cnjy.com )BD,∠BAD=90°,推出OA=OB,求出∠DAE=67.5°,∠BAE=22.5°,求出∠ABO=67.5°,∠OAB=∠OBA=67.5°,即可求出答案.
解:∵四边形ABCD是矩形,
∴AC=BD,OA=OC= ( http: / / www.21cnjy.com )AC,BO=DO= ( http: / / www.21cnjy.com )BD,∠BAD=90°,
∴OA=OB,
∵∠DAE:∠BAE=3:1,
∴∠DAE=67.5°,∠BAE=22.5°,
∵AE⊥BD,
∴∠AEB=90°,
∴∠ABO=90°﹣22.5°=67.5°,
∵OA=OB,
∴∠OAB=∠OBA=67.5°,
∴∠EAO=∠OAB﹣∠BAE=67.5°﹣22.5°=45°,
故答案为:45°.
14.
【分析】连接OP,过点A ( http: / / www.21cnjy.com )作AG⊥BD于G,利用勾股定理列式求出BD,再利用三角形的面积求出AG,然后根据△AOD的面积求出PE+PF=AG.【来源:21·世纪·教育·网】
解:如图,连接OP,过点A作AG⊥BD于G,
∵AB=3,AD=4,
∴BD= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=5,
S△ABD= ( http: / / www.21cnjy.com )AB AD= ( http: / / www.21cnjy.com )BD AG,
即 ( http: / / www.21cnjy.com )×3×4= ( http: / / www.21cnjy.com )×5×AG,
解得AG= ( http: / / www.21cnjy.com ),
在矩形ABCD中,OA=OD,
∵S△AOD= ( http: / / www.21cnjy.com )OA PE+ ( http: / / www.21cnjy.com )OD PF= ( http: / / www.21cnjy.com )OD AG,
∴PE+PF=AG= ( http: / / www.21cnjy.com ).
故PE+PF= ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
三.解答题(共5小题)
15.
【分析】根据已知及矩形的性质利用AAS判定△ADF≌△DEC,从而得到AF=DC,因为DC=AB,所以AF=AB.www-2-1-cnjy-com
证明:∵AF⊥DE.
∴∠AFE=90°.
∵在矩形ABCD中,AD∥BC,∠C=90°.
∴∠ADF=∠DEC.
∴∠AFE=∠C=90°.
∵AD=DE.
∴△ADF≌△DEC.
∴AF=DC.
∵DC=AB.
∴AF=AB.
16.
【分析】根据矩形的性质得出∠ABC=9 ( http: / / www.21cnjy.com )0°,AD=BC,AB=DC,AO=OC,OB=OD,AC=BD,求出AC=BD=2AO=6,OB=OC,求出AB、BC,最后求出周长和面积即可.21教育名师原创作品
解:∵四边形ABCD是矩形,AO=3,
∴∠ABC=90°,AD=BC,AB=DC,AO=OC,OB=OD,AC=BD,
∴AC=BD=2AO=6,OB=OC,
∴AB= ( http: / / www.21cnjy.com )AC=3,
由勾股定理得:BC=3 ( http: / / www.21cnjy.com ),
∴AB=DC=3,AD=BC=3 ( http: / / www.21cnjy.com ),
∴矩形ABCD的周长是AB+BC+CD+AD=6+6 ( http: / / www.21cnjy.com ),
矩形ABCD的面积是AB×BC=3×3 ( http: / / www.21cnjy.com )=9 ( http: / / www.21cnjy.com ).
17.
【分析】根据矩形性质得出∠DCB=90 ( http: / / www.21cnjy.com )°,AB∥CD,AO=OC=OB=OD,求出BC=BE,得出等边三角形COB,得出BO=OE,求出∠OBE=30°,根据等腰三角形性质和三角形内角和定理求出即可.
解:∵四边形ABCD是矩形,
∴∠DCB=90°,DC∥AB,
∴∠DCE=∠CEB,
∵CE平分∠DCB,
∴∠BCE=∠DCE=45°,
∴∠BCE=∠CEB,
∴BE=BC,
∵∠DCE=45°,∠OCE=15°,
∴∠DCO=30°,
∴∠BCO﹣90°﹣30°=60°,
∵四边形ABCD是矩形,
∴AC=2AO=2OC,BD=2BO=2DO,AC=BD,
∴AO=OC=CO=BO,
∴△BOC是等边三角形,
∴BC=OB=BE,
∵DC∥AB,
∴∠CAB=∠DBA=30°,
∴∠BEO=∠BOE= ( http: / / www.21cnjy.com )(180°﹣∠DBA)= ( http: / / www.21cnjy.com )×(180°﹣30°)=75°.
18.
【分析】(1)由在矩形ABCD中,AE⊥BD于E,BE:ED=1:3,易证得△OAB是等边三角形,继而求得∠BAE的度数;21世纪教育网版权所有
(2)由△OAB是等边三角形,易求得∠ADE=30°,又由AD=6,即可求得AE的长.
解:(1)∵四边形ABCD是矩形,
∴OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵BE:ED=1:3,
∴BE:OB=1:2,
∵AE⊥BD,
∴AB=OA,
∴OA=AB=OB,
即△OAB是等边三角形,
∴∠BAE=30°;
(2)∵△OAB是等边三角形,
∴∠ABD=60°,
∴∠ADE=90°﹣∠ABD=30°,
∵AE⊥BD,AD=6,
∴AE= ( http: / / www.21cnjy.com )AD=3.
19.
【分析】(1)根据全等三角形的性质求得DQ=PQ,PC=DC=5,然后利用勾股定理即可求得;
(2)方法1、过M作EF⊥CD于F,则EF⊥AB,先证得△MDF≌△PME,求得ME=DF= ( http: / / www.21cnjy.com ),然后根据梯形的中位线的性质定理即可求得.www.21-cn-jy.com
方法2、先利用三角形的外角和∠DMP=90°,得出∠DCP=90°,得出BP=BC=3,再判断出AQ=AP=2即可.【出处:21教育名师】
解:(1)∵△CDQ≌△CPQ,
∴DQ=PQ,PC=DC,
∵AB=DC=5,AD=BC=3,
∴PC=5,
在Rt△PBC中,PB= ( http: / / www.21cnjy.com )=4,
∴PA=AB﹣PB=5﹣4=1,
设AQ=x,则DQ=PQ=3﹣x,
在Rt△PAQ中,(3﹣x)2=x2+12,
解得x= ( http: / / www.21cnjy.com ),
∴AQ= ( http: / / www.21cnjy.com ).
(2)方法1,如图2,过M作EF⊥CD于F,则EF⊥AB,
∵MD⊥MP,
∴∠PMD=90°,
∴∠PME+∠DMF=90°,
∵∠FDM+∠DMF=90°,
∴∠MDF=∠PME,
∵M是QC的中点,
∴DM= ( http: / / www.21cnjy.com )QC,PM= ( http: / / www.21cnjy.com )QC,
∴DM=PM,
在△MDF和△PME中,
( http: / / www.21cnjy.com ),
∴△MDF≌△PME(AAS),
∴ME=DF,PE=MF,
∵EF⊥CD,AD⊥CD,
∴EF∥AD,
∵QM=MC,
∴DF=CF= ( http: / / www.21cnjy.com )DC= ( http: / / www.21cnjy.com ),
∴ME= ( http: / / www.21cnjy.com ),
∵ME是梯形ABCQ的中位线,
∴2ME=AQ+BC,即5=AQ+3,
∴AQ=2.
( http: / / www.21cnjy.com )
方法2、∵点M是Rt△CDQ的斜边CQ中点,
∴DM=CM,
∴∠DMQ=2∠DCQ,
∵点M是Rt△CPQ的斜边的中点,
∴MP=CM,
∴∠PMQ=2∠PCQ,
∵∠DMP=90°,
∴2∠DCQ+2∠PCQ=90°,
∴∠PCD=45°,°∠BCP=90°﹣45°=45°,
∴∠BPC=45°=∠BCP,∴BP=BC=3,
∵∠CPQ=90°,
∴∠APQ=180°﹣90°﹣45°=45°,
∴∠AQP=90°﹣45°=45°=∠APQ,
∴AQ=AP=2.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
