第19章 矩形、菱形与正方形单元检测A卷
文档属性
| 名称 | 第19章 矩形、菱形与正方形单元检测A卷 |

|
|
| 格式 | doc | ||
| 文件大小 | 534.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-24 00:00:00 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
第19章 矩形、菱形与正方形单元检测A卷
班级__________姓名____________总分___________
一.选择题(共10小题)
1.已知菱形的边长为5cm,一条对角线长为8cm,另一条对角线长为( )
A.3cm B.4cm C.6cm D.8cm
2.如图,P是菱形ABCD对角线BD上一点,PE⊥AB于E,PE=4cm,则点P到BC的距离是( )
( http: / / www.21cnjy.com / )
A.2cm B.3cm C.4cm D.8cm
3.在菱形ABCD中,∠ABC=60°,AB=1,E为边BC的中点.则对角线BD上的动点P到E、C两点的距离之和的最小值为( )2·1·c·n·j·y
A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / ) C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
4.如图,O是正方形ABCD的两条对角线BD,AC的交点,EF过点D,若图中阴影部分的面积为1,则正方形ABCD的周长为( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
A.2 B.4 ( http: / / www.21cnjy.com / ) C.8 D.4
5.如图,在矩形ABCD中,O是对角线AC、BD的交点,点E、F分别是OD、OC的中点.如果AC=10,BC=8,那么EF的长为( )【版权所有:21教育】
( http: / / www.21cnjy.com / )
A.6 B.5 C.4 D.3
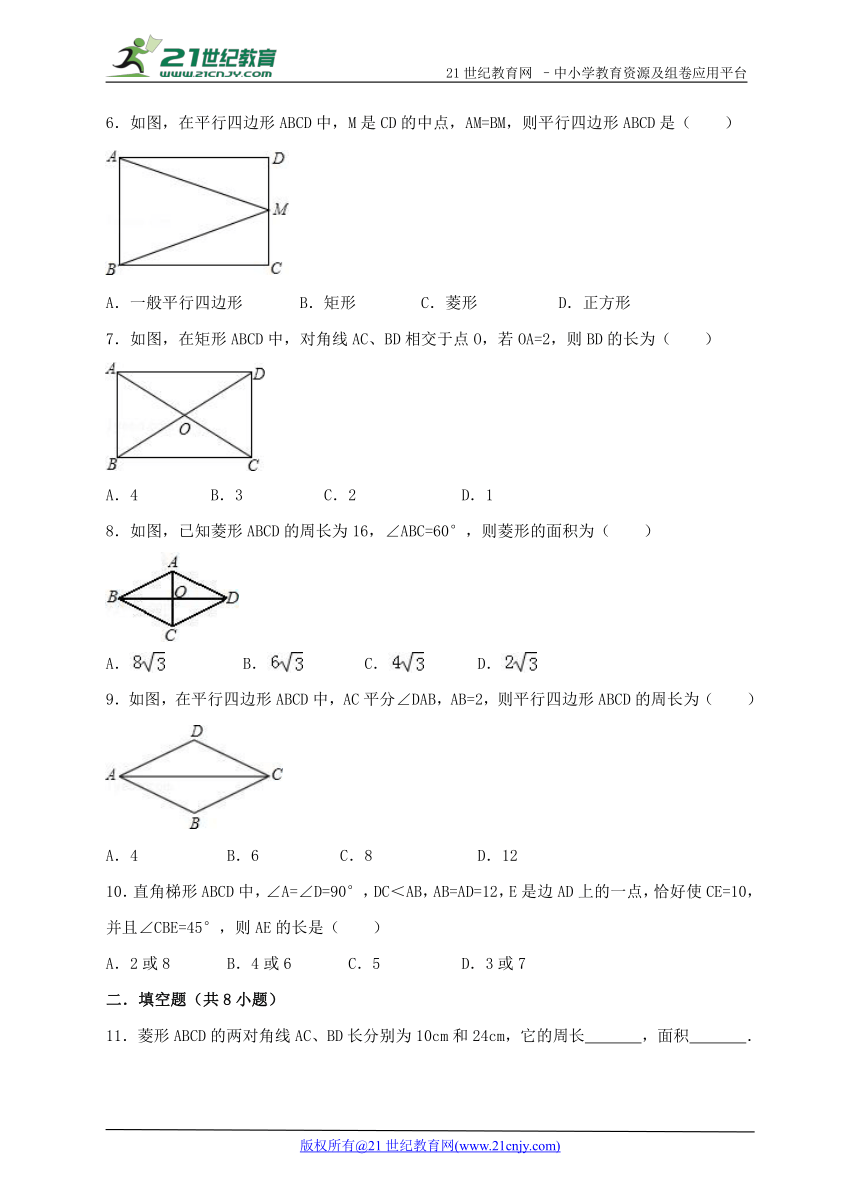
6.如图,在平行四边形ABCD中,M是CD的中点,AM=BM,则平行四边形ABCD是( )
( http: / / www.21cnjy.com / )
A.一般平行四边形 B.矩形 C.菱形 D.正方形
7.如图,在矩形ABCD中,对角线AC、BD相交于点O,若OA=2,则BD的长为( )
( http: / / www.21cnjy.com / )
A.4 B.3 C.2 D.1
8.如图,已知菱形ABCD的周长为16,∠ABC=60°,则菱形的面积为( )
( http: / / www.21cnjy.com / )
A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / ) C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
9.如图,在平行四边形ABCD中,AC平分∠DAB,AB=2,则平行四边形ABCD的周长为( )
( http: / / www.21cnjy.com / )
A.4 B.6 C.8 D.12
10.直角梯形ABCD中,∠A=∠D=9 ( http: / / www.21cnjy.com )0°,DC<AB,AB=AD=12,E是边AD上的一点,恰好使CE=10,并且∠CBE=45°,则AE的长是( )2-1-c-n-j-y
A.2或8 B.4或6 C.5 D.3或7
二.填空题(共8小题)
11.菱形ABCD的两对角线AC、BD长分别为10cm和24cm,它的周长 ,面积 .
( http: / / www.21cnjy.com / )
12.如图,在菱形ABCD中,点E、F分别是BD、CD的中点,EF=6cm,则AB= cm.
( http: / / www.21cnjy.com / )
13.如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=6,则AC= .
( http: / / www.21cnjy.com / )
14.如图,矩形ABCD的对角线相交于O,要使它成为正方形,应添加的条件是 (只填写一个条件即可)21教育网
( http: / / www.21cnjy.com / )
15.如图,BD为长方形ABCD的对角线,BD=10,∠ABD=30°,求长方形ABCD的面积 .
( http: / / www.21cnjy.com / )
16.如图,在正方形ABCD内作一个等边△BEC,连接AE、DE,则∠BEA= .
( http: / / www.21cnjy.com / )
17.如图,已知矩形ABCD中,对角线AC、BD相交于O,AE⊥BD于E,若AB=6,AD=8,则AE= . ( http: / / www.21cnjy.com / )
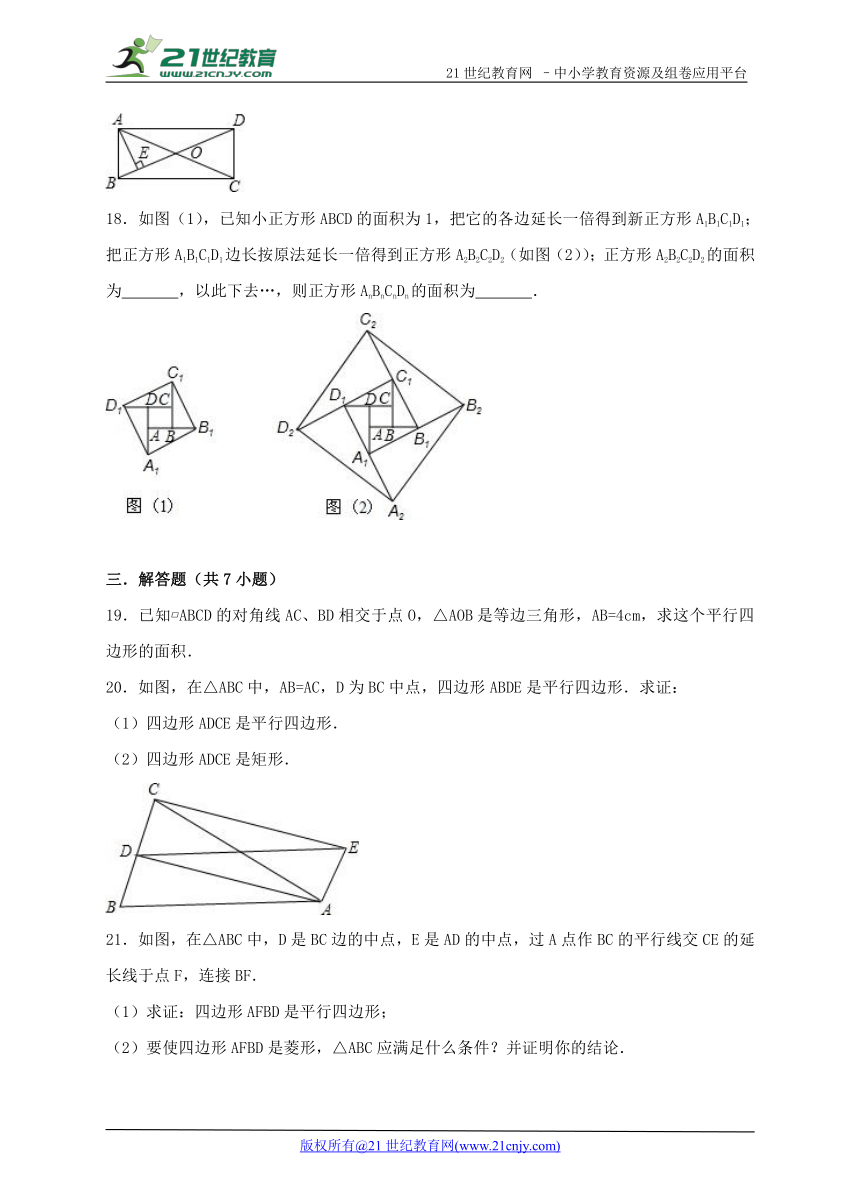
18.如图(1),已知小正方形ABCD的面 ( http: / / www.21cnjy.com )积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2(如图(2));正方形A2B2C2D2的面积为 ,以此下去…,则正方形AnBnCnDn的面积为 .
( http: / / www.21cnjy.com / )
三.解答题(共7小题)
19.已知 ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4cm,求这个平行四边形的面积.21·cn·jy·com
20.如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形.求证:
(1)四边形ADCE是平行四边形.
(2)四边形ADCE是矩形.
( http: / / www.21cnjy.com / )
21.如图,在△ABC中,D是BC边的中点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,连接BF.
(1)求证:四边形AFBD是平行四边形;
(2)要使四边形AFBD是菱形,△ABC应满足什么条件?并证明你的结论.
( http: / / www.21cnjy.com / )
22.Rt△ABC中,CD是斜边AB上的高,BE平分∠CBA交AC于E,交CD于F,CG⊥BE交AB于G.
(1)求证:四边形CFGE是菱形;
(2)若AG=4,BG=6,求AE和DF的长.
( http: / / www.21cnjy.com / )
23.如图,菱形ABCD中,E,F分别是BC,CD上的点,且CE=CF.
(1)求证:△ABE≌△ADF;
(2)过点C作CG∥EA,交AF于点H,交AD于点G,若∠BAE=25°,∠BCD=130°,求∠AHC的度数.
( http: / / www.21cnjy.com / )
24.如图,Rt△ABC中,∠ACB=90°,AC边上的垂直平分线交AC于D,交AB于E,延长DE到F,使BF=CE
(1)四边形BCEF是平行四边形吗?说说你的理由.
(2)当∠A等于多少时,四边形BCEF是菱形,并说出你的理由.
(3)四边形BCEF可以是正方形吗?为什么?
( http: / / www.21cnjy.com / )
25.已知△ABC,DE∥AC交AB于E,DF∥AB交AC于F.
(1)四边形AEDF是什么四边形?
(2)当△ABC满足什么条件时,四边形AEDF是矩形?
(3)当线段AD满足什么条件时,四边形AEDF是菱形?
(4)当△ABC满足什么条件时,四边形AEDF是正方形?
( http: / / www.21cnjy.com / )
参考答案与试题解析
一.选择题(共10小题)
1.
【分析】根据菱形的对角线互相垂直平分,得已知对角线的一半是4cm.根据勾股定理,得要求的对角线的一半是3cm,则另一条对角线的长是6cm.
解:如图:
在菱形ABCD中,AB=5cm,BD=8cm,
∵对角线互相垂直平分,
∴∠AOB=90°,BO=4cm,
在RT△AOB中,AO= ( http: / / www.21cnjy.com / )=3cm,
∴AC=2AO=6cm.
故选:C.
( http: / / www.21cnjy.com / )
2.
【分析】作PF⊥BC于F,如图,根据菱形的性质得BD平分∠ABC,然后根据角平分线的性质易得PF=PE=4cm.
解:作PF⊥BC于F,如图,
∵四边形ABCD为菱形,
∴BD平分∠ABC,
∵PE⊥AB,PF⊥BC,
∴PF=PE=4cm,
即点P到BC的距离为4cm.
故选:C.
( http: / / www.21cnjy.com / )
3.
【分析】连接AC、AE,AE交BD于P,则 ( http: / / www.21cnjy.com )此时PE+PC最小,连接CP,根据菱形的性质得出OA=0C,AC⊥BD,AB=BC,得到A和C关于BD对称,由∠ABC=60°,得出等边三角形ACB,推出AC=AB,根据等腰三角形的性质推出AE⊥BC,推出∠BAE=30°,求出BE和AE长,即可求出答案.
解:连接AC、AE,AE交BD于P,则此时PE+PC最小,连接CP,
∵菱形ABCD,
∴OA=0C,AC⊥BD,AB=BC,
A和C关于BD对称,
∴AP=CP,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=1,
∵E为边BC的中点,
∴AE⊥BC,
∴∠BAE=30°,
∴BE= ( http: / / www.21cnjy.com / ),
根据勾股定理得:AE= ( http: / / www.21cnjy.com / ),
∴PE+PC=AE= ( http: / / www.21cnjy.com / ).
故选:C.
( http: / / www.21cnjy.com / )
4.
【分析】设正方形边长为a,由△AOF≌△COE,可知阴影面积等于△DOC的面积,进而求出边长a.
解:设正方形边长为a,
由题意可知,AO=OC,
∠FAO=∠OCE,∠AOF=∠COE,
∴△AOF≌△COE,
∴知阴影面积等于△DOC的面积,
∴ ( http: / / www.21cnjy.com / )× ( http: / / www.21cnjy.com / )a2=1,
a=2,
∴正方形ABCD的周长为8,
故选:C.
5.
【分析】根据矩形的性质推出AB=CD,∠ABC=90°,根据勾股定理求出AB,即得出CD的长度,根据三角形的中位线定理得出EF= ( http: / / www.21cnjy.com / )CD,即可求出答案.21·世纪*教育网
解:∵四边形ABCD是矩形,
∴AB=CD,∠ABC=90°,
∵AC=10,BC=8,
由勾股定理得:AB= ( http: / / www.21cnjy.com / )=6,
∴CD=AB=6,
∵点E、F分别是OD、OC的中点,
∴EF= ( http: / / www.21cnjy.com / )CD=3.
故选:D.
6.
【分析】首先利用平行四边形 ( http: / / www.21cnjy.com )的性质,得出AD=BC,AD∥BC,以及M是CD的中点,AM=BM,证得△ADM≌△BCM;得出∠ADM=∠BCM,进一步得出∠ADM=∠BCM是直角,证明平行四边形ABCD是矩形.www-2-1-cnjy-com
解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵M是CD的中点,
∴CM=DM,
在△ADM和△BCM中,
( http: / / www.21cnjy.com / ),
∴△ADM≌△BCM(SSS);
∴∠ADM=∠BCM,
∵AD∥BC,
∴∠ADM+∠BCM=180°,
∴∠ADM=∠BCM=90°,
∴平行四边形ABCD是矩形.
故选:B.
7.
【分析】因为矩形的对角线相等且互相平分,已知OA=2,则AC=2OA=4,又BD=AC,故可求.
解:∵ABCD是矩形
∴OC=OA,BD=AC
又∵OA=2,∴AC=OA+OC=2OA=4
∴BD=AC=4
故选:A.
8.
【分析】根据已知求得菱形有边长,再根据勾股定理求得其两条对角线的长,从而就求得了菱形的面积.
解:由题意得,菱形的边长为4,△ABC为等边三角形,得到AC=AD=4,根据勾股定理可求得BD=4 ( http: / / www.21cnjy.com / ),【来源:21cnj*y.co*m】
∴菱形的面积= ( http: / / www.21cnjy.com / )×4×4 ( http: / / www.21cnjy.com / )=8 ( http: / / www.21cnjy.com / ),故选A.
9.
【分析】在平行四边形ABCD中,AC平 ( http: / / www.21cnjy.com )分∠DAB,利用平行线的性质可证△ACD,△ABC为等腰三角形,又AB=CD,则四边形ABCD为菱形,根据菱形的性质求周长.
解:∵四边形ABCD为平行四边形,
∴∠1=∠4,∠2=∠3,
∵AC平分∠DAB,
∴∠1=∠2,
∴∠1=∠3,
∴AD=DC,
四边形ABCD为菱形,
∴四边形ABCD的周长=4×2=8.
故选:C.
( http: / / www.21cnjy.com / )
10.
【分析】过点B作BF⊥CD交DC的 ( http: / / www.21cnjy.com )延长线于F,可得四边形ABFD是正方形,把△ABE绕点B顺时针旋转90°得到△BFG,根据旋转的性质可得AE=FG,BE=BG,∠ABE=∠FBG,然后求出∠CBG=45°,从而得到∠CBE=∠CBG,再利用“边角边”证明△CBE和△CBG全等,根据全等三角形对应边相等可得CE=CG,然后求出AE+CF=CE,设AE=x,表示出DE,再表示出CF、DC,然后在Rt△CDE中,利用勾股定理列出方程求解即可得到AE的长度.
解:如图,过点B作BF⊥CD交DC的延长线于F,
∵∠A=∠D=90°,AB=AD,
∴四边形ABFD是正方形,
把△ABE绕点B顺时针旋转90°得到△BFG,
则AE=FG,BE=BG,∠ABE=∠FBG,
∵∠CBE=45°,
∴∠CBG=∠CBF+∠FBG=∠CBF+∠ABE=90°﹣∠CBE=90°﹣45°=45°,
∴∠CBE=∠CBG,
在△CBE和△CBG中,
( http: / / www.21cnjy.com / ),
∴△CBE≌△CBG(SAS),
∴CE=CG,
∴AE+CF=FG+CF=CG=CE,
设AE=x,则DE=12﹣x,CF=10﹣x,
∴CD=12﹣(10﹣x)=x+2,
在Rt△CDE中,CD2+DE2=CE2,
即(x+2)2+(12﹣x)2=102,
整理得,x2﹣10x+24=0,
解得x1=4,x2=6,
所以AE的长是4或6.
故选:B.
( http: / / www.21cnjy.com / )
二.填空题(共8小题)
11.
【分析】由菱形对角线的性质,相互垂直平分即可得出菱形的边长,菱形四边相等即可得出周长,由菱形面积公式即可求得面积.21教育名师原创作品
解:∵四边形BCD是菱形,
∴AO= ( http: / / www.21cnjy.com / )AC=5cm,BO= ( http: / / www.21cnjy.com / )BD=12cm,且AO⊥BO,
∴AB=13,
∴周长L=4AB=52cm,
∵菱形对角线相互垂直,
∴菱形面积是S= ( http: / / www.21cnjy.com / )AC×BD=120cm2,
故答案为:52cm,120cm2.
12.
【分析】连接AC,得出∠DEC=90°,根据直角三角形斜边上中线性质得出EF= ( http: / / www.21cnjy.com / )CD,求出CD即可.21*cnjy*com
解: ( http: / / www.21cnjy.com / )
连接AC,
∵四边形ABCD是菱形,
∴AB=CD,AC⊥BD,
∴∠DEC=90°,
∵F为CD的中点,
∴EF= ( http: / / www.21cnjy.com / )CD=6,
∴CD=12,
∴AB=CD=12,
故答案为:12.
13.
【分析】根据矩形对角线的性质可推出△ABO为等边三角形.已知AB=6,易求AC.
解:已知∠AOB=60°,根据矩形的性质可得AO=BO,
所以∠OAB=∠ABO=60度.
因为AB=6,所以AO=BO=AB=6.
故AC=12.
14.
【分析】此题是一道开放型的题目答案不唯一,也可以添加AC⊥BD等.
解:AB=BC,
理由是:∵四边形ABCD是矩形,AB=BC,
∴四边形ABCD是正方形,
故答案为:AB=BC.
15.
【分析】长方形各内角为直角,根据B ( http: / / www.21cnjy.com )D=10,∠ABD=30°即可计算AD的长度,根据勾股定理即可计算AB的长,根据长方形面积计算公式即可计算长方形ABCD的面积.
解:长方形各内角为直角,
∴△ABD为直角三角形,
∵BD=10,∠ABD=30°
∴AD=5,
∴AB= ( http: / / www.21cnjy.com / )=5 ( http: / / www.21cnjy.com / ),
∴长方形ABCD的面积为5×5 ( http: / / www.21cnjy.com / )=25 ( http: / / www.21cnjy.com / ).
故答案为 25 ( http: / / www.21cnjy.com / ).
16.
【分析】正方形ABCD中,BC=AB,等边△ ( http: / / www.21cnjy.com )BCE中,BE=AB,即可得AB=BE,因为∠ABE=30°,利用三角形的内角和为180°即可求出∠BEA的度数.21cnjy.com
解:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵△BEC是等边三角形,
∴BC=BE=CE,∠EBC=60°,
∴AB=BE,∠ABE=30°,
∴∠BEA= ( http: / / www.21cnjy.com / )=75°,
故答案为:75°.
17.
【分析】矩形各内角为直角,在直角△ABD中,已知AB、AD,根据勾股定理即可求BD的值,根据面积法即可计算AE的长.
解:矩形各内角为直角,∴△ABD为直角三角形
在直角△ABD中,AB=6,AD=8
则BD= ( http: / / www.21cnjy.com / )=10,
∵△ABD的面积S= ( http: / / www.21cnjy.com / )AB AD= ( http: / / www.21cnjy.com / )BD AE,
∴AE= ( http: / / www.21cnjy.com / )=4.8.
故答案为 4.8.
18.
【分析】根据三角形的面积公 ( http: / / www.21cnjy.com )式,知每一次延长一倍后,得到的一个直角三角形的面积和延长前的正方形的面积相等,即每一次延长一倍后,得到的图形是延长前的正方形的面积的5倍,从而解答.
解:如图(1),已知小正 ( http: / / www.21cnjy.com )方形ABCD的面积为1,则把它的各边延长一倍后,三角形AA1B1的面积是1,新正方形A1B1C1D1的面积是5,从而正方形A2B2C2D2的面积为5×5=25,正方形AnBnCnDn的面积为5n.
故答案为:25,5n.
三.解答题(共7小题)
19.
【分析】根据平行四边形性质得出AO=OC= ( http: / / www.21cnjy.com / )AC,BO=OD= ( http: / / www.21cnjy.com / )BD,根据等边三角形的性质得出AO=BO.推出AC=BD.得出矩形ABCD,根据勾股定理求出BC,即可求出矩形的面积.
解:∵四边形ABCD是平行四边形,
∴AO=OC= ( http: / / www.21cnjy.com / )AC,BO=OD= ( http: / / www.21cnjy.com / )BD,
∵△AOB是等边三角形,
∴AO=BO.
∴AC=BD.
∴平行四边形ABCD是矩形,
在Rt△ABC中,
∵AB=4cm,AC=2AO=8cm,
∴BC= ( http: / / www.21cnjy.com / )=4 ( http: / / www.21cnjy.com / )cm,
∴S平行四边形ABCD=AB×BC=4cm×4 ( http: / / www.21cnjy.com / )cm=16 ( http: / / www.21cnjy.com / )cm2.
( http: / / www.21cnjy.com / )
20.
【分析】(1)根据平行四边形性质得出BD∥AE,BD=AE,推出CD=AE,根据平行四边形的判定推出即可;21世纪教育网版权所有
(2)根据等腰三角形性质求出∠ADC=90°,根据矩形的判定推出即可.
(1)证明:∵四边形ABDE是平行四边形,
∴BD∥AE,BD=AE,
∵D为BC中点,
∴BD=DC,
∴CD∥AE,CD=AE,
∴四边形ADCE是平行四边形;
(2)证明:∵AB=AC,D为BC中点,
∴AD⊥BC,
∴∠ADC=90°,
∵四边形ADCE是平行四边形,
∴平行四边形ADCE是矩形.
21.
【分析】(1)求出AE=DE,∠AFE ( http: / / www.21cnjy.com )=∠DCE,证△AEF≌△CED,推出AF=DC,得出AF∥BD,AF=BD,根据平行四边形的判定推出即可【出处:21教育名师】
(2)当∠BAC=90°时,四边形AFBD是菱形,求出AD=BD即可.
(1)证明:∵E为AD中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DCE,
在△AEF和△CED中,
( http: / / www.21cnjy.com / ),
∴△AEF≌△CED(AAS),
∴AF=DC,
∵AD是△ABC的中线,
∴BD=DC,
∴AF=BD,
即AF∥BD,AF=BD,
故四边形AFBD是平行四边形.
(2)当∠BAC=90°时,四边形AFBD是菱形,
证明:∵∠BAC=90°,D为BC中点,
∴AD=BD,
∵四边形AFBD是平行四边形,
∴四边形AFBD是菱形.
22.
【分析】(1)先证明△BMG≌△BMC ( http: / / www.21cnjy.com ),得出MC=MG,再由线段垂直平分线性质证出EC=EG,FG=FC,然后证明EC=FC,即可证出结论;
(2)先求出BC=BG=6,再求出AC=8,然后证明△AEG∽△ABC,得出比例式 ( http: / / www.21cnjy.com / ),求出AE=5,EC=CF=3,最后根据面积公式得到 ( http: / / www.21cnjy.com / )AB CD= ( http: / / www.21cnjy.com / )AC BC,求出CD= ( http: / / www.21cnjy.com / )=4.8.即可得出DF=CD﹣CF.www.21-cn-jy.com
解:(1)证明:设BE交CG于M.如图所示:
∵BE是∠CBA的平分线,
∴∠1=∠2,
∵CG⊥BE,
∴∠3=∠4=90°,
在△BMG和△BMC中,
( http: / / www.21cnjy.com / ),
∴△BMG≌△BMC(ASA),
∴MC=MG,
∴EC=EG,FG=FC,
∵CD⊥AB,
∴∠DFB+∠1=90°,
∵∠CEF+∠2=90°,∠CFE=∠DFB,
∴∠CEF=∠CFE,
∴EC=FC,
∴EC=EG=FG=FC,
∴四边形CFGE是菱形;
(2)根据题意得:△BEG≌△BEC,
∴BC=BG=6,∠BGE=∠BCA=90°,
∵AB=AG+BG=10,
∴AC= ( http: / / www.21cnjy.com / ),
∵∠A=∠A,∠ABG=∠BCA=90°,
∴△AEG∽△ABC,
∴ ( http: / / www.21cnjy.com / ),即 ( http: / / www.21cnjy.com / ),
∴AE=5.
∴EC=AC﹣AE=3,
∴CF=3,
∵ ( http: / / www.21cnjy.com / )AB CD= ( http: / / www.21cnjy.com / )AC BC,
∴CD= ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / )=4.8,
∴DF=CD﹣CF=4.8﹣3=1.8.
( http: / / www.21cnjy.com / )
23.
【分析】(1)首先利用菱形的性质和CE=CF得出BE=DF,进而得出△ABE≌△ADF;
(2)利用全等三角形的性质得出∠BAE=∠DAF=25°,进而得出∠EAF的度数,进而得出∠AHC的度数.21*cnjy*com
(1)证明:在菱形ABCD中,BC=CD=AB=AD,∠B=∠D(菱形的性质),
∵CE=CF,
∴BC﹣CE=CD﹣CF,
∴BE=DF,
在△ABE与△ADF中
( http: / / www.21cnjy.com / ),
∴△ABE≌△ADF(SAS);
(2)解:∵△ABE≌△ADF(已证),∠BAE=25°,
∴∠BAE=∠DAF=25°,
在菱形ABCD中
∠BAD=∠BCD=130°(菱形对角相等),
∴∠EAF=∠BAD﹣∠BAE﹣∠DAF,
=130°﹣25°﹣25°,
=80°,
∵AE∥CG,
∴∠EAF+∠AHC=180°,
∴∠AHC=180°﹣∠EAF=180°﹣80°=100°.
24.
【分析】(1)四边形BCEF是平行四边形,要证明四边形BCEF是平行四边形可转化为证明FB=CE,FB∥CE即可;
(2)当∠A=30°时,四边形BCEF是菱形,由(1)可知四边形BCEF为平行四边形,只要证明邻边相等即可即证明BC=CE;
(3)不可以,因为∠BCE始终是锐角,所以四边形BCEF不可能是正方形.
(1)四边形BCEF是平行四边形,理由如下:
证明:∵DF垂直且平分AC且∠ACB=90°
∴FD∥BC,AE=CE,
∴∠A=∠ACE,
∵∠A+∠ABC=∠ACE+∠BCE=90°,
∴∠ABC=∠BCE,
∴BE=CE=BF,
∴∠BFE=∠BEF
∵FD∥BC,
∴∠BFE=∠BEF=∠ABC=∠BCE
∴∠FBE=∠BEC,
∴FB∥EC,
∵CE=BF,
∴四边形BCEF为平行四边形;
(2)∠A=30°,
证明:∵∠A=30°,
∴∠ABC=60°且BE=CE,
∴△BCE为等边三角形,
∴BC=CE,
由(1)可知四边形BCEF为平行四边形,
∴四边形BCEF为菱形;
(3)不可以,
因为∠BCE始终是锐角,所以四边形BCEF不可能是正方形.
25.
【分析】(1)根据平行四边形的对边平行的判定方法即可判定;
(2)根据矩形的定义即可解题;
(3)根据菱形对角线互相垂直即可解题;
(4)根据正方形即使菱形又是矩形即可解本题.
解:(1)∵DE∥AC,DF∥AB
∴四边形AEDF是平行四边形;
(2)∵一个角为直角的平行四边形为矩形,
∴∠BAC=90°时,四边形AEDF是矩形;
(3)∵菱形对角线互相垂直,
∴当AD⊥EF时,四边形AEDF是菱形;
(4)∵正方形既是菱形又是矩形,
∴∠BAC=90°且AD⊥BC时,四边形AEDF是正方形.
( http: / / www.21cnjy.com / )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
第19章 矩形、菱形与正方形单元检测A卷
班级__________姓名____________总分___________
一.选择题(共10小题)
1.已知菱形的边长为5cm,一条对角线长为8cm,另一条对角线长为( )
A.3cm B.4cm C.6cm D.8cm
2.如图,P是菱形ABCD对角线BD上一点,PE⊥AB于E,PE=4cm,则点P到BC的距离是( )
( http: / / www.21cnjy.com / )
A.2cm B.3cm C.4cm D.8cm
3.在菱形ABCD中,∠ABC=60°,AB=1,E为边BC的中点.则对角线BD上的动点P到E、C两点的距离之和的最小值为( )2·1·c·n·j·y
A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / ) C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
4.如图,O是正方形ABCD的两条对角线BD,AC的交点,EF过点D,若图中阴影部分的面积为1,则正方形ABCD的周长为( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
A.2 B.4 ( http: / / www.21cnjy.com / ) C.8 D.4
5.如图,在矩形ABCD中,O是对角线AC、BD的交点,点E、F分别是OD、OC的中点.如果AC=10,BC=8,那么EF的长为( )【版权所有:21教育】
( http: / / www.21cnjy.com / )
A.6 B.5 C.4 D.3
6.如图,在平行四边形ABCD中,M是CD的中点,AM=BM,则平行四边形ABCD是( )
( http: / / www.21cnjy.com / )
A.一般平行四边形 B.矩形 C.菱形 D.正方形
7.如图,在矩形ABCD中,对角线AC、BD相交于点O,若OA=2,则BD的长为( )
( http: / / www.21cnjy.com / )
A.4 B.3 C.2 D.1
8.如图,已知菱形ABCD的周长为16,∠ABC=60°,则菱形的面积为( )
( http: / / www.21cnjy.com / )
A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / ) C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
9.如图,在平行四边形ABCD中,AC平分∠DAB,AB=2,则平行四边形ABCD的周长为( )
( http: / / www.21cnjy.com / )
A.4 B.6 C.8 D.12
10.直角梯形ABCD中,∠A=∠D=9 ( http: / / www.21cnjy.com )0°,DC<AB,AB=AD=12,E是边AD上的一点,恰好使CE=10,并且∠CBE=45°,则AE的长是( )2-1-c-n-j-y
A.2或8 B.4或6 C.5 D.3或7
二.填空题(共8小题)
11.菱形ABCD的两对角线AC、BD长分别为10cm和24cm,它的周长 ,面积 .
( http: / / www.21cnjy.com / )
12.如图,在菱形ABCD中,点E、F分别是BD、CD的中点,EF=6cm,则AB= cm.
( http: / / www.21cnjy.com / )
13.如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=6,则AC= .
( http: / / www.21cnjy.com / )
14.如图,矩形ABCD的对角线相交于O,要使它成为正方形,应添加的条件是 (只填写一个条件即可)21教育网
( http: / / www.21cnjy.com / )
15.如图,BD为长方形ABCD的对角线,BD=10,∠ABD=30°,求长方形ABCD的面积 .
( http: / / www.21cnjy.com / )
16.如图,在正方形ABCD内作一个等边△BEC,连接AE、DE,则∠BEA= .
( http: / / www.21cnjy.com / )
17.如图,已知矩形ABCD中,对角线AC、BD相交于O,AE⊥BD于E,若AB=6,AD=8,则AE= . ( http: / / www.21cnjy.com / )
18.如图(1),已知小正方形ABCD的面 ( http: / / www.21cnjy.com )积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2(如图(2));正方形A2B2C2D2的面积为 ,以此下去…,则正方形AnBnCnDn的面积为 .
( http: / / www.21cnjy.com / )
三.解答题(共7小题)
19.已知 ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4cm,求这个平行四边形的面积.21·cn·jy·com
20.如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形.求证:
(1)四边形ADCE是平行四边形.
(2)四边形ADCE是矩形.
( http: / / www.21cnjy.com / )
21.如图,在△ABC中,D是BC边的中点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,连接BF.
(1)求证:四边形AFBD是平行四边形;
(2)要使四边形AFBD是菱形,△ABC应满足什么条件?并证明你的结论.
( http: / / www.21cnjy.com / )
22.Rt△ABC中,CD是斜边AB上的高,BE平分∠CBA交AC于E,交CD于F,CG⊥BE交AB于G.
(1)求证:四边形CFGE是菱形;
(2)若AG=4,BG=6,求AE和DF的长.
( http: / / www.21cnjy.com / )
23.如图,菱形ABCD中,E,F分别是BC,CD上的点,且CE=CF.
(1)求证:△ABE≌△ADF;
(2)过点C作CG∥EA,交AF于点H,交AD于点G,若∠BAE=25°,∠BCD=130°,求∠AHC的度数.
( http: / / www.21cnjy.com / )
24.如图,Rt△ABC中,∠ACB=90°,AC边上的垂直平分线交AC于D,交AB于E,延长DE到F,使BF=CE
(1)四边形BCEF是平行四边形吗?说说你的理由.
(2)当∠A等于多少时,四边形BCEF是菱形,并说出你的理由.
(3)四边形BCEF可以是正方形吗?为什么?
( http: / / www.21cnjy.com / )
25.已知△ABC,DE∥AC交AB于E,DF∥AB交AC于F.
(1)四边形AEDF是什么四边形?
(2)当△ABC满足什么条件时,四边形AEDF是矩形?
(3)当线段AD满足什么条件时,四边形AEDF是菱形?
(4)当△ABC满足什么条件时,四边形AEDF是正方形?
( http: / / www.21cnjy.com / )
参考答案与试题解析
一.选择题(共10小题)
1.
【分析】根据菱形的对角线互相垂直平分,得已知对角线的一半是4cm.根据勾股定理,得要求的对角线的一半是3cm,则另一条对角线的长是6cm.
解:如图:
在菱形ABCD中,AB=5cm,BD=8cm,
∵对角线互相垂直平分,
∴∠AOB=90°,BO=4cm,
在RT△AOB中,AO= ( http: / / www.21cnjy.com / )=3cm,
∴AC=2AO=6cm.
故选:C.
( http: / / www.21cnjy.com / )
2.
【分析】作PF⊥BC于F,如图,根据菱形的性质得BD平分∠ABC,然后根据角平分线的性质易得PF=PE=4cm.
解:作PF⊥BC于F,如图,
∵四边形ABCD为菱形,
∴BD平分∠ABC,
∵PE⊥AB,PF⊥BC,
∴PF=PE=4cm,
即点P到BC的距离为4cm.
故选:C.
( http: / / www.21cnjy.com / )
3.
【分析】连接AC、AE,AE交BD于P,则 ( http: / / www.21cnjy.com )此时PE+PC最小,连接CP,根据菱形的性质得出OA=0C,AC⊥BD,AB=BC,得到A和C关于BD对称,由∠ABC=60°,得出等边三角形ACB,推出AC=AB,根据等腰三角形的性质推出AE⊥BC,推出∠BAE=30°,求出BE和AE长,即可求出答案.
解:连接AC、AE,AE交BD于P,则此时PE+PC最小,连接CP,
∵菱形ABCD,
∴OA=0C,AC⊥BD,AB=BC,
A和C关于BD对称,
∴AP=CP,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=1,
∵E为边BC的中点,
∴AE⊥BC,
∴∠BAE=30°,
∴BE= ( http: / / www.21cnjy.com / ),
根据勾股定理得:AE= ( http: / / www.21cnjy.com / ),
∴PE+PC=AE= ( http: / / www.21cnjy.com / ).
故选:C.
( http: / / www.21cnjy.com / )
4.
【分析】设正方形边长为a,由△AOF≌△COE,可知阴影面积等于△DOC的面积,进而求出边长a.
解:设正方形边长为a,
由题意可知,AO=OC,
∠FAO=∠OCE,∠AOF=∠COE,
∴△AOF≌△COE,
∴知阴影面积等于△DOC的面积,
∴ ( http: / / www.21cnjy.com / )× ( http: / / www.21cnjy.com / )a2=1,
a=2,
∴正方形ABCD的周长为8,
故选:C.
5.
【分析】根据矩形的性质推出AB=CD,∠ABC=90°,根据勾股定理求出AB,即得出CD的长度,根据三角形的中位线定理得出EF= ( http: / / www.21cnjy.com / )CD,即可求出答案.21·世纪*教育网
解:∵四边形ABCD是矩形,
∴AB=CD,∠ABC=90°,
∵AC=10,BC=8,
由勾股定理得:AB= ( http: / / www.21cnjy.com / )=6,
∴CD=AB=6,
∵点E、F分别是OD、OC的中点,
∴EF= ( http: / / www.21cnjy.com / )CD=3.
故选:D.
6.
【分析】首先利用平行四边形 ( http: / / www.21cnjy.com )的性质,得出AD=BC,AD∥BC,以及M是CD的中点,AM=BM,证得△ADM≌△BCM;得出∠ADM=∠BCM,进一步得出∠ADM=∠BCM是直角,证明平行四边形ABCD是矩形.www-2-1-cnjy-com
解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵M是CD的中点,
∴CM=DM,
在△ADM和△BCM中,
( http: / / www.21cnjy.com / ),
∴△ADM≌△BCM(SSS);
∴∠ADM=∠BCM,
∵AD∥BC,
∴∠ADM+∠BCM=180°,
∴∠ADM=∠BCM=90°,
∴平行四边形ABCD是矩形.
故选:B.
7.
【分析】因为矩形的对角线相等且互相平分,已知OA=2,则AC=2OA=4,又BD=AC,故可求.
解:∵ABCD是矩形
∴OC=OA,BD=AC
又∵OA=2,∴AC=OA+OC=2OA=4
∴BD=AC=4
故选:A.
8.
【分析】根据已知求得菱形有边长,再根据勾股定理求得其两条对角线的长,从而就求得了菱形的面积.
解:由题意得,菱形的边长为4,△ABC为等边三角形,得到AC=AD=4,根据勾股定理可求得BD=4 ( http: / / www.21cnjy.com / ),【来源:21cnj*y.co*m】
∴菱形的面积= ( http: / / www.21cnjy.com / )×4×4 ( http: / / www.21cnjy.com / )=8 ( http: / / www.21cnjy.com / ),故选A.
9.
【分析】在平行四边形ABCD中,AC平 ( http: / / www.21cnjy.com )分∠DAB,利用平行线的性质可证△ACD,△ABC为等腰三角形,又AB=CD,则四边形ABCD为菱形,根据菱形的性质求周长.
解:∵四边形ABCD为平行四边形,
∴∠1=∠4,∠2=∠3,
∵AC平分∠DAB,
∴∠1=∠2,
∴∠1=∠3,
∴AD=DC,
四边形ABCD为菱形,
∴四边形ABCD的周长=4×2=8.
故选:C.
( http: / / www.21cnjy.com / )
10.
【分析】过点B作BF⊥CD交DC的 ( http: / / www.21cnjy.com )延长线于F,可得四边形ABFD是正方形,把△ABE绕点B顺时针旋转90°得到△BFG,根据旋转的性质可得AE=FG,BE=BG,∠ABE=∠FBG,然后求出∠CBG=45°,从而得到∠CBE=∠CBG,再利用“边角边”证明△CBE和△CBG全等,根据全等三角形对应边相等可得CE=CG,然后求出AE+CF=CE,设AE=x,表示出DE,再表示出CF、DC,然后在Rt△CDE中,利用勾股定理列出方程求解即可得到AE的长度.
解:如图,过点B作BF⊥CD交DC的延长线于F,
∵∠A=∠D=90°,AB=AD,
∴四边形ABFD是正方形,
把△ABE绕点B顺时针旋转90°得到△BFG,
则AE=FG,BE=BG,∠ABE=∠FBG,
∵∠CBE=45°,
∴∠CBG=∠CBF+∠FBG=∠CBF+∠ABE=90°﹣∠CBE=90°﹣45°=45°,
∴∠CBE=∠CBG,
在△CBE和△CBG中,
( http: / / www.21cnjy.com / ),
∴△CBE≌△CBG(SAS),
∴CE=CG,
∴AE+CF=FG+CF=CG=CE,
设AE=x,则DE=12﹣x,CF=10﹣x,
∴CD=12﹣(10﹣x)=x+2,
在Rt△CDE中,CD2+DE2=CE2,
即(x+2)2+(12﹣x)2=102,
整理得,x2﹣10x+24=0,
解得x1=4,x2=6,
所以AE的长是4或6.
故选:B.
( http: / / www.21cnjy.com / )
二.填空题(共8小题)
11.
【分析】由菱形对角线的性质,相互垂直平分即可得出菱形的边长,菱形四边相等即可得出周长,由菱形面积公式即可求得面积.21教育名师原创作品
解:∵四边形BCD是菱形,
∴AO= ( http: / / www.21cnjy.com / )AC=5cm,BO= ( http: / / www.21cnjy.com / )BD=12cm,且AO⊥BO,
∴AB=13,
∴周长L=4AB=52cm,
∵菱形对角线相互垂直,
∴菱形面积是S= ( http: / / www.21cnjy.com / )AC×BD=120cm2,
故答案为:52cm,120cm2.
12.
【分析】连接AC,得出∠DEC=90°,根据直角三角形斜边上中线性质得出EF= ( http: / / www.21cnjy.com / )CD,求出CD即可.21*cnjy*com
解: ( http: / / www.21cnjy.com / )
连接AC,
∵四边形ABCD是菱形,
∴AB=CD,AC⊥BD,
∴∠DEC=90°,
∵F为CD的中点,
∴EF= ( http: / / www.21cnjy.com / )CD=6,
∴CD=12,
∴AB=CD=12,
故答案为:12.
13.
【分析】根据矩形对角线的性质可推出△ABO为等边三角形.已知AB=6,易求AC.
解:已知∠AOB=60°,根据矩形的性质可得AO=BO,
所以∠OAB=∠ABO=60度.
因为AB=6,所以AO=BO=AB=6.
故AC=12.
14.
【分析】此题是一道开放型的题目答案不唯一,也可以添加AC⊥BD等.
解:AB=BC,
理由是:∵四边形ABCD是矩形,AB=BC,
∴四边形ABCD是正方形,
故答案为:AB=BC.
15.
【分析】长方形各内角为直角,根据B ( http: / / www.21cnjy.com )D=10,∠ABD=30°即可计算AD的长度,根据勾股定理即可计算AB的长,根据长方形面积计算公式即可计算长方形ABCD的面积.
解:长方形各内角为直角,
∴△ABD为直角三角形,
∵BD=10,∠ABD=30°
∴AD=5,
∴AB= ( http: / / www.21cnjy.com / )=5 ( http: / / www.21cnjy.com / ),
∴长方形ABCD的面积为5×5 ( http: / / www.21cnjy.com / )=25 ( http: / / www.21cnjy.com / ).
故答案为 25 ( http: / / www.21cnjy.com / ).
16.
【分析】正方形ABCD中,BC=AB,等边△ ( http: / / www.21cnjy.com )BCE中,BE=AB,即可得AB=BE,因为∠ABE=30°,利用三角形的内角和为180°即可求出∠BEA的度数.21cnjy.com
解:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵△BEC是等边三角形,
∴BC=BE=CE,∠EBC=60°,
∴AB=BE,∠ABE=30°,
∴∠BEA= ( http: / / www.21cnjy.com / )=75°,
故答案为:75°.
17.
【分析】矩形各内角为直角,在直角△ABD中,已知AB、AD,根据勾股定理即可求BD的值,根据面积法即可计算AE的长.
解:矩形各内角为直角,∴△ABD为直角三角形
在直角△ABD中,AB=6,AD=8
则BD= ( http: / / www.21cnjy.com / )=10,
∵△ABD的面积S= ( http: / / www.21cnjy.com / )AB AD= ( http: / / www.21cnjy.com / )BD AE,
∴AE= ( http: / / www.21cnjy.com / )=4.8.
故答案为 4.8.
18.
【分析】根据三角形的面积公 ( http: / / www.21cnjy.com )式,知每一次延长一倍后,得到的一个直角三角形的面积和延长前的正方形的面积相等,即每一次延长一倍后,得到的图形是延长前的正方形的面积的5倍,从而解答.
解:如图(1),已知小正 ( http: / / www.21cnjy.com )方形ABCD的面积为1,则把它的各边延长一倍后,三角形AA1B1的面积是1,新正方形A1B1C1D1的面积是5,从而正方形A2B2C2D2的面积为5×5=25,正方形AnBnCnDn的面积为5n.
故答案为:25,5n.
三.解答题(共7小题)
19.
【分析】根据平行四边形性质得出AO=OC= ( http: / / www.21cnjy.com / )AC,BO=OD= ( http: / / www.21cnjy.com / )BD,根据等边三角形的性质得出AO=BO.推出AC=BD.得出矩形ABCD,根据勾股定理求出BC,即可求出矩形的面积.
解:∵四边形ABCD是平行四边形,
∴AO=OC= ( http: / / www.21cnjy.com / )AC,BO=OD= ( http: / / www.21cnjy.com / )BD,
∵△AOB是等边三角形,
∴AO=BO.
∴AC=BD.
∴平行四边形ABCD是矩形,
在Rt△ABC中,
∵AB=4cm,AC=2AO=8cm,
∴BC= ( http: / / www.21cnjy.com / )=4 ( http: / / www.21cnjy.com / )cm,
∴S平行四边形ABCD=AB×BC=4cm×4 ( http: / / www.21cnjy.com / )cm=16 ( http: / / www.21cnjy.com / )cm2.
( http: / / www.21cnjy.com / )
20.
【分析】(1)根据平行四边形性质得出BD∥AE,BD=AE,推出CD=AE,根据平行四边形的判定推出即可;21世纪教育网版权所有
(2)根据等腰三角形性质求出∠ADC=90°,根据矩形的判定推出即可.
(1)证明:∵四边形ABDE是平行四边形,
∴BD∥AE,BD=AE,
∵D为BC中点,
∴BD=DC,
∴CD∥AE,CD=AE,
∴四边形ADCE是平行四边形;
(2)证明:∵AB=AC,D为BC中点,
∴AD⊥BC,
∴∠ADC=90°,
∵四边形ADCE是平行四边形,
∴平行四边形ADCE是矩形.
21.
【分析】(1)求出AE=DE,∠AFE ( http: / / www.21cnjy.com )=∠DCE,证△AEF≌△CED,推出AF=DC,得出AF∥BD,AF=BD,根据平行四边形的判定推出即可【出处:21教育名师】
(2)当∠BAC=90°时,四边形AFBD是菱形,求出AD=BD即可.
(1)证明:∵E为AD中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DCE,
在△AEF和△CED中,
( http: / / www.21cnjy.com / ),
∴△AEF≌△CED(AAS),
∴AF=DC,
∵AD是△ABC的中线,
∴BD=DC,
∴AF=BD,
即AF∥BD,AF=BD,
故四边形AFBD是平行四边形.
(2)当∠BAC=90°时,四边形AFBD是菱形,
证明:∵∠BAC=90°,D为BC中点,
∴AD=BD,
∵四边形AFBD是平行四边形,
∴四边形AFBD是菱形.
22.
【分析】(1)先证明△BMG≌△BMC ( http: / / www.21cnjy.com ),得出MC=MG,再由线段垂直平分线性质证出EC=EG,FG=FC,然后证明EC=FC,即可证出结论;
(2)先求出BC=BG=6,再求出AC=8,然后证明△AEG∽△ABC,得出比例式 ( http: / / www.21cnjy.com / ),求出AE=5,EC=CF=3,最后根据面积公式得到 ( http: / / www.21cnjy.com / )AB CD= ( http: / / www.21cnjy.com / )AC BC,求出CD= ( http: / / www.21cnjy.com / )=4.8.即可得出DF=CD﹣CF.www.21-cn-jy.com
解:(1)证明:设BE交CG于M.如图所示:
∵BE是∠CBA的平分线,
∴∠1=∠2,
∵CG⊥BE,
∴∠3=∠4=90°,
在△BMG和△BMC中,
( http: / / www.21cnjy.com / ),
∴△BMG≌△BMC(ASA),
∴MC=MG,
∴EC=EG,FG=FC,
∵CD⊥AB,
∴∠DFB+∠1=90°,
∵∠CEF+∠2=90°,∠CFE=∠DFB,
∴∠CEF=∠CFE,
∴EC=FC,
∴EC=EG=FG=FC,
∴四边形CFGE是菱形;
(2)根据题意得:△BEG≌△BEC,
∴BC=BG=6,∠BGE=∠BCA=90°,
∵AB=AG+BG=10,
∴AC= ( http: / / www.21cnjy.com / ),
∵∠A=∠A,∠ABG=∠BCA=90°,
∴△AEG∽△ABC,
∴ ( http: / / www.21cnjy.com / ),即 ( http: / / www.21cnjy.com / ),
∴AE=5.
∴EC=AC﹣AE=3,
∴CF=3,
∵ ( http: / / www.21cnjy.com / )AB CD= ( http: / / www.21cnjy.com / )AC BC,
∴CD= ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / )=4.8,
∴DF=CD﹣CF=4.8﹣3=1.8.
( http: / / www.21cnjy.com / )
23.
【分析】(1)首先利用菱形的性质和CE=CF得出BE=DF,进而得出△ABE≌△ADF;
(2)利用全等三角形的性质得出∠BAE=∠DAF=25°,进而得出∠EAF的度数,进而得出∠AHC的度数.21*cnjy*com
(1)证明:在菱形ABCD中,BC=CD=AB=AD,∠B=∠D(菱形的性质),
∵CE=CF,
∴BC﹣CE=CD﹣CF,
∴BE=DF,
在△ABE与△ADF中
( http: / / www.21cnjy.com / ),
∴△ABE≌△ADF(SAS);
(2)解:∵△ABE≌△ADF(已证),∠BAE=25°,
∴∠BAE=∠DAF=25°,
在菱形ABCD中
∠BAD=∠BCD=130°(菱形对角相等),
∴∠EAF=∠BAD﹣∠BAE﹣∠DAF,
=130°﹣25°﹣25°,
=80°,
∵AE∥CG,
∴∠EAF+∠AHC=180°,
∴∠AHC=180°﹣∠EAF=180°﹣80°=100°.
24.
【分析】(1)四边形BCEF是平行四边形,要证明四边形BCEF是平行四边形可转化为证明FB=CE,FB∥CE即可;
(2)当∠A=30°时,四边形BCEF是菱形,由(1)可知四边形BCEF为平行四边形,只要证明邻边相等即可即证明BC=CE;
(3)不可以,因为∠BCE始终是锐角,所以四边形BCEF不可能是正方形.
(1)四边形BCEF是平行四边形,理由如下:
证明:∵DF垂直且平分AC且∠ACB=90°
∴FD∥BC,AE=CE,
∴∠A=∠ACE,
∵∠A+∠ABC=∠ACE+∠BCE=90°,
∴∠ABC=∠BCE,
∴BE=CE=BF,
∴∠BFE=∠BEF
∵FD∥BC,
∴∠BFE=∠BEF=∠ABC=∠BCE
∴∠FBE=∠BEC,
∴FB∥EC,
∵CE=BF,
∴四边形BCEF为平行四边形;
(2)∠A=30°,
证明:∵∠A=30°,
∴∠ABC=60°且BE=CE,
∴△BCE为等边三角形,
∴BC=CE,
由(1)可知四边形BCEF为平行四边形,
∴四边形BCEF为菱形;
(3)不可以,
因为∠BCE始终是锐角,所以四边形BCEF不可能是正方形.
25.
【分析】(1)根据平行四边形的对边平行的判定方法即可判定;
(2)根据矩形的定义即可解题;
(3)根据菱形对角线互相垂直即可解题;
(4)根据正方形即使菱形又是矩形即可解本题.
解:(1)∵DE∥AC,DF∥AB
∴四边形AEDF是平行四边形;
(2)∵一个角为直角的平行四边形为矩形,
∴∠BAC=90°时,四边形AEDF是矩形;
(3)∵菱形对角线互相垂直,
∴当AD⊥EF时,四边形AEDF是菱形;
(4)∵正方形既是菱形又是矩形,
∴∠BAC=90°且AD⊥BC时,四边形AEDF是正方形.
( http: / / www.21cnjy.com / )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
