26.3实践与探索课件 (共31张PPT)
文档属性
| 名称 | 26.3实践与探索课件 (共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 430.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-25 23:55:12 | ||
图片预览






文档简介
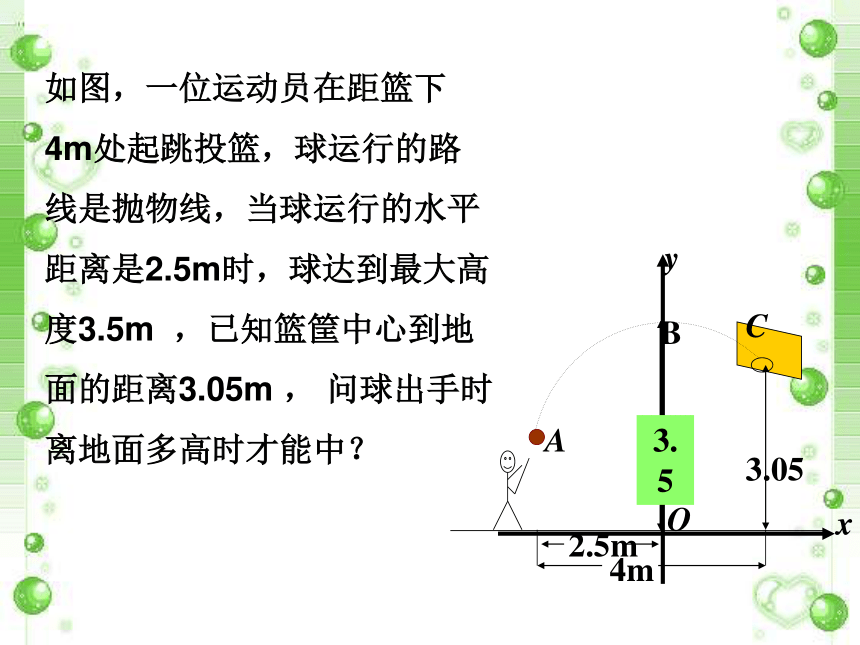
课件31张PPT。 实践与探索如图,一位运动员在距篮下4m处起跳投篮,球运行的路线是抛物线,当球运行的水平距离是2.5m时,球达到最大高度3.5m ,已知篮筐中心到地面的距离3.05m , 问球出手时离地面多高时才能中? 球的出手点A的横坐标为-2.5,将x=-2.5代入抛物线表达式得y=2.25,即当出手高度为2.25m时,才能投中.解:建立如图所示的直角坐标系,则球的最高点和球篮的坐标分别为B(0,3.5),C(1.5,3.05).∴该抛物线的表达式为y=-0.2x2+3.5.市植物园人工湖上有抛物线型拱桥,正常水位时桥下水面宽20米,拱高4米,根据此条件建立如图所示坐标系,得知此时抛物线的解析式为 y= - x2+4
①在正常水位基础上水位上升 h 米时,桥下水面宽为d 米,求d与h 函数关系式.
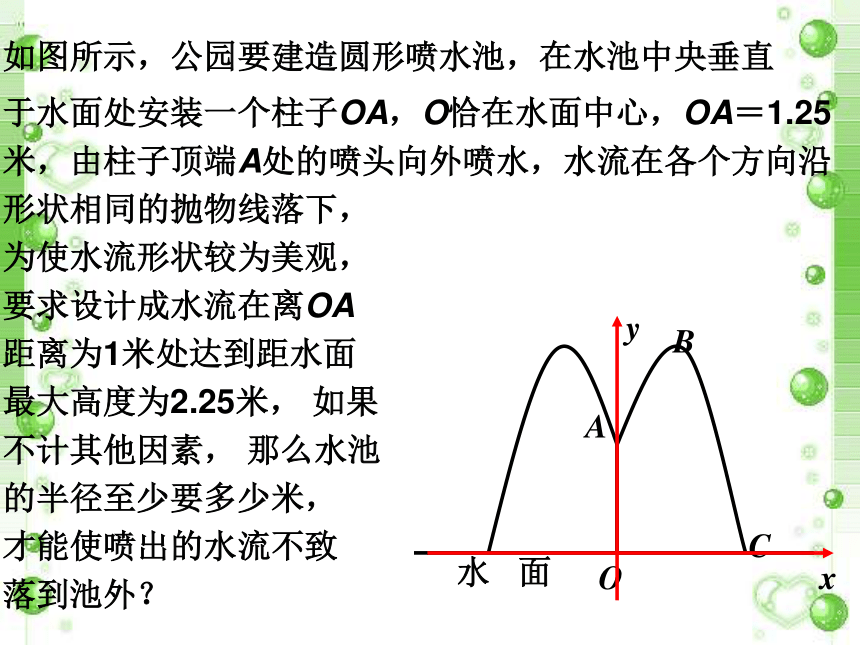
②正常水位时,桥下水深2米,为了保证游船顺利通过,桥下水面宽不得小于18 .求水深超过多少会影响过往游船在桥下顺利航行?如图所示,公园要建造圆形喷水池,在水池中央垂直
于水面处安装一个柱子OA,O恰在水面中心,OA=1.25
米,由柱子顶端A处的喷头向外喷水,水流在各个方向沿
形状相同的抛物线落下,
为使水流形状较为美观,
要求设计成水流在离OA
距离为1米处达到距水面
最大高度为2.25米, 如果
不计其他因素, 那么水池
的半径至少要多少米,
才能使喷出的水流不致
落到池外?
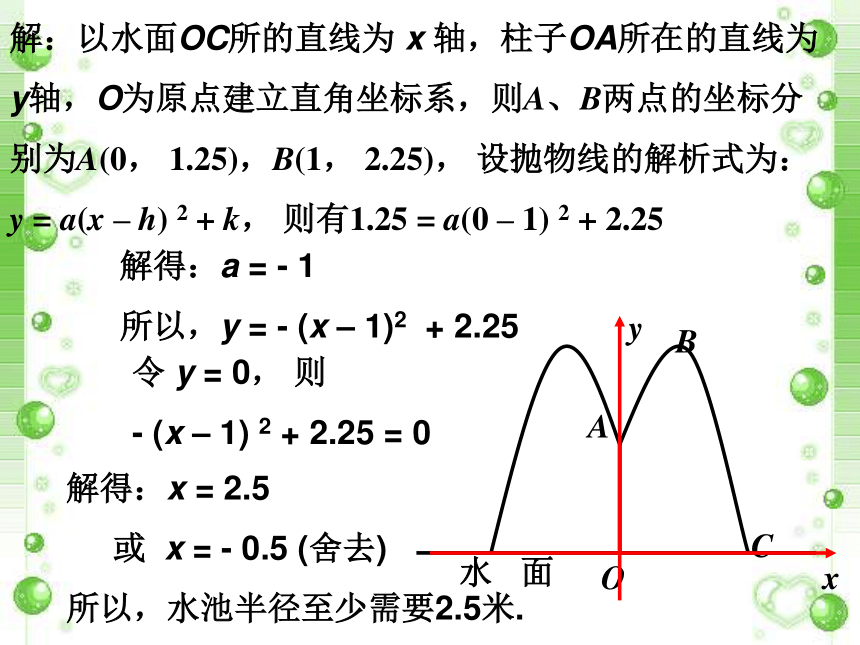
解:以水面OC所的直线为 x 轴,柱子OA所在的直线为y轴,O为原点建立直角坐标系,则A、B两点的坐标分别为A(0, 1.25),B(1, 2.25), 设抛物线的解析式为:y = a(x – h) 2 + k, 则有1.25 = a(0 – 1) 2 + 2.25 解得:a = - 1
所以,y = - (x – 1)2 + 2.25令 y = 0, 则
- (x – 1) 2 + 2.25 = 0解得:x = 2.5
或 x = - 0.5 (舍去)
所以,水池半径至少需要2.5米. 练习1:
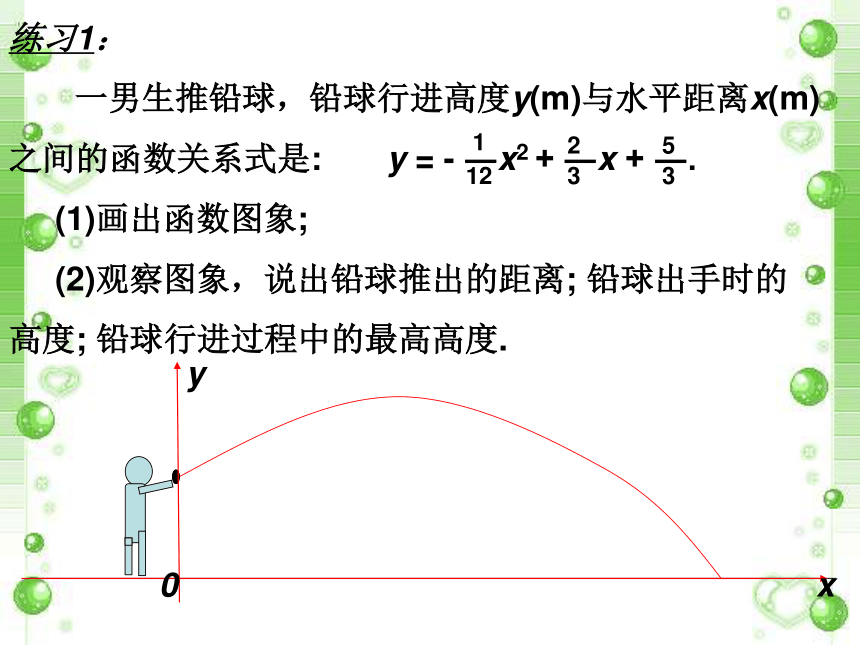
一男生推铅球,铅球行进高度y(m)与水平距离x(m)之间的函数关系式是: y = - ―x2 + ―x + ―.
(1)画出函数图象;
(2)观察图象,说出铅球推出的距离; 铅球出手时的高度; 铅球行进过程中的最高高度.YX练习2:
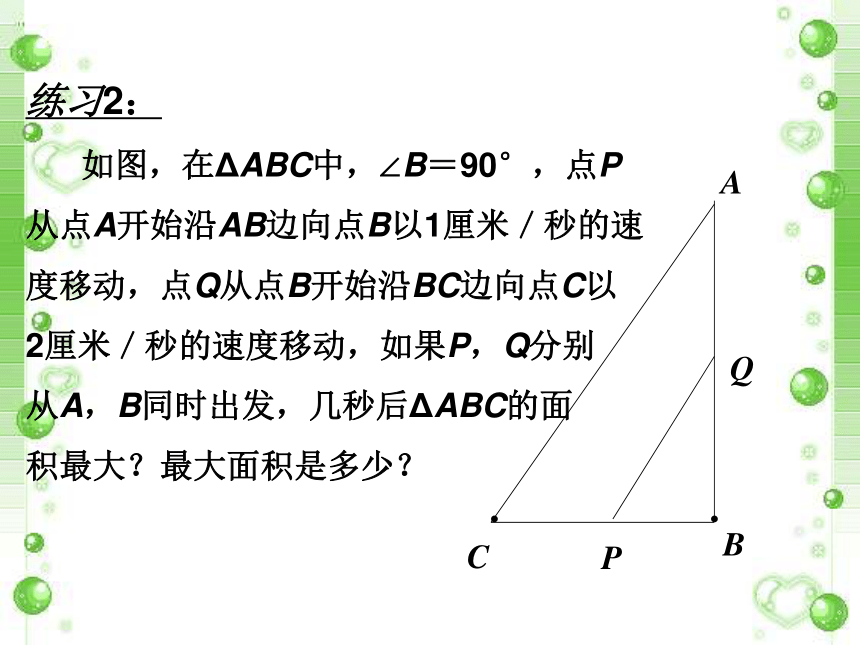
如图,在ΔABC中,∠B=90°,点P
从点A开始沿AB边向点B以1厘米/秒的速
度移动,点Q从点B开始沿BC边向点C以
2厘米/秒的速度移动,如果P,Q分别
从A,B同时出发,几秒后ΔABC的面
积最大?最大面积是多少?PQ强化训练你知道吗,平时我们在跳大绳时,绳甩到最高处的形状可以看为抛物线.如图所示,正在甩绳的甲乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙丁分别站在距甲拿绳的手水平距离1米2.5米处,绳子到最高处时刚好通过他们的头顶.已知学生丙的身高是1.5米,求学生丁的身高?归纳:运用二次函数的性质求实际问题的最大值和最小值的一般步骤 :求出函数解析式和自变量的取值范围配方变形,或利用公式求它的最大值或最小值.检查求得的最大值或最小值对应的字变量的值必须在自变量的取值范围内 . 一个球从地面上竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m).已知物体竖直上抛运动中,h=v0t- gt2(v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s2).问球从弹起至回到地面需要多少时间?经多少时间球的高度达到3.75m?地面解:由题意,得h关于t的二次函数
解析式为h=10t-5t2取h=0,得一元二次方程
10t-5t2=0解方程得t1=0;t2=2球从弹起至回到地面需要时间为t2-t1=2(s)取h=3.75,得一元二次方程10t-5t2=3.75解方程得t1=0.5;t2=1.5答:球从弹起至回到地面需要时间为2(s);
经过圆心的0.5s或1.5s球的高度达到3.75m.1.不与x轴相交的抛物线是( ).
A. y=2x2-3 B. y=-2x2+3
C. y=-x2-3x D. y=-2(x+1)2-32.若抛物线 y=ax2+bx+c=0,当 a>0,c<0时,图象与x轴交点情况是( ) .
A.无交点 B.只有一个交点
C.有两个交点 D.不能确定DC3.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=___,此时抛物线 y=x2-2x+m与x轴有__个交点.4.已知抛物线 y=x2-8x+c的顶点在 x轴上,则c =__.1116 下列二次函数的图象与x轴有交点吗? 若有,求出交点坐标.
(1)y=2x2+x-3
(2)y=4x2-4x+1
(3)y=x2-x+1令y=0,解一元二次方程的根(1)y=2x2+x-3解:当 y=0 时,2x2+x-3=0,(2x+3)(x-1)=0x1=-1.5 ,x2=1 所以与 x 轴有交点,有两个交点.y=a(x-x1)(x-x1)二次函数的两点式 (2)y=4x2-4x+1解:当y=0时,4x2-4x+1=0,(2x-1)2 =0x1=x2=0.5 所以与 x 轴有一个交点.(3)y=x2-x+1解:当 y=0时,x2-x+1=0, 所以与 x 轴没有交点.因为(-1)2-4×1×1=-3<0,用图像法求一元二次方程 x2+2x-1=0的一个近似解.(精确到0.1) 解:画出函数y=x2+2x-1的图像,如图.
由图像可知,方程两个根,一个在0
和1之间.xO-2-1y12y=x2+2x-1-3●●●求位于0和1之间的根.可由图像可估计这个根是0.4或0.5,见下表. 观察上表,可以发现x取0.4或0.5时,对应的y值由负变正,可见在0.4与0.5之间肯定有一个x的值使y=0.即有方程的一个根. 题目只要求精确到0.1,这时取x=0.4或
x=0.5作为根都符合要求,但当x=0.4时,
y=-0.04比y=0.25(x=0.5)更接近0,故
选x=0.4.
因而,方程x2+2x-1=0在0和1之间精
确到0.1的根为x=0.4.
二次函数的图象与x轴有没有交点,由什么决定?由b2-4ac的符号决定b2-4ac﹥0,有两个交点b2-4ac=0,只有一个交点b2-4ac﹤0,没有交点 求出二次函数y=10x-5x2图象的顶点坐标,与x轴的交点坐标,并画出函数的大致图象.二次函数y=ax2+bx+c 归纳:一元二次方程ax2+bx+c=0两根为x1=m;x2=n则函数与x轴交点坐标为:
(m,0);(n,0) 你能否画出适当的函数图象,求方程的解?他的做法对吗?初三某班的学生在问题中出现争论:
求方程 的解时,几乎所有学生都将方程化为 ,画出函数图象,观察它与x轴的交点,得出方程的解,唯独小刘没有将方程移项,而是分别画出函数y=x2和 的图象,他认为它们的交点A,B的模坐标 和2就是原方程的解.求抛物线 与直线
的交点坐标. (1)当x 取何值时,
当x取何值时,
(2)能否用含有x的不等式来描述(2)中的问题?
在同一坐标系中画出抛物线
与直线 的图象,并回答下列问题
根据图象可求出不等式ax2+bx+c>mx+n或 ax2+bx+c规律:交点的坐标巩固利用函数图象求方程组的解
①在正常水位基础上水位上升 h 米时,桥下水面宽为d 米,求d与h 函数关系式.
②正常水位时,桥下水深2米,为了保证游船顺利通过,桥下水面宽不得小于18 .求水深超过多少会影响过往游船在桥下顺利航行?如图所示,公园要建造圆形喷水池,在水池中央垂直
于水面处安装一个柱子OA,O恰在水面中心,OA=1.25
米,由柱子顶端A处的喷头向外喷水,水流在各个方向沿
形状相同的抛物线落下,
为使水流形状较为美观,
要求设计成水流在离OA
距离为1米处达到距水面
最大高度为2.25米, 如果
不计其他因素, 那么水池
的半径至少要多少米,
才能使喷出的水流不致
落到池外?
解:以水面OC所的直线为 x 轴,柱子OA所在的直线为y轴,O为原点建立直角坐标系,则A、B两点的坐标分别为A(0, 1.25),B(1, 2.25), 设抛物线的解析式为:y = a(x – h) 2 + k, 则有1.25 = a(0 – 1) 2 + 2.25 解得:a = - 1
所以,y = - (x – 1)2 + 2.25令 y = 0, 则
- (x – 1) 2 + 2.25 = 0解得:x = 2.5
或 x = - 0.5 (舍去)
所以,水池半径至少需要2.5米. 练习1:
一男生推铅球,铅球行进高度y(m)与水平距离x(m)之间的函数关系式是: y = - ―x2 + ―x + ―.
(1)画出函数图象;
(2)观察图象,说出铅球推出的距离; 铅球出手时的高度; 铅球行进过程中的最高高度.YX练习2:
如图,在ΔABC中,∠B=90°,点P
从点A开始沿AB边向点B以1厘米/秒的速
度移动,点Q从点B开始沿BC边向点C以
2厘米/秒的速度移动,如果P,Q分别
从A,B同时出发,几秒后ΔABC的面
积最大?最大面积是多少?PQ强化训练你知道吗,平时我们在跳大绳时,绳甩到最高处的形状可以看为抛物线.如图所示,正在甩绳的甲乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙丁分别站在距甲拿绳的手水平距离1米2.5米处,绳子到最高处时刚好通过他们的头顶.已知学生丙的身高是1.5米,求学生丁的身高?归纳:运用二次函数的性质求实际问题的最大值和最小值的一般步骤 :求出函数解析式和自变量的取值范围配方变形,或利用公式求它的最大值或最小值.检查求得的最大值或最小值对应的字变量的值必须在自变量的取值范围内 . 一个球从地面上竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m).已知物体竖直上抛运动中,h=v0t- gt2(v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s2).问球从弹起至回到地面需要多少时间?经多少时间球的高度达到3.75m?地面解:由题意,得h关于t的二次函数
解析式为h=10t-5t2取h=0,得一元二次方程
10t-5t2=0解方程得t1=0;t2=2球从弹起至回到地面需要时间为t2-t1=2(s)取h=3.75,得一元二次方程10t-5t2=3.75解方程得t1=0.5;t2=1.5答:球从弹起至回到地面需要时间为2(s);
经过圆心的0.5s或1.5s球的高度达到3.75m.1.不与x轴相交的抛物线是( ).
A. y=2x2-3 B. y=-2x2+3
C. y=-x2-3x D. y=-2(x+1)2-32.若抛物线 y=ax2+bx+c=0,当 a>0,c<0时,图象与x轴交点情况是( ) .
A.无交点 B.只有一个交点
C.有两个交点 D.不能确定DC3.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=___,此时抛物线 y=x2-2x+m与x轴有__个交点.4.已知抛物线 y=x2-8x+c的顶点在 x轴上,则c =__.1116 下列二次函数的图象与x轴有交点吗? 若有,求出交点坐标.
(1)y=2x2+x-3
(2)y=4x2-4x+1
(3)y=x2-x+1令y=0,解一元二次方程的根(1)y=2x2+x-3解:当 y=0 时,2x2+x-3=0,(2x+3)(x-1)=0x1=-1.5 ,x2=1 所以与 x 轴有交点,有两个交点.y=a(x-x1)(x-x1)二次函数的两点式 (2)y=4x2-4x+1解:当y=0时,4x2-4x+1=0,(2x-1)2 =0x1=x2=0.5 所以与 x 轴有一个交点.(3)y=x2-x+1解:当 y=0时,x2-x+1=0, 所以与 x 轴没有交点.因为(-1)2-4×1×1=-3<0,用图像法求一元二次方程 x2+2x-1=0的一个近似解.(精确到0.1) 解:画出函数y=x2+2x-1的图像,如图.
由图像可知,方程两个根,一个在0
和1之间.xO-2-1y12y=x2+2x-1-3●●●求位于0和1之间的根.可由图像可估计这个根是0.4或0.5,见下表. 观察上表,可以发现x取0.4或0.5时,对应的y值由负变正,可见在0.4与0.5之间肯定有一个x的值使y=0.即有方程的一个根. 题目只要求精确到0.1,这时取x=0.4或
x=0.5作为根都符合要求,但当x=0.4时,
y=-0.04比y=0.25(x=0.5)更接近0,故
选x=0.4.
因而,方程x2+2x-1=0在0和1之间精
确到0.1的根为x=0.4.
二次函数的图象与x轴有没有交点,由什么决定?由b2-4ac的符号决定b2-4ac﹥0,有两个交点b2-4ac=0,只有一个交点b2-4ac﹤0,没有交点 求出二次函数y=10x-5x2图象的顶点坐标,与x轴的交点坐标,并画出函数的大致图象.二次函数y=ax2+bx+c 归纳:一元二次方程ax2+bx+c=0两根为x1=m;x2=n则函数与x轴交点坐标为:
(m,0);(n,0) 你能否画出适当的函数图象,求方程的解?他的做法对吗?初三某班的学生在问题中出现争论:
求方程 的解时,几乎所有学生都将方程化为 ,画出函数图象,观察它与x轴的交点,得出方程的解,唯独小刘没有将方程移项,而是分别画出函数y=x2和 的图象,他认为它们的交点A,B的模坐标 和2就是原方程的解.求抛物线 与直线
的交点坐标. (1)当x 取何值时,
当x取何值时,
(2)能否用含有x的不等式来描述(2)中的问题?
在同一坐标系中画出抛物线
与直线 的图象,并回答下列问题
根据图象可求出不等式ax2+bx+c>mx+n或 ax2+bx+c
