19.2.1 菱形的性质同步练习
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
19.2.1 菱形的性质同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.有一组邻边相等的平行四边形是菱形,菱形既是轴对称图形,也是中心对称图形.
2.菱形的性质定理1:菱形的四条边都相等.
3.菱形的性质定理2:菱形的对角线互相垂直平分.
4.菱形的面积与两条对角线的关系是 菱形的面积等于两条对角线乘积的一 半.
基础知识和能力拓展精练
一.选择题
1.边长为5cm的菱形的周长是( )
A.10cm B.15cm C.20cm D.25cm
2.菱形具有而一般平行四边形不具有的性质是( )
A.对边相等 B.对角相等
C.对角线互相垂直 D.对角线互相平分
3.如图,在菱形ABCD中,对角线AC=4,BD=9,则菱形ABCD的面积为( )
A.12 B.18 C.20 D.36
4.如图,已知菱形ABCD的边长为4,∠ABC=120°,过B作BE⊥AD,则BE的长为( )
A. B. C.2 D.1
5.如图,在菱形ABCD中,P、Q分别是AD、AC的中点,如果PQ=3,那么菱形ABCD的周长是( )
A.30 B.24 C.18 D.6
6.已知:在平面直角坐标系中,菱形ABCD三个顶点的坐标分别是A(﹣2,0)、B(0,1)、C(2,0),则点D的坐标是( )
A.(﹣4,﹣1) B.(4,﹣1) C.(0,﹣1) D.(0,﹣2)
7.在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点,则∠EAF等于( )
A.60° B.55° C.45° D.30°
8.在菱形ABCD中,下列结论错误的是( )
A.BO=DO B.∠DAC=∠BAC C.AC⊥BD D.AO=DO
二.填空题
9.已知菱形ABCD的面积是12cm2,一条对角线长为4cm,则菱形的边长是 cm.
10.如图,在菱形ABCD中,∠ABC=120°,E、F分别是AB、AD的中点,若EF=3,则菱形ABCD的边长是 .
11.菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2014秒时,点P的坐标为 .
12.如图,在菱形ABCD中,AB=6,∠B=60°,点G是边CD边的中点,点E、F分别是AG、AD上的两个动点,则EF+ED的最小值是 .
三.解答题
13.已知菱形ABCD的周长为48cm,两个邻角∠A与∠B的比是1:2,求这个菱形的面积.
14.如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.求:
(1)两条小路的长度;
(2)菱形花坛的面积.(结果保留根号)
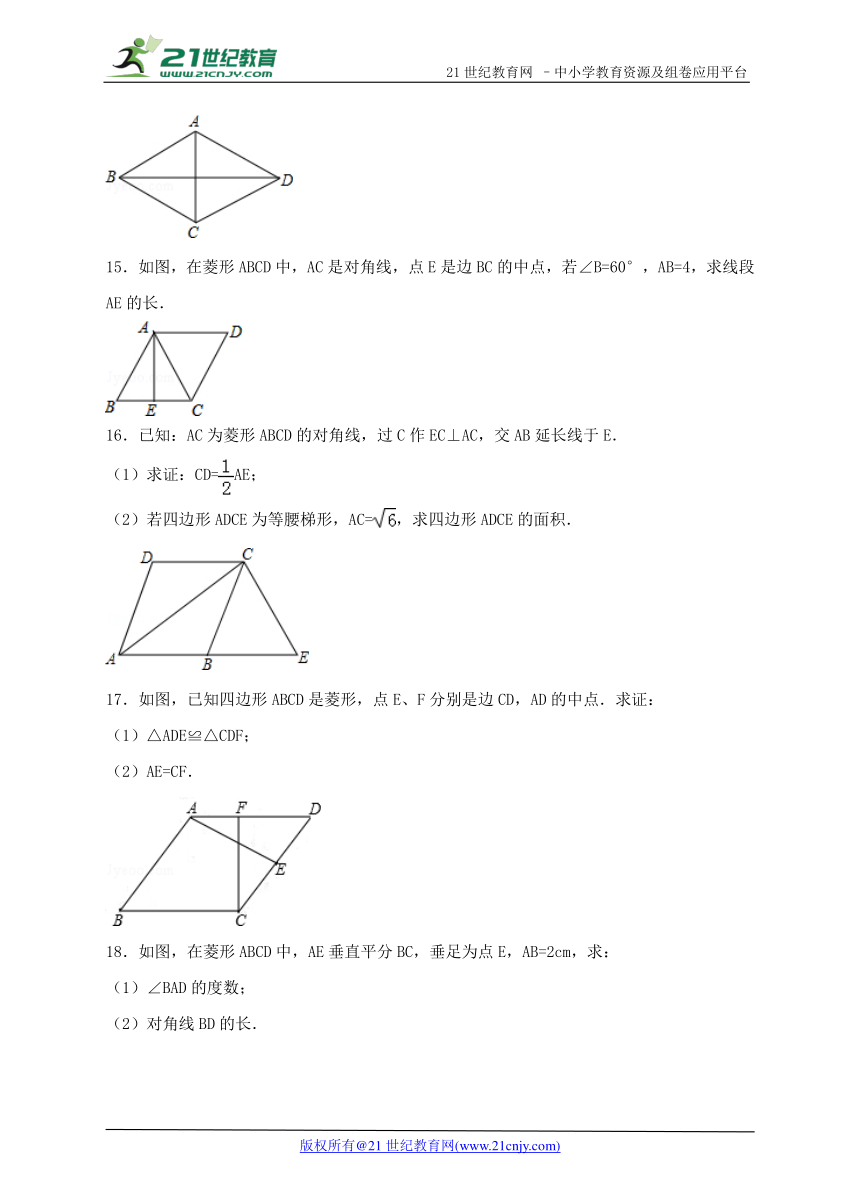
15.如图,在菱形ABCD中,AC是对角线,点E是边BC的中点,若∠B=60°,AB=4,求线段AE的长.
16.已知:AC为菱形ABCD的对角线,过C作EC⊥AC,交AB延长线于E.
(1)求证:CD=AE;
(2)若四边形ADCE为等腰梯形,AC=,求四边形ADCE的面积.
17.如图,已知四边形ABCD是菱形,点E、F分别是边CD,AD的中点.求证:
(1)△ADE≌△CDF;
(2)AE=CF.
18.如图,在菱形ABCD中,AE垂直平分BC,垂足为点E,AB=2cm,求:
(1)∠BAD的度数;
(2)对角线BD的长.
19.已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点.
(1)求菱形ABCD的面积.
(2)求PM+PN的最小值.
20.感知:如图①,在菱形ABCD中,AB=BD,点E、F分别在边AB、AD上.若AE=DF,易知△ADE≌△DBF.
探究:如图②,在菱形ABCD中,AB=BD,点E、F分别在BA、AD的延长线上.若AE=DF,△ADE与△DBF是否全等?如果全等,请证明;如果不全等,请说明理由.
拓展:如图③,在 ABCD中,AD=BD,点O是AD边的垂直平分线与BD的交点,点E、F分别在OA、AD的延长线上.若AE=DF,∠ADB=50°,∠AFB=32°,求∠ADE的度数.
参考答案与试题解析
一.选择题
1.
【分析】利用菱形的各边长相等,进而求出周长即可.
解:∵菱形的各边长相等,
∴边长为5cm的菱形的周长是:5×4=20(cm).
故选:C.
2.
【分析】由菱形具有的性质是:对边相等,对角相等,对角线互相垂直且平分;平行四边形具有的性质是:对边相等,对角相等,对角线互相平分;即可求得答案.
解:∵菱形具有的性质是:对边相等,对角相等,对角线互相垂直且平分;平行四边形具有的性质是:对边相等,对角相等,对角线互相平分;
∴菱形具有而一般平行四边形不具有的性质是:对角线互相垂直.
故选:C.
3.
【分析】由菱形ABCD的对角线AC=4,BD=9,根据菱形的面积等于其对角线积的一半,即可求得菱形ABCD的面积.
解:∵菱形ABCD的对角线AC=4,BD=9,
∴菱形ABCD的面积为:AC BD=×4×9=18.
故选:B.
4.
【分析】根据菱形的性质可求得∠A=60°,在Rt△ABE中由三角函数的定义可求得BE.
解:∵四边形ABCD为菱形,
∴AD∥BC,
∴∠A+∠ABC=180°,
∴∠A=180°﹣120°=60°,
∵BE⊥AD,
∴sinA=,
∴BE=AB sin60°=4×=2,
故选:A.
5.
【分析】根据题意得PQ是△ADC的中位线,从而可求得菱形的边长,则菱形的周长就不难求得了.
解:由题意可知,PQ是△ADC的中位线,则DC=2PQ=2×3=6,那么菱形ABCD的周长=6×4=24,
故选:B.
6.
【分析】根据题意画出坐标系,在坐标系内描出各点,根据菱形的性质即可得出结论.
解:如图所示,
∵菱形的对角线互相垂直平分,
∴D(0,﹣1).
故选:C.
7.
【分析】连接AC,根据线段垂直平分线上的点到线段两端段的可得AB=AC,然后求出△ABC是等边三角形,再根据等边三角形的性质求出∠CAE=30°,同理可得∠CAF=30°,然后根据∠EAF=∠CAE+∠CAF计算即可得解.
解:如图,连接AC,
∵AE⊥BC,点E是BC的中点,
∴AB=AC,
∵四边形ABCD是菱形,
∴AB=BC,
∴△ABC是等边三角形,
∴∠CAE=30°,
同理可得∠CAF=30°,
∴∠EAF=∠CAE+∠CAF=30°+30°=60°.
故选:A.
8.
【分析】根据菱形的两条对角线互相垂直且平分,并且每一条对角线平分一组对角;即可求得答案.
解:∵四边形ABCD是菱形,
∴AC⊥BD,∠DAC=∠BAC,BO=DO,
故A,B,C正确,D错误.
故选:D.
二.填空题(共5小题)
9.
【分析】根据菱形的面积公式求出另一对角线的长.然后因为菱形的对角线互相垂直平分,利用勾股定理求出菱形的边长.
解:由菱形的面积公式,可得另一对角线长12×2÷4=6,
∵菱形的对角线互相垂直平分,
根据勾股定理可得菱形的边长==cm.
故答案为.
10.
【分析】易证△ABD是等边三角形,再根据中位线定理易求BD.
解:∵四边形ABCD是菱形,∠ABC=120°,
∴AB=AD,∠A=60°,
∴△ABD是等边三角形,
∴AB=AD=BD,
∵E、F分别是AB、AD的中点,
∴AB=BD=2EF=2×3=6.
故答案为:6.
11.
【分析】先根据勾股定理求出菱形的边长,再根据点P的运动速度求出沿A→B→C→D→A所需的时间,进而可得出结论.
解:∵A(1,0),B(0,),
∴AB==2.
∵点P的运动速度为0.5米/秒,
∴从点A到点B所需时间==4秒,
∴沿A→B→C→D→A所需的时间=4×4=16秒,
∵=125…14,
∴移动到第2014秒和第14秒的位置相同,当P运动到第14秒时,如图所示,作PE⊥AC于E,PF⊥OD于F.
可得 =,
∴PA=PD,
∴P(,﹣)
故答案为:( ,﹣).
12.
【分析】作DH⊥AC垂足为H与AG交于点E,点H关于AG的对称点为F,此时EF+ED最小=DH,先证明△ADC是等边三角形,在RT△DCH中利用勾股定理即可解决问题.
解:如图作DH⊥AC垂足为H与AG交于点E,
∵四边形ABCD是菱形,
∵AB=AD=CD=BC=6,
∵∠B=60°,
∴∠ADC=∠B=60°,
∴△ADC是等边三角形,
∵AG是中线,
∴∠GAD=∠GAC
∴点H关于AG的对称点F在AD上,此时EF+ED最小=DH.
在RT△DHC中,∵∠DHC=90°,DC=6,∠CDH=∠ADC=30°,
∴CH=DC=3,DH===3,
∴EF+DE的最小值=DH=3
故答案为3.
三.解答题(共8小题)
13.
【分析】首先过点D作DE⊥AB于点E,由菱形ABCD的周长为48cm,可求得其边长,由两个邻角∠A与∠B的比是1:2,可求得∠A=60°,然后由三角函数,求得DE的长,继而求得这个菱形的面积.
解:过点D作DE⊥AB于点E,
∵菱形ABCD的两个邻角∠A与∠B的比是1:2,
∴∠A=60°,
∵菱形ABCD的周长为48cm,
∴AB=AD=12cm,
∴DE=AD sin60°=6(cm),
∴这个菱形的面积为:AB DE=12×6=72(cm2).
14.
【分析】(1)根据菱形的对角线互相垂直平分可得AC⊥BD,AC=2AO,BD=2BO,菱形的对角线平分一组对角线可得∠ABO=∠ABC=30°,根据直角三角形30°角所对的直角边等于斜边的一半可得AO=AB,再利用勾股定理列式求出BO,然后求出AC、BD即可;
(2)根据菱形的面积等于对角线乘积的一半列式计算即可得解.
解:(1)∵花坛ABCD是菱形,
∴AC⊥BD,AC=2AO,BD=2BO,∠ABO=∠ABC=×60°=30°,
∴Rt△ABO中,AO=AB=×20=10m,
∴BO===10cm,
∴AC=2AO=20m,BD=2BO=20m;
(2)S菱形ABCD=AC BD=×20×20=200m2.
答:菱形花坛的面积是200m2.
15.
【分析】根据菱形的性质得出AB=BC,进而得出△ABC是等边三角形,再利用等边三角形的性质得出BE=2,再利用勾股定理求出AB的长.
解:∵四边形ABCD是菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC是等边三角形,
∵E是BC的中点,
∴AE⊥BC,∠BAE=∠B=30°,
∵AB=4,
∴BE=2,
在Rt△ABE中,
AE===2.
16.
【分析】(1)利用菱形的性质得出EC∥BF,再利用平行线分线段成比例定理得出AB=BE,则AB=BE=CD进而得出答案;
(2)利用等腰梯形以及菱形的性质得出CE=AE,进而利用勾股定理得出CM的长,再利用梯形面积求法得出即可.
(1)证明:连接BD,
∵AC、BD为菱形ABCD的对角线,
∴AC⊥BD,AF=CF,AB=BC,
∵EC⊥AC,
∴EC∥BF,
∴AB=BE,
∴AB=BE=CD,
∴CD=AE;
(2)解:过点C作CM⊥AE于点M,
∵四边形ADCE为等腰梯形,
∴AD=EC,
∵CD=AE,CE=AD=CD,
∴CE=AE,
设CE=x,则AE=2x,
∵AC=,
∴x2+()2=(2x)2,
解得:x=±(负数舍去),
∴CM×AE=AC×EC,
∴2CM=×,
解得:CM=,
∴四边形ADCE的面积为:(CD+AE)×CM=(+2)×=.
17.
【分析】(1)根据菱形的性质得出对应边相等,进而利用SAS得出即可;
(2)利用(1)中所求,得出答案.
证明:(1)∵四边形ABCD是菱形,点E、F分别是边CD,AD的中点,
∴DF=DE,AD=CD,
在△ADE和△CDF中
,
∴△ADE≌△CDF(SAS);
(2)∵△ADE≌△CDF,
∴AE=CF.
18.
【分析】(1)根据菱形性质得出AD∥BC,AB=BC=2cm,求出AB=2BE,推出∠BAE=30°,求出∠ABE=60°,根据平行线性质推出即可.
(2)根据菱形性质得出BD=2BO,∠ABD=∠CBD=∠ABC=30°,AC⊥BD,求出OC,根据勾股定理求出BO=cm,即可求出答案.
解:(1)∵四边形ABCD是菱形,
∴AD∥BC,AB=BC=2cm,
∵AE垂直平分BC,
∴∠AEB=90°,BE=BC=1cm,
即AB=2BE,
∴∠BAE=30°,
∴∠ABE=180°﹣90°﹣30°=60°,
∵AD∥BC,
∴∠BAD=180°﹣∠ABC=120°.
(2)∵四边形ABCD是菱形,
∴BD=2BO,∠ABD=∠CBD=∠ABC=30°,AC⊥BD,
∴∠BOC=90°,
∵∠CBO=30°,
∴OC=BC=1cm,
由勾股定理得:BO===(cm),
∴BD=2BO=2cm.
19.
【分析】(1)利用菱形ABCD的两条对角线乘积的一半等于菱形面积求出即可;
(2)利用已知得出四边形BQNC是平行四边形,则NQ=BC,再利用菱形的性质以及勾股定理得出MP+NP=QP+NP=QN的值.
解:(1)∵菱形ABCD的两条对角线分别为6和8,
∴菱形ABCD的面积为:×6×8=24;
(2)作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,
连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,
即Q在AB上,
∵MQ⊥BD,
∴AC∥MQ,
∵M为BC中点,
∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN,
∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,
∴CP=AC=3,BP=BD=4,
在Rt△BPC中,由勾股定理得:BC=5,
即NQ=5,
∴MP+NP=QP+NP=QN=5,
∴PM+PN的最小值为:5.
20.
【分析】探究:△ADE和△DBF全等,利用菱形的性质首先证明三角形ABD为等边三角形,再利用全等三角形的判定方法即可证明△ADE≌△DBF;
拓展:因为点O在AD的垂直平分线上,所以OA=OD,再通过证明△ADE≌△DBF,利用全等三角形的性质即可求出∠ADE的度数.
解:
探究:△ADE和△DBF全等.
∵四边形ABCD是菱形,
∴AB=AD.
∵AB=BD,
∴AB=AD=BD.
∴△ABD为等边三角形.
∴∠DAB=∠ADB=60°.
∴∠EAD=∠FDB=120°.
∵AE=DF,
∴△ADE≌△DBF;
拓展:
∵点O在AD的垂直平分线上,
∴OA=OD.
∴∠DAO=∠ADB=50°.
∴∠EAD=∠FDB.
∵AE=DF,AD=DB,
∴△ADE≌△DBF.
∴∠DEA=∠AFB=32°.
∴∠EDA=18°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
19.2.1 菱形的性质同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.有一组邻边相等的平行四边形是菱形,菱形既是轴对称图形,也是中心对称图形.
2.菱形的性质定理1:菱形的四条边都相等.
3.菱形的性质定理2:菱形的对角线互相垂直平分.
4.菱形的面积与两条对角线的关系是 菱形的面积等于两条对角线乘积的一 半.
基础知识和能力拓展精练
一.选择题
1.边长为5cm的菱形的周长是( )
A.10cm B.15cm C.20cm D.25cm
2.菱形具有而一般平行四边形不具有的性质是( )
A.对边相等 B.对角相等
C.对角线互相垂直 D.对角线互相平分
3.如图,在菱形ABCD中,对角线AC=4,BD=9,则菱形ABCD的面积为( )
A.12 B.18 C.20 D.36
4.如图,已知菱形ABCD的边长为4,∠ABC=120°,过B作BE⊥AD,则BE的长为( )
A. B. C.2 D.1
5.如图,在菱形ABCD中,P、Q分别是AD、AC的中点,如果PQ=3,那么菱形ABCD的周长是( )
A.30 B.24 C.18 D.6
6.已知:在平面直角坐标系中,菱形ABCD三个顶点的坐标分别是A(﹣2,0)、B(0,1)、C(2,0),则点D的坐标是( )
A.(﹣4,﹣1) B.(4,﹣1) C.(0,﹣1) D.(0,﹣2)
7.在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点,则∠EAF等于( )
A.60° B.55° C.45° D.30°
8.在菱形ABCD中,下列结论错误的是( )
A.BO=DO B.∠DAC=∠BAC C.AC⊥BD D.AO=DO
二.填空题
9.已知菱形ABCD的面积是12cm2,一条对角线长为4cm,则菱形的边长是 cm.
10.如图,在菱形ABCD中,∠ABC=120°,E、F分别是AB、AD的中点,若EF=3,则菱形ABCD的边长是 .
11.菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2014秒时,点P的坐标为 .
12.如图,在菱形ABCD中,AB=6,∠B=60°,点G是边CD边的中点,点E、F分别是AG、AD上的两个动点,则EF+ED的最小值是 .
三.解答题
13.已知菱形ABCD的周长为48cm,两个邻角∠A与∠B的比是1:2,求这个菱形的面积.
14.如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.求:
(1)两条小路的长度;
(2)菱形花坛的面积.(结果保留根号)
15.如图,在菱形ABCD中,AC是对角线,点E是边BC的中点,若∠B=60°,AB=4,求线段AE的长.
16.已知:AC为菱形ABCD的对角线,过C作EC⊥AC,交AB延长线于E.
(1)求证:CD=AE;
(2)若四边形ADCE为等腰梯形,AC=,求四边形ADCE的面积.
17.如图,已知四边形ABCD是菱形,点E、F分别是边CD,AD的中点.求证:
(1)△ADE≌△CDF;
(2)AE=CF.
18.如图,在菱形ABCD中,AE垂直平分BC,垂足为点E,AB=2cm,求:
(1)∠BAD的度数;
(2)对角线BD的长.
19.已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点.
(1)求菱形ABCD的面积.
(2)求PM+PN的最小值.
20.感知:如图①,在菱形ABCD中,AB=BD,点E、F分别在边AB、AD上.若AE=DF,易知△ADE≌△DBF.
探究:如图②,在菱形ABCD中,AB=BD,点E、F分别在BA、AD的延长线上.若AE=DF,△ADE与△DBF是否全等?如果全等,请证明;如果不全等,请说明理由.
拓展:如图③,在 ABCD中,AD=BD,点O是AD边的垂直平分线与BD的交点,点E、F分别在OA、AD的延长线上.若AE=DF,∠ADB=50°,∠AFB=32°,求∠ADE的度数.
参考答案与试题解析
一.选择题
1.
【分析】利用菱形的各边长相等,进而求出周长即可.
解:∵菱形的各边长相等,
∴边长为5cm的菱形的周长是:5×4=20(cm).
故选:C.
2.
【分析】由菱形具有的性质是:对边相等,对角相等,对角线互相垂直且平分;平行四边形具有的性质是:对边相等,对角相等,对角线互相平分;即可求得答案.
解:∵菱形具有的性质是:对边相等,对角相等,对角线互相垂直且平分;平行四边形具有的性质是:对边相等,对角相等,对角线互相平分;
∴菱形具有而一般平行四边形不具有的性质是:对角线互相垂直.
故选:C.
3.
【分析】由菱形ABCD的对角线AC=4,BD=9,根据菱形的面积等于其对角线积的一半,即可求得菱形ABCD的面积.
解:∵菱形ABCD的对角线AC=4,BD=9,
∴菱形ABCD的面积为:AC BD=×4×9=18.
故选:B.
4.
【分析】根据菱形的性质可求得∠A=60°,在Rt△ABE中由三角函数的定义可求得BE.
解:∵四边形ABCD为菱形,
∴AD∥BC,
∴∠A+∠ABC=180°,
∴∠A=180°﹣120°=60°,
∵BE⊥AD,
∴sinA=,
∴BE=AB sin60°=4×=2,
故选:A.
5.
【分析】根据题意得PQ是△ADC的中位线,从而可求得菱形的边长,则菱形的周长就不难求得了.
解:由题意可知,PQ是△ADC的中位线,则DC=2PQ=2×3=6,那么菱形ABCD的周长=6×4=24,
故选:B.
6.
【分析】根据题意画出坐标系,在坐标系内描出各点,根据菱形的性质即可得出结论.
解:如图所示,
∵菱形的对角线互相垂直平分,
∴D(0,﹣1).
故选:C.
7.
【分析】连接AC,根据线段垂直平分线上的点到线段两端段的可得AB=AC,然后求出△ABC是等边三角形,再根据等边三角形的性质求出∠CAE=30°,同理可得∠CAF=30°,然后根据∠EAF=∠CAE+∠CAF计算即可得解.
解:如图,连接AC,
∵AE⊥BC,点E是BC的中点,
∴AB=AC,
∵四边形ABCD是菱形,
∴AB=BC,
∴△ABC是等边三角形,
∴∠CAE=30°,
同理可得∠CAF=30°,
∴∠EAF=∠CAE+∠CAF=30°+30°=60°.
故选:A.
8.
【分析】根据菱形的两条对角线互相垂直且平分,并且每一条对角线平分一组对角;即可求得答案.
解:∵四边形ABCD是菱形,
∴AC⊥BD,∠DAC=∠BAC,BO=DO,
故A,B,C正确,D错误.
故选:D.
二.填空题(共5小题)
9.
【分析】根据菱形的面积公式求出另一对角线的长.然后因为菱形的对角线互相垂直平分,利用勾股定理求出菱形的边长.
解:由菱形的面积公式,可得另一对角线长12×2÷4=6,
∵菱形的对角线互相垂直平分,
根据勾股定理可得菱形的边长==cm.
故答案为.
10.
【分析】易证△ABD是等边三角形,再根据中位线定理易求BD.
解:∵四边形ABCD是菱形,∠ABC=120°,
∴AB=AD,∠A=60°,
∴△ABD是等边三角形,
∴AB=AD=BD,
∵E、F分别是AB、AD的中点,
∴AB=BD=2EF=2×3=6.
故答案为:6.
11.
【分析】先根据勾股定理求出菱形的边长,再根据点P的运动速度求出沿A→B→C→D→A所需的时间,进而可得出结论.
解:∵A(1,0),B(0,),
∴AB==2.
∵点P的运动速度为0.5米/秒,
∴从点A到点B所需时间==4秒,
∴沿A→B→C→D→A所需的时间=4×4=16秒,
∵=125…14,
∴移动到第2014秒和第14秒的位置相同,当P运动到第14秒时,如图所示,作PE⊥AC于E,PF⊥OD于F.
可得 =,
∴PA=PD,
∴P(,﹣)
故答案为:( ,﹣).
12.
【分析】作DH⊥AC垂足为H与AG交于点E,点H关于AG的对称点为F,此时EF+ED最小=DH,先证明△ADC是等边三角形,在RT△DCH中利用勾股定理即可解决问题.
解:如图作DH⊥AC垂足为H与AG交于点E,
∵四边形ABCD是菱形,
∵AB=AD=CD=BC=6,
∵∠B=60°,
∴∠ADC=∠B=60°,
∴△ADC是等边三角形,
∵AG是中线,
∴∠GAD=∠GAC
∴点H关于AG的对称点F在AD上,此时EF+ED最小=DH.
在RT△DHC中,∵∠DHC=90°,DC=6,∠CDH=∠ADC=30°,
∴CH=DC=3,DH===3,
∴EF+DE的最小值=DH=3
故答案为3.
三.解答题(共8小题)
13.
【分析】首先过点D作DE⊥AB于点E,由菱形ABCD的周长为48cm,可求得其边长,由两个邻角∠A与∠B的比是1:2,可求得∠A=60°,然后由三角函数,求得DE的长,继而求得这个菱形的面积.
解:过点D作DE⊥AB于点E,
∵菱形ABCD的两个邻角∠A与∠B的比是1:2,
∴∠A=60°,
∵菱形ABCD的周长为48cm,
∴AB=AD=12cm,
∴DE=AD sin60°=6(cm),
∴这个菱形的面积为:AB DE=12×6=72(cm2).
14.
【分析】(1)根据菱形的对角线互相垂直平分可得AC⊥BD,AC=2AO,BD=2BO,菱形的对角线平分一组对角线可得∠ABO=∠ABC=30°,根据直角三角形30°角所对的直角边等于斜边的一半可得AO=AB,再利用勾股定理列式求出BO,然后求出AC、BD即可;
(2)根据菱形的面积等于对角线乘积的一半列式计算即可得解.
解:(1)∵花坛ABCD是菱形,
∴AC⊥BD,AC=2AO,BD=2BO,∠ABO=∠ABC=×60°=30°,
∴Rt△ABO中,AO=AB=×20=10m,
∴BO===10cm,
∴AC=2AO=20m,BD=2BO=20m;
(2)S菱形ABCD=AC BD=×20×20=200m2.
答:菱形花坛的面积是200m2.
15.
【分析】根据菱形的性质得出AB=BC,进而得出△ABC是等边三角形,再利用等边三角形的性质得出BE=2,再利用勾股定理求出AB的长.
解:∵四边形ABCD是菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC是等边三角形,
∵E是BC的中点,
∴AE⊥BC,∠BAE=∠B=30°,
∵AB=4,
∴BE=2,
在Rt△ABE中,
AE===2.
16.
【分析】(1)利用菱形的性质得出EC∥BF,再利用平行线分线段成比例定理得出AB=BE,则AB=BE=CD进而得出答案;
(2)利用等腰梯形以及菱形的性质得出CE=AE,进而利用勾股定理得出CM的长,再利用梯形面积求法得出即可.
(1)证明:连接BD,
∵AC、BD为菱形ABCD的对角线,
∴AC⊥BD,AF=CF,AB=BC,
∵EC⊥AC,
∴EC∥BF,
∴AB=BE,
∴AB=BE=CD,
∴CD=AE;
(2)解:过点C作CM⊥AE于点M,
∵四边形ADCE为等腰梯形,
∴AD=EC,
∵CD=AE,CE=AD=CD,
∴CE=AE,
设CE=x,则AE=2x,
∵AC=,
∴x2+()2=(2x)2,
解得:x=±(负数舍去),
∴CM×AE=AC×EC,
∴2CM=×,
解得:CM=,
∴四边形ADCE的面积为:(CD+AE)×CM=(+2)×=.
17.
【分析】(1)根据菱形的性质得出对应边相等,进而利用SAS得出即可;
(2)利用(1)中所求,得出答案.
证明:(1)∵四边形ABCD是菱形,点E、F分别是边CD,AD的中点,
∴DF=DE,AD=CD,
在△ADE和△CDF中
,
∴△ADE≌△CDF(SAS);
(2)∵△ADE≌△CDF,
∴AE=CF.
18.
【分析】(1)根据菱形性质得出AD∥BC,AB=BC=2cm,求出AB=2BE,推出∠BAE=30°,求出∠ABE=60°,根据平行线性质推出即可.
(2)根据菱形性质得出BD=2BO,∠ABD=∠CBD=∠ABC=30°,AC⊥BD,求出OC,根据勾股定理求出BO=cm,即可求出答案.
解:(1)∵四边形ABCD是菱形,
∴AD∥BC,AB=BC=2cm,
∵AE垂直平分BC,
∴∠AEB=90°,BE=BC=1cm,
即AB=2BE,
∴∠BAE=30°,
∴∠ABE=180°﹣90°﹣30°=60°,
∵AD∥BC,
∴∠BAD=180°﹣∠ABC=120°.
(2)∵四边形ABCD是菱形,
∴BD=2BO,∠ABD=∠CBD=∠ABC=30°,AC⊥BD,
∴∠BOC=90°,
∵∠CBO=30°,
∴OC=BC=1cm,
由勾股定理得:BO===(cm),
∴BD=2BO=2cm.
19.
【分析】(1)利用菱形ABCD的两条对角线乘积的一半等于菱形面积求出即可;
(2)利用已知得出四边形BQNC是平行四边形,则NQ=BC,再利用菱形的性质以及勾股定理得出MP+NP=QP+NP=QN的值.
解:(1)∵菱形ABCD的两条对角线分别为6和8,
∴菱形ABCD的面积为:×6×8=24;
(2)作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,
连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,
即Q在AB上,
∵MQ⊥BD,
∴AC∥MQ,
∵M为BC中点,
∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN,
∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,
∴CP=AC=3,BP=BD=4,
在Rt△BPC中,由勾股定理得:BC=5,
即NQ=5,
∴MP+NP=QP+NP=QN=5,
∴PM+PN的最小值为:5.
20.
【分析】探究:△ADE和△DBF全等,利用菱形的性质首先证明三角形ABD为等边三角形,再利用全等三角形的判定方法即可证明△ADE≌△DBF;
拓展:因为点O在AD的垂直平分线上,所以OA=OD,再通过证明△ADE≌△DBF,利用全等三角形的性质即可求出∠ADE的度数.
解:
探究:△ADE和△DBF全等.
∵四边形ABCD是菱形,
∴AB=AD.
∵AB=BD,
∴AB=AD=BD.
∴△ABD为等边三角形.
∴∠DAB=∠ADB=60°.
∴∠EAD=∠FDB=120°.
∵AE=DF,
∴△ADE≌△DBF;
拓展:
∵点O在AD的垂直平分线上,
∴OA=OD.
∴∠DAO=∠ADB=50°.
∴∠EAD=∠FDB.
∵AE=DF,AD=DB,
∴△ADE≌△DBF.
∴∠DEA=∠AFB=32°.
∴∠EDA=18°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
