20.3 数据的离散程度同步练习
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
20.3 数据的离散程度同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.(1)方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.
(2)用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况,这个结果叫方差,通常用s2来表示,计算公式是:
s2= [(x1-x )2+(x2-x )2+…+(xn-x )2](可简单记忆为“方差等于差方的平均数”)
(3)方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.21教育名师原创作品
2.求一组数据的平均数、标准差和方差都可以用计算器来计算.
基础知识和能力拓展精练
一、选择题
1.下列说法正确的是( )
A.方差越大,数据的波动越大
B.某种彩票中奖概率为1%,是指买100张彩票一定有1张中奖
C.旅客上飞机前的安检应采用抽样调查
D.掷一枚硬币,正面一定朝上
2.甲、乙、丙、丁四人进行射击测试,每人 ( http: / / www.21cnjy.com )10次射击的平均成绩都为9环,方差分别为S甲2=0.56,S乙2=0.62,S丙2=0.39,S丁2=0.42,则四人中成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
3.2013年安庆市体育考试跳绳项目为学生 ( http: / / www.21cnjy.com )选考项目,下表是某班模拟考试时10名同学的测试成绩(单位:个/分钟),则关于这10名同学每分钟跳绳的测试成绩,下列说法错误的是( )
成绩(个/分钟) 140 160 169 170 177 180
人数 1 1 1 2 3 2
A.众数是177B.平均数是170C.中位数是173.5D.方差是135
4.某数学兴趣小组6名成员通过一次数学竞赛进行组内评比,他们的成绩分别是89,92,91,93,96,91,则关于这组数据说法正确的有( )
A.中位数是92.5 B.平均数是92 C.众数是96 D.方差是5
5.数据1,2,3,4,5的方差为2,则3,5,7,9,11的方差为( )
A.6 B.7 C.8 D.9
6.某校八年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛.各参赛选手成绩的数据分析如下表所示,则以下判断错误的是( )
班级 平均数 中位数 众数 方差
八(1)班 94 93 94 12
八(2)班 95 95.5 93 8.4
A.八(2)班的总分高于八(1)班 B.八(2)班的成绩比八(1)班稳定
C.八(2)班的成绩集中在中上游 D.两个班的最高分在八(2)班
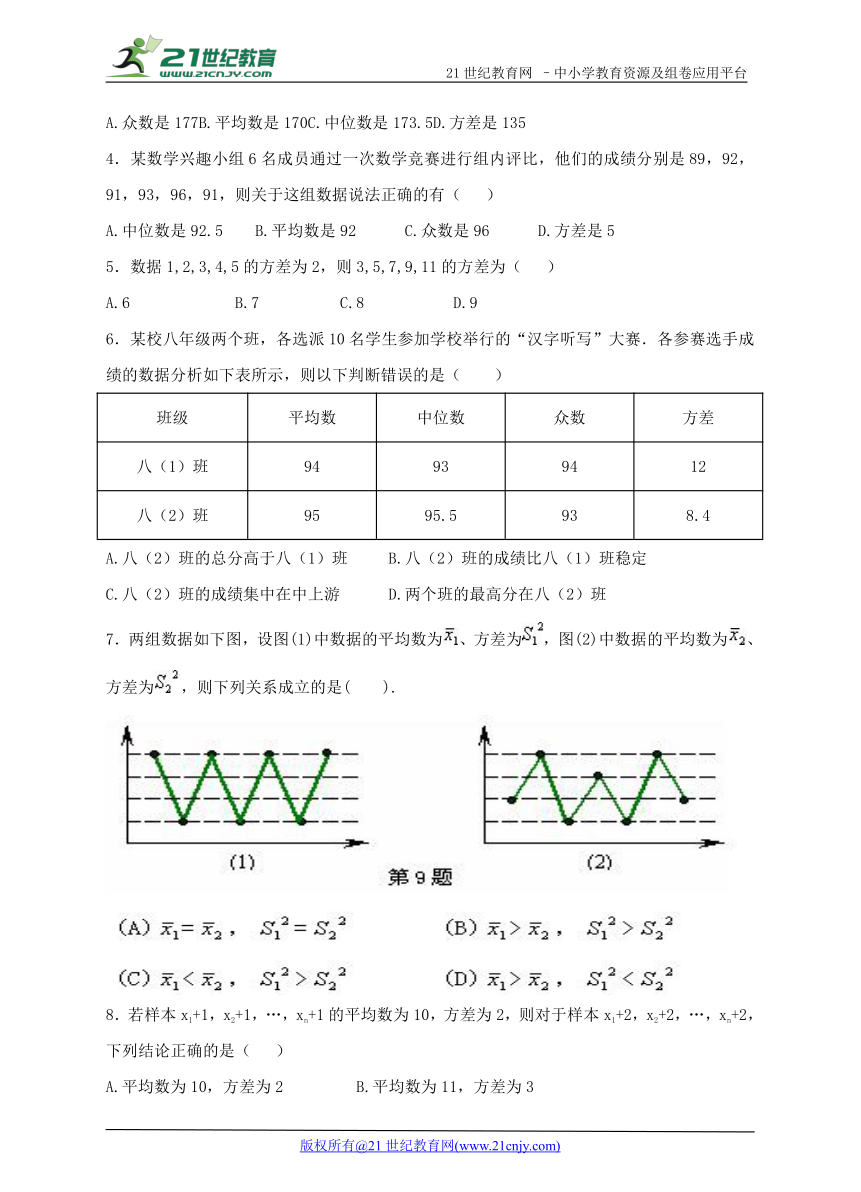
7.两组数据如下图,设图(1)中数据的平均数为 ( http: / / www.21cnjy.com )、方差为 ( http: / / www.21cnjy.com ),图(2)中数据的平均数为 ( http: / / www.21cnjy.com )、方差为 ( http: / / www.21cnjy.com ),则下列关系成立的是( ).21世纪教育网版权所有
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
8.若样本x1+1,x2+1,…,xn+1的平均数为10,方差为2,则对于样本x1+2,x2+2,…,xn+2,下列结论正确的是( )21cnjy.com
A.平均数为10,方差为2 B.平均数为11,方差为3
C.平均数为11,方差为2 D.平均数为12,方差为4
二、填空题
9.数据3,3,6,5,3的方差是_____.
10.下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
方差 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
根据表中数据,要从甲、乙、丙、丁中选择一名成绩好又发挥稳定的运动员参加决赛,应该选择__________.21·世纪*教育网
11.一组数据的方差是,…,则这组数据共有_______个,平均数是________.
12.甲乙两地9月上旬的日平均气温如图所示,则甲乙两地这10天日平均气温方差大小关系为(填>或<).21*cnjy*com
( http: / / www.21cnjy.com )
13.甲、乙、丙三位选手各10次射击成绩的平均数和方差,统计如下表:
选手 甲 乙 丙
平均数 9.3 9.3 9.3
方差 0.026 0.015 0.032
则射击成绩最稳定的选手是________.(填“甲”“乙”“丙”中的一个)
14.已知一组数据x1,x2,x3,平均数和方差分别是2,,那么另一组数据2x1–1,2x2–1,2x3–1的平均数和方差分别是_______,___________.
15.设x1,x2,…,xn平均数为,方差为.若,则x1,x2,…,xn应满足的条件是________________.
三、解答题
16.甲、乙两个电子厂在广告中都声称他们的 ( http: / / www.21cnjy.com )某种电子产品在正常情况下的使用寿命都是5年.质检部门对这两家销售的产品的使用寿命进行了跟踪调查,统计结果如下:(单位:年)
甲厂:3,4,5,6,7 乙厂:4,4,5,6,6
(1)分别求出甲、乙两厂的该种电子产品在正常情况下的使用寿命的平均数和方差;
(2)如果你是顾客,你会选购哪家电子厂的产品?说明理由.
17.某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
(1)请你根据左图填写右表:
销售公司 平均数 方差 中位数 众数
甲 9
乙 9 17.0 8
( http: / / www.21cnjy.com )
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势
看(分析哪个汽车销售公司较有潜力).
18.某射击队为了解运动员的年龄情况,作了一次年龄调查,根据射击运动员的年龄(单位:岁),绘制出如下的统计图.
(1)你能利用该统计图求出平均数、众数和中位数中的哪些统计量?并直接写出结果;
(2)小颖认为,若从该射击队中任意挑选四名队员,则必有一名队员的年龄是15岁.你认为她的判断正确吗?为什么?
(3)小亮认为,可用该统计图求出方差.你认同他的看法吗?若认同,请求出方差;若不认同,请说明理由.
( http: / / www.21cnjy.com )
19.某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图
(1)该商场这段时间内A.B两种品牌冰箱月销售量的中位数分别为,;
(2)计算两种品牌月销售量的方差,比较并说明该商场1~5月这两种品牌冰箱月销售量的稳定性.
( http: / / www.21cnjy.com )
20.甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲 8 9 7 9 8 6 7 8 10 8
乙 6 7 9 7 9 10 8 7 7 10
且S乙2=1.8,根据上述信息完成下列问题:
(1)将甲运动员的折线统计图补充完整;
(2)乙运动员射击训练成绩的众数是_____,中位数是______.
(3)求甲运动员射击成绩的平均数和方差,并判断甲、乙两人本次射击成绩的稳定性.
( http: / / www.21cnjy.com )
21.张老师要从班级里数学成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学联赛”为此,他对两位同学进行了辅导,并在辅导期间测验了10次,测验成绩如下表:
第1次 2 3 4 5 6 7 8 9 10
甲 68 80 78 79 78 84 81 83 77 92
乙 86 80 75 83 79 80 85 80 77 75
利用表中数据,解答下列问题:
填空完成下表:
平均成绩 中位数 众数
甲 80
乙 80 80
张老师从测验成绩表中,求得甲的方差,请你计算乙10次测验成绩的方差.
请你根据上面的信息,运用所学统计知识,帮张老师选拔出参加“全国数学联赛”的人选,并简要说明理由.
22.要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.21教育网
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图象,直接比较得出s甲2和s乙2哪个大?
(3)如果其他班级参赛选手 ( http: / / www.21cnjy.com )的射击成绩都在7环左右,本班应该选 参赛更合适;如果其他班级参赛选手的射击成绩都在9环左右,本班应该选 参赛更合适.
( http: / / www.21cnjy.com )
参考答案
1.A
【解析】A、方差越大,数据的波动越大,正确;
B、某种彩票中奖概率为1%,是指买100张彩票可能有1张中奖,错误;
C、旅客上飞机前的安检应采用全面调查,错误;
D、掷一枚硬币,正面不一定朝上,错误,
故选:A.
2.C
【解析】∵方差越小数据组中的数据越稳定,而四名同学这10射击的方差中,最小的是S丙2=0.39,
∴这四人中丙的成绩最稳定.
故选C.
3.D
【解析】A、这组数据中177出现次数最多,即众数为177,此选项正确;
B、这组数据的平均数是:(140+160+169+170×2+177×3+180×2)÷10=170,此选项正确;
C、∵共有10个数,
∴中位数是第5个和6个数的平均数,
∴中位数是(170+177)÷2=173.5;此选项正确;
D、方差=[(140﹣170)2+(160﹣170)2+(169﹣170)2+2×(170﹣170)2+3×(177﹣170)2+2×(180﹣170)2]=134.8;此选项错误;2-1-c-n-j-y
故选:D.
4.B
【解析】试题解析:这组数据按照从小到大的顺序排列为:89,91,91,92,93,96,
则中位数为:,故A错误;
平均数为:,故B正确;
众数为:91,故C错误;
方差S2=
=,故D错误.
故选A.
5.C
【解析】根据方差的公式,可知后面这组数的每个数都比前一个数多2,所以其平均数也比原来的平均数多2,因此根据方差公式可知方差的值变为原来的2×2=8.【来源:21cnj*y.co*m】
故选:C.
6.D
【解析】解:A.∵95>94,∴八(2)班的总分高于八(1)班,不符合题意;
B.∵8.4<12,∴八(2)班的成绩比八(1)班稳定,不符合题意;
C.∵93<94,∴八(2)班的成绩集中在中上游,不符合题意;
D.无法确定两个班的最高分在哪个班,符合题意.
故选D.
点睛:本题主要考查了方差的定义以及算术平均数、中位数、众数,利用表格获取正确的信息是解题的关键.
7.B
【解析】试题解析:设图上的数据从下向上分别为0,1,2,3,4,
∴
根据图可知,图(1)的波动大,图(2)的波动小,∴
故选B.
8.C
【解析】解:由题知,x1+1+x2+1+x3+1+…+xn+1=10n,∴x1+x2+…+xn=10n﹣n=9n
S12=[(x1+1﹣10)2+(x2+1﹣10)2+…+(xn+1﹣10)2]=[(x12+x22+x32+…+xn2)﹣18(x1+x2+x3+…+xn)+81n]=2,∴(x12+x22+x32+…+xn2)=83nwww.21-cn-jy.com
另一组数据的平均数=[x1+2+x2+2+…+xn+2]=[(x1+x2+x3+…+xn)+2n]=[9n+2n]=×11n=11,另一组数据的方差=[(x1+2﹣11)2+(x2+2﹣11)2+…+(xn+2﹣11)2]【出处:21教育名师】
=[(x12+x22+…+xn2)﹣18(x1+x2+…+xn)+81n]=[83n﹣18×9n+81n]=2.故选C.
点睛:本题考查了平均数和方差的定义.实际上数据都同加上一个数方差不变.
9.1.6
【解析】∵,
∴=1.6,
故答案为:1.6.
【点睛】本题考查了方差的计算,熟知方差的求解过程以及方差的计算公式是解题的关键.
10.丙
【解析】由表中数据可知,丙的平均成绩和甲的平均成绩最高,而丙的方差也是最小的,成绩最稳定,所以应该选择:丙.【版权所有:21教育】
故答案为:丙.
11.104
【解析】解:方差S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],其中n是这个样本的容量,x 是样本的平均数,所以本题中这个样本的容量是10,样本的平均数是4.
故答案为:10,4.
12.>
【解析】试题解析:观察平均气温统计图可知:乙地的平均气温比较稳定,波动小;
则乙地的日平均气温的方差小,
故S2甲>S2乙.
故答案为:>.
13.乙
【解析】试题解析:因为0.015<0.026<0.032,即乙的方差<甲的方差<丙的方差,因此射击成绩最稳定的选手是乙.21*cnjy*com
故答案为:乙
14.3
【解析】已知一组数据x1,x2,x3,平均数和方差分别是2,,则另一组数据2x1–1,2x2–1,2x3–1的平均数为=2×2-1=3,方差为4×=.故答案为:3、.
15.x1=x2=…=xn
【解析】根据方差的意义知,方差为0时,这组数据没有波动,即x1=x2=…=xn.
16.(1)见解析(2)选乙厂的产品
【解析】试题分析:(1)平均数就是把这 ( http: / / www.21cnjy.com )组数据加起来的和除以这组数据的总数,再利用方差公式求出即可;
(2)由(1)的结果容易回答,甲厂、乙厂分别利用了平均数、方差进行广告推销,顾客在选购产品时,一般平均数相同,根据方差的大小进行选择.
试题解析:
(1)x甲=×(3+4+5+6+7)=5,
甲=×[(3-5)2+(4-5)2+(5-5)2+(6-5)2+(7-5)2]=2,
x乙=×(4+4+5+6+6)=5,
乙=×[(4-5)2+(4-5)2+(5-5)2+(6-5)2+(6-5)2]=0.8.
(2)由(1)知,甲厂、乙厂的该种电子产品在正常情况下的使用寿命平均数都是5年,
则甲厂方差>乙厂方差,选方差小的厂家的产品,
因此应选乙厂的产品.
17.答案见解析
【解析】试题分析:(1)根据平均数、方差、中位数的概念求值,并填表;(2)根据方差分析稳定性,根据销售趋势看销售前景即可求出答案.
试题解析:
(1)
销售公司 平均数 方差 中位数 众数
甲 9 5.2 9 7
乙 9 17.0 8 8
(2)①甲、乙两个汽车销售公司去年一至十月份的销售平均数一样,都是9辆,但甲销售公司的方差较小,说明甲销售公司的销售情况更稳定。2·1·c·n·j·y
②从甲、乙两个汽车销售公司销售数量的折线图看,乙呈上升趋势,说明乙销售公司较有潜力。
18.(1)众数为14,中位数为15;(2)见解析;(3)可以.
【解析】试题分析:(1)利用加权平均数公式求出平均数,根据众数、中位数的定义即可解决问题;
(2)判断错误.可能抽到13岁,14岁,16岁,17岁;
(3)可以.根据方差公式计算即可;
试题解析:解:(1)平均数==15,众数为14,中位数为15;
(2)判断错误.可能抽到13岁,14岁,16岁,17岁;
(3)可以.
设有n个运动员,则S2= [10% n(13﹣15)2+30% n(14﹣15)2+25% n (15﹣15)2+20% n (16﹣15)2+15% n(17﹣15)2]=1.5.
19.(1)15,15;2;10.4;(2)A品牌更稳定.
【解析】试题分析:(1)根据折线统计图得出A,B两种品牌冰箱的销售台数,即可求出中位数;
(2)先求出A、B的平均数,根据方差公式先求出方差,再将结果比较即可得到结果.
试题解析:(1)A品牌冰箱月销售量从小到大的排列为:13,14,15,16,17,
B品牌冰箱月销售量从小到大排列为:10,14,15,16,20,
∴A品牌冰箱月销售量的中位数为15台,
B品牌冰箱月销售量的中位数为15台,
故答案为:15,15;
(2)=═15(台);
=═15(台);
S2A=[(13 15)2+(14 15)2+(15 15)2+(16 15)2+(17 15)2]÷5=2,21·cn·jy·com
S2B=[(10 15)2+(14 15)2+(15 15)2+(16 15)2+(20 15)2]÷5=10.4;
∵S2A∴A品牌冰箱的月销售量稳定.
20.77.5
【解析】试题分析:(1)根据表格中的数据可以将折线统计图补充完整;
(2)根据表格中的数据可以得到乙运动员射击训练成绩的众数和中位数;
(3)根据表格中的数据可以计算出甲运动员射击成绩的平均数和方差,根据甲乙两人的方差可以得到谁的稳定性好.
试题解析:(1)由表格中的数据可以将折线统计图补充完成,如图所示,
( http: / / www.21cnjy.com )
(2)将乙的射击成绩按照从小到大排列是:
6,7,7,7,7,8,9,9,10,10,
故乙运动员射击训练成绩的众数是7,中位数是:=7.5,
故答案为:7,7.5;
(3)由表格可得,
=8,
=1.2,
∵1.5<1.8,
∴甲本次射击成绩的稳定性好,
即甲运动员射击成绩的平均数是8,方差是1.2,甲本次射击成绩的稳定性好.
21.(1)见解析(2)13(3)乙
【解析】试题分析:(1)首先把乙的数据重新排序,然后根据中位数和众数的定义即可求解;
(2)根据方差计算公式利用表格数据即可求解;
(3)利用方差、中位数、众数的作用即可求解.
试题解析:
解:(1)填空完成下表:
平均成绩 中位数 众数
甲 80 80
乙 80 80 80
(2);
(3)∵,,
∴乙的成绩比较稳定,他们的平均数、中位数、众数几乎没有差别,
∴应该选拔乙去.
点睛:此题主要考查了方差、平均数、 ( http: / / www.21cnjy.com )众数、中位数等统计量,其中方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.【来源:21·世纪·教育·网】
22.(1)乙的平均成绩是8环;(2)s甲2>s乙2;(3)乙,甲.
【解析】分析:(1)根据平均数的计算公式和折线统计图给出的数据即可得出答案;
(2)根据图形波动的大小可直接得出 ( http: / / www.21cnjy.com )答案;(3)根据射击成绩都在7环左右的多少可得出乙参赛更合适;根据射击成绩都在9环左右的多少可得出甲参赛更合适.
本题解析:
(1)乙的平均成绩是:(8+9+8+8+7+8+9+8+8+7)÷10=8(环).
(2)根据图象可知:甲的波动大于乙的波动,则s甲2>s乙2;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选乙参赛更合适;
如果其他班级参赛选手的射击成绩都在9环左右,本班应该选甲参赛更合适.
故答案为:乙,甲.
点睛:本题考查方差的意义,方差是用来衡量一组 ( http: / / www.21cnjy.com )数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.www-2-1-cnjy-com
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
20.3 数据的离散程度同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.(1)方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.
(2)用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况,这个结果叫方差,通常用s2来表示,计算公式是:
s2= [(x1-x )2+(x2-x )2+…+(xn-x )2](可简单记忆为“方差等于差方的平均数”)
(3)方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.21教育名师原创作品
2.求一组数据的平均数、标准差和方差都可以用计算器来计算.
基础知识和能力拓展精练
一、选择题
1.下列说法正确的是( )
A.方差越大,数据的波动越大
B.某种彩票中奖概率为1%,是指买100张彩票一定有1张中奖
C.旅客上飞机前的安检应采用抽样调查
D.掷一枚硬币,正面一定朝上
2.甲、乙、丙、丁四人进行射击测试,每人 ( http: / / www.21cnjy.com )10次射击的平均成绩都为9环,方差分别为S甲2=0.56,S乙2=0.62,S丙2=0.39,S丁2=0.42,则四人中成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
3.2013年安庆市体育考试跳绳项目为学生 ( http: / / www.21cnjy.com )选考项目,下表是某班模拟考试时10名同学的测试成绩(单位:个/分钟),则关于这10名同学每分钟跳绳的测试成绩,下列说法错误的是( )
成绩(个/分钟) 140 160 169 170 177 180
人数 1 1 1 2 3 2
A.众数是177B.平均数是170C.中位数是173.5D.方差是135
4.某数学兴趣小组6名成员通过一次数学竞赛进行组内评比,他们的成绩分别是89,92,91,93,96,91,则关于这组数据说法正确的有( )
A.中位数是92.5 B.平均数是92 C.众数是96 D.方差是5
5.数据1,2,3,4,5的方差为2,则3,5,7,9,11的方差为( )
A.6 B.7 C.8 D.9
6.某校八年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛.各参赛选手成绩的数据分析如下表所示,则以下判断错误的是( )
班级 平均数 中位数 众数 方差
八(1)班 94 93 94 12
八(2)班 95 95.5 93 8.4
A.八(2)班的总分高于八(1)班 B.八(2)班的成绩比八(1)班稳定
C.八(2)班的成绩集中在中上游 D.两个班的最高分在八(2)班
7.两组数据如下图,设图(1)中数据的平均数为 ( http: / / www.21cnjy.com )、方差为 ( http: / / www.21cnjy.com ),图(2)中数据的平均数为 ( http: / / www.21cnjy.com )、方差为 ( http: / / www.21cnjy.com ),则下列关系成立的是( ).21世纪教育网版权所有
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
8.若样本x1+1,x2+1,…,xn+1的平均数为10,方差为2,则对于样本x1+2,x2+2,…,xn+2,下列结论正确的是( )21cnjy.com
A.平均数为10,方差为2 B.平均数为11,方差为3
C.平均数为11,方差为2 D.平均数为12,方差为4
二、填空题
9.数据3,3,6,5,3的方差是_____.
10.下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
方差 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
根据表中数据,要从甲、乙、丙、丁中选择一名成绩好又发挥稳定的运动员参加决赛,应该选择__________.21·世纪*教育网
11.一组数据的方差是,…,则这组数据共有_______个,平均数是________.
12.甲乙两地9月上旬的日平均气温如图所示,则甲乙两地这10天日平均气温方差大小关系为(填>或<).21*cnjy*com
( http: / / www.21cnjy.com )
13.甲、乙、丙三位选手各10次射击成绩的平均数和方差,统计如下表:
选手 甲 乙 丙
平均数 9.3 9.3 9.3
方差 0.026 0.015 0.032
则射击成绩最稳定的选手是________.(填“甲”“乙”“丙”中的一个)
14.已知一组数据x1,x2,x3,平均数和方差分别是2,,那么另一组数据2x1–1,2x2–1,2x3–1的平均数和方差分别是_______,___________.
15.设x1,x2,…,xn平均数为,方差为.若,则x1,x2,…,xn应满足的条件是________________.
三、解答题
16.甲、乙两个电子厂在广告中都声称他们的 ( http: / / www.21cnjy.com )某种电子产品在正常情况下的使用寿命都是5年.质检部门对这两家销售的产品的使用寿命进行了跟踪调查,统计结果如下:(单位:年)
甲厂:3,4,5,6,7 乙厂:4,4,5,6,6
(1)分别求出甲、乙两厂的该种电子产品在正常情况下的使用寿命的平均数和方差;
(2)如果你是顾客,你会选购哪家电子厂的产品?说明理由.
17.某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
(1)请你根据左图填写右表:
销售公司 平均数 方差 中位数 众数
甲 9
乙 9 17.0 8
( http: / / www.21cnjy.com )
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势
看(分析哪个汽车销售公司较有潜力).
18.某射击队为了解运动员的年龄情况,作了一次年龄调查,根据射击运动员的年龄(单位:岁),绘制出如下的统计图.
(1)你能利用该统计图求出平均数、众数和中位数中的哪些统计量?并直接写出结果;
(2)小颖认为,若从该射击队中任意挑选四名队员,则必有一名队员的年龄是15岁.你认为她的判断正确吗?为什么?
(3)小亮认为,可用该统计图求出方差.你认同他的看法吗?若认同,请求出方差;若不认同,请说明理由.
( http: / / www.21cnjy.com )
19.某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图
(1)该商场这段时间内A.B两种品牌冰箱月销售量的中位数分别为,;
(2)计算两种品牌月销售量的方差,比较并说明该商场1~5月这两种品牌冰箱月销售量的稳定性.
( http: / / www.21cnjy.com )
20.甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲 8 9 7 9 8 6 7 8 10 8
乙 6 7 9 7 9 10 8 7 7 10
且S乙2=1.8,根据上述信息完成下列问题:
(1)将甲运动员的折线统计图补充完整;
(2)乙运动员射击训练成绩的众数是_____,中位数是______.
(3)求甲运动员射击成绩的平均数和方差,并判断甲、乙两人本次射击成绩的稳定性.
( http: / / www.21cnjy.com )
21.张老师要从班级里数学成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学联赛”为此,他对两位同学进行了辅导,并在辅导期间测验了10次,测验成绩如下表:
第1次 2 3 4 5 6 7 8 9 10
甲 68 80 78 79 78 84 81 83 77 92
乙 86 80 75 83 79 80 85 80 77 75
利用表中数据,解答下列问题:
填空完成下表:
平均成绩 中位数 众数
甲 80
乙 80 80
张老师从测验成绩表中,求得甲的方差,请你计算乙10次测验成绩的方差.
请你根据上面的信息,运用所学统计知识,帮张老师选拔出参加“全国数学联赛”的人选,并简要说明理由.
22.要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.21教育网
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图象,直接比较得出s甲2和s乙2哪个大?
(3)如果其他班级参赛选手 ( http: / / www.21cnjy.com )的射击成绩都在7环左右,本班应该选 参赛更合适;如果其他班级参赛选手的射击成绩都在9环左右,本班应该选 参赛更合适.
( http: / / www.21cnjy.com )
参考答案
1.A
【解析】A、方差越大,数据的波动越大,正确;
B、某种彩票中奖概率为1%,是指买100张彩票可能有1张中奖,错误;
C、旅客上飞机前的安检应采用全面调查,错误;
D、掷一枚硬币,正面不一定朝上,错误,
故选:A.
2.C
【解析】∵方差越小数据组中的数据越稳定,而四名同学这10射击的方差中,最小的是S丙2=0.39,
∴这四人中丙的成绩最稳定.
故选C.
3.D
【解析】A、这组数据中177出现次数最多,即众数为177,此选项正确;
B、这组数据的平均数是:(140+160+169+170×2+177×3+180×2)÷10=170,此选项正确;
C、∵共有10个数,
∴中位数是第5个和6个数的平均数,
∴中位数是(170+177)÷2=173.5;此选项正确;
D、方差=[(140﹣170)2+(160﹣170)2+(169﹣170)2+2×(170﹣170)2+3×(177﹣170)2+2×(180﹣170)2]=134.8;此选项错误;2-1-c-n-j-y
故选:D.
4.B
【解析】试题解析:这组数据按照从小到大的顺序排列为:89,91,91,92,93,96,
则中位数为:,故A错误;
平均数为:,故B正确;
众数为:91,故C错误;
方差S2=
=,故D错误.
故选A.
5.C
【解析】根据方差的公式,可知后面这组数的每个数都比前一个数多2,所以其平均数也比原来的平均数多2,因此根据方差公式可知方差的值变为原来的2×2=8.【来源:21cnj*y.co*m】
故选:C.
6.D
【解析】解:A.∵95>94,∴八(2)班的总分高于八(1)班,不符合题意;
B.∵8.4<12,∴八(2)班的成绩比八(1)班稳定,不符合题意;
C.∵93<94,∴八(2)班的成绩集中在中上游,不符合题意;
D.无法确定两个班的最高分在哪个班,符合题意.
故选D.
点睛:本题主要考查了方差的定义以及算术平均数、中位数、众数,利用表格获取正确的信息是解题的关键.
7.B
【解析】试题解析:设图上的数据从下向上分别为0,1,2,3,4,
∴
根据图可知,图(1)的波动大,图(2)的波动小,∴
故选B.
8.C
【解析】解:由题知,x1+1+x2+1+x3+1+…+xn+1=10n,∴x1+x2+…+xn=10n﹣n=9n
S12=[(x1+1﹣10)2+(x2+1﹣10)2+…+(xn+1﹣10)2]=[(x12+x22+x32+…+xn2)﹣18(x1+x2+x3+…+xn)+81n]=2,∴(x12+x22+x32+…+xn2)=83nwww.21-cn-jy.com
另一组数据的平均数=[x1+2+x2+2+…+xn+2]=[(x1+x2+x3+…+xn)+2n]=[9n+2n]=×11n=11,另一组数据的方差=[(x1+2﹣11)2+(x2+2﹣11)2+…+(xn+2﹣11)2]【出处:21教育名师】
=[(x12+x22+…+xn2)﹣18(x1+x2+…+xn)+81n]=[83n﹣18×9n+81n]=2.故选C.
点睛:本题考查了平均数和方差的定义.实际上数据都同加上一个数方差不变.
9.1.6
【解析】∵,
∴=1.6,
故答案为:1.6.
【点睛】本题考查了方差的计算,熟知方差的求解过程以及方差的计算公式是解题的关键.
10.丙
【解析】由表中数据可知,丙的平均成绩和甲的平均成绩最高,而丙的方差也是最小的,成绩最稳定,所以应该选择:丙.【版权所有:21教育】
故答案为:丙.
11.104
【解析】解:方差S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],其中n是这个样本的容量,x 是样本的平均数,所以本题中这个样本的容量是10,样本的平均数是4.
故答案为:10,4.
12.>
【解析】试题解析:观察平均气温统计图可知:乙地的平均气温比较稳定,波动小;
则乙地的日平均气温的方差小,
故S2甲>S2乙.
故答案为:>.
13.乙
【解析】试题解析:因为0.015<0.026<0.032,即乙的方差<甲的方差<丙的方差,因此射击成绩最稳定的选手是乙.21*cnjy*com
故答案为:乙
14.3
【解析】已知一组数据x1,x2,x3,平均数和方差分别是2,,则另一组数据2x1–1,2x2–1,2x3–1的平均数为=2×2-1=3,方差为4×=.故答案为:3、.
15.x1=x2=…=xn
【解析】根据方差的意义知,方差为0时,这组数据没有波动,即x1=x2=…=xn.
16.(1)见解析(2)选乙厂的产品
【解析】试题分析:(1)平均数就是把这 ( http: / / www.21cnjy.com )组数据加起来的和除以这组数据的总数,再利用方差公式求出即可;
(2)由(1)的结果容易回答,甲厂、乙厂分别利用了平均数、方差进行广告推销,顾客在选购产品时,一般平均数相同,根据方差的大小进行选择.
试题解析:
(1)x甲=×(3+4+5+6+7)=5,
甲=×[(3-5)2+(4-5)2+(5-5)2+(6-5)2+(7-5)2]=2,
x乙=×(4+4+5+6+6)=5,
乙=×[(4-5)2+(4-5)2+(5-5)2+(6-5)2+(6-5)2]=0.8.
(2)由(1)知,甲厂、乙厂的该种电子产品在正常情况下的使用寿命平均数都是5年,
则甲厂方差>乙厂方差,选方差小的厂家的产品,
因此应选乙厂的产品.
17.答案见解析
【解析】试题分析:(1)根据平均数、方差、中位数的概念求值,并填表;(2)根据方差分析稳定性,根据销售趋势看销售前景即可求出答案.
试题解析:
(1)
销售公司 平均数 方差 中位数 众数
甲 9 5.2 9 7
乙 9 17.0 8 8
(2)①甲、乙两个汽车销售公司去年一至十月份的销售平均数一样,都是9辆,但甲销售公司的方差较小,说明甲销售公司的销售情况更稳定。2·1·c·n·j·y
②从甲、乙两个汽车销售公司销售数量的折线图看,乙呈上升趋势,说明乙销售公司较有潜力。
18.(1)众数为14,中位数为15;(2)见解析;(3)可以.
【解析】试题分析:(1)利用加权平均数公式求出平均数,根据众数、中位数的定义即可解决问题;
(2)判断错误.可能抽到13岁,14岁,16岁,17岁;
(3)可以.根据方差公式计算即可;
试题解析:解:(1)平均数==15,众数为14,中位数为15;
(2)判断错误.可能抽到13岁,14岁,16岁,17岁;
(3)可以.
设有n个运动员,则S2= [10% n(13﹣15)2+30% n(14﹣15)2+25% n (15﹣15)2+20% n (16﹣15)2+15% n(17﹣15)2]=1.5.
19.(1)15,15;2;10.4;(2)A品牌更稳定.
【解析】试题分析:(1)根据折线统计图得出A,B两种品牌冰箱的销售台数,即可求出中位数;
(2)先求出A、B的平均数,根据方差公式先求出方差,再将结果比较即可得到结果.
试题解析:(1)A品牌冰箱月销售量从小到大的排列为:13,14,15,16,17,
B品牌冰箱月销售量从小到大排列为:10,14,15,16,20,
∴A品牌冰箱月销售量的中位数为15台,
B品牌冰箱月销售量的中位数为15台,
故答案为:15,15;
(2)=═15(台);
=═15(台);
S2A=[(13 15)2+(14 15)2+(15 15)2+(16 15)2+(17 15)2]÷5=2,21·cn·jy·com
S2B=[(10 15)2+(14 15)2+(15 15)2+(16 15)2+(20 15)2]÷5=10.4;
∵S2A
20.77.5
【解析】试题分析:(1)根据表格中的数据可以将折线统计图补充完整;
(2)根据表格中的数据可以得到乙运动员射击训练成绩的众数和中位数;
(3)根据表格中的数据可以计算出甲运动员射击成绩的平均数和方差,根据甲乙两人的方差可以得到谁的稳定性好.
试题解析:(1)由表格中的数据可以将折线统计图补充完成,如图所示,
( http: / / www.21cnjy.com )
(2)将乙的射击成绩按照从小到大排列是:
6,7,7,7,7,8,9,9,10,10,
故乙运动员射击训练成绩的众数是7,中位数是:=7.5,
故答案为:7,7.5;
(3)由表格可得,
=8,
=1.2,
∵1.5<1.8,
∴甲本次射击成绩的稳定性好,
即甲运动员射击成绩的平均数是8,方差是1.2,甲本次射击成绩的稳定性好.
21.(1)见解析(2)13(3)乙
【解析】试题分析:(1)首先把乙的数据重新排序,然后根据中位数和众数的定义即可求解;
(2)根据方差计算公式利用表格数据即可求解;
(3)利用方差、中位数、众数的作用即可求解.
试题解析:
解:(1)填空完成下表:
平均成绩 中位数 众数
甲 80 80
乙 80 80 80
(2);
(3)∵,,
∴乙的成绩比较稳定,他们的平均数、中位数、众数几乎没有差别,
∴应该选拔乙去.
点睛:此题主要考查了方差、平均数、 ( http: / / www.21cnjy.com )众数、中位数等统计量,其中方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.【来源:21·世纪·教育·网】
22.(1)乙的平均成绩是8环;(2)s甲2>s乙2;(3)乙,甲.
【解析】分析:(1)根据平均数的计算公式和折线统计图给出的数据即可得出答案;
(2)根据图形波动的大小可直接得出 ( http: / / www.21cnjy.com )答案;(3)根据射击成绩都在7环左右的多少可得出乙参赛更合适;根据射击成绩都在9环左右的多少可得出甲参赛更合适.
本题解析:
(1)乙的平均成绩是:(8+9+8+8+7+8+9+8+8+7)÷10=8(环).
(2)根据图象可知:甲的波动大于乙的波动,则s甲2>s乙2;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选乙参赛更合适;
如果其他班级参赛选手的射击成绩都在9环左右,本班应该选甲参赛更合适.
故答案为:乙,甲.
点睛:本题考查方差的意义,方差是用来衡量一组 ( http: / / www.21cnjy.com )数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.www-2-1-cnjy-com
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
