第十章 数据的收集、整理与描述单元检测试卷(含解析)
文档属性
| 名称 | 第十章 数据的收集、整理与描述单元检测试卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 578.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-25 00:00:00 | ||
图片预览

文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
第十章 数据的收集、整理与描述单元检测试卷
班级__________姓名____________总分___________
一、选择题
1.下面数据用扇形统计图较合适的是( )
A. 本班学生的年龄统计
B. 本班学生一年来的身高变化统计
C. 本班学生参加各种活动小组的比例统计
D. 本班学生穿鞋型号的统计
2.某学校教研组对八年级360名学生就“分组合作学习”方式的支持程度进行了调查,随机抽取了若干名学生进行调查,并制作统计图,据此统计图估计该校八年级支持“分组合作学习”方式的学生约为(含非常喜欢和喜欢两种情况)( )
A. 216 B. 252 C. 288 D. 324
3.下列调查中,适合用抽样调查的是 ( )
A.了解报考军事院校考生的视力 B.旅客上飞机前的安检
C.对招聘教师中的应聘人员进行面试 D.了解全市中小学生每天的零花钱
4.某校初三(1)班有同学50人,他们对球类运动的喜欢用图所示的统计图来表示,那么喜欢足球的人数是( )
A、 40人 B、30人 C、 20人 D、 10人
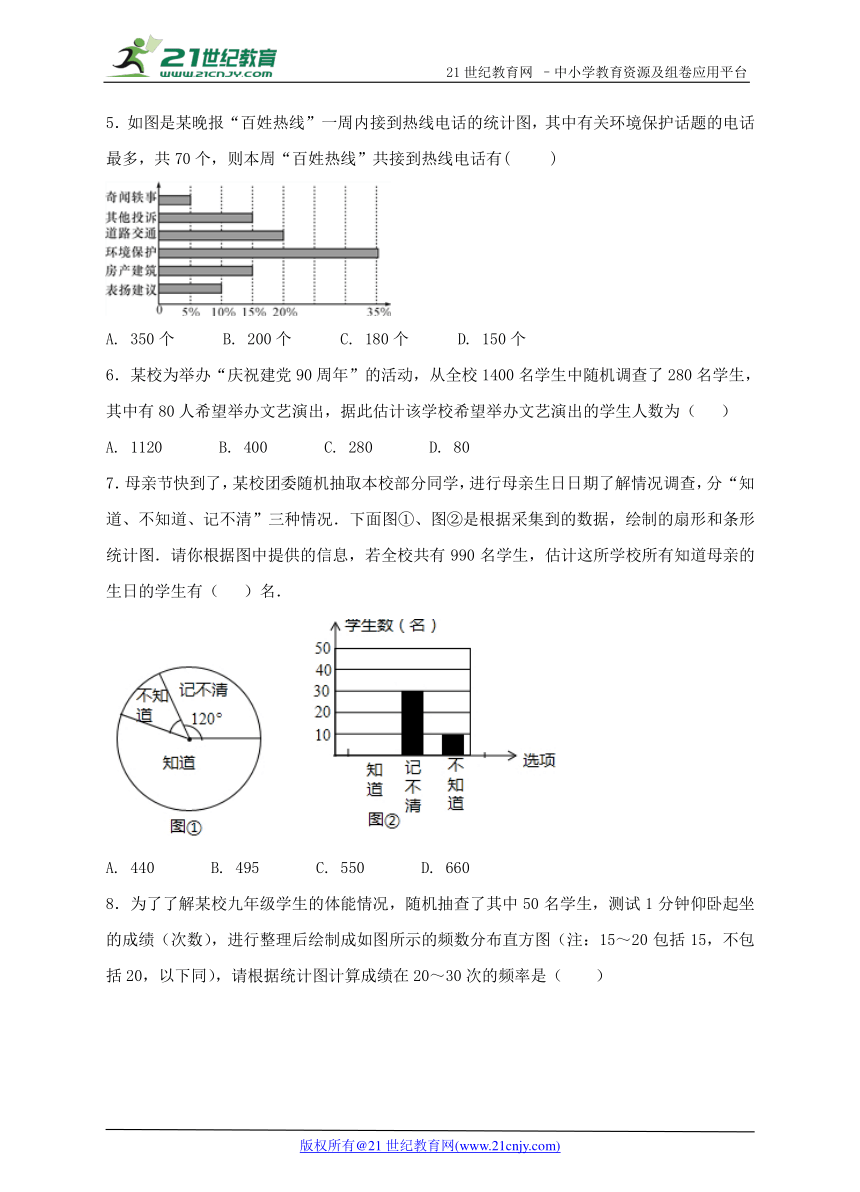
5.如图是某晚报“百姓热线”一周内接到热线电话的统计图,其中有关环境保护话题的电话最多,共70个,则本周“百姓热线”共接到热线电话有( )
A. 350个 B. 200个 C. 180个 D. 150个
6.某校为举办“庆祝建党90周年”的活动,从全校1400名学生中随机调查了280名学生,其中有80人希望举办文艺演出,据此估计该学校希望举办文艺演出的学生人数为( )
A. 1120 B. 400 C. 280 D. 80
7.母亲节快到了,某校团委随机抽取本校部分同学,进行母亲生日日期了解情况调查,分“知道、不知道、记不清”三种情况.下面图①、图②是根据采集到的数据,绘制的扇形和条形统计图.请你根据图中提供的信息,若全校共有990名学生,估计这所学校所有知道母亲的生日的学生有( )名.
A. 440 B. 495 C. 550 D. 660
8.为了了解某校九年级学生的体能情况,随机抽查了其中50名学生,测试1分钟仰卧起坐的成绩(次数),进行整理后绘制成如图所示的频数分布直方图(注:15~20包括15,不包括20,以下同),请根据统计图计算成绩在20~30次的频率是( )
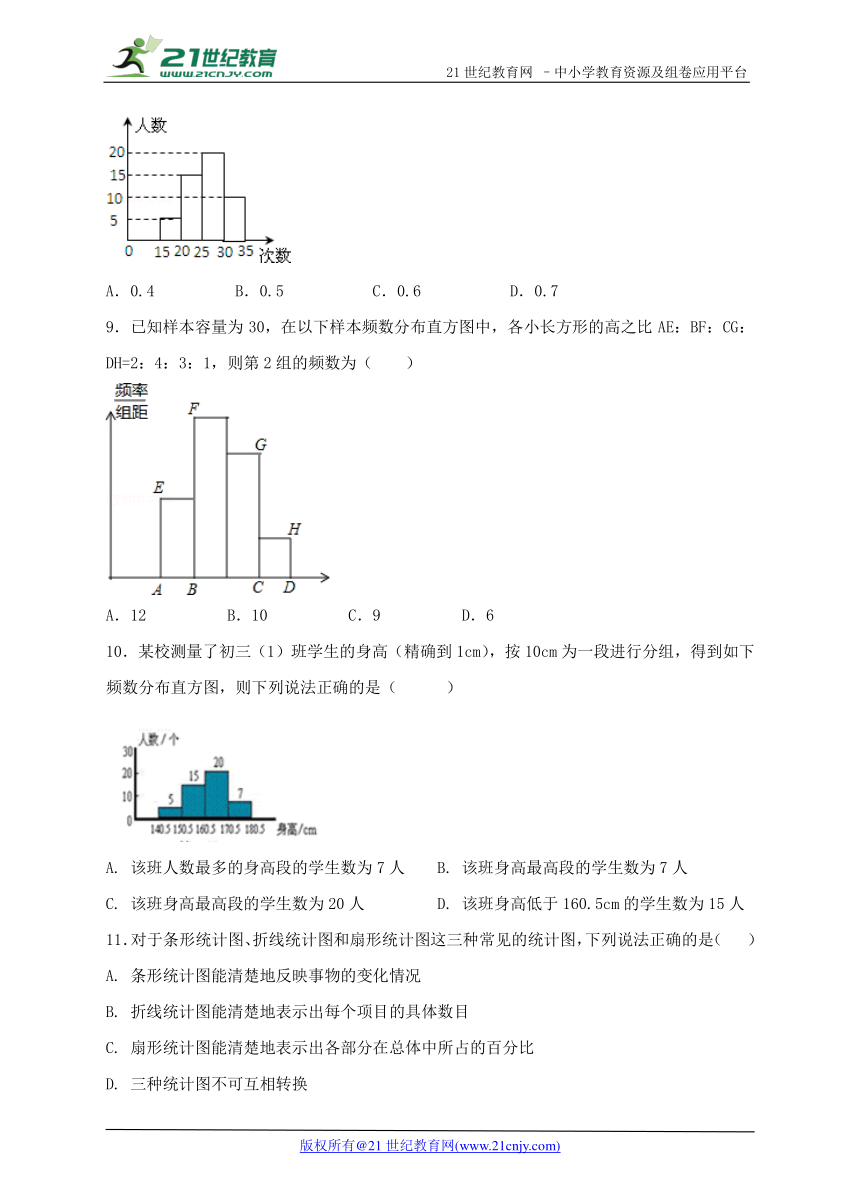
A.0.4 B.0.5 C.0.6 D.0.7
9.已知样本容量为30,在以下样本频数分布直方图中,各小长方形的高之比AE:BF:CG:DH=2:4:3:1,则第2组的频数为( )
A.12 B.10 C.9 D.6
10.某校测量了初三(1)班学生的身高(精确到1cm),按10cm为一段进行分组,得到如下频数分布直方图,则下列说法正确的是( )
A. 该班人数最多的身高段的学生数为7人 B. 该班身高最高段的学生数为7人
C. 该班身高最高段的学生数为20人 D. 该班身高低于160.5cm的学生数为15人
11.对于条形统计图、折线统计图和扇形统计图这三种常见的统计图,下列说法正确的是( )
A. 条形统计图能清楚地反映事物的变化情况
B. 折线统计图能清楚地表示出每个项目的具体数目
C. 扇形统计图能清楚地表示出各部分在总体中所占的百分比
D. 三种统计图不可互相转换
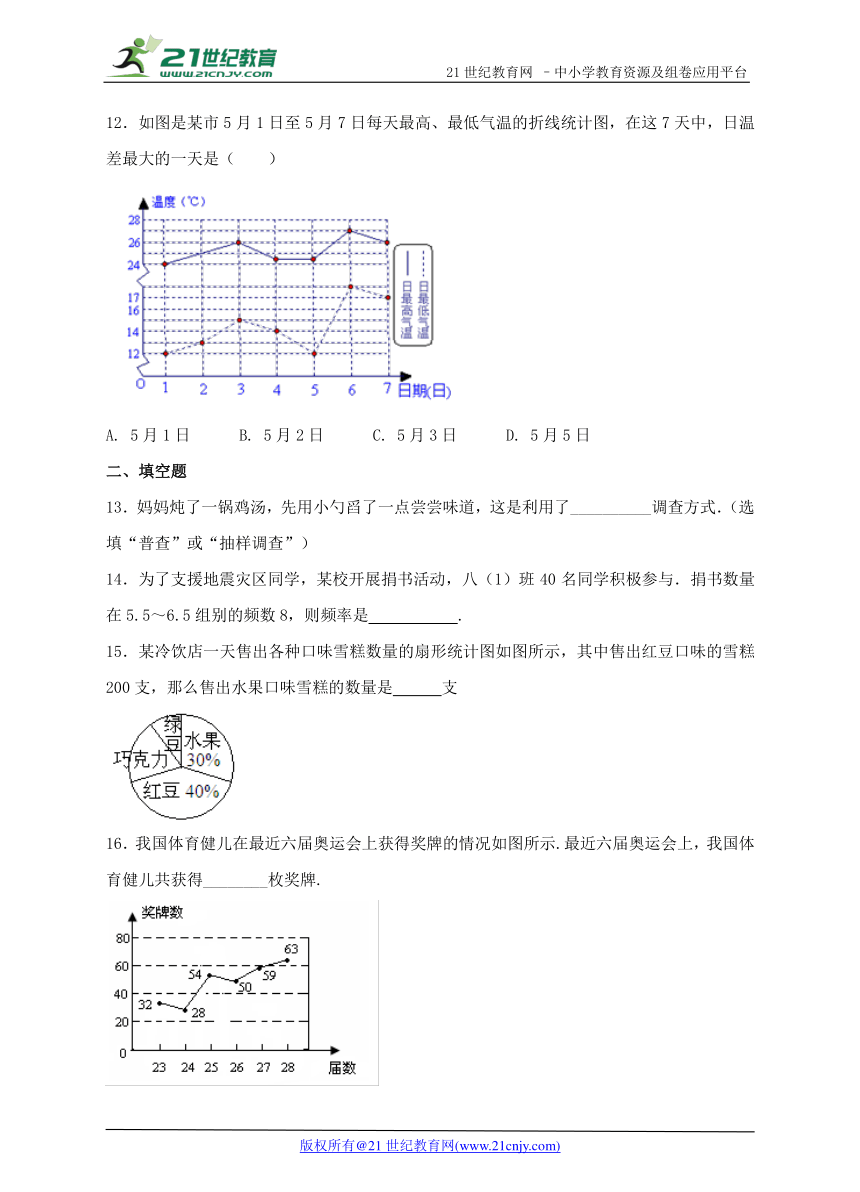
12.如图是某市5月1日至5月7日每天最高、最低气温的折线统计图,在这7天中,日温差最大的一天是( )
A. 5月1日 B. 5月2日 C. 5月3日 D. 5月5日
二、填空题
13.妈妈炖了一锅鸡汤,先用小勺舀了一点尝尝味道,这是利用了__________调查方式.(选填“普查”或“抽样调查”)
14.为了支援地震灾区同学,某校开展捐书活动,八(1)班40名同学积极参与.捐书数量在5.5~6.5组别的频数8,则频率是 .
15.某冷饮店一天售出各种口味雪糕数量的扇形统计图如图所示,其中售出红豆口味的雪糕200支,那么售出水果口味雪糕的数量是 支
16.我国体育健儿在最近六届奥运会上获得奖牌的情况如图所示.最近六届奥运会上,我国体育健儿共获得________枚奖牌.
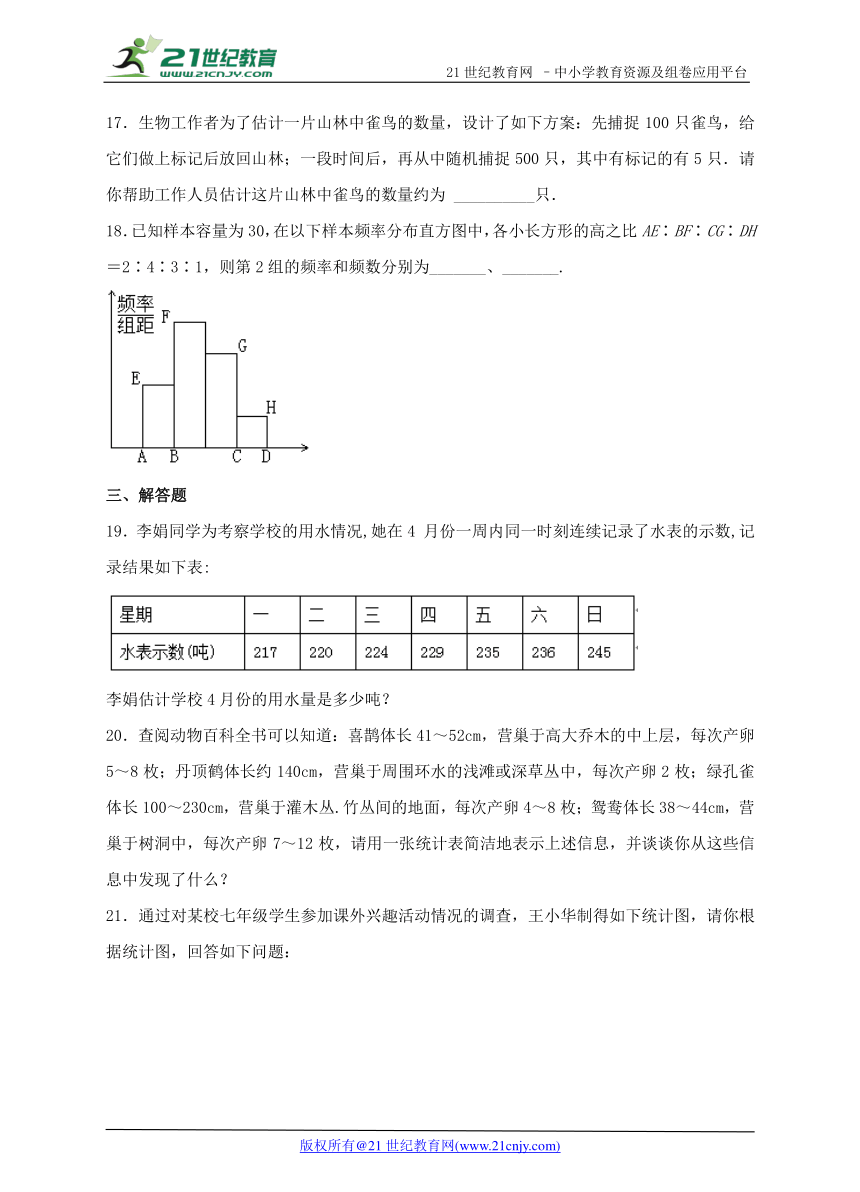
17.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉100只雀鸟,给它们做上标记后放回山林;一段时间后,再从中随机捕捉500只,其中有标记的有5只.请你帮助工作人员估计这片山林中雀鸟的数量约为 __________只.
18.已知样本容量为30,在以下样本频率分布直方图中,各小长方形的高之比AE∶BF∶CG∶DH=2∶4∶3∶1,则第2组的频率和频数分别为_______、_______.
三、解答题
19.李娟同学为考察学校的用水情况,她在4 月份一周内同一时刻连续记录了水表的示数,记录结果如下表:
李娟估计学校4月份的用水量是多少吨?
20.查阅动物百科全书可以知道:喜鹊体长41~52cm,营巢于高大乔木的中上层,每次产卵5~8枚;丹顶鹤体长约140cm,营巢于周围环水的浅滩或深草丛中,每次产卵2枚;绿孔雀体长100~230cm,营巢于灌木丛.竹丛间的地面,每次产卵4~8枚;鸳鸯体长38~44cm,营巢于树洞中,每次产卵7~12枚,请用一张统计表简洁地表示上述信息,并谈谈你从这些信息中发现了什么?
21.通过对某校七年级学生参加课外兴趣活动情况的调查,王小华制得如下统计图,请你根据统计图,回答如下问题:
(1)哪种课外活动小组最受欢迎?
(2)哪两种课外活动小组的受欢迎程度较为接近?
(3)你还能从该统计图中获得其它信息吗?
(4)你能从统计图中计算出参加各个课外活动小组的人数吗?如果能,请计算出来.
22.(本题8分)某县八年级有3000名学生参加“爱我中华知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中随机抽取了部分学生的得分进行统计.请你根据不完整的表格,解答下列问题:
成绩 x 分 频 数 频 率
50≤x<60 10
60≤ x <70 16 0.08
70≤ x <80 0.2
80≤ x <90 62 0.31
90≤ x <100 72 0.36
(1)补全频数分布表;
(2)随机抽取的样本容量为 ;
(3)若将得分转化为等级,规定50≤x<60评为“D”,60≤x<70评为“C”,70≤x<90评为“B”,90≤x<100评为“A”.估计这3000名学生中,有多少学生得分等级为A?
23.一个不透明的口袋装有若干个红、黄、蓝、绿四种颜色的小球,小球除颜色外完全相同,为估计该口袋中四种颜色的小球数量,每次从口袋中随机摸出一球记下颜色并放回,重复多次试验,汇总实验结果绘制如图不完整的条形统计图和扇形统计图.
根据以上信息解答下列问题:
(1)求实验总次数,并补全条形统计图;
(2)扇形统计图中,摸到黄色小球次数所在扇形的圆心角度数为多少度?
(3)已知该口袋中有10个红球,请你根据实验结果估计口袋中绿球的数量.
24.为了丰富校园文化生活,某校计划在午间校园广播台播放“百家讲坛”的部分内容.为了了解学生的喜好,抽取若干名学生进行问卷调查(每人只选一项内容),整理调查结果,绘制统计图如下:
请根据统计图提供的信息回答以下问题:
(1)抽取的学生数为____名;
(2)该校有3000名学生,估计喜欢收听易中天《品三国》的学生有____名;
(3)估计该校女学生喜欢收听刘心武评《红楼梦》的约占全校学生的____%;
(4)你认为上述估计合理吗?理由是什么?
25.利群商厦对销量较大的A、B、C三种品牌的纯牛奶进行了问卷调查,共发放问卷300份(问卷由单选和多选题组成),对收回的265份问卷进行了整理,部分数据如下:
(1)最近一次购买各品牌纯牛奶用户比例如图:
(2)用户对各品牌纯牛奶满意情况汇总如下表:
结合上述信息回答下列问题:
①A品牌牛奶的主要竞争优势是什么?请简要说明理由.
②广告对用户选择品牌有影响吗?请简要说明理由.
③你对厂家C有何建议?
26.为了了解我市中学生跳绳活动开展的情况,随机抽查了全市八年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制成如下的两个不完整的统计图:
请根据图中提供的信息,解答下列问题:
(1)本次共抽查了多少名学生?
(2)请补全频数分布直方图;
(3)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生的成绩为优秀;
(4)请你根据以上信息,对我市开展的学生跳绳活动情况谈谈自己的看法或建议.
参考答案
1.C
【解析】根据统计图的特点可知:
A. 本班学生的年龄统计,用条形统计图统计较合适;
B. 本班学生一年来的身高变化统计用折线统计图较合适;
C. 本班学生同时参加各种活动小组的比例统计,用扇形统计图较合适;
D. 本班学生穿鞋型号的统计,用条形统计图较合适;
故选:C.
点睛:此题考查了统计图的选择,条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.
2.B
【解析】试题解析根据题意得:360× EMBED Equation.DSMT4 =252(人),
答:该校八年级支持“分组合作学习”方式的学生约为252人;
故选B.
3.D
【解析】
试题分析:根据题意知了解报考军事院校考生的视力需要全面调查,故A错误;旅客上飞机前的安检需进行全面调查,故B错误;对招聘教师中的应聘人员进行面试需要全面调查,故C错误;了解全市中小学生每天的零花钱则适合抽样调查,故D正确.
故选D
考点:全面调查与抽样调查
4.C
【解析】
试题分析:根据统计图,喜欢足球所占的百比列=1-25%-15%-20%=40%,初三(1)班有同学50人,所以喜欢足球的人数==20
考点:统计
点评:本题考查统计,要求考生能识别统计图,能从统计图中得出对解答本题有用的信息来,本题难度不大
5.B
【解析】由题意可知,环境保护占“百姓热线”共接到热线电话总数的35%,
所以接到电话总数为:70÷35%=200个,
故选:B.
6.B
【解析】试题分析:先求出在随机调查的280名学生中希望举办文艺演出的学生所占的百分比,再用全校的人数乘以这个百分比数即可得到答案.
解:由题意知从全校1400名学生中随机调查了280名学生,其中有80人希望举办文艺演出,
∴希望举办文艺演出的学生所占的百分比为:80÷280=,
∴该学校希望举办文艺演出的学生人数为:1400×=400人.
故选B.
点评:本题考查了用样本估计总体的知识,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.
7.C
【解析】试题解析:调查的总人数:30÷ EMBED Equation.DSMT4 =90,
知道母亲的生日的学生数;90-10-30=50,
这所学校所有知道母亲的生日的学生:990×=550,
故选C.
考点:1.用样本估计总体;2.扇形统计图;3.条形统计图.
8.D
【解析】
试题分析:(15+20)÷(5+10+15+20)=0.7,
故选:D.
考点:频数(率)分布直方图
9.A.
【解析】
试题分析:读图可知:各小长方形的高之比AE:BF:CG:DH=2:4:3:1,即各组频数之比2:4:3:1,
则第2组的频数为×30=12,
故选A.
考点:频数(率)分布直方图.
10.B
【解析】试题分析:正确读取频数分布直方图的信息即可得出答案.
如图所示各阶段身高的人数分别为:[140.5,150.5]5人,[150.5,160.5]15人,[160.5,170.5]20人,[170.5,180.5]7人.所以,该班人数最多的身高段的学生数应为20人,A选项错误;该班身高最高段的学生数为7人,B选项正确C选项错误;该班身高低于160.5cm的学生数为:5+15="20" (人),D选项错误.
考点:直方图.
11.C
【解析】试题解析:A、条形统计图能清楚地表示出每个项目的数据,故此选项错误;
B、折线统计图能清楚地反映事物的变化情况,故此选项错误;
C、扇形统计图直接反映部分占总体的百分比大小,故此选项正确;
D、这三种统计图可以互相转化,但是各有利弊,不是经常互相转化,故此选项错误.
故选C.
点睛:本题考查的是条形统计图和扇形统计图、折线统计图的不同,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小,折线统计图能清楚地反映事物的变化情况.
12.D
【解析】试题解析:在图中,从5月1日至5月7日找出实线与虚线差距最大的一天,为5月5日;
故选D.
13.抽样调查
【解析】试题解析:为了尝味道,应采用的合适的调查方式为抽样调查,
故答案为:抽样调查.
14.0.2.
【解析】
试题分析:根据频率=即可求解.
试题解析:频率==0.2.
考点:频数与频率.
15.150
【解析】
试题分析:由图可知:售出红豆口味的雪糕200支,占40%,
∴售出雪糕总量为200÷40%=500支,
∵水果口味的占30%,
∴水果口味的有500×30%=150支,
故答案为150.考点:统计初步
16.286
【解析】试题解析:奖牌数量为:32+28+54+50+59+63=286(枚).
故答案为:286.
17.10000
【解析】由题意可知:重新捕获500只,其中带标记的有5只,可以知道,在样本中,有标记的占到.而在总体中,有标记的共有100只,根据比例即可解答.
解:100=10000只.
故答案为:10000.
18. 0.4 12
【解析】试题解析:读图可知:各小长方形的高之比AE:BF:CG:DH=2:4:3:1,即各组频数之比2:4:3:1,
则第2组的频数为×30=12,其频率为=0.4.
故本题答案为:0.4;12.
19.140吨
【解析】试题分析:水表显示了七天的数据,但实际上是调查了六天的用水情况.用这六天的用水平均值估计本月的即可.
试题解析:从表中可以看出这6天的平均用水量是吨,
4月份的用水量是=140吨.
20.统计表如下
鸟 名 喜鹊 丹顶鹤 绿孔雀 鸳鸯
营巢环境 大乔木 浅滩.深草丛 灌木丛.竹丛间 树洞
体长(cm) 41~52cm 约140cm 100~230 cm 38~44cm
产卵枚数 5~8 2 4~8 7~12
从统计表可以看出:(1)丹顶鹤和其他三种鸟相比,它的营巢环境要求比较高,而产卵数量比较少,这些可能是丹顶鹤被列为国家一级保护动物的部分原因;(2)鸟类的体长与产卵数量没有明显的关系,等等.
【解析】
试题分析:仔细分析题意即可得到统计表,再根据统计表中的信息即可发现结论.
统计表如下
鸟 名 喜鹊 丹顶鹤 绿孔雀 鸳鸯
营巢环境 大乔木 浅滩.深草丛 灌木丛.竹丛间 树洞
体长(cm) 41~52cm 约140cm 100~230 cm 38~44cm
产卵枚数 5~8 2 4~8 7~12
从统计表可以看出:(1)丹顶鹤和其他三种鸟相比,它的营巢环境要求比较高,而产卵数量比较少,这些可能是丹顶鹤被列为国家一级保护动物的部分原因;(2)鸟类的体长与产卵数量没有明显的关系,等等.
考点:统计表的制作,从统计表中获取信息的能力
点评:本题是统计表的基础应用题,难度一般,学生需认识到统计表可以将大量数据的分类结果清晰、一目了然地表达出来.
21.(1)文艺小组;(2)美术小组与科技小组;(3)答案不唯一;(4)不能
【解析】试题分析:(1)--(3)小问根据扇形统计图所给比例即可求解;
(4)不知学生总数,故无法求解.
试题解析:(1)文艺小组是最受欢迎的课外活动小组,因为它所占的百分比最高.
(2)美术小组与科技小组所占人数的百分比分别为28%和25%,所以这两个课外活动小组的受欢迎程度较为接近.
(3)答案不唯一,如:书法小组参加的人数较少,应该鼓励其他人参加,等.
(4)不能.不知参加课外活动的总人数,也不知任何一个小组的人数.
22.(1)40,0.05 (2)200 (3)1080名
【解析】
试题分析:(1)找出样本中评为“D”的百分比,估计出总体中“D”的人数即可;根据频率和总量的关系,求出70≤x<80分数段的频数;
(2)根据其中已知的频数和频率,可根据总频数=频数÷频率,求得样本容量;
(3)求出等级为A的频率可以求出等级为A的人数.
试题解析:解:(1)70≤x<80分数段的频数40(人),
50≤x<60分数段频率为0.05;
(2)200
(3)根据题意得:3000×0.36=1080,
所以这3000名学生中,有1080名学生得分等级为A.
考点:频率,频数,样本容量,概率
23.(1)200,作图见解析;(2)144°;(3)2.
【解析】试题分析:(1)用摸到红色球的次数除以占的百分比即是实验总次数,用总次数减去红黄绿球的次数即为摸蓝球的次数,再补全条形统计图即可;
(2)用摸到黄色小球次数除以实验总次数,再乘以360°即可得摸到黄色小球次数所在扇形的圆心角度数;
(3)先得出摸到绿色小球次数所占的百分比,再用口袋中有10个红球除以红球所占的百分比得出口袋中小球的总数,最后乘以绿色小球所占的百分比即可.
解:(1)50÷25%=200(次),
所以实验总次数为200次,
条形统计图如下:
(2)=144°;
(3)10÷25%×=2(个),
答:口袋中绿球有2个.
考点:条形统计图;扇形统计图;模拟实验.
24.1.300;2.1060;3.15.4.合理.
【解析】试题分析:(1)男女生所有人数之和;
(2)求出抽取的样本中收听品三国的学生所占的比例,乘3000即可求解;
(3)听红楼梦的女生人数除以总人数.
试题解析:(1)20+10+30+15+30+38+64+42+6+45=300人;
(2) EMBED Equation.DSMT4 ×3000=1060人;
(3)样本中校女学生喜欢收听刘心武评《红楼梦》的约占样本容量的百分比为45÷300=15%,
则该校女学生喜欢收听刘心武评《红楼梦》的约占全校学生的15%;
(4)合理.理由中体现用样本估计总体即可.
考点:1.条形统计图;2.用样本估计总体.
25.(1)理由见解析;(2)理由见解析;(3)建议见解析.
【解析】试题分析:(1)结合统计图表,从购买量、质量、广告、价格等方面进行分析即可;
(2)结合图表中反映的例子进行分析即可;
(3)从厂家C的劣势进行建议即可.
试题解析:(1)A品牌牛奶的主要竞争优势是质量好,因为对此品牌牛奶的质量满意的用户最多,而对其广告、价格满意的用户不是最多。
(2)广告对用户选择品牌有影响,因为对于B、C两种品牌的纯牛奶在质量和价格上顾客满意率是相同的,但由于B品牌牛奶广告做得好,所以销量比C品牌大。
(3)厂家C在提高质量和降低价格的同时,加大宣传力度,重视广告效用。
26.(1) 200名;(2) 图形见解析;(3) 4200名;(4)见解析.
【解析】试题分析:(1)利用95≤x<115的人数是8+16=24人,所占的比例是12%即可求解;
(2)求得范围是115≤x<145的人数,扇形的圆心角度数是360度乘以对应的比例即可求解;
(3)首先求得所占的比例,然后乘以总人数8000即可求解;
(4)根据实际情况,提出自己的见解即可,答案不唯一.
试题解析:(1)(16+8)÷12%=200(名)
(2)范围是135≤x<145的人数是:200-8-16-71-60-16=29(人),
则跳绳次数范围135≤x<155所在扇形的圆心角度数是:360×=81°.
;
(3)优秀的比例是:×100%=52.5%,
则估计全市8000名八年级学生中有多少名学生的成绩为优秀人数是:8000×52.5%=4200(人);
(4)全市达到优秀的人数有一半以上,反映了我市学生锻炼情况很好.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
第十章 数据的收集、整理与描述单元检测试卷
班级__________姓名____________总分___________
一、选择题
1.下面数据用扇形统计图较合适的是( )
A. 本班学生的年龄统计
B. 本班学生一年来的身高变化统计
C. 本班学生参加各种活动小组的比例统计
D. 本班学生穿鞋型号的统计
2.某学校教研组对八年级360名学生就“分组合作学习”方式的支持程度进行了调查,随机抽取了若干名学生进行调查,并制作统计图,据此统计图估计该校八年级支持“分组合作学习”方式的学生约为(含非常喜欢和喜欢两种情况)( )
A. 216 B. 252 C. 288 D. 324
3.下列调查中,适合用抽样调查的是 ( )
A.了解报考军事院校考生的视力 B.旅客上飞机前的安检
C.对招聘教师中的应聘人员进行面试 D.了解全市中小学生每天的零花钱
4.某校初三(1)班有同学50人,他们对球类运动的喜欢用图所示的统计图来表示,那么喜欢足球的人数是( )
A、 40人 B、30人 C、 20人 D、 10人
5.如图是某晚报“百姓热线”一周内接到热线电话的统计图,其中有关环境保护话题的电话最多,共70个,则本周“百姓热线”共接到热线电话有( )
A. 350个 B. 200个 C. 180个 D. 150个
6.某校为举办“庆祝建党90周年”的活动,从全校1400名学生中随机调查了280名学生,其中有80人希望举办文艺演出,据此估计该学校希望举办文艺演出的学生人数为( )
A. 1120 B. 400 C. 280 D. 80
7.母亲节快到了,某校团委随机抽取本校部分同学,进行母亲生日日期了解情况调查,分“知道、不知道、记不清”三种情况.下面图①、图②是根据采集到的数据,绘制的扇形和条形统计图.请你根据图中提供的信息,若全校共有990名学生,估计这所学校所有知道母亲的生日的学生有( )名.
A. 440 B. 495 C. 550 D. 660
8.为了了解某校九年级学生的体能情况,随机抽查了其中50名学生,测试1分钟仰卧起坐的成绩(次数),进行整理后绘制成如图所示的频数分布直方图(注:15~20包括15,不包括20,以下同),请根据统计图计算成绩在20~30次的频率是( )
A.0.4 B.0.5 C.0.6 D.0.7
9.已知样本容量为30,在以下样本频数分布直方图中,各小长方形的高之比AE:BF:CG:DH=2:4:3:1,则第2组的频数为( )
A.12 B.10 C.9 D.6
10.某校测量了初三(1)班学生的身高(精确到1cm),按10cm为一段进行分组,得到如下频数分布直方图,则下列说法正确的是( )
A. 该班人数最多的身高段的学生数为7人 B. 该班身高最高段的学生数为7人
C. 该班身高最高段的学生数为20人 D. 该班身高低于160.5cm的学生数为15人
11.对于条形统计图、折线统计图和扇形统计图这三种常见的统计图,下列说法正确的是( )
A. 条形统计图能清楚地反映事物的变化情况
B. 折线统计图能清楚地表示出每个项目的具体数目
C. 扇形统计图能清楚地表示出各部分在总体中所占的百分比
D. 三种统计图不可互相转换
12.如图是某市5月1日至5月7日每天最高、最低气温的折线统计图,在这7天中,日温差最大的一天是( )
A. 5月1日 B. 5月2日 C. 5月3日 D. 5月5日
二、填空题
13.妈妈炖了一锅鸡汤,先用小勺舀了一点尝尝味道,这是利用了__________调查方式.(选填“普查”或“抽样调查”)
14.为了支援地震灾区同学,某校开展捐书活动,八(1)班40名同学积极参与.捐书数量在5.5~6.5组别的频数8,则频率是 .
15.某冷饮店一天售出各种口味雪糕数量的扇形统计图如图所示,其中售出红豆口味的雪糕200支,那么售出水果口味雪糕的数量是 支
16.我国体育健儿在最近六届奥运会上获得奖牌的情况如图所示.最近六届奥运会上,我国体育健儿共获得________枚奖牌.
17.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉100只雀鸟,给它们做上标记后放回山林;一段时间后,再从中随机捕捉500只,其中有标记的有5只.请你帮助工作人员估计这片山林中雀鸟的数量约为 __________只.
18.已知样本容量为30,在以下样本频率分布直方图中,各小长方形的高之比AE∶BF∶CG∶DH=2∶4∶3∶1,则第2组的频率和频数分别为_______、_______.
三、解答题
19.李娟同学为考察学校的用水情况,她在4 月份一周内同一时刻连续记录了水表的示数,记录结果如下表:
李娟估计学校4月份的用水量是多少吨?
20.查阅动物百科全书可以知道:喜鹊体长41~52cm,营巢于高大乔木的中上层,每次产卵5~8枚;丹顶鹤体长约140cm,营巢于周围环水的浅滩或深草丛中,每次产卵2枚;绿孔雀体长100~230cm,营巢于灌木丛.竹丛间的地面,每次产卵4~8枚;鸳鸯体长38~44cm,营巢于树洞中,每次产卵7~12枚,请用一张统计表简洁地表示上述信息,并谈谈你从这些信息中发现了什么?
21.通过对某校七年级学生参加课外兴趣活动情况的调查,王小华制得如下统计图,请你根据统计图,回答如下问题:
(1)哪种课外活动小组最受欢迎?
(2)哪两种课外活动小组的受欢迎程度较为接近?
(3)你还能从该统计图中获得其它信息吗?
(4)你能从统计图中计算出参加各个课外活动小组的人数吗?如果能,请计算出来.
22.(本题8分)某县八年级有3000名学生参加“爱我中华知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中随机抽取了部分学生的得分进行统计.请你根据不完整的表格,解答下列问题:
成绩 x 分 频 数 频 率
50≤x<60 10
60≤ x <70 16 0.08
70≤ x <80 0.2
80≤ x <90 62 0.31
90≤ x <100 72 0.36
(1)补全频数分布表;
(2)随机抽取的样本容量为 ;
(3)若将得分转化为等级,规定50≤x<60评为“D”,60≤x<70评为“C”,70≤x<90评为“B”,90≤x<100评为“A”.估计这3000名学生中,有多少学生得分等级为A?
23.一个不透明的口袋装有若干个红、黄、蓝、绿四种颜色的小球,小球除颜色外完全相同,为估计该口袋中四种颜色的小球数量,每次从口袋中随机摸出一球记下颜色并放回,重复多次试验,汇总实验结果绘制如图不完整的条形统计图和扇形统计图.
根据以上信息解答下列问题:
(1)求实验总次数,并补全条形统计图;
(2)扇形统计图中,摸到黄色小球次数所在扇形的圆心角度数为多少度?
(3)已知该口袋中有10个红球,请你根据实验结果估计口袋中绿球的数量.
24.为了丰富校园文化生活,某校计划在午间校园广播台播放“百家讲坛”的部分内容.为了了解学生的喜好,抽取若干名学生进行问卷调查(每人只选一项内容),整理调查结果,绘制统计图如下:
请根据统计图提供的信息回答以下问题:
(1)抽取的学生数为____名;
(2)该校有3000名学生,估计喜欢收听易中天《品三国》的学生有____名;
(3)估计该校女学生喜欢收听刘心武评《红楼梦》的约占全校学生的____%;
(4)你认为上述估计合理吗?理由是什么?
25.利群商厦对销量较大的A、B、C三种品牌的纯牛奶进行了问卷调查,共发放问卷300份(问卷由单选和多选题组成),对收回的265份问卷进行了整理,部分数据如下:
(1)最近一次购买各品牌纯牛奶用户比例如图:
(2)用户对各品牌纯牛奶满意情况汇总如下表:
结合上述信息回答下列问题:
①A品牌牛奶的主要竞争优势是什么?请简要说明理由.
②广告对用户选择品牌有影响吗?请简要说明理由.
③你对厂家C有何建议?
26.为了了解我市中学生跳绳活动开展的情况,随机抽查了全市八年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制成如下的两个不完整的统计图:
请根据图中提供的信息,解答下列问题:
(1)本次共抽查了多少名学生?
(2)请补全频数分布直方图;
(3)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生的成绩为优秀;
(4)请你根据以上信息,对我市开展的学生跳绳活动情况谈谈自己的看法或建议.
参考答案
1.C
【解析】根据统计图的特点可知:
A. 本班学生的年龄统计,用条形统计图统计较合适;
B. 本班学生一年来的身高变化统计用折线统计图较合适;
C. 本班学生同时参加各种活动小组的比例统计,用扇形统计图较合适;
D. 本班学生穿鞋型号的统计,用条形统计图较合适;
故选:C.
点睛:此题考查了统计图的选择,条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.
2.B
【解析】试题解析根据题意得:360× EMBED Equation.DSMT4 =252(人),
答:该校八年级支持“分组合作学习”方式的学生约为252人;
故选B.
3.D
【解析】
试题分析:根据题意知了解报考军事院校考生的视力需要全面调查,故A错误;旅客上飞机前的安检需进行全面调查,故B错误;对招聘教师中的应聘人员进行面试需要全面调查,故C错误;了解全市中小学生每天的零花钱则适合抽样调查,故D正确.
故选D
考点:全面调查与抽样调查
4.C
【解析】
试题分析:根据统计图,喜欢足球所占的百比列=1-25%-15%-20%=40%,初三(1)班有同学50人,所以喜欢足球的人数==20
考点:统计
点评:本题考查统计,要求考生能识别统计图,能从统计图中得出对解答本题有用的信息来,本题难度不大
5.B
【解析】由题意可知,环境保护占“百姓热线”共接到热线电话总数的35%,
所以接到电话总数为:70÷35%=200个,
故选:B.
6.B
【解析】试题分析:先求出在随机调查的280名学生中希望举办文艺演出的学生所占的百分比,再用全校的人数乘以这个百分比数即可得到答案.
解:由题意知从全校1400名学生中随机调查了280名学生,其中有80人希望举办文艺演出,
∴希望举办文艺演出的学生所占的百分比为:80÷280=,
∴该学校希望举办文艺演出的学生人数为:1400×=400人.
故选B.
点评:本题考查了用样本估计总体的知识,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.
7.C
【解析】试题解析:调查的总人数:30÷ EMBED Equation.DSMT4 =90,
知道母亲的生日的学生数;90-10-30=50,
这所学校所有知道母亲的生日的学生:990×=550,
故选C.
考点:1.用样本估计总体;2.扇形统计图;3.条形统计图.
8.D
【解析】
试题分析:(15+20)÷(5+10+15+20)=0.7,
故选:D.
考点:频数(率)分布直方图
9.A.
【解析】
试题分析:读图可知:各小长方形的高之比AE:BF:CG:DH=2:4:3:1,即各组频数之比2:4:3:1,
则第2组的频数为×30=12,
故选A.
考点:频数(率)分布直方图.
10.B
【解析】试题分析:正确读取频数分布直方图的信息即可得出答案.
如图所示各阶段身高的人数分别为:[140.5,150.5]5人,[150.5,160.5]15人,[160.5,170.5]20人,[170.5,180.5]7人.所以,该班人数最多的身高段的学生数应为20人,A选项错误;该班身高最高段的学生数为7人,B选项正确C选项错误;该班身高低于160.5cm的学生数为:5+15="20" (人),D选项错误.
考点:直方图.
11.C
【解析】试题解析:A、条形统计图能清楚地表示出每个项目的数据,故此选项错误;
B、折线统计图能清楚地反映事物的变化情况,故此选项错误;
C、扇形统计图直接反映部分占总体的百分比大小,故此选项正确;
D、这三种统计图可以互相转化,但是各有利弊,不是经常互相转化,故此选项错误.
故选C.
点睛:本题考查的是条形统计图和扇形统计图、折线统计图的不同,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小,折线统计图能清楚地反映事物的变化情况.
12.D
【解析】试题解析:在图中,从5月1日至5月7日找出实线与虚线差距最大的一天,为5月5日;
故选D.
13.抽样调查
【解析】试题解析:为了尝味道,应采用的合适的调查方式为抽样调查,
故答案为:抽样调查.
14.0.2.
【解析】
试题分析:根据频率=即可求解.
试题解析:频率==0.2.
考点:频数与频率.
15.150
【解析】
试题分析:由图可知:售出红豆口味的雪糕200支,占40%,
∴售出雪糕总量为200÷40%=500支,
∵水果口味的占30%,
∴水果口味的有500×30%=150支,
故答案为150.考点:统计初步
16.286
【解析】试题解析:奖牌数量为:32+28+54+50+59+63=286(枚).
故答案为:286.
17.10000
【解析】由题意可知:重新捕获500只,其中带标记的有5只,可以知道,在样本中,有标记的占到.而在总体中,有标记的共有100只,根据比例即可解答.
解:100=10000只.
故答案为:10000.
18. 0.4 12
【解析】试题解析:读图可知:各小长方形的高之比AE:BF:CG:DH=2:4:3:1,即各组频数之比2:4:3:1,
则第2组的频数为×30=12,其频率为=0.4.
故本题答案为:0.4;12.
19.140吨
【解析】试题分析:水表显示了七天的数据,但实际上是调查了六天的用水情况.用这六天的用水平均值估计本月的即可.
试题解析:从表中可以看出这6天的平均用水量是吨,
4月份的用水量是=140吨.
20.统计表如下
鸟 名 喜鹊 丹顶鹤 绿孔雀 鸳鸯
营巢环境 大乔木 浅滩.深草丛 灌木丛.竹丛间 树洞
体长(cm) 41~52cm 约140cm 100~230 cm 38~44cm
产卵枚数 5~8 2 4~8 7~12
从统计表可以看出:(1)丹顶鹤和其他三种鸟相比,它的营巢环境要求比较高,而产卵数量比较少,这些可能是丹顶鹤被列为国家一级保护动物的部分原因;(2)鸟类的体长与产卵数量没有明显的关系,等等.
【解析】
试题分析:仔细分析题意即可得到统计表,再根据统计表中的信息即可发现结论.
统计表如下
鸟 名 喜鹊 丹顶鹤 绿孔雀 鸳鸯
营巢环境 大乔木 浅滩.深草丛 灌木丛.竹丛间 树洞
体长(cm) 41~52cm 约140cm 100~230 cm 38~44cm
产卵枚数 5~8 2 4~8 7~12
从统计表可以看出:(1)丹顶鹤和其他三种鸟相比,它的营巢环境要求比较高,而产卵数量比较少,这些可能是丹顶鹤被列为国家一级保护动物的部分原因;(2)鸟类的体长与产卵数量没有明显的关系,等等.
考点:统计表的制作,从统计表中获取信息的能力
点评:本题是统计表的基础应用题,难度一般,学生需认识到统计表可以将大量数据的分类结果清晰、一目了然地表达出来.
21.(1)文艺小组;(2)美术小组与科技小组;(3)答案不唯一;(4)不能
【解析】试题分析:(1)--(3)小问根据扇形统计图所给比例即可求解;
(4)不知学生总数,故无法求解.
试题解析:(1)文艺小组是最受欢迎的课外活动小组,因为它所占的百分比最高.
(2)美术小组与科技小组所占人数的百分比分别为28%和25%,所以这两个课外活动小组的受欢迎程度较为接近.
(3)答案不唯一,如:书法小组参加的人数较少,应该鼓励其他人参加,等.
(4)不能.不知参加课外活动的总人数,也不知任何一个小组的人数.
22.(1)40,0.05 (2)200 (3)1080名
【解析】
试题分析:(1)找出样本中评为“D”的百分比,估计出总体中“D”的人数即可;根据频率和总量的关系,求出70≤x<80分数段的频数;
(2)根据其中已知的频数和频率,可根据总频数=频数÷频率,求得样本容量;
(3)求出等级为A的频率可以求出等级为A的人数.
试题解析:解:(1)70≤x<80分数段的频数40(人),
50≤x<60分数段频率为0.05;
(2)200
(3)根据题意得:3000×0.36=1080,
所以这3000名学生中,有1080名学生得分等级为A.
考点:频率,频数,样本容量,概率
23.(1)200,作图见解析;(2)144°;(3)2.
【解析】试题分析:(1)用摸到红色球的次数除以占的百分比即是实验总次数,用总次数减去红黄绿球的次数即为摸蓝球的次数,再补全条形统计图即可;
(2)用摸到黄色小球次数除以实验总次数,再乘以360°即可得摸到黄色小球次数所在扇形的圆心角度数;
(3)先得出摸到绿色小球次数所占的百分比,再用口袋中有10个红球除以红球所占的百分比得出口袋中小球的总数,最后乘以绿色小球所占的百分比即可.
解:(1)50÷25%=200(次),
所以实验总次数为200次,
条形统计图如下:
(2)=144°;
(3)10÷25%×=2(个),
答:口袋中绿球有2个.
考点:条形统计图;扇形统计图;模拟实验.
24.1.300;2.1060;3.15.4.合理.
【解析】试题分析:(1)男女生所有人数之和;
(2)求出抽取的样本中收听品三国的学生所占的比例,乘3000即可求解;
(3)听红楼梦的女生人数除以总人数.
试题解析:(1)20+10+30+15+30+38+64+42+6+45=300人;
(2) EMBED Equation.DSMT4 ×3000=1060人;
(3)样本中校女学生喜欢收听刘心武评《红楼梦》的约占样本容量的百分比为45÷300=15%,
则该校女学生喜欢收听刘心武评《红楼梦》的约占全校学生的15%;
(4)合理.理由中体现用样本估计总体即可.
考点:1.条形统计图;2.用样本估计总体.
25.(1)理由见解析;(2)理由见解析;(3)建议见解析.
【解析】试题分析:(1)结合统计图表,从购买量、质量、广告、价格等方面进行分析即可;
(2)结合图表中反映的例子进行分析即可;
(3)从厂家C的劣势进行建议即可.
试题解析:(1)A品牌牛奶的主要竞争优势是质量好,因为对此品牌牛奶的质量满意的用户最多,而对其广告、价格满意的用户不是最多。
(2)广告对用户选择品牌有影响,因为对于B、C两种品牌的纯牛奶在质量和价格上顾客满意率是相同的,但由于B品牌牛奶广告做得好,所以销量比C品牌大。
(3)厂家C在提高质量和降低价格的同时,加大宣传力度,重视广告效用。
26.(1) 200名;(2) 图形见解析;(3) 4200名;(4)见解析.
【解析】试题分析:(1)利用95≤x<115的人数是8+16=24人,所占的比例是12%即可求解;
(2)求得范围是115≤x<145的人数,扇形的圆心角度数是360度乘以对应的比例即可求解;
(3)首先求得所占的比例,然后乘以总人数8000即可求解;
(4)根据实际情况,提出自己的见解即可,答案不唯一.
试题解析:(1)(16+8)÷12%=200(名)
(2)范围是135≤x<145的人数是:200-8-16-71-60-16=29(人),
则跳绳次数范围135≤x<155所在扇形的圆心角度数是:360×=81°.
;
(3)优秀的比例是:×100%=52.5%,
则估计全市8000名八年级学生中有多少名学生的成绩为优秀人数是:8000×52.5%=4200(人);
(4)全市达到优秀的人数有一半以上,反映了我市学生锻炼情况很好.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
