20.1.2 中位数和众数同步练习
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
20.1.2 中位数和众数同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.将一组数据按照由小到大(或由大到小) ( http: / / www.21cnjy.com )的顺序排列,如果数据的个数是奇数,则处于中间位置的数,称为这组数据的中位数;如果数据的个数是偶数,则处于中间两个数据的平均数,称为这组数据的中位数. 21教育名师原创作品
2.中位数是一个位置代表值,利用中位数分析数据可以获得一些信息.当一组数据中的个别数据相差较大时,可用中位数来描述这组数据的集中趋势.
4一组数据中 出现次数(频数)最多的数据,称为这组数据的众数.
5.如果一组数据中有两个数据的频数一样,都是最大,那么这两个数据都是这组数据的众数.
6.众数考察的是各数据出现的次数,当一组数据有某些数据多次重复出现时,众数往往更能反映数据的平均水平.
基础知识和能力拓展精练
一、选择题
1.2,3,14,16,7,8,10,11,13的中位数是( )
A. 3 B. 7 C. 10 D. 13
2.下列数据85,88,73,88,79,85的众数是( )
A. 88 B. 73 C. 88,85 D. 85
3.在描述一组数据的集中趋势时,应用最广泛的是( )
A. 众数 B. 中位数 C. 平均数 D. 全体数据
4.某居民小区开展节约用电活动,对该小区30户家庭的节电量情况进行了统计,五月份与四月份相比,节电情况如下表:
节电量(度) 10 20 30 40
户数 2 15 10 3
则五月份这30户家庭节电量的众数与中位数分别为( )
A. 20,20 B. 20,25 C. 30,25 D. 40,20
5.在下面各组数据中,众数是3.5的是( )
A. 4,3,4,3 B. 1.5,2,2.5,3.5
C. 3.5,4.5,3.5 D. 6,4,3,2
6.甲、乙、丙、丁四人的数学测验成绩分别为 ( http: / / www.21cnjy.com )90分、90分、x分、80分,若这组数据的众数与平均数恰好相等,则这组数据的中位数是( )21*cnjy*com
A. 100分 B. 95分 C. 90分 D. 85分
7.7.一组数据按从小到大的顺序排列为:1,2,3,x,6,9,这组数据的中位数是4.5,那么这组数据的众数为( )
A. 4 B. 5 C. 5.5 D. 6
8.小芸所在学习小组的同学们,响应“为祖国 ( http: / / www.21cnjy.com )争光,为奥运添彩”的号召,主动到附近的7个社区帮助爷爷、奶奶们学习英语日常用语.他们记录的各社区参加其中一次活动的人数如下:33,32,32,31,28,26,32,那么这组数据的众数和中位数分别是( )
A. 32,31 B. 32,32 C. 3,31 D. 3,32
二、填空题
9.3,5,8,9,7,6,2的中位数是_____.
10.十名工人某天生产同一 ( http: / / www.21cnjy.com )种零件,生产的件数分别是:15,17,14,10,15,19,17,16,14,12,则这一天10名工人生产零件件数的中位数是____件.
11.下表是某校随机抽查的20名八年级男生的身高统计表:
身高(cm) 150 155 160 163 165 168
人数(人) 1 3 4 4 5 3
这组数据的众数是__cm,中位数是__cm.
12.数学老师布置了10道选择题,小颖 ( http: / / www.21cnjy.com )将全班同学的解答情况绘成了下面的条形统计图,根据图表回答:平均每个学生做对了_____道题,做对题目的众数是_____,中位数是_____.
( http: / / www.21cnjy.com )
13.从甲、乙、丙三个厂家生产的同一种产品中,各抽出8种产品,对其使用寿命进行跟踪调查,结果如下(单位:年):【来源:21·世纪·教育·网】
甲:3,4,5,6,8,8,8,10
乙:4,6,6,6,8,9,12,13
丙:3,3,4,7,9,10,11,12
三个厂家在广告中都称该产品使用寿命为8年,根据调查结果判断厂家在广告中分别运用了平均数、众数、中位数中哪一个集中趋势的特征数www-2-1-cnjy-com
甲:____,乙:__________,丙:________.
14.某市近8日每日最高气温折线统计图如图所示,这组每日最高气温数据的位数是_____度.
( http: / / www.21cnjy.com )
三、解答题
15.某学校积极响应上级的号召,举行了“决不让一个学生因贫困而失学”的捐资助学活动,其中6个班同学的捐款平均数如下表:【来源:21cnj*y.co*m】
班级 一班 二班 三班 四班 五班 六班
捐款平均数(元) 6 4.6 4.1 3.8 4.8 5.2
则这组数据的中位数是多少元?
16.乐乐是一名健步走运动的爱好者 ( http: / / www.21cnjy.com ),她用手机软件记录了某个月(30 天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).
(1)若乐乐这个月平均每天健步走的步数为 1.32 万步,试求她走 1.3 万步和 1.5 万步的天数;21世纪教育网版权所有
(2)求这组数据中的众数和中位数.
( http: / / www.21cnjy.com )
17.在“爱满金陵”慈善一日捐活动中,学校团总支为了了解本校写生的捐款情况,随机抽取了名学生的捐款数进行了统计,并绘制成统计图.21·世纪*教育网
( http: / / www.21cnjy.com )
()这名同学捐款的众数为__________元,中位数为__________.
()求这名同学捐款的平均数.
()该校共有名学生参与捐款,请估计该校学生的捐款总数.
18.下表是某校八年级(1)班43名学生右眼视力的检查结果.
( http: / / www.21cnjy.com )(1)该班学生右眼视力的平均数是________(结果保留1位小数).
(2)该班学生右眼视力的中位数是________.
(3)该班小鸣同学右眼视力是4.5,能不能说小鸣同学的右眼视力处于全班同学的中上水平?试说明理由.
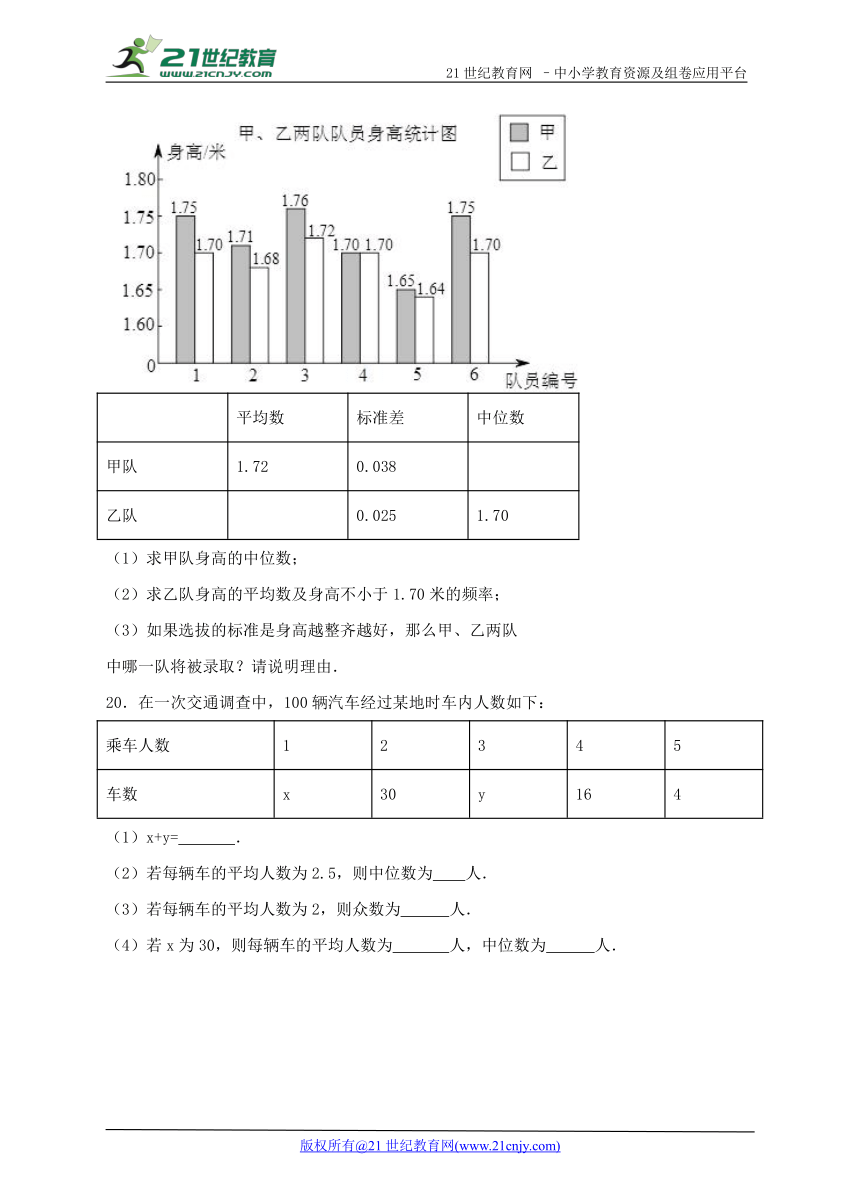
19.某学校要成立一支由6名女生组 ( http: / / www.21cnjy.com )成的礼仪队,八年级两个班各选6名女生,分别组成甲队和乙队参加选拔.每位女生的身高统计如图,部分统计量如下表:【版权所有:21教育】
( http: / / www.21cnjy.com )
平均数 标准差 中位数
甲队 1.72 0.038
乙队 0.025 1.70
(1)求甲队身高的中位数;
(2)求乙队身高的平均数及身高不小于1.70米的频率;
(3)如果选拔的标准是身高越整齐越好,那么甲、乙两队
中哪一队将被录取?请说明理由.
20.在一次交通调查中,100辆汽车经过某地时车内人数如下:
乘车人数 1 2 3 4 5
车数 x 30 y 16 4
(1)x+y= .
(2)若每辆车的平均人数为2.5,则中位数为 人.
(3)若每辆车的平均人数为2,则众数为 人.
(4)若x为30,则每辆车的平均人数为 人,中位数为 人.
参考答案
1.C
【解析】解:把数据2,3,14,16,7,8,10,11,13按从小到大排列,得到第5个数为10.所以中位数是10.故选C.21·cn·jy·com
2.C
【解析】解:数据85,88,73,88,79,85有两个众数,它们是88,85.故选C.
3.C
【解析】解:由于平均数反映的是这级数据的平均大小,使用最广泛.故选C.
4.A
【解析】试题解析:由表格中的数据可得,
五月份这30户家庭节电量的众数是:20,中位数是20,
故选A.
5.C
【解析】解:四个选项中只有C中3.5出现的次数最多(2次).故选C.
6.C
【解析】①众数是90时,∵众数与平均数相等,∴(90+90+x+80)=90,解得x=100.这组数据为:80,90,90,100,∴中位数为90.②当众数是80时,∵众数与平均数相等,∴(90+90+x+80)=80,解得x=60,故不可能.所以这组数据中的中位数是90.故选C.
点睛:本题众数可能是90,也可能是80,因此应分众数是90或者众数是80两种情况进行讨论.正确运用分类讨论的思想是解答本题的关键. www.21-cn-jy.com
7.D
【解析】解:据题意得,处于这组数据中间位置的那两个数是3、x.
那么由中位数的定义可知,这组数据的中位数是,
所以,故众数是6.
故选D.
8.B
【解析】解:在这一组数据中32是出现次数最多的,故众数是32;
而将这组数据从小到大的顺序排列后,处于中间位置的那个数是32,那么由中位数的定义可知,这组数据的中位数是32.故选B.2-1-c-n-j-y
点睛:本题考查了统计的有关知识,找中位数要把 ( http: / / www.21cnjy.com )数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不只一个.【出处:21教育名师】
9.6
【解析】解:将这组数据从小到大重新排列后为2,3,5,6,7,8,9.最中间的那个数是6,所以中位数是6.故答案为:6.21*cnjy*com
10.15
【解析】解:题目中数据共有10个,
故中位数是按从小到大排列后第5,第6个数的平均数作为中位数,
故这组数据的中位数是.
故答案为:15.
11. 165 163
【解析】解:众数是一组数据中出现次数最多的数,在这一组数据中165是出现次数最多的,故众数是165;
而将这组数据从小到大的顺序排列后,处于中间位置的2个数的平均数是163,那么由中位数的定义可知,这组数据的中位数是163.
故答案为:165,163.
12. 8.625 9 9
【解析】解:平均数;
由图可直接得出众数是9(道);中位数是9(道).
故答案为:8.625;9;9.
13. 众数 平均数 中位数
【解析】解:对甲分析:8出现的次数最多,故运用了众数;
对乙分析:8既不是众数,也不是中位数,求数据的平均数可得,平均数=(4+6+6+6+8+9+12+13)÷8=8,故运用了平均数;
对丙分析:共8个数据,最中间的是7与9,故其中位数是8,即运用了中位数.
故答案为:众数;平均数;中位数.
14.11
【解析】根据中位数的意义,先把这组数据重新排列为6、8、10、10、12、14、14、16,则这组数据的中位数为=11,
故答案为:11.
点睛:此题主要考查了中位数 ( http: / / www.21cnjy.com ),关键是把数据按从大到小或从小到大排列,然后取中间的一个(数据的个数为奇数)或中间两个(数据的个数为偶数个)的平均数即可得到中位数.
15.中位数是4.7
【解析】试题分析:找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数.
试题解析:解:由中位数的 ( http: / / www.21cnjy.com )定义可知,这组数据从大到小排列为:3.8,4.1,4.6,4.8,5.2,6,∴其中位数是(4.6+4.8)÷2=4.7.
点睛:本题为统计题,考查中位数的意义. ( http: / / www.21cnjy.com )中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数.
16.(1)6天,4天;(2)众数是1.4万步,中位数为1.3万步
【解析】(1)设乐乐有天每天走1.3万步,有天每天走1.5万步,
则
解得
即乐乐有6天每天走1.3万步,有4天每天走1.5万步.
(2)众数是1.4万步,中位数为1.3万步.
17.(1)15,15;(2)13;(3)7800元.
【解析】试题分析:(1)根据众数的定义即出现次数最多的数据进而得出即可,再利用中位数的定义得出即可;21教育网
(2)利用条形统计图得出各组频数,再根据加权平均数的公式计算即可;
(3)利用样本估计总体的思想,用总数乘以捐款平均数即可得到捐款总数.
试题解析:解:(1)数据15元出现了20次,出现次数最多,所以众数是15元;
数据总数为50,所以中位数是第25、26位数的平均数,即(15+15)÷2=15(元).
故答案为:15,15;
(2)50名同学捐款的平均数=(5×8+10×14+15×20+20×6+25×2)÷50=13(元);
(3)估计这个中学的捐款总数=600×13=7800(元).
点睛:本题考查的是条形统计图的综合运用 ( http: / / www.21cnjy.com ).读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.除此之外,本题也考查了平均数、中位数、众数的定义以及利用样本估计总体的思想.2·1·c·n·j·y
18.(1)4.6;(2)4.7;(3)不能.
【解析】试题分析:(1)根据加权平均数公式求解即可;
(2)首先将这组数据按照从小到大的顺序排列,中位数为第22个数据;
(3)根据小鸣同学右眼视力是4.5,小于中位数4.7,故此可得到问题的答案.
试题解析:(1)该班学生右眼视力的平均数是
×(4.0+4.1×2+4.2×5+4.3×4+4.4×3+4.5×5+4.6+4.7+4.8×5+4.9×10+5.0×6)≈4.6,
故答案为:4.6;
(2)由于共有43个数据,其中位数为第22个数据,即中位数为4.7,
故答案为:4.7;
(3)不能,
∵小鸣同学右眼视力是4.5,小于中位数4.7,
∴不能说小鸣同学的右眼视力处于全班同学的中上水平.
【点睛】本题考查了平均数、中位数的 ( http: / / www.21cnjy.com )意义,掌握平均数的计算公式,找中位数的方法是解题的关键.找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数.如果数据有奇数个,则正中间的数字即为所求;如果是偶数个,则找中间两位数的平均数.
19.(1)1.73米;(2)1.69, (3)乙队,理由:标准差小,数据波动小
【解析】试题分析:(1)根据中位数的定义,把甲队队员身高从高到矮排列,找出位置处于中间的数即可;
(2)根据条形图可得到乙队队员每个人的身 ( http: / / www.21cnjy.com )高,再用总身高÷队员人数=平均数身高;身高不小于1.70米的频率=身高不小于1.70米的人数÷乙队队员总数;
(3)根据标准差的意义可以得到答案;标准差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
试题解析:(1)把甲队队员身高从高到矮排列:1.76,1.75,1.75,1.71,1.70,1.65,
位置处于中间的两数为:1.75,1.71,
故甲队身高的中位数是=1.73米;
(2)x乙=×(1.70+1.68+1.72+1.70+1.64+1.70)=1.69米,
故乙队身高的平均数是1.69米,
身高不低于1.70米的频率为 ;
(3)∵S乙<S甲,
∴乙队的身高比较整齐,乙队将被录取.
20.(1)50(2)2;(3)1;(4)2.34;2.
【解析】试题分析:车数的和为100,可得到x+y的值;通过平均数求出x和y,然后根据中位数、众数的定义求解.21cnjy.com
试题解析:解:(1)由题意得x+30+y+16+4=100,所以x+y=50.
(2) ,
解得.
所以第50个,51个数据均为2,即中位数为2(人).
(3),
解得.
所以众数为1(人).
(4)x=30时,y=20.
因此(人)
第50个,51个数据都是2,所以中位数为(人).
点睛:本题为统计题,考查平均数、众数与中位数的意义.解题的关键是准确理解题意,建立等量关系.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
20.1.2 中位数和众数同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.将一组数据按照由小到大(或由大到小) ( http: / / www.21cnjy.com )的顺序排列,如果数据的个数是奇数,则处于中间位置的数,称为这组数据的中位数;如果数据的个数是偶数,则处于中间两个数据的平均数,称为这组数据的中位数. 21教育名师原创作品
2.中位数是一个位置代表值,利用中位数分析数据可以获得一些信息.当一组数据中的个别数据相差较大时,可用中位数来描述这组数据的集中趋势.
4一组数据中 出现次数(频数)最多的数据,称为这组数据的众数.
5.如果一组数据中有两个数据的频数一样,都是最大,那么这两个数据都是这组数据的众数.
6.众数考察的是各数据出现的次数,当一组数据有某些数据多次重复出现时,众数往往更能反映数据的平均水平.
基础知识和能力拓展精练
一、选择题
1.2,3,14,16,7,8,10,11,13的中位数是( )
A. 3 B. 7 C. 10 D. 13
2.下列数据85,88,73,88,79,85的众数是( )
A. 88 B. 73 C. 88,85 D. 85
3.在描述一组数据的集中趋势时,应用最广泛的是( )
A. 众数 B. 中位数 C. 平均数 D. 全体数据
4.某居民小区开展节约用电活动,对该小区30户家庭的节电量情况进行了统计,五月份与四月份相比,节电情况如下表:
节电量(度) 10 20 30 40
户数 2 15 10 3
则五月份这30户家庭节电量的众数与中位数分别为( )
A. 20,20 B. 20,25 C. 30,25 D. 40,20
5.在下面各组数据中,众数是3.5的是( )
A. 4,3,4,3 B. 1.5,2,2.5,3.5
C. 3.5,4.5,3.5 D. 6,4,3,2
6.甲、乙、丙、丁四人的数学测验成绩分别为 ( http: / / www.21cnjy.com )90分、90分、x分、80分,若这组数据的众数与平均数恰好相等,则这组数据的中位数是( )21*cnjy*com
A. 100分 B. 95分 C. 90分 D. 85分
7.7.一组数据按从小到大的顺序排列为:1,2,3,x,6,9,这组数据的中位数是4.5,那么这组数据的众数为( )
A. 4 B. 5 C. 5.5 D. 6
8.小芸所在学习小组的同学们,响应“为祖国 ( http: / / www.21cnjy.com )争光,为奥运添彩”的号召,主动到附近的7个社区帮助爷爷、奶奶们学习英语日常用语.他们记录的各社区参加其中一次活动的人数如下:33,32,32,31,28,26,32,那么这组数据的众数和中位数分别是( )
A. 32,31 B. 32,32 C. 3,31 D. 3,32
二、填空题
9.3,5,8,9,7,6,2的中位数是_____.
10.十名工人某天生产同一 ( http: / / www.21cnjy.com )种零件,生产的件数分别是:15,17,14,10,15,19,17,16,14,12,则这一天10名工人生产零件件数的中位数是____件.
11.下表是某校随机抽查的20名八年级男生的身高统计表:
身高(cm) 150 155 160 163 165 168
人数(人) 1 3 4 4 5 3
这组数据的众数是__cm,中位数是__cm.
12.数学老师布置了10道选择题,小颖 ( http: / / www.21cnjy.com )将全班同学的解答情况绘成了下面的条形统计图,根据图表回答:平均每个学生做对了_____道题,做对题目的众数是_____,中位数是_____.
( http: / / www.21cnjy.com )
13.从甲、乙、丙三个厂家生产的同一种产品中,各抽出8种产品,对其使用寿命进行跟踪调查,结果如下(单位:年):【来源:21·世纪·教育·网】
甲:3,4,5,6,8,8,8,10
乙:4,6,6,6,8,9,12,13
丙:3,3,4,7,9,10,11,12
三个厂家在广告中都称该产品使用寿命为8年,根据调查结果判断厂家在广告中分别运用了平均数、众数、中位数中哪一个集中趋势的特征数www-2-1-cnjy-com
甲:____,乙:__________,丙:________.
14.某市近8日每日最高气温折线统计图如图所示,这组每日最高气温数据的位数是_____度.
( http: / / www.21cnjy.com )
三、解答题
15.某学校积极响应上级的号召,举行了“决不让一个学生因贫困而失学”的捐资助学活动,其中6个班同学的捐款平均数如下表:【来源:21cnj*y.co*m】
班级 一班 二班 三班 四班 五班 六班
捐款平均数(元) 6 4.6 4.1 3.8 4.8 5.2
则这组数据的中位数是多少元?
16.乐乐是一名健步走运动的爱好者 ( http: / / www.21cnjy.com ),她用手机软件记录了某个月(30 天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).
(1)若乐乐这个月平均每天健步走的步数为 1.32 万步,试求她走 1.3 万步和 1.5 万步的天数;21世纪教育网版权所有
(2)求这组数据中的众数和中位数.
( http: / / www.21cnjy.com )
17.在“爱满金陵”慈善一日捐活动中,学校团总支为了了解本校写生的捐款情况,随机抽取了名学生的捐款数进行了统计,并绘制成统计图.21·世纪*教育网
( http: / / www.21cnjy.com )
()这名同学捐款的众数为__________元,中位数为__________.
()求这名同学捐款的平均数.
()该校共有名学生参与捐款,请估计该校学生的捐款总数.
18.下表是某校八年级(1)班43名学生右眼视力的检查结果.
( http: / / www.21cnjy.com )(1)该班学生右眼视力的平均数是________(结果保留1位小数).
(2)该班学生右眼视力的中位数是________.
(3)该班小鸣同学右眼视力是4.5,能不能说小鸣同学的右眼视力处于全班同学的中上水平?试说明理由.
19.某学校要成立一支由6名女生组 ( http: / / www.21cnjy.com )成的礼仪队,八年级两个班各选6名女生,分别组成甲队和乙队参加选拔.每位女生的身高统计如图,部分统计量如下表:【版权所有:21教育】
( http: / / www.21cnjy.com )
平均数 标准差 中位数
甲队 1.72 0.038
乙队 0.025 1.70
(1)求甲队身高的中位数;
(2)求乙队身高的平均数及身高不小于1.70米的频率;
(3)如果选拔的标准是身高越整齐越好,那么甲、乙两队
中哪一队将被录取?请说明理由.
20.在一次交通调查中,100辆汽车经过某地时车内人数如下:
乘车人数 1 2 3 4 5
车数 x 30 y 16 4
(1)x+y= .
(2)若每辆车的平均人数为2.5,则中位数为 人.
(3)若每辆车的平均人数为2,则众数为 人.
(4)若x为30,则每辆车的平均人数为 人,中位数为 人.
参考答案
1.C
【解析】解:把数据2,3,14,16,7,8,10,11,13按从小到大排列,得到第5个数为10.所以中位数是10.故选C.21·cn·jy·com
2.C
【解析】解:数据85,88,73,88,79,85有两个众数,它们是88,85.故选C.
3.C
【解析】解:由于平均数反映的是这级数据的平均大小,使用最广泛.故选C.
4.A
【解析】试题解析:由表格中的数据可得,
五月份这30户家庭节电量的众数是:20,中位数是20,
故选A.
5.C
【解析】解:四个选项中只有C中3.5出现的次数最多(2次).故选C.
6.C
【解析】①众数是90时,∵众数与平均数相等,∴(90+90+x+80)=90,解得x=100.这组数据为:80,90,90,100,∴中位数为90.②当众数是80时,∵众数与平均数相等,∴(90+90+x+80)=80,解得x=60,故不可能.所以这组数据中的中位数是90.故选C.
点睛:本题众数可能是90,也可能是80,因此应分众数是90或者众数是80两种情况进行讨论.正确运用分类讨论的思想是解答本题的关键. www.21-cn-jy.com
7.D
【解析】解:据题意得,处于这组数据中间位置的那两个数是3、x.
那么由中位数的定义可知,这组数据的中位数是,
所以,故众数是6.
故选D.
8.B
【解析】解:在这一组数据中32是出现次数最多的,故众数是32;
而将这组数据从小到大的顺序排列后,处于中间位置的那个数是32,那么由中位数的定义可知,这组数据的中位数是32.故选B.2-1-c-n-j-y
点睛:本题考查了统计的有关知识,找中位数要把 ( http: / / www.21cnjy.com )数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不只一个.【出处:21教育名师】
9.6
【解析】解:将这组数据从小到大重新排列后为2,3,5,6,7,8,9.最中间的那个数是6,所以中位数是6.故答案为:6.21*cnjy*com
10.15
【解析】解:题目中数据共有10个,
故中位数是按从小到大排列后第5,第6个数的平均数作为中位数,
故这组数据的中位数是.
故答案为:15.
11. 165 163
【解析】解:众数是一组数据中出现次数最多的数,在这一组数据中165是出现次数最多的,故众数是165;
而将这组数据从小到大的顺序排列后,处于中间位置的2个数的平均数是163,那么由中位数的定义可知,这组数据的中位数是163.
故答案为:165,163.
12. 8.625 9 9
【解析】解:平均数;
由图可直接得出众数是9(道);中位数是9(道).
故答案为:8.625;9;9.
13. 众数 平均数 中位数
【解析】解:对甲分析:8出现的次数最多,故运用了众数;
对乙分析:8既不是众数,也不是中位数,求数据的平均数可得,平均数=(4+6+6+6+8+9+12+13)÷8=8,故运用了平均数;
对丙分析:共8个数据,最中间的是7与9,故其中位数是8,即运用了中位数.
故答案为:众数;平均数;中位数.
14.11
【解析】根据中位数的意义,先把这组数据重新排列为6、8、10、10、12、14、14、16,则这组数据的中位数为=11,
故答案为:11.
点睛:此题主要考查了中位数 ( http: / / www.21cnjy.com ),关键是把数据按从大到小或从小到大排列,然后取中间的一个(数据的个数为奇数)或中间两个(数据的个数为偶数个)的平均数即可得到中位数.
15.中位数是4.7
【解析】试题分析:找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数.
试题解析:解:由中位数的 ( http: / / www.21cnjy.com )定义可知,这组数据从大到小排列为:3.8,4.1,4.6,4.8,5.2,6,∴其中位数是(4.6+4.8)÷2=4.7.
点睛:本题为统计题,考查中位数的意义. ( http: / / www.21cnjy.com )中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数.
16.(1)6天,4天;(2)众数是1.4万步,中位数为1.3万步
【解析】(1)设乐乐有天每天走1.3万步,有天每天走1.5万步,
则
解得
即乐乐有6天每天走1.3万步,有4天每天走1.5万步.
(2)众数是1.4万步,中位数为1.3万步.
17.(1)15,15;(2)13;(3)7800元.
【解析】试题分析:(1)根据众数的定义即出现次数最多的数据进而得出即可,再利用中位数的定义得出即可;21教育网
(2)利用条形统计图得出各组频数,再根据加权平均数的公式计算即可;
(3)利用样本估计总体的思想,用总数乘以捐款平均数即可得到捐款总数.
试题解析:解:(1)数据15元出现了20次,出现次数最多,所以众数是15元;
数据总数为50,所以中位数是第25、26位数的平均数,即(15+15)÷2=15(元).
故答案为:15,15;
(2)50名同学捐款的平均数=(5×8+10×14+15×20+20×6+25×2)÷50=13(元);
(3)估计这个中学的捐款总数=600×13=7800(元).
点睛:本题考查的是条形统计图的综合运用 ( http: / / www.21cnjy.com ).读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.除此之外,本题也考查了平均数、中位数、众数的定义以及利用样本估计总体的思想.2·1·c·n·j·y
18.(1)4.6;(2)4.7;(3)不能.
【解析】试题分析:(1)根据加权平均数公式求解即可;
(2)首先将这组数据按照从小到大的顺序排列,中位数为第22个数据;
(3)根据小鸣同学右眼视力是4.5,小于中位数4.7,故此可得到问题的答案.
试题解析:(1)该班学生右眼视力的平均数是
×(4.0+4.1×2+4.2×5+4.3×4+4.4×3+4.5×5+4.6+4.7+4.8×5+4.9×10+5.0×6)≈4.6,
故答案为:4.6;
(2)由于共有43个数据,其中位数为第22个数据,即中位数为4.7,
故答案为:4.7;
(3)不能,
∵小鸣同学右眼视力是4.5,小于中位数4.7,
∴不能说小鸣同学的右眼视力处于全班同学的中上水平.
【点睛】本题考查了平均数、中位数的 ( http: / / www.21cnjy.com )意义,掌握平均数的计算公式,找中位数的方法是解题的关键.找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数.如果数据有奇数个,则正中间的数字即为所求;如果是偶数个,则找中间两位数的平均数.
19.(1)1.73米;(2)1.69, (3)乙队,理由:标准差小,数据波动小
【解析】试题分析:(1)根据中位数的定义,把甲队队员身高从高到矮排列,找出位置处于中间的数即可;
(2)根据条形图可得到乙队队员每个人的身 ( http: / / www.21cnjy.com )高,再用总身高÷队员人数=平均数身高;身高不小于1.70米的频率=身高不小于1.70米的人数÷乙队队员总数;
(3)根据标准差的意义可以得到答案;标准差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
试题解析:(1)把甲队队员身高从高到矮排列:1.76,1.75,1.75,1.71,1.70,1.65,
位置处于中间的两数为:1.75,1.71,
故甲队身高的中位数是=1.73米;
(2)x乙=×(1.70+1.68+1.72+1.70+1.64+1.70)=1.69米,
故乙队身高的平均数是1.69米,
身高不低于1.70米的频率为 ;
(3)∵S乙<S甲,
∴乙队的身高比较整齐,乙队将被录取.
20.(1)50(2)2;(3)1;(4)2.34;2.
【解析】试题分析:车数的和为100,可得到x+y的值;通过平均数求出x和y,然后根据中位数、众数的定义求解.21cnjy.com
试题解析:解:(1)由题意得x+30+y+16+4=100,所以x+y=50.
(2) ,
解得.
所以第50个,51个数据均为2,即中位数为2(人).
(3),
解得.
所以众数为1(人).
(4)x=30时,y=20.
因此(人)
第50个,51个数据都是2,所以中位数为(人).
点睛:本题为统计题,考查平均数、众数与中位数的意义.解题的关键是准确理解题意,建立等量关系.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
