2018年高考数学百强校大题狂练系列(通用版)专题3.5+频率分布直方图与数字特征
文档属性
| 名称 | 2018年高考数学百强校大题狂练系列(通用版)专题3.5+频率分布直方图与数字特征 |  | |
| 格式 | zip | ||
| 文件大小 | 740.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-25 15:10:43 | ||
图片预览



文档简介
2018届高考数学大题狂练
第三篇 概率与统计专题05 频率分布直方图与数字特征
1.为选拔选手参加“中国诗词大会”,某中学举行一次“诗词大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为)进行统计.按照, , , , 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在, 的数据).
(1)求样本容量和频率分布直方图中、的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“中国谜语大会”,设随机变量表示所抽取的2名学生中得分在内的学生人数,求随机变量的分布列及数学期望.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)由频率分布直方图及题意可得样本容量与、的值;(2)抽取的2名学生中得分在的人数X可能取值0,1,2,求出相应的概率值,即可得到随机变量的分布列及数学期望.
抽取的2名学生中得分在的人数X可能取值0,1,2,
则, , ,
则的分布列为
所以.
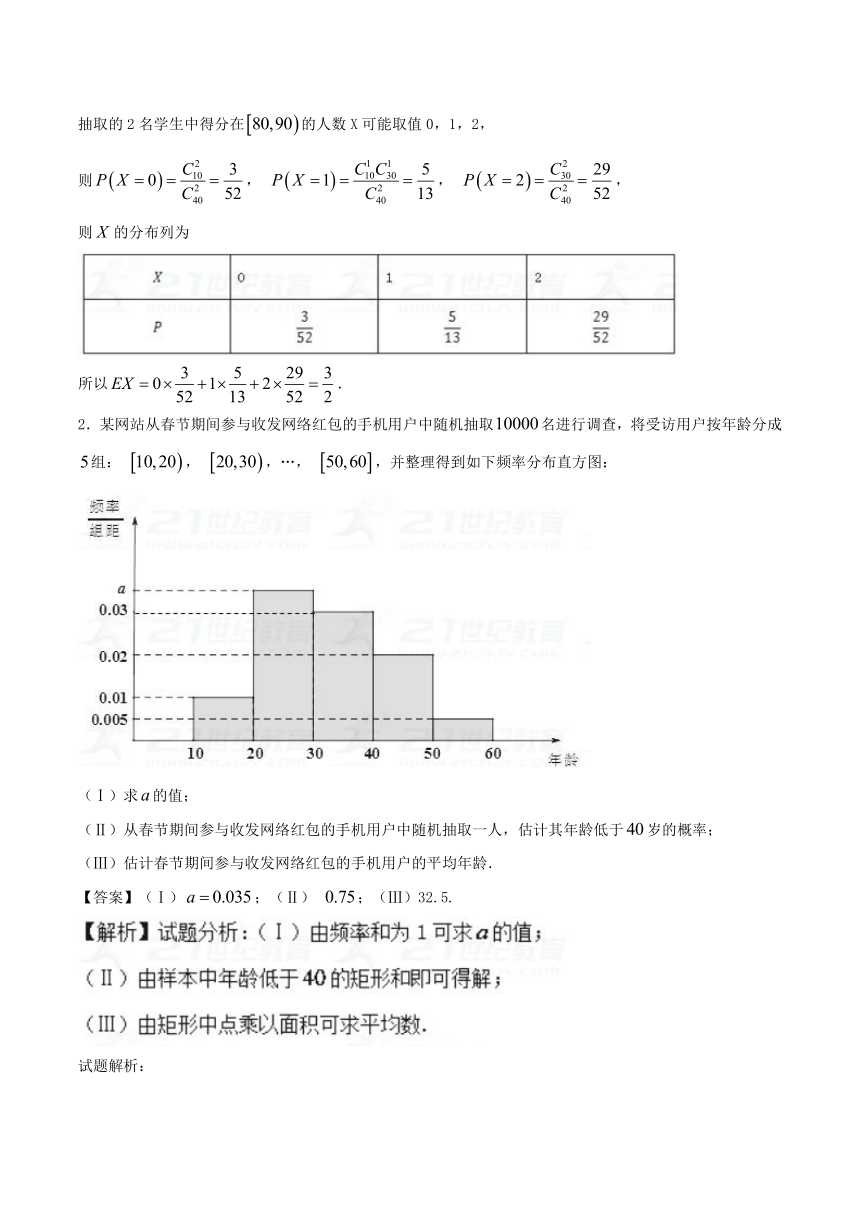
2.某网站从春节期间参与收发网络红包的手机用户中随机抽取名进行调查,将受访用户按年龄分成组: , ,…, ,并整理得到如下频率分布直方图:
(Ⅰ)求的值;
(Ⅱ)从春节期间参与收发网络红包的手机用户中随机抽取一人,估计其年龄低于岁的概率;
(Ⅲ)估计春节期间参与收发网络红包的手机用户的平均年龄.
【答案】(Ⅰ);(Ⅱ) ;(Ⅲ)32.5.
试题解析:
(Ⅰ) 根据频率分布直方图可知, ,
解得.
(Ⅱ)根据题意,样本中年龄低于的频率为
,
所以从春节期间参与收发网络红包的手机用户中随机抽取一人,
估计其年龄低于40岁的概率为.
(Ⅲ)根据题意,春节期间参与收发网络红包的手机用户的平均年龄估计为
(岁).
3.为了弘扬民族文化,某中学举行了“我爱国学,传诵经典”考试,并从中随机抽取了60名学生的成绩(满分100分)作为样本,其中成绩不低于80分的学生被评为优秀生,得到成绩分布的频率分布直方图如图所示.
(1)若该所中学共有2000名学生,试利用样本估计全校这次考试中优秀生人数;
(2)(i)试估计这次参加考试的学生的平均成绩(同一组数据用该组区间的中点值作代表);
(ii)若在样本中,利用分层抽样的方法从成绩不低于70分的学生中随机抽取6人,再从中抽取3人赠送一套国学经典学籍,试求恰好抽中2名优秀生的概率.
【答案】(1)600;(2)(i)72.5;(ii).
试题解析;(1)由直方图可知,样本中数据落在的频率为,
则估计全校这次考试中优秀生人数为.
(2)(i)设样本数据的平均数为,
则,
则估计所有参加考试的学生的平均成绩为72.5.
所以恰好抽中2名优秀生的概率为.
【点睛】
统计中的四个数据特征
(1)众数:在样本数据中,出现次数最多的那个数据.
(2)中位数:样本数据中,将数据按大小排列,位于最中间的数据.如果数据的个数为偶数,就取中间两个数据的平均数作为中位数.
(3)平均数:样本数据的算术平均数,即= (x1+x2+…+xn).
(其中频率分布直方图中,用每组数据中点数表示)
(4)方差与标准差.
s2= [(x1-)2+(x2-)2+…+(xn-)2],
4.2018年中央电视台春节联欢晚会分会场之一落户黔东南州黎平县肇兴侗寨,黔东南州某中学高二社会实践小组就社区群众春晚节目的关注度进行了调查,随机抽取80名群众进行调查,将他们的年龄分成6段: ,,,, , ,得到如图所示的频率分布直方图.
(Ⅰ)求这80名群众年龄的中位数;
(Ⅱ)将频率视为概率,现用随机抽样方法从该社区群众中每次抽取1人,共抽取3次,记被抽取的3人中年龄在的人数为,若每次抽取的结果是相互独立的,求的分布列,及数学期望.
【答案】(Ⅰ)55;(Ⅱ)答案见解析.
【解析】试题分析: 设名群众年龄的中位数为,根据频率分布直方图数据即可求出的值,即名群众年龄的中位数求出年龄在的概率,由题意可知, 的所有可能取值为,求出相对应的概率,即可求得的分布列,及数学期望
(Ⅱ)由频率分布直方图可知,任意抽取1名群众,年龄恰在的概率为,
由题意可知, 的所有可能取值为0,1,2,3,
,
的分布列为
0
1
2
3
所以.或者
5.树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站退出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组,第2组,第3组,第4组,第5组,得到的频率分布直方图如图所示.
(1)求出的值;
(2)求这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(3)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求这2组恰好抽到2人的概率.
【答案】(1)(2)平均数为41.5,中位数为(3)
5人中随机抽取3人,共10个基本事件,从而得到第2组中抽到2人的概率.
试题解析:
(1)由,得.
(2)平均数为;岁;
设中位数为,则 岁.
(3)第1,2,3组的人数分别为20人,30人,从第1,2组中用分层抽样的方法抽取5人,则第1,2组抽取的人数分别为2人,3人,分别记为.
设从5人中随机抽取3人,为,
共10个基本事件,从而第2组中抽到2人的概率.
6.某地区工会利用 “健步行APP”开展健步走积分奖励活动.会员每天走5千步可获积分30分(不足5千步不积分),每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了1000名会员,统计了当天他们的步数,并将样本数据分为, , , , , , , , 九组,整理得到如下频率分布直方图:
(Ⅰ)求当天这1000名会员中步数少于11千步的人数;
(Ⅱ)从当天步数在, , 的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
(Ⅲ)写出该组数据的中位数(只写结果).
【答案】(1) 300人;(2) ;(3) .
【解析】试题分析:(1)根据条形分布直方图中的数据得到健步走的步数在内的人数为,
在内的人数为,在内的人数为,共得到300人;(2)根据分层抽样的概念得到在内应抽取3人,每人的积分是90分,在内应抽取2人,每人的积分是110分,在内应抽取1人,每人的积分是130分,再根据古典概型的公式得到概率值;(3)由中位数的概念,根据直方图可求出结果.
解析:
(Ⅰ)这1000名会员中健步走的步数在内的人数为;
健步走的步数在内的人数为;
健步走的步数在内的人数为;
健步走的步数在内的人数为;
.
所以这1000名会员中健步走的步数少于11千步的人数为300人.
从6人中随机抽取2人,有, , , , , , , , , ,
, , , , 共15种方法.
所以从6人中随机抽取2人,这2人的积分之和不少于200分的有, , ,
, , , , , , , , 共12种方法.
设从6人中随机抽取2人,这2人的积分之和不少于200分为事件,则
.
所以从6人中随机抽取2人,这2人的积分之和不少于200分的概率为.
(Ⅲ)中位数为.
第三篇 概率与统计专题05 频率分布直方图与数字特征
1.为选拔选手参加“中国诗词大会”,某中学举行一次“诗词大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为)进行统计.按照, , , , 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在, 的数据).
(1)求样本容量和频率分布直方图中、的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“中国谜语大会”,设随机变量表示所抽取的2名学生中得分在内的学生人数,求随机变量的分布列及数学期望.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)由频率分布直方图及题意可得样本容量与、的值;(2)抽取的2名学生中得分在的人数X可能取值0,1,2,求出相应的概率值,即可得到随机变量的分布列及数学期望.
抽取的2名学生中得分在的人数X可能取值0,1,2,
则, , ,
则的分布列为
所以.
2.某网站从春节期间参与收发网络红包的手机用户中随机抽取名进行调查,将受访用户按年龄分成组: , ,…, ,并整理得到如下频率分布直方图:
(Ⅰ)求的值;
(Ⅱ)从春节期间参与收发网络红包的手机用户中随机抽取一人,估计其年龄低于岁的概率;
(Ⅲ)估计春节期间参与收发网络红包的手机用户的平均年龄.
【答案】(Ⅰ);(Ⅱ) ;(Ⅲ)32.5.
试题解析:
(Ⅰ) 根据频率分布直方图可知, ,
解得.
(Ⅱ)根据题意,样本中年龄低于的频率为
,
所以从春节期间参与收发网络红包的手机用户中随机抽取一人,
估计其年龄低于40岁的概率为.
(Ⅲ)根据题意,春节期间参与收发网络红包的手机用户的平均年龄估计为
(岁).
3.为了弘扬民族文化,某中学举行了“我爱国学,传诵经典”考试,并从中随机抽取了60名学生的成绩(满分100分)作为样本,其中成绩不低于80分的学生被评为优秀生,得到成绩分布的频率分布直方图如图所示.
(1)若该所中学共有2000名学生,试利用样本估计全校这次考试中优秀生人数;
(2)(i)试估计这次参加考试的学生的平均成绩(同一组数据用该组区间的中点值作代表);
(ii)若在样本中,利用分层抽样的方法从成绩不低于70分的学生中随机抽取6人,再从中抽取3人赠送一套国学经典学籍,试求恰好抽中2名优秀生的概率.
【答案】(1)600;(2)(i)72.5;(ii).
试题解析;(1)由直方图可知,样本中数据落在的频率为,
则估计全校这次考试中优秀生人数为.
(2)(i)设样本数据的平均数为,
则,
则估计所有参加考试的学生的平均成绩为72.5.
所以恰好抽中2名优秀生的概率为.
【点睛】
统计中的四个数据特征
(1)众数:在样本数据中,出现次数最多的那个数据.
(2)中位数:样本数据中,将数据按大小排列,位于最中间的数据.如果数据的个数为偶数,就取中间两个数据的平均数作为中位数.
(3)平均数:样本数据的算术平均数,即= (x1+x2+…+xn).
(其中频率分布直方图中,用每组数据中点数表示)
(4)方差与标准差.
s2= [(x1-)2+(x2-)2+…+(xn-)2],
4.2018年中央电视台春节联欢晚会分会场之一落户黔东南州黎平县肇兴侗寨,黔东南州某中学高二社会实践小组就社区群众春晚节目的关注度进行了调查,随机抽取80名群众进行调查,将他们的年龄分成6段: ,,,, , ,得到如图所示的频率分布直方图.
(Ⅰ)求这80名群众年龄的中位数;
(Ⅱ)将频率视为概率,现用随机抽样方法从该社区群众中每次抽取1人,共抽取3次,记被抽取的3人中年龄在的人数为,若每次抽取的结果是相互独立的,求的分布列,及数学期望.
【答案】(Ⅰ)55;(Ⅱ)答案见解析.
【解析】试题分析: 设名群众年龄的中位数为,根据频率分布直方图数据即可求出的值,即名群众年龄的中位数求出年龄在的概率,由题意可知, 的所有可能取值为,求出相对应的概率,即可求得的分布列,及数学期望
(Ⅱ)由频率分布直方图可知,任意抽取1名群众,年龄恰在的概率为,
由题意可知, 的所有可能取值为0,1,2,3,
,
的分布列为
0
1
2
3
所以.或者
5.树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站退出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组,第2组,第3组,第4组,第5组,得到的频率分布直方图如图所示.
(1)求出的值;
(2)求这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(3)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求这2组恰好抽到2人的概率.
【答案】(1)(2)平均数为41.5,中位数为(3)
5人中随机抽取3人,共10个基本事件,从而得到第2组中抽到2人的概率.
试题解析:
(1)由,得.
(2)平均数为;岁;
设中位数为,则 岁.
(3)第1,2,3组的人数分别为20人,30人,从第1,2组中用分层抽样的方法抽取5人,则第1,2组抽取的人数分别为2人,3人,分别记为.
设从5人中随机抽取3人,为,
共10个基本事件,从而第2组中抽到2人的概率.
6.某地区工会利用 “健步行APP”开展健步走积分奖励活动.会员每天走5千步可获积分30分(不足5千步不积分),每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了1000名会员,统计了当天他们的步数,并将样本数据分为, , , , , , , , 九组,整理得到如下频率分布直方图:
(Ⅰ)求当天这1000名会员中步数少于11千步的人数;
(Ⅱ)从当天步数在, , 的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
(Ⅲ)写出该组数据的中位数(只写结果).
【答案】(1) 300人;(2) ;(3) .
【解析】试题分析:(1)根据条形分布直方图中的数据得到健步走的步数在内的人数为,
在内的人数为,在内的人数为,共得到300人;(2)根据分层抽样的概念得到在内应抽取3人,每人的积分是90分,在内应抽取2人,每人的积分是110分,在内应抽取1人,每人的积分是130分,再根据古典概型的公式得到概率值;(3)由中位数的概念,根据直方图可求出结果.
解析:
(Ⅰ)这1000名会员中健步走的步数在内的人数为;
健步走的步数在内的人数为;
健步走的步数在内的人数为;
健步走的步数在内的人数为;
.
所以这1000名会员中健步走的步数少于11千步的人数为300人.
从6人中随机抽取2人,有, , , , , , , , , ,
, , , , 共15种方法.
所以从6人中随机抽取2人,这2人的积分之和不少于200分的有, , ,
, , , , , , , , 共12种方法.
设从6人中随机抽取2人,这2人的积分之和不少于200分为事件,则
.
所以从6人中随机抽取2人,这2人的积分之和不少于200分的概率为.
(Ⅲ)中位数为.
同课章节目录
