2018年高考数学百强校大题狂练系列(通用版)专题3.3+回归分析
文档属性
| 名称 | 2018年高考数学百强校大题狂练系列(通用版)专题3.3+回归分析 |  | |
| 格式 | zip | ||
| 文件大小 | 764.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-25 15:24:26 | ||
图片预览



文档简介
2018届高考数学大题狂练
第三篇 概率与统计 专题03 回归分析
1.某印刷厂为了研究单册书籍的成本(单位:元)与印刷册数(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲: ,方程乙: .
(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到0.1);
②分别计算模型甲与模型乙的残差平方和及,并通过比较的大小,判断哪个模型拟合效果更好.
(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷,根据市场调查,新需求量为10千册,若印刷厂以每册5元的价格将书籍出售给订货商,求印刷厂二次印刷10千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
【答案】(1)①.答案见解析;②.答案见解析;(2)33360元.
试题解析:
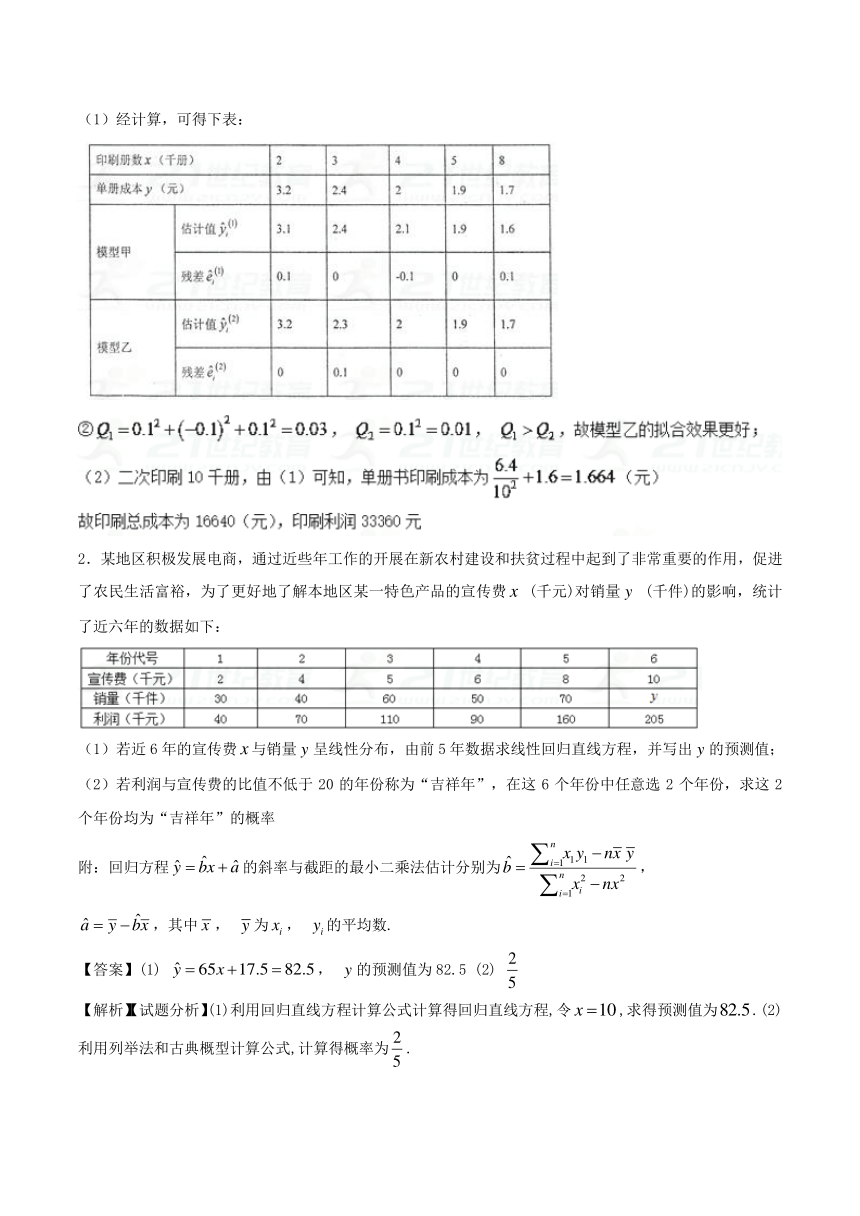
(1)经计算,可得下表:
2.某地区积极发展电商,通过近些年工作的开展在新农村建设和扶贫过程中起到了非常重要的作用,促进了农民生活富裕,为了更好地了解本地区某一特色产品的宣传费 (千元)对销量 (千件)的影响,统计了近六年的数据如下:
(1)若近6年的宣传费与销量呈线性分布,由前5年数据求线性回归直线方程,并写出的预测值;
(2)若利润与宣传费的比值不低于20的年份称为“吉祥年”,在这6个年份中任意选2个年份,求这2个年份均为“吉祥年”的概率
附:回归方程的斜率与截距的最小二乘法估计分别为,
,其中, 为, 的平均数.
【答案】(1) , 的预测值为82.5 (2)
【解析】【试题分析】(1)利用回归直线方程计算公式计算得回归直线方程,令,求得预测值为.(2)利用列举法和古典概型计算公式,计算得概率为.
∴
∴回归直线方程为,将代入得
∴的预测值为82.5.
(2)从6个年份中任取2个年份的情况为: , , , , , , , , , , , , , , ,共15种.
2个年份均为“吉祥年”的情况有: , , , , , ,共6种.
∴6个年份中任意选个2个年份均为“吉祥年”的概率为.
3.已知鸡的产蛋量与鸡舍的温度有关,为了确定下一个时段鸡舍的控制温度,某企业需要了解鸡舍的温度(单位),对某种鸡的时段产蛋量(单位: )和时段投入成本(单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度和产蛋量的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
其中, .
(1)根据散点图判断, 与哪一个更适宜作为该种鸡的时段产蛋量关于鸡舍时段控制温度的回归方程类型?(给判断即可,不必说明理由)
(2)若用作为回归方程模型,根据表中数据,建立关于的回归方程;
(3)已知时段投入成本与的关系为,当时段控制温度为时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
附:①对于一组具有线性相关关系的数据,其回归直线的斜率和截距的最小二乘估计分别为,
②
【答案】(1)适宜;(2);(3)48.432.
线方程得到时, , .
试题解析:
(1)适宜
∴关于的回归方程为
(3)时,由回归方程得,
即鸡舍的温度为时,鸡的时段产量的预报值为515.4,投入成本的预报值为48.432.
4.某地区某农产品近几年的产量统计如下表:
(1)根据表中数据,建立关于的线性回归方程;
(2)若近几年该农产品每千克的价格 (单位:元)与年产量满足的函数关系式为,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区年该农产品的产量;
②当为何值时,销售额最大?
附:对于一组数据,其回归直线的斜率和截距的最小二乘估计分别为: , .
【答案】(1)(2)①7. 56②
【解析】【试题分析】(1)将数据代入回归直线方程计算公式,可求得回归直线方程.(2)①将代入(1)所求得方程,可求得对应的预测值. ②求得销售额的表达式为,利用二次函数对称轴可求得其最大值.
【试题解析】
解:(1)由题, , ,
,
所以,又,得,
所以关于的线性回归方程为.
当时,函数取得最大值,又因,
计算得当,即时,即2018年销售额最大.
5.一只药用昆虫的产卵数y与一定范围内的温度x有关, 现收集了该种药用昆虫的6组观测数据如下表:
温度x/?C
21
23
24
27
29
32
产卵数y/个
6
11
20
27
57
77
经计算得: , , , ,
,线性回归模型的残差平方和,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
(Ⅰ)若用线性回归模型,求y关于x的回归方程=x+(精确到0.1);
(Ⅱ)若用非线性回归模型求得y关于x的回归方程为=0.06e0.2303x,且相关指数R2=0.9522.
( i )试与 (Ⅰ)中的回归模型相比,用R2说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为35?C时该种药用昆虫的产卵数(结果取整数).
附:一组数据(x1,y1), (x2,y2), ...,(xn,yn ), 其回归直线=x+的斜率和截距的最小二乘估计为
=?;相关指数R2=.
【答案】(Ⅰ) =6.6x?138.6.(Ⅱ)(i)答案见解析;(2)190.
【解析】试题分析:
试题解析:
(Ⅰ)由题意得,
∴33?6.6?26=?138.6,
∴y关于x的线性回归方程为=6.6x?138.6.
(Ⅱ) ( i )由所给数据求得的线性回归方程为=6.6x?138.6,相关指数为
R2=
因为0.9398<0.9522,
所以回归方程=0.06e0.2303x比线性回归方程=6.6x?138.6拟合效果更好.
( ii )由( i )得当温度x=35?C时, =0.06e0.2303?35=0.06?e8.0605.
又∵e8.0605≈3167,
∴≈0.06?3167≈190(个).
即当温度x=35?C时,该种药用昆虫的产卵数估计为190个.
点睛:
(1)回归分析问题中的计算比较复杂,因此在解题时要充分利用条件中所给的已知数据和公式.
(2)回归分析方程刻画了变量之间相关关系的相关程度,回归方程的不同,其反映的拟合效果也不一样,对此可用相关指数R2来刻画回归方程的拟合效果.对同一组变量得到的不同的回归方程,当相关指数R2越大时,其拟合效果越好.
6.在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差x(单位:分)与物理偏差y(单位:分)之间的关系进行学科偏差分析,决定从全班56位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
学生序号
1
2
3
4
5
6
7
8
数学偏差x
20
15
13
3
2
-5
-10
-18
物理偏差y
6.5
3.5
3.5
1.5
0.5
-0.5
-2.5
-3.5
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;
(2)若这次考试该班数学平均分为118分,物理平均分为90.5,试预测数学成绩126分的同学的物理成绩.
参考公式: .
参考数据: .
【答案】(1) ;(2) 分.
试题解析:
(1)由题意,
计算==,
==,
所以=-=-×=,
所以线性回归方程为=x+.
(2)由题意,设该同学的物理成绩为w,则物理偏差为w-90.5,
又该同学的数学偏差为126-118=8.
由(1)中回归方程,得w-90.5=×8+,解得w=93.
所以,能够预测这位同学的物理成绩为93分.
第三篇 概率与统计 专题03 回归分析
1.某印刷厂为了研究单册书籍的成本(单位:元)与印刷册数(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲: ,方程乙: .
(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到0.1);
②分别计算模型甲与模型乙的残差平方和及,并通过比较的大小,判断哪个模型拟合效果更好.
(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷,根据市场调查,新需求量为10千册,若印刷厂以每册5元的价格将书籍出售给订货商,求印刷厂二次印刷10千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
【答案】(1)①.答案见解析;②.答案见解析;(2)33360元.
试题解析:
(1)经计算,可得下表:
2.某地区积极发展电商,通过近些年工作的开展在新农村建设和扶贫过程中起到了非常重要的作用,促进了农民生活富裕,为了更好地了解本地区某一特色产品的宣传费 (千元)对销量 (千件)的影响,统计了近六年的数据如下:
(1)若近6年的宣传费与销量呈线性分布,由前5年数据求线性回归直线方程,并写出的预测值;
(2)若利润与宣传费的比值不低于20的年份称为“吉祥年”,在这6个年份中任意选2个年份,求这2个年份均为“吉祥年”的概率
附:回归方程的斜率与截距的最小二乘法估计分别为,
,其中, 为, 的平均数.
【答案】(1) , 的预测值为82.5 (2)
【解析】【试题分析】(1)利用回归直线方程计算公式计算得回归直线方程,令,求得预测值为.(2)利用列举法和古典概型计算公式,计算得概率为.
∴
∴回归直线方程为,将代入得
∴的预测值为82.5.
(2)从6个年份中任取2个年份的情况为: , , , , , , , , , , , , , , ,共15种.
2个年份均为“吉祥年”的情况有: , , , , , ,共6种.
∴6个年份中任意选个2个年份均为“吉祥年”的概率为.
3.已知鸡的产蛋量与鸡舍的温度有关,为了确定下一个时段鸡舍的控制温度,某企业需要了解鸡舍的温度(单位),对某种鸡的时段产蛋量(单位: )和时段投入成本(单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度和产蛋量的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
其中, .
(1)根据散点图判断, 与哪一个更适宜作为该种鸡的时段产蛋量关于鸡舍时段控制温度的回归方程类型?(给判断即可,不必说明理由)
(2)若用作为回归方程模型,根据表中数据,建立关于的回归方程;
(3)已知时段投入成本与的关系为,当时段控制温度为时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
附:①对于一组具有线性相关关系的数据,其回归直线的斜率和截距的最小二乘估计分别为,
②
【答案】(1)适宜;(2);(3)48.432.
线方程得到时, , .
试题解析:
(1)适宜
∴关于的回归方程为
(3)时,由回归方程得,
即鸡舍的温度为时,鸡的时段产量的预报值为515.4,投入成本的预报值为48.432.
4.某地区某农产品近几年的产量统计如下表:
(1)根据表中数据,建立关于的线性回归方程;
(2)若近几年该农产品每千克的价格 (单位:元)与年产量满足的函数关系式为,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区年该农产品的产量;
②当为何值时,销售额最大?
附:对于一组数据,其回归直线的斜率和截距的最小二乘估计分别为: , .
【答案】(1)(2)①7. 56②
【解析】【试题分析】(1)将数据代入回归直线方程计算公式,可求得回归直线方程.(2)①将代入(1)所求得方程,可求得对应的预测值. ②求得销售额的表达式为,利用二次函数对称轴可求得其最大值.
【试题解析】
解:(1)由题, , ,
,
所以,又,得,
所以关于的线性回归方程为.
当时,函数取得最大值,又因,
计算得当,即时,即2018年销售额最大.
5.一只药用昆虫的产卵数y与一定范围内的温度x有关, 现收集了该种药用昆虫的6组观测数据如下表:
温度x/?C
21
23
24
27
29
32
产卵数y/个
6
11
20
27
57
77
经计算得: , , , ,
,线性回归模型的残差平方和,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
(Ⅰ)若用线性回归模型,求y关于x的回归方程=x+(精确到0.1);
(Ⅱ)若用非线性回归模型求得y关于x的回归方程为=0.06e0.2303x,且相关指数R2=0.9522.
( i )试与 (Ⅰ)中的回归模型相比,用R2说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为35?C时该种药用昆虫的产卵数(结果取整数).
附:一组数据(x1,y1), (x2,y2), ...,(xn,yn ), 其回归直线=x+的斜率和截距的最小二乘估计为
=?;相关指数R2=.
【答案】(Ⅰ) =6.6x?138.6.(Ⅱ)(i)答案见解析;(2)190.
【解析】试题分析:
试题解析:
(Ⅰ)由题意得,
∴33?6.6?26=?138.6,
∴y关于x的线性回归方程为=6.6x?138.6.
(Ⅱ) ( i )由所给数据求得的线性回归方程为=6.6x?138.6,相关指数为
R2=
因为0.9398<0.9522,
所以回归方程=0.06e0.2303x比线性回归方程=6.6x?138.6拟合效果更好.
( ii )由( i )得当温度x=35?C时, =0.06e0.2303?35=0.06?e8.0605.
又∵e8.0605≈3167,
∴≈0.06?3167≈190(个).
即当温度x=35?C时,该种药用昆虫的产卵数估计为190个.
点睛:
(1)回归分析问题中的计算比较复杂,因此在解题时要充分利用条件中所给的已知数据和公式.
(2)回归分析方程刻画了变量之间相关关系的相关程度,回归方程的不同,其反映的拟合效果也不一样,对此可用相关指数R2来刻画回归方程的拟合效果.对同一组变量得到的不同的回归方程,当相关指数R2越大时,其拟合效果越好.
6.在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差x(单位:分)与物理偏差y(单位:分)之间的关系进行学科偏差分析,决定从全班56位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
学生序号
1
2
3
4
5
6
7
8
数学偏差x
20
15
13
3
2
-5
-10
-18
物理偏差y
6.5
3.5
3.5
1.5
0.5
-0.5
-2.5
-3.5
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;
(2)若这次考试该班数学平均分为118分,物理平均分为90.5,试预测数学成绩126分的同学的物理成绩.
参考公式: .
参考数据: .
【答案】(1) ;(2) 分.
试题解析:
(1)由题意,
计算==,
==,
所以=-=-×=,
所以线性回归方程为=x+.
(2)由题意,设该同学的物理成绩为w,则物理偏差为w-90.5,
又该同学的数学偏差为126-118=8.
由(1)中回归方程,得w-90.5=×8+,解得w=93.
所以,能够预测这位同学的物理成绩为93分.
同课章节目录
