人教版初中数学七年级下册第九章《9.1不等式》同步练习题(含答案)
文档属性
| 名称 | 人教版初中数学七年级下册第九章《9.1不等式》同步练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 114.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-28 20:51:10 | ||
图片预览

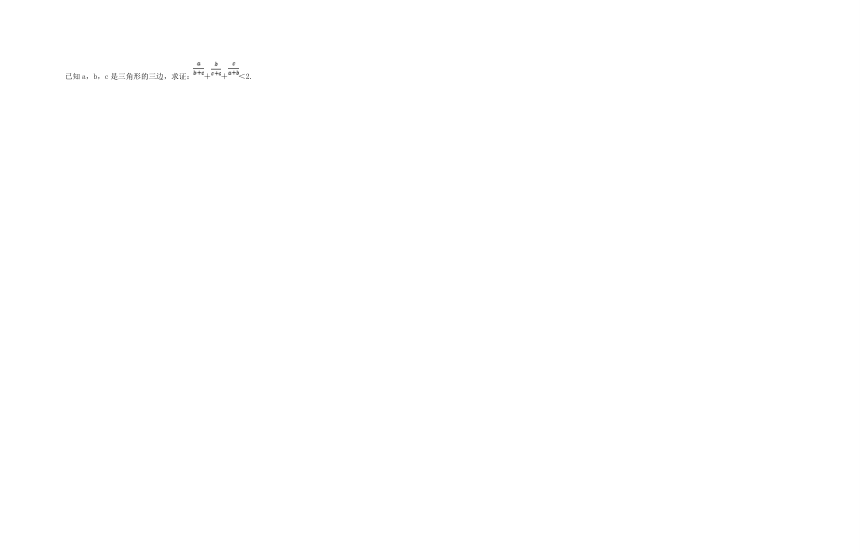
文档简介
《9.1不等式》同步练习题
一、选择题(每小题只有一个正确答案)
1.下列式子:(1)4>0;(2)2x+3y<0;(3)x=3;(4)x≠y;(5)x+y;(6)x+3≤7中,不等式的个数有( )
A. 2个 B. 3个 C. 4个 D. 5个
2.若a<b<0,则下列各式错误的是(?? )
A. a﹣2<b﹣2?????????? B. ????????????????????? C. ??????? D. 2a﹣1<2b﹣1
3.在-2,-1,0,1,2中,不等式x+3>2的解有( )
A. 1个 B. 2个 C. 3个 D. 4个
4.若,那么下列各式中正确的是( )
A. mp>np B. n25.如果,则下列不等式成立的( )
A. B. C. D.
6.设“●”“▲”“■”表示三种不同的物体,现用天平称了两次,情况如图所示,那么这三种物体的质量按从大到小的顺序排列应为( )
A. ■●▲ B. ●▲■ C. ■▲● D. ▲■●
7.7.b<0时,比较a,a-b,a+b的大小,正确的是( )
A. a-b>a>a+b B. a-b>a+b>a
C. a+b>a-b>a D. a>a-b>a+b
二、填空题
8.已知关于x的不等式3x-5k>-7的解集是x>1,则k的值为________.
9.若a10.用不等式样表示:
(1)与的差是一个负数:_____;(2)的不小于与3的差:_____.
11.用适当的符号表示下列关系:
(1)a-b是负数:________;
(2)a比5大:________;
(3)x是非负数:_______;
(4)m不大于-3:_________.
12.下列结论正确的有__________(填序号).
①如果,;那么 ②如果;那么 ③如果,那么;
④如果,那么.
三、解答题
13.把下列不等式的解集在数轴上表示出来.
(1)x≥-3;(2)x>-1;(3)x≤3;(4)x<-.
14.利用不等式的基本性质,将下列不等式化为或的形式:
(1);(2).
15.阅读材料:
(1)若x>y>0,且m>0,则有<;
(2)若a<b,c<d,则有a+c<b+d.
请依据以上材料解答问题:
已知a,b,c是三角形的三边,求证:++<2.
参考答案
1.C
【解析】根据不等式的定义,只要有不等符号的式子就是不等式, 所以(1),(2),(4),(6)为不等式,共有4个. 故选C.
2.B
【解析】∵a<b<0,
∴(1)a-2(2),即B不成立;
(3),即C成立;
(4),即D成立.
故选B.
3.C
【解析】-2+3=1<2,不是不等式x+3>2的解;-1+3=2,不是不等式x+3>2的解;0+3=3>2,是不等式x+3>2的解;1+3=4>2,是不等式x+3>2的解;2+3=5>2,是不等式x+3>2的解;
所以不等式的解有3个,
故选C.
4.B
【解析】因为,根据不等式的性质,得n2故选B.
5.B
【解析】试题解析: ∵
∴(不等式两边同时乘以同一个大于0的数,不等号方向不变);
(不等式两边同时除以同一个大于0的数,不等号方向不变);
∴
故选B.
6.C
【解析】依图①得:2■=■+▲,即■=▲,依图②得到●+ ●+ ●=▲+ ●,即●+ ●=▲,故有:■>▲>●. 故选:C.
7.A
【解析】由于b<0,则-b>0,于是有a>a+b,a-b>a,所以a-b>a>a+b. 故选:A.
8.2
【解析】试题分析:不等式可变形为:3x>5k-7,
x>,
∵关于x的不等式3x-5k>-7的解集是x>1,
∴=1,
解得:k=2.
故答案为:2.
9.1<1-b<1-a
【解析】试题解析:∵
∴
∴
所以由小到大的顺序用“<”连接起来为:
故答案为:
10.
【解析】试题解析:根据题意可得:
(1). , (2). .
故答案为:(1). , (2). .
11. a-b<0 a>5 x≥0 m≤-3
【解析】(1)“a-b是负数”用不等式表示为:a-b<0;
(2)“a比5大”用不等式表示为:a>5;
(3)“x是非负数”用不等式表示为: ;
(4)“m不大于-3”用不等式表示为: .
故答案为:(1). a-b<0 (2). a>5 (3). x≥0 (4). m≤-3.
12.①④
【解析】试题解析:①∵,
∴,
∵,
∴,
故①正确.
②当时,,
故②错.
③若,,满足,但,
故③错.
④∵,
∴,
∴,
故④正确.
故答案为:①④.
13.(1)
(2)
(3)
(4)
【解析】试题分析:
将上述不等式的解集规范的表示在数轴上即可.
试题解析:
(1)将表示在数轴上为:
(2)将表示在数轴上为:
(3)将表示在数轴上为:
(4)将表示在数轴上为:
14.(1) x>-; (2) x>6.
【解析】试题分析:(1)根据不等式的性质,计算即可求解;
(2)根据不等式的性质,计算即可求解
试题解析:(1)两边同除以3,得
x>-
(2)两边同城游3,得
2x>18-x
两边同时加上x,得
2x+x>18
即3x>18
两边同除以3,得
x>6
15.2
【解析】试题分析:根据三角形的三边关系,利用不等式的基本性质解答即可.
试题解析:∵a,b,c是三角形三边,
∴a<b+c.
∴<,①
同理<,②
<,③
由①②③得++<=2.
一、选择题(每小题只有一个正确答案)
1.下列式子:(1)4>0;(2)2x+3y<0;(3)x=3;(4)x≠y;(5)x+y;(6)x+3≤7中,不等式的个数有( )
A. 2个 B. 3个 C. 4个 D. 5个
2.若a<b<0,则下列各式错误的是(?? )
A. a﹣2<b﹣2?????????? B. ????????????????????? C. ??????? D. 2a﹣1<2b﹣1
3.在-2,-1,0,1,2中,不等式x+3>2的解有( )
A. 1个 B. 2个 C. 3个 D. 4个
4.若,那么下列各式中正确的是( )
A. mp>np B. n2
A. B. C. D.
6.设“●”“▲”“■”表示三种不同的物体,现用天平称了两次,情况如图所示,那么这三种物体的质量按从大到小的顺序排列应为( )
A. ■●▲ B. ●▲■ C. ■▲● D. ▲■●
7.7.b<0时,比较a,a-b,a+b的大小,正确的是( )
A. a-b>a>a+b B. a-b>a+b>a
C. a+b>a-b>a D. a>a-b>a+b
二、填空题
8.已知关于x的不等式3x-5k>-7的解集是x>1,则k的值为________.
9.若a
(1)与的差是一个负数:_____;(2)的不小于与3的差:_____.
11.用适当的符号表示下列关系:
(1)a-b是负数:________;
(2)a比5大:________;
(3)x是非负数:_______;
(4)m不大于-3:_________.
12.下列结论正确的有__________(填序号).
①如果,;那么 ②如果;那么 ③如果,那么;
④如果,那么.
三、解答题
13.把下列不等式的解集在数轴上表示出来.
(1)x≥-3;(2)x>-1;(3)x≤3;(4)x<-.
14.利用不等式的基本性质,将下列不等式化为或的形式:
(1);(2).
15.阅读材料:
(1)若x>y>0,且m>0,则有<;
(2)若a<b,c<d,则有a+c<b+d.
请依据以上材料解答问题:
已知a,b,c是三角形的三边,求证:++<2.
参考答案
1.C
【解析】根据不等式的定义,只要有不等符号的式子就是不等式, 所以(1),(2),(4),(6)为不等式,共有4个. 故选C.
2.B
【解析】∵a<b<0,
∴(1)a-2
(3),即C成立;
(4),即D成立.
故选B.
3.C
【解析】-2+3=1<2,不是不等式x+3>2的解;-1+3=2,不是不等式x+3>2的解;0+3=3>2,是不等式x+3>2的解;1+3=4>2,是不等式x+3>2的解;2+3=5>2,是不等式x+3>2的解;
所以不等式的解有3个,
故选C.
4.B
【解析】因为,根据不等式的性质,得n2
5.B
【解析】试题解析: ∵
∴(不等式两边同时乘以同一个大于0的数,不等号方向不变);
(不等式两边同时除以同一个大于0的数,不等号方向不变);
∴
故选B.
6.C
【解析】依图①得:2■=■+▲,即■=▲,依图②得到●+ ●+ ●=▲+ ●,即●+ ●=▲,故有:■>▲>●. 故选:C.
7.A
【解析】由于b<0,则-b>0,于是有a>a+b,a-b>a,所以a-b>a>a+b. 故选:A.
8.2
【解析】试题分析:不等式可变形为:3x>5k-7,
x>,
∵关于x的不等式3x-5k>-7的解集是x>1,
∴=1,
解得:k=2.
故答案为:2.
9.1<1-b<1-a
【解析】试题解析:∵
∴
∴
所以由小到大的顺序用“<”连接起来为:
故答案为:
10.
【解析】试题解析:根据题意可得:
(1). , (2). .
故答案为:(1). , (2). .
11. a-b<0 a>5 x≥0 m≤-3
【解析】(1)“a-b是负数”用不等式表示为:a-b<0;
(2)“a比5大”用不等式表示为:a>5;
(3)“x是非负数”用不等式表示为: ;
(4)“m不大于-3”用不等式表示为: .
故答案为:(1). a-b<0 (2). a>5 (3). x≥0 (4). m≤-3.
12.①④
【解析】试题解析:①∵,
∴,
∵,
∴,
故①正确.
②当时,,
故②错.
③若,,满足,但,
故③错.
④∵,
∴,
∴,
故④正确.
故答案为:①④.
13.(1)
(2)
(3)
(4)
【解析】试题分析:
将上述不等式的解集规范的表示在数轴上即可.
试题解析:
(1)将表示在数轴上为:
(2)将表示在数轴上为:
(3)将表示在数轴上为:
(4)将表示在数轴上为:
14.(1) x>-; (2) x>6.
【解析】试题分析:(1)根据不等式的性质,计算即可求解;
(2)根据不等式的性质,计算即可求解
试题解析:(1)两边同除以3,得
x>-
(2)两边同城游3,得
2x>18-x
两边同时加上x,得
2x+x>18
即3x>18
两边同除以3,得
x>6
15.2
【解析】试题分析:根据三角形的三边关系,利用不等式的基本性质解答即可.
试题解析:∵a,b,c是三角形三边,
∴a<b+c.
∴<,①
同理<,②
<,③
由①②③得++<=2.
