2018年高考数学百强校大题狂练系列(通用版)专题5.6+存在性问题
文档属性
| 名称 | 2018年高考数学百强校大题狂练系列(通用版)专题5.6+存在性问题 |

|
|
| 格式 | zip | ||
| 文件大小 | 701.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-02 00:00:00 | ||
图片预览



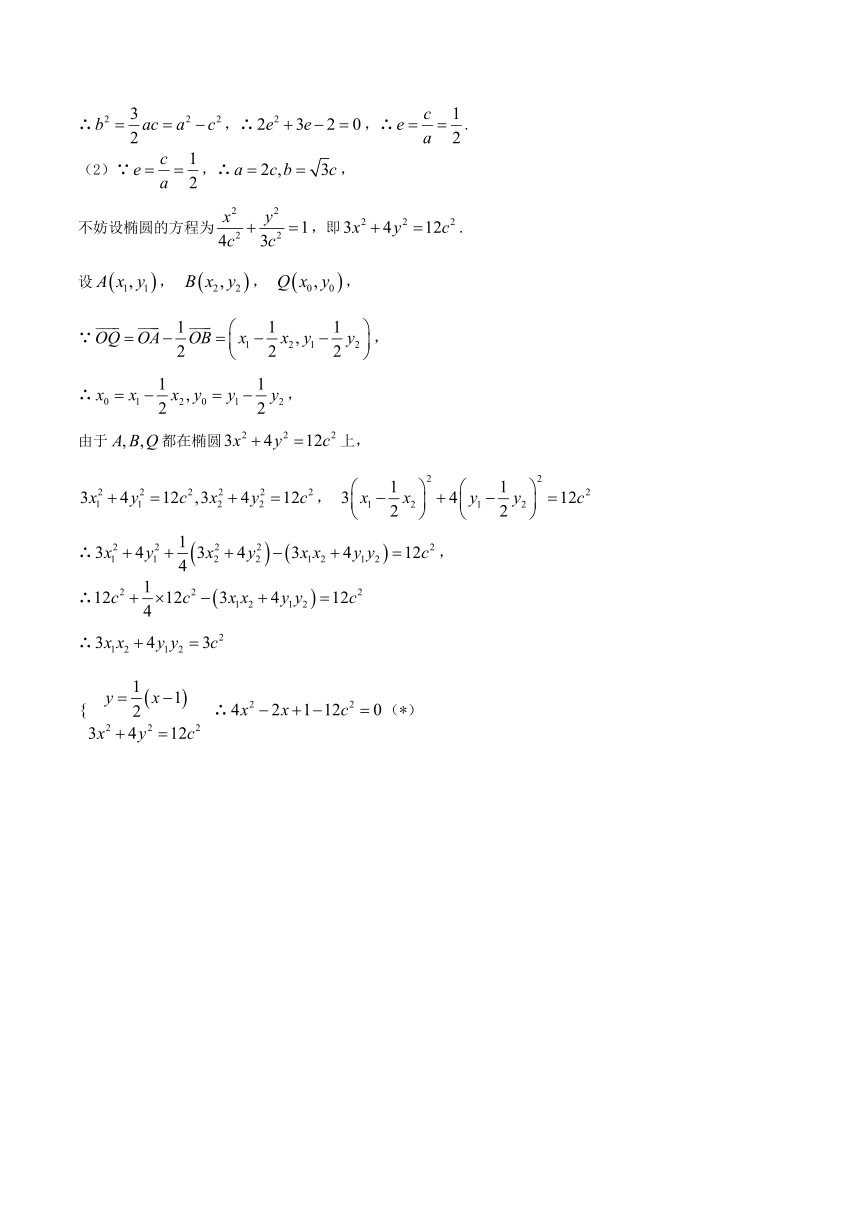
文档简介
2018届高考数学大题狂练
第五篇 解析几何 专题05存在性问题
1.已知椭圆的离心率为,以椭圆的任意三个顶点为顶点的三角形的面积是.
(1)求椭圆的方程;
(2)设是椭圆的右顶点,点在轴上.若椭圆上存在点,使得,求点横坐标的取值范围.
【答案】(1);(2)
【解析】试题分析:(1)设椭圆的半焦距为.依题意,得, ,且.
解得, .由此可得椭圆的方程.
2)“椭圆上存在点,使得”等价于“存在不是椭圆左、右顶点的点,使得成立” 依题意, .设, ,则,且,即.可得,由,解得
点横坐标的取值范围.
(2)“椭圆上存在点,使得”等价于“存在不是椭圆左、右顶点的点,使得成立”.
依题意, .设, ,则,且,
即.
将代入上式,得 .
因为,所以,
即,所以,解得,
所以 点横坐标的取值范围是.
2.已知椭圆:过点和点.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线与椭圆相交于不同的两点, ,是否存在实数,使得?若存在,求出实数;若不存在,请说明理由.
【答案】(1)(2)不存在
解析:(Ⅰ)椭圆:过点和点,
所以,由,解得,
所以椭圆:;
(Ⅱ)假设存在实数满足题设,
由,得,
因为直线与椭圆有两个交点,
所以,即,
设的中点为,分别为点的横坐标,则,
从而,
所以,
因为,
所以,
所以,而,
所以,即,与矛盾,
因此,不存在这样的实数,使得.
3.过椭圆: 的左焦点作其长轴的垂线与的一个交点为,右焦点为,若.
(1)求椭圆的离心率;
(2)过点且斜率为的直线与椭圆交于两点,若椭圆上存在点使得 ,求椭圆的方程.
【答案】(1);(2).
试题解析:
(1)∵,∴,∴,
∴,∴,∴.
(2)∵,∴,
不妨设椭圆的方程为,即.
设, , ,
∵,
∴,
由于都在椭圆上,
,
∴,
∴
∴
∴(*)
4.在直角坐标系中,设点A(-3,0),B(3,0),直线AM,BM相交于点M,且它们的斜率之积是
(1)试讨论点M的轨迹形状;
(2)当0【答案】(1)见解析(2)
【解析】试题分析:(1)设点,根据条件化简,根据方程形式确定轨迹形状,(2)利用两角和表示∠APB,结合斜率公式已经正切和公式表示b的函数,最后根据点的范围确定b的取值范围.
试题解析:((Ⅰ)设点,由题意得:
化简得,所以点的轨迹方程为
(Ⅱ)方法一:当时,设点的坐标为,过点作垂直于轴,垂足为,
因为点P在点M的轨迹上,所以
,
∴
因此的取值范围是
方法二:当时,设点P的坐标为,
∴ 以下同方法一
5.已知点P为曲线C上任意一点, ,直线、的斜率之积为.
(Ⅰ)求曲线的轨迹方程;;
(Ⅱ)是否存在过点的直线与椭圆交于不同的两点、,使得?若存在,求出直线的方程;若不存在,请说明理由.
【答案】(1)(2)
试题解析:(I)设点,则
整理得:
故曲线的轨迹方程为:
.
(II)假设存在直线满足题意.
显然当直线斜率不存在时,直线与椭圆不相交.
①当直线的斜率时,设直线为:
联立,化简得:
由,解得
设点,,则
取的中点,则,则
6.已知椭圆的左顶点为,右焦点为,点在椭圆上.
(1)求椭圆的方程;
(2)若直线与椭圆交于两点,直线分别与轴交于点,在轴上,是否存在点,使得无论非零实数怎样变化,总有为直角?若存在,求出点的坐标;若不存在,请说明理由.
【答案】(1);(2)存在点,使得无论非零实数怎么变化,总有为直角,点坐标为或.
【解析】试题分析:(1)依题意,,结合点在椭圆上及,即可求得椭圆的方程;(2)设,则,联立直线与椭圆的方程,求得,,根据得所在直线方程,即可分别得到与的坐标,结合为直角,列出等式,即可求解.
试题解析:(1)依题意,.
∵点在上,
∴,
又∵
∴,
∴椭圆方程为
∴所在直线方程为,
∴,
同理可得,,.
∴或
∴存在点,使得无论非零实数怎么变化,总有为直角,点坐标为或.
2018届高考数学大题狂练
第五篇 解析几何 专题05存在性问题
1.已知椭圆的离心率为,以椭圆的任意三个顶点为顶点的三角形的面积是.
(1)求椭圆的方程;
(2)设是椭圆的右顶点,点在轴上.若椭圆上存在点,使得,求点横坐标的取值范围.
【答案】(1);(2)
【解析】试题分析:(1)设椭圆的半焦距为.依题意,得, ,且.
解得, .由此可得椭圆的方程.
2)“椭圆上存在点,使得”等价于“存在不是椭圆左、右顶点的点,使得成立” 依题意, .设, ,则,且,即.可得,由,解得
点横坐标的取值范围.
(2)“椭圆上存在点,使得”等价于“存在不是椭圆左、右顶点的点,使得成立”.
依题意, .设, ,则,且,
即.
将代入上式,得 .
因为,所以,
即,所以,解得,
所以 点横坐标的取值范围是.
2.已知椭圆:过点和点.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线与椭圆相交于不同的两点, ,是否存在实数,使得?若存在,求出实数;若不存在,请说明理由.
【答案】(1)(2)不存在
解析:(Ⅰ)椭圆:过点和点,
所以,由,解得,
所以椭圆:;
(Ⅱ)假设存在实数满足题设,
由,得,
因为直线与椭圆有两个交点,
所以,即,
设的中点为,分别为点的横坐标,则,
从而,
所以,
因为,
所以,
所以,而,
所以,即,与矛盾,
因此,不存在这样的实数,使得.
3.过椭圆: 的左焦点作其长轴的垂线与的一个交点为,右焦点为,若.
(1)求椭圆的离心率;
(2)过点且斜率为的直线与椭圆交于两点,若椭圆上存在点使得 ,求椭圆的方程.
【答案】(1);(2).
试题解析:
(1)∵,∴,∴,
∴,∴,∴.
(2)∵,∴,
不妨设椭圆的方程为,即.
设, , ,
∵,
∴,
由于都在椭圆上,
,
∴,
∴
∴
∴(*)
4.在直角坐标系中,设点A(-3,0),B(3,0),直线AM,BM相交于点M,且它们的斜率之积是
(1)试讨论点M的轨迹形状;
(2)当0【答案】(1)见解析(2)
【解析】试题分析:(1)设点,根据条件化简,根据方程形式确定轨迹形状,(2)利用两角和表示∠APB,结合斜率公式已经正切和公式表示b的函数,最后根据点的范围确定b的取值范围.
试题解析:((Ⅰ)设点,由题意得:
化简得,所以点的轨迹方程为
(Ⅱ)方法一:当时,设点的坐标为,过点作垂直于轴,垂足为,
因为点P在点M的轨迹上,所以
,
∴
因此的取值范围是
方法二:当时,设点P的坐标为,
∴ 以下同方法一
5.已知点P为曲线C上任意一点, ,直线、的斜率之积为.
(Ⅰ)求曲线的轨迹方程;;
(Ⅱ)是否存在过点的直线与椭圆交于不同的两点、,使得?若存在,求出直线的方程;若不存在,请说明理由.
【答案】(1)(2)
试题解析:(I)设点,则
整理得:
故曲线的轨迹方程为:
.
(II)假设存在直线满足题意.
显然当直线斜率不存在时,直线与椭圆不相交.
①当直线的斜率时,设直线为:
联立,化简得:
由,解得
设点,,则
取的中点,则,则
6.已知椭圆的左顶点为,右焦点为,点在椭圆上.
(1)求椭圆的方程;
(2)若直线与椭圆交于两点,直线分别与轴交于点,在轴上,是否存在点,使得无论非零实数怎样变化,总有为直角?若存在,求出点的坐标;若不存在,请说明理由.
【答案】(1);(2)存在点,使得无论非零实数怎么变化,总有为直角,点坐标为或.
【解析】试题分析:(1)依题意,,结合点在椭圆上及,即可求得椭圆的方程;(2)设,则,联立直线与椭圆的方程,求得,,根据得所在直线方程,即可分别得到与的坐标,结合为直角,列出等式,即可求解.
试题解析:(1)依题意,.
∵点在上,
∴,
又∵
∴,
∴椭圆方程为
∴所在直线方程为,
∴,
同理可得,,.
∴或
∴存在点,使得无论非零实数怎么变化,总有为直角,点坐标为或.
第五篇 解析几何 专题05存在性问题
1.已知椭圆的离心率为,以椭圆的任意三个顶点为顶点的三角形的面积是.
(1)求椭圆的方程;
(2)设是椭圆的右顶点,点在轴上.若椭圆上存在点,使得,求点横坐标的取值范围.
【答案】(1);(2)
【解析】试题分析:(1)设椭圆的半焦距为.依题意,得, ,且.
解得, .由此可得椭圆的方程.
2)“椭圆上存在点,使得”等价于“存在不是椭圆左、右顶点的点,使得成立” 依题意, .设, ,则,且,即.可得,由,解得
点横坐标的取值范围.
(2)“椭圆上存在点,使得”等价于“存在不是椭圆左、右顶点的点,使得成立”.
依题意, .设, ,则,且,
即.
将代入上式,得 .
因为,所以,
即,所以,解得,
所以 点横坐标的取值范围是.
2.已知椭圆:过点和点.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线与椭圆相交于不同的两点, ,是否存在实数,使得?若存在,求出实数;若不存在,请说明理由.
【答案】(1)(2)不存在
解析:(Ⅰ)椭圆:过点和点,
所以,由,解得,
所以椭圆:;
(Ⅱ)假设存在实数满足题设,
由,得,
因为直线与椭圆有两个交点,
所以,即,
设的中点为,分别为点的横坐标,则,
从而,
所以,
因为,
所以,
所以,而,
所以,即,与矛盾,
因此,不存在这样的实数,使得.
3.过椭圆: 的左焦点作其长轴的垂线与的一个交点为,右焦点为,若.
(1)求椭圆的离心率;
(2)过点且斜率为的直线与椭圆交于两点,若椭圆上存在点使得 ,求椭圆的方程.
【答案】(1);(2).
试题解析:
(1)∵,∴,∴,
∴,∴,∴.
(2)∵,∴,
不妨设椭圆的方程为,即.
设, , ,
∵,
∴,
由于都在椭圆上,
,
∴,
∴
∴
∴(*)
4.在直角坐标系中,设点A(-3,0),B(3,0),直线AM,BM相交于点M,且它们的斜率之积是
(1)试讨论点M的轨迹形状;
(2)当0
【解析】试题分析:(1)设点,根据条件化简,根据方程形式确定轨迹形状,(2)利用两角和表示∠APB,结合斜率公式已经正切和公式表示b的函数,最后根据点的范围确定b的取值范围.
试题解析:((Ⅰ)设点,由题意得:
化简得,所以点的轨迹方程为
(Ⅱ)方法一:当时,设点的坐标为,过点作垂直于轴,垂足为,
因为点P在点M的轨迹上,所以
,
∴
因此的取值范围是
方法二:当时,设点P的坐标为,
∴ 以下同方法一
5.已知点P为曲线C上任意一点, ,直线、的斜率之积为.
(Ⅰ)求曲线的轨迹方程;;
(Ⅱ)是否存在过点的直线与椭圆交于不同的两点、,使得?若存在,求出直线的方程;若不存在,请说明理由.
【答案】(1)(2)
试题解析:(I)设点,则
整理得:
故曲线的轨迹方程为:
.
(II)假设存在直线满足题意.
显然当直线斜率不存在时,直线与椭圆不相交.
①当直线的斜率时,设直线为:
联立,化简得:
由,解得
设点,,则
取的中点,则,则
6.已知椭圆的左顶点为,右焦点为,点在椭圆上.
(1)求椭圆的方程;
(2)若直线与椭圆交于两点,直线分别与轴交于点,在轴上,是否存在点,使得无论非零实数怎样变化,总有为直角?若存在,求出点的坐标;若不存在,请说明理由.
【答案】(1);(2)存在点,使得无论非零实数怎么变化,总有为直角,点坐标为或.
【解析】试题分析:(1)依题意,,结合点在椭圆上及,即可求得椭圆的方程;(2)设,则,联立直线与椭圆的方程,求得,,根据得所在直线方程,即可分别得到与的坐标,结合为直角,列出等式,即可求解.
试题解析:(1)依题意,.
∵点在上,
∴,
又∵
∴,
∴椭圆方程为
∴所在直线方程为,
∴,
同理可得,,.
∴或
∴存在点,使得无论非零实数怎么变化,总有为直角,点坐标为或.
2018届高考数学大题狂练
第五篇 解析几何 专题05存在性问题
1.已知椭圆的离心率为,以椭圆的任意三个顶点为顶点的三角形的面积是.
(1)求椭圆的方程;
(2)设是椭圆的右顶点,点在轴上.若椭圆上存在点,使得,求点横坐标的取值范围.
【答案】(1);(2)
【解析】试题分析:(1)设椭圆的半焦距为.依题意,得, ,且.
解得, .由此可得椭圆的方程.
2)“椭圆上存在点,使得”等价于“存在不是椭圆左、右顶点的点,使得成立” 依题意, .设, ,则,且,即.可得,由,解得
点横坐标的取值范围.
(2)“椭圆上存在点,使得”等价于“存在不是椭圆左、右顶点的点,使得成立”.
依题意, .设, ,则,且,
即.
将代入上式,得 .
因为,所以,
即,所以,解得,
所以 点横坐标的取值范围是.
2.已知椭圆:过点和点.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线与椭圆相交于不同的两点, ,是否存在实数,使得?若存在,求出实数;若不存在,请说明理由.
【答案】(1)(2)不存在
解析:(Ⅰ)椭圆:过点和点,
所以,由,解得,
所以椭圆:;
(Ⅱ)假设存在实数满足题设,
由,得,
因为直线与椭圆有两个交点,
所以,即,
设的中点为,分别为点的横坐标,则,
从而,
所以,
因为,
所以,
所以,而,
所以,即,与矛盾,
因此,不存在这样的实数,使得.
3.过椭圆: 的左焦点作其长轴的垂线与的一个交点为,右焦点为,若.
(1)求椭圆的离心率;
(2)过点且斜率为的直线与椭圆交于两点,若椭圆上存在点使得 ,求椭圆的方程.
【答案】(1);(2).
试题解析:
(1)∵,∴,∴,
∴,∴,∴.
(2)∵,∴,
不妨设椭圆的方程为,即.
设, , ,
∵,
∴,
由于都在椭圆上,
,
∴,
∴
∴
∴(*)
4.在直角坐标系中,设点A(-3,0),B(3,0),直线AM,BM相交于点M,且它们的斜率之积是
(1)试讨论点M的轨迹形状;
(2)当0
【解析】试题分析:(1)设点,根据条件化简,根据方程形式确定轨迹形状,(2)利用两角和表示∠APB,结合斜率公式已经正切和公式表示b的函数,最后根据点的范围确定b的取值范围.
试题解析:((Ⅰ)设点,由题意得:
化简得,所以点的轨迹方程为
(Ⅱ)方法一:当时,设点的坐标为,过点作垂直于轴,垂足为,
因为点P在点M的轨迹上,所以
,
∴
因此的取值范围是
方法二:当时,设点P的坐标为,
∴ 以下同方法一
5.已知点P为曲线C上任意一点, ,直线、的斜率之积为.
(Ⅰ)求曲线的轨迹方程;;
(Ⅱ)是否存在过点的直线与椭圆交于不同的两点、,使得?若存在,求出直线的方程;若不存在,请说明理由.
【答案】(1)(2)
试题解析:(I)设点,则
整理得:
故曲线的轨迹方程为:
.
(II)假设存在直线满足题意.
显然当直线斜率不存在时,直线与椭圆不相交.
①当直线的斜率时,设直线为:
联立,化简得:
由,解得
设点,,则
取的中点,则,则
6.已知椭圆的左顶点为,右焦点为,点在椭圆上.
(1)求椭圆的方程;
(2)若直线与椭圆交于两点,直线分别与轴交于点,在轴上,是否存在点,使得无论非零实数怎样变化,总有为直角?若存在,求出点的坐标;若不存在,请说明理由.
【答案】(1);(2)存在点,使得无论非零实数怎么变化,总有为直角,点坐标为或.
【解析】试题分析:(1)依题意,,结合点在椭圆上及,即可求得椭圆的方程;(2)设,则,联立直线与椭圆的方程,求得,,根据得所在直线方程,即可分别得到与的坐标,结合为直角,列出等式,即可求解.
试题解析:(1)依题意,.
∵点在上,
∴,
又∵
∴,
∴椭圆方程为
∴所在直线方程为,
∴,
同理可得,,.
∴或
∴存在点,使得无论非零实数怎么变化,总有为直角,点坐标为或.
同课章节目录
