2018年高考数学三轮讲练测核心热点总动员(新课标版)热点02+客观题中的三视图、线性规划、框图
文档属性
| 名称 | 2018年高考数学三轮讲练测核心热点总动员(新课标版)热点02+客观题中的三视图、线性规划、框图 |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-02 13:49:35 | ||
图片预览




文档简介
2017年高考三轮复习系列:讲练测之核心热点 【全国通用版】
热点二 客观题中的三视图、线性规划、框图
【名师精讲指南篇】
【高考真题再现】
1.(2017全国1卷理科7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为().
A. B. C. D.
【答案】B
【解析】由三视图可画出立体图,如图所示,该多面体只有两个相同的梯形的面,
,.故选B.
2.(2107全国2卷理科4)如图所示,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为().
A. B. C. D.
【答案】B
【解析】该几何体可视为一个完整的圆柱减去一个高为6的圆柱的一半,如图所示.
.故选B.
3.【2016全国卷2】右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( ).
A.20π B.24π C.28π D.32π
【答案】C
4.【2016全国卷1】如图所示,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是,则它的表面积是( ).
A. B. C. D.
【答案】A
【解析】由几何体的三视图可知,其是一个球被切掉左上角的后的几何体.表面积是的球面面积和三个扇形面积之和.由,得,所以.因此.故选A.
5.(2017全国1理14)设x,y满足约束条件,则的最小值为.
【答案】-5.
6.(2017全国2理5)设,满足约束条件,则的最小值是().
A. B. C. D.
【答案】A
【解析】目标区域如图所示,当直线过点时,所求取到最小值为.故选A.
7.【2016全国卷3文】设,满足约束条件,则的最小值为______.
【答案】
【解析】可行域为及其内部,其中,直线过点时取最小值.
【答案】
【解析】 可行域如图所示.当直线经过时,取最大值为.
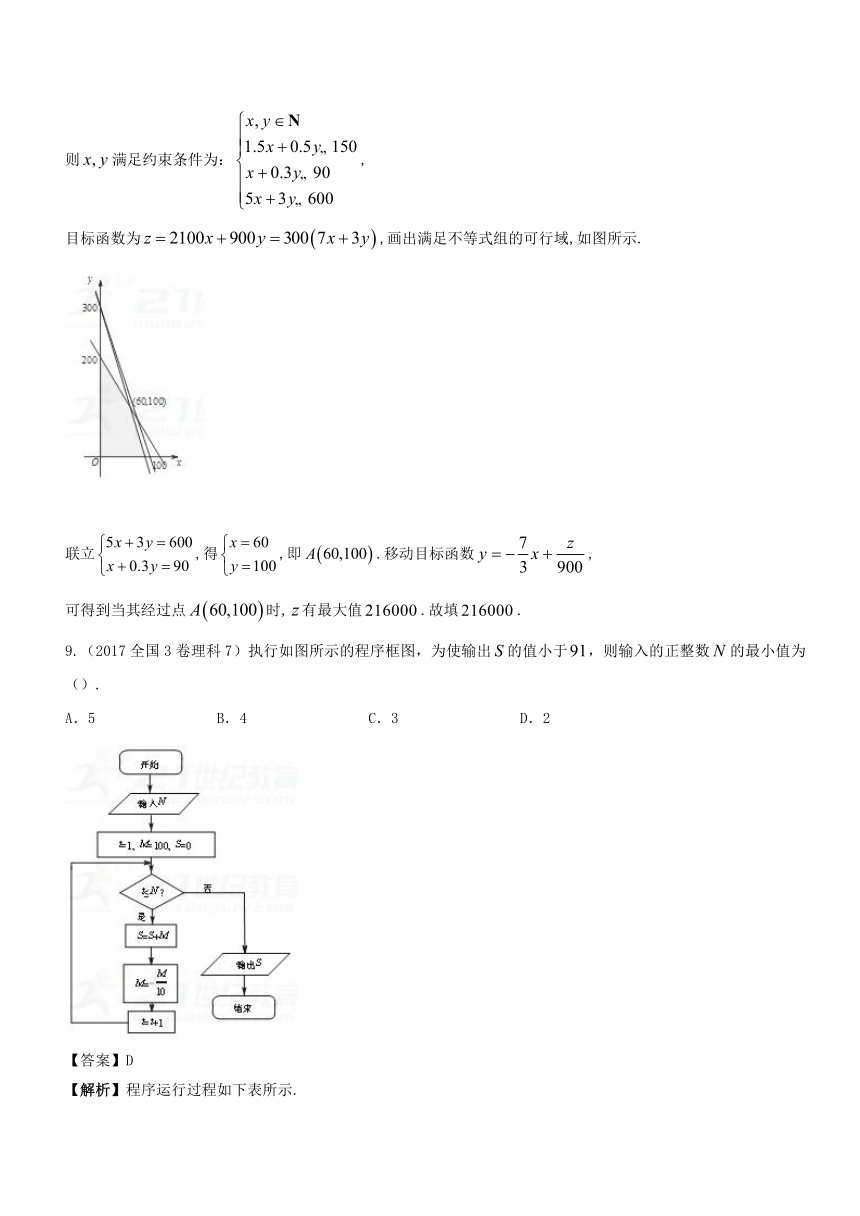
8.【2016全国卷1理】某高科技企业生产产品和产品需要甲、乙两种新型材料.生产一件产品需要甲材料,乙材料,用个工时;生产一件产品需要甲材料,乙材料,用个工时.生产一件产品的利润为元,生产一件产品的利润为元,该企业现有甲材料,乙材料,则在不超过个工时的条件下,生产产品,产品的利润之和的最大值为 元.
【答案】.
【解析】设生产产品A,B的件数分别为,获得利润为元,
则满足约束条件为:,
目标函数为,画出满足不等式组的可行域,如图所示.
联立,得,即.移动目标函数,
可得到当其经过点时,有最大值.故填.
9.(2017全国3卷理科7)执行如图所示的程序框图,为使输出的值小于,则输入的正整数的最小值为().
A.5 B.4 C.3 D.2
【答案】D
【解析】程序运行过程如下表所示.
初始状态
0
100
1
第1次循环结束
100
2
第2次循环结束
90
1
3
此时,首次满足条件,程序需在时跳出循环,即为满足条件的最小值.故选D.
10.【2016全国卷3文理】执行右图的程序框图,如果输入的,那么输出的( ).
A. B. C. D.
【答案】B
11.【2016全国卷1文理】执行如图所示的程序框图,如果输入的,则输出,的值满足( ).
A. B. C. D.
【答案】C
【解析】将程序框图所执行的程序分步计算如表所示.
步骤
?
第一次
否
第二次
否
第三次
是
故输出,,满足.故选C.
12.【2016全国卷2文理】中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的,,依次输入的为2,2,5,则输出的( ).
A.7 B.12 C.17 D.34
【答案】C
【解析】 第一次运算:;第二次运算:;第三次运算:.故选C.
【热点深度剖析】
1.从近几年的高考试题来看,几何体的三视图是高考的热点,题型多为选择题、填空题,难度中、低档.主要考查根据几何体的三视图确定其体积或表面积,在考查三视图的同时,又考查了学生的空间想象能力及运算与推理能力.从近几年的高考试题来看,高考对三视图的考查主要考查由三视图得出几何体的直观图,求其表面积、体积或由几何体的表面积、体积得出某些量;试题难度逐年有所增加,组合体及非正常状态下放置的棱锥的三视图成为考查的热点.纵观这三年高考,每年必考一题,分值5分,.预测2018年高考仍将以组合体及长方体的切割截的三视图为主要考查点,可能与表面积、体积有关,重点考查学生读图、识图能力以及空间想象能力.
2.关于线性规划的考查,从近几年高考试题来看,试题难度较低,属于中低档试题,一般放在选择题的第5-7题或填空题的前两题.从近几年的高考试题来看,二元一次不等式(组)表示的平面区域(的面积),求目标函数的最值,线性规划的应用问题等是高考的热点,题型既有选择题,也有填空题,难度为中、低档题.主要考查平面区域的画法,目标函数最值的求法,以及在取得最值时参数的取值范围.同时注重考查等价转化、数形结合思想.从近几年高考试题,都没涉及含参数的线性规划问题,故预测2018年高考仍将以目标函数的最值为主,理科可能会出现含参数的线性规划问题或距离模型求最值,高考中理科线性规划试题,一般比文科稍大,线性规划的综合运用是主要考查点,重点考查学生分析问题、解决问题的能力.
3.从这三年的高考试题来看.算法试题文理相同,主要考查算法概念和程序框图,理解算法的基本结构,基本算法语句高考很少涉及.命题主要集中在算法的三种基本逻辑结构的框图表示,程序框图与其它知识结合是新的热点.从近几年的高考试题来看,当型与直到型循环结构、条件结构是考查的热点,题型以选择题、填空题为主,文理同题,分值5分左右,属容易题,主要考查算法基本结构以及读图、识图、利用框图解决简单算法问题的能力.预测2018年高考,循环结构与条件结构仍是考查的重点,但应同时注意算法的应用.
【重点知识整合】
1.空间几何体的三视图
三视图是观测者从不同位置观察同一个几何体,画出的空间几何体的图形.
他具体包括:
(1)正视图:物体前后方向投影所得到的投影图;它能反映物体的高度和长度;
(2)侧视图:物体左右方向投影所得到的投影图;它能反映物体的高度和宽度;
(3)俯视图:物体上下方向投影所得到的投影图;它能反映物体的长度和宽度.
2.三视图画法规则
高平齐:主视图与左视图的高要保持平齐
长对正:主视图与俯视图的长应对正
宽相等:俯视图与左视图的宽度应相等
3.平面区域的确定方法是“直线定界,特殊点定域”,二元一次不等式组所表示的平面区域是各个不等式所表示的半平面的交集.确定平面区域中单个变量的范围、整点个数等,只需把区域画出来,结合图形通过计算解决.
4.线性目标函数中的z不是直线在y轴上的截距,把目标函数化为可知是直线在y轴上的截距,要根据b的符号确定目标函数在什么情况下取得最大值、什么情况下取得最小值.
5.线性规划中常见目标函数的转化公式:
(1)截距型:与直线的截距相关联.若b>0,当的最值情况和z的一致;若b<0,当的最值情况和z的相反;
(2)斜率型:
(3)点点距离型:表示到两点距离的平方;
(4)点线距离型:表示到直线的距离的倍.
6.算法的顺序结构:顺序结构是由若干个依次执行的处理步骤组成的,这是任何一个算法都离不开的基本结构.顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连接起来,按顺序执行算法步骤.
7.算法的条件结构: (1)利用条件分支结构解决算法问题时,要引入判断框,要根据题目的要求引入一个或多个判断框,而判断框内的条件不同,对应的下一图框中的内容和操作要相应地进行变化,故要逐个分析判断框内的条件.
(2)解决分段函数的求值问题,一般采用条件结构.
8.利用循环结构表示算法:
(1)先确定是利用当型循环结构,还是直到型循环结构;
(2)选择准确的表示累计的变量;
(3)注意在哪一步开始循环.
9.两种循环结构的特征:
名 称
特 征
直到型循环结构
在执行了一次循环体后,对条件进行判断,如果条件不满足,就继续执行循环体,直到条件满足时终止循环.
当型循环结构
在每次执行循环体前,对条件进行判断,当条件满足时,执行循环体,否则终止循环.
【应试技巧点拨】
1.解决三视图问题的技巧:空间几何体的数量关系也体现在三视图中,正视图和侧视图的“高平齐”,正视图和俯视图的“长对正”,侧视图和俯视图的“宽相等”.也就是说正视图、侧视图的高就是空间几何体的高,正视图、俯视图中的长就是空间几何体的最大长度,侧视图、俯视图中的宽就是空间几何体的最大宽度.在绘制三视图时,分界线和可见轮廓线都用实线画出,被遮挡的部分的轮廓线用虚线表示出来,即“眼见为实、不见为虚”.在三视图的判断与识别中要特别注意其中的“虚线”.
2.要切实弄清常见几何体(圆柱、圆锥、圆台、棱柱、棱锥、棱台、球)的三视图的特征,熟练掌握三视图的投影方向及正视图原理,才能迅速破解三视图问题,由三视图画出其直观图.
3.解答三视图题目时:
(1)可以从熟知的某一视图出发,想象出直观图,再验证其他视图是否正确;
(2)视图中标注的长度在直观图中代表什么,要分辨清楚;
(3)视图之间的数量关系:正俯长对正,正侧高平齐,侧俯宽相等.
4.从能力上来看,三视图着重考查空间想象能力,即空间形体的观察分析和抽象的能力,要求是“四会”:①会画图——根据题设条件画出适合题意的图形或画出自己想作的辅助线(面),作出的图形要直观、虚实分明;②会识图——根据题目给出的图形,想象出立体的形状和有关线面的位置关系;③会析图——对图形进行必要的分解、组合;④会用图——对图形或其某部分进行平移、翻折、旋转、展开或实行割补术;考查逻辑思维能力、运算能力和探索能力.
5.二元一次不等式组表示平面区域的画法:
(1)把二元一次不等式改写成或的形式,前者表示直线的上方区域,后者表示直线的下方区域;
(2)用特殊点判断.判断(或)所表示的平面区域时,只要在直线的一侧任意取一点,将它的的坐标代入不等式,如果该点的坐标满足不等式,不等式就表示该点所在一侧的平面区域;如果不满足不等式,就表示这个点所在区域的另一侧平面区域.特殊的,当时,常把原点作为特殊点.无等号时用虚线表示不包含直线,有等号时用实线表示包含直线;
(3)设点,,若与同号,则P,Q在直线的同侧,异号则在直线的异侧.
6. 线性规划中的分类讨论思想
随着对线性规划的考查逐年的加深,数学思想也开始渗透其中,此类试题给人耳目一新的感觉.其中分类讨论思想先拔头筹.主要类型有:可行域中含有参数引起的讨论和目标函数中含有参数引起的讨论.解法思路关键在于分类标准的得到.
7.应用线性规划解决简单的实际问题
在线性规划的实际问题中把实际问题提炼成数学问题,根据实际问题中的已知条件,找出约束条件和目标函数,然后利用图解法求出最优解.若实际问题要求的最优解是整数解,而我们利用图解法得到的解为非整数解,应作适当的调整,其方法应以目标函数的直线的距离为依据,在直线的附近寻求与此直线距离最近的整点.
8. 线性规划和其它知识交汇点
与线性规划相关的知识非常丰富,如与不等式、函数、函数最值等.所以这些为命题者提供了丰富的素材,与线性规划相关的新颖试题也就层出不穷.此类题目着重考查划归思想和数形结合思想,掌握线性规划问题的“画---移---求---答”四部曲,理解线性规划解题程序的实质是解题的关键.
9.含参变量的线性规划问题是近年来高考命题的热点,由于参数的引入,提高了思维的技巧,增加了解题的难度.参变量的设置形式通常有如下两种:
(1)条件不等式组中含有参变量,由于不能明确可行域的形状,因此增加了解题时画图分析的难度,求解这类问题时要有全局观念,结合目标函数逆向分析题意,整体把握解题的方向;
(2)目标函数中设置参变量,旨在增加探索问题的动态性和开放性.从目标函数的结论入手,对图形的动态分析,对变化过程中的相关量的准确定位,是求解这类问题的主要思维方法.
二元一次不等式组所表示的平面区域,包括平面区域的形状判断、面积以及与平面区域有关的最值问题,简单的线性规划模型在解决实际问题中的应用.
10. 识别程序框图运行和完善程序框图的步骤
识别运行程序框图和完善程序框图是高考的热点.解答这一类问题,第一,要明确程序框图的顺序结构、条件结构和循环结构;第二,要识别运行程序框图,理解框图所解决的实际问题;第三,按照题目的要求完成解答.对程序框图的考查常与数列和函数等知识相结合,进一步强化框图问题的实际背景.
11.解决程序框图问题要注意几个常用变量:
(1)计数变量:用来记录某个事件发生的次数,如.
(2)累加变量:用来计算数据之和,如.
(3)累乘变量:用来计算数据之积,如.
12. 程序框图问题的解法
(1)解答程序框图的相关问题,首先要认清程序框图中每个“框”的含义,然后按程序框图运行的箭头一步一步向前“走”,搞清每走一步产生的结论.
(2)要特别注意在哪一步结束循环,解答循环结构的程序框图,最好的方法是执行完整每一次循环,防止执行程序不彻底,造成错误.
13.判断条件的注意事项
解决此类问题应该注意以下三个方面:一是搞清判断框内的条件由计数变量还是累加变量来表示;二是要注意判断框内的不等式是否带有等号,这直接决定循环次数的多少;三是要准确利用程序框图的赋值语句与两个变量之间的关系,把握程序框图的整体功能,这样可以直接求解结果,减少运算的次数.
14.画程序框图的规则如下:
(1)一个完整的程序框图必须有起止框,用来表示程序的开始和结束.
(2)使用标准的图形符号表示操作,带箭头的流程线表示算法步骤的先后顺序,框图一般按从上到下、从左到右的方向画
(3)算法中间要处理数据或计算,可分别写在不同的处理框中.
(4)如果一个流程由于纸面等原因需要分开画.要在断开处画上连结点,并标出连结的号码.如图一.实际上它们是同一点,只是化不才分开画.用连结点可避免流程线的交叉或过长,使流程图清晰.
(5)注释框不是流程图必需的部分,只是为了提示用户一部分框图的作用以及对某些框图的操作结果进行说明.它帮助阅读流程图的用户更好的理解流程图的来龙去脉.
(6)在图形符号内用于描述的语言要非常简练清楚
6.解决循环结构框图问题,首先要找出控制循环的变量其初值、步长、终值(或控制循环的条件),然后看循环体,循环次数比较少时,可依次列出即可获解,循环次数较多时可先循环几次,找出规律,要特别注意最后输出的是什么,不要出现多一次或少一次循环的错误.
15.在循环结构中,填判断框中的条件是常见命题方式,此条件应依据输出结果来确定,解答时,一般先循环2至3次,发现规律,找出什么时候结束循环,也就找到了循环条件,要特别注意条件“不等式”中是否包括等号.
【考场经验分享】
1.三视图在近几年课改区的高考题都有体现,多面体画图、分析图,用自己的语言描述图,提高借助图形分析问题的能力,培养空间观念,注重三视图与直观图的相互转化及等积转化的思想.因此,三视图的内容应重点训练.与几何体的侧面积和体积有关的计算问题,根据基本概念和公式来计算,要重视方程的思想和割补法、等积转换法的运用.
2.对于简单几何体的组合体的三视图,首先要确定正视,侧视,俯视的方向,其次要注意组合体有哪些几何体组成,弄清它们的组成方式,特别应注意它们的交线的位置.解题时一定耐心加细心,观察准确线与线的位置关系,区分好实线与虚线的不同.此类题目如只是单纯考查三视图,一般难度较低,需保证得全分;若与体积,表面积或组合体相结合,有时难度较大,需要较强的空间想象能力和准确的画图能力,此时若空间想象能力不够,不要花费过多的时间.
3.解线性规划问题的思维精髓是“数形结合”,其关键步骤是在图上完成的,所以作图应尽可能精确,图上操作尽可能规范,假如图上的最优点并不明显易变时,不妨将几个有可能是最优点的坐标都求出来,然后逐一检验,从而得正确解.
4.在通过求直线的截距的最值间接求出的最值式时,要注意:当时,截距取最大值时,也取最大值;截距取最小值时,也取最小值;当时,截距取最大值时,取最小值;截距取最小值时,取最大值.
5.平面区域的确定方法是“直线定界、特殊点定域”,二元一次不等式组所表示的平面区域是各个不等式所表示的半平面的交集.线性目标函数中的不是直线在轴上的截距,把目标函数化为可知是直线在轴上的截距,要根据的符号确定目标函数在什么情况下取得最大值、什么情况下取得最小值.
6.线性规划的实质是把代数问题几何化,即数形结合的思想.
需要注意的是:一,准确无误地作出可行域;二,画目标函数所对应的直线时,要注意与约束条件中的直线的斜率进行比较,避免出错;三,一般情况下,目标函数的最大或最小值会在可行域的端点或边界上取得.
本热点出现的位置一般在试卷的选择题的前5道中的一道,或者填空题的前2道中的一道,试题难度中低档,应该是同学们得全分的题目.但是解题时稍微不慎就容易出现错误,下面总结常见的错误:
7.条件结构中的条件要准确,不能含混不清,要清楚在什么情况下需要作怎样的判断,用什么条件来区分.
8.循环结构中要注意循环控制条件的把握,不要出现多一次循环和少一次循环的错误.
9.要准确掌握各语句的形式、特点.特别是条件语句、循环语句中条件的把握.
【名题精选练兵篇】
1.【2018衡水金卷】已知某几何体的三视图如图所示,则该几何体的体积为( )
A. B. C. D.
【答案】A
【解析】该几何体的直观图如图所示,其左侧部分是一个棱柱去掉一个棱柱组成的,
右侧部分是圆柱组成的,该几何体的体积:
.本题选择A选项.
2.【江西省2018届高三教学质量监测】若一个空间几何体的三视图如图所示,且已知该几何体的体积为,则其表面积为( )
A. B. C. D.
【答案】A
【解析】该几何体是半个圆锥, , ,母线长为,
所以其表面积为 ,故选A
3.【安徽省江淮十校2018届高三第三次(4月)联考】《九章算术》是我国古代内容极为丰富的数学名著,书中提出如下问题:“今有刍童,下广两丈,袤三丈,上广三丈,袤四丈,高三丈,问积几何?”翻译成现代文是“今有上下底面皆为长方形的草垛,下底(指面积较小的长方形)宽丈,长丈;上底(指面积较大的长方形)宽丈,长丈;高丈.问它的体积是多少?”现将该几何体的三视图给出如图所示,则该几何体的体积为( )立方丈.
A. B. C. D.
【答案】A
4.【东北三省三校2018届高三第二次模拟】如图所示,一个三棱锥的的三视图是三个直角三角形,则该三棱锥的体积为( )
A. 3 B. 4 C. 6 D. 8
【答案】B
【解析】如图所示,在长宽高分别为的长方体中,三棱锥对应几何体的三视图即题中的三视图,据此可得该几何体的体积:
,本题选择B选项.
5.【新疆2018届高三第二次模拟】已知实数, 满足,则使不等式恒成立的实数的取值集合是( )
A. B. C. D.
【答案】B
6.【2018年陕西省高三教学质量检测】在由不等式组所确定的三角形区域内随机取一点,则该点到此三角形的三个顶点的距离均不小于1的概率是( )
A. B. C. D.
【答案】D
【解析】画出关于的不等式组所构成的三角形区域,如图所示. 的面积为 离三个顶点距离都不大于1的地方的面积为
∴其恰在离三个顶点距离都不小于1的地方的概率为
故选C.
7.【湖南省张家界市2018届高三第三次模拟】已知变量, 满足,若方程有解,则实数的最小值为( )
A. B. C. D.
【答案】B
【解析】由题意,可作出约束条件的区域图,如图所示,由方程,得,由此问题可转化为求区域图内的点到定点的距离最小时实数的值,结合图形,点到直线的距离为所求,则有,解得.故选B.
8.【山西省榆社中学2018届高三诊断性模拟】设满足约束条件,则的取值范围为( )
A. B. C. D.
【答案】A
【解析】由题意,可作出约束条件的可行域,如图所示,在可行域内,当时, 取得最小值;不妨设的最大值为,则有或,即或,结合图形,当直线过点时, 取得最大值为,所以的取值范围为.故正确答案为A.
9.【湖南省张家界市2018届高三第三次模拟】执行如图所示的程序框图,则输出的( )
A. B. C. 4 D. 5
【答案】D
【解析】由题意,执行程序,由正确,则, ;
由正确,则, ;
由正确,则, ;
由正确,则, ;……
由此可以发现的值为,其值规律为以3为周期,由,所以,当错误,则输出的值为5,故选D.
10.【安徽省宣城市2018届高三第二次调研】执行如图所示的程序框图,如果输入的、均为3,则输出的等于( )
A. B. C. D.
【答案】C
【解析】执行循环得:
,结束循环,输出等于,选C.
11.【海南省2018届高三第二次联合考试】执行如图所示的程序框图,则输出的( )
A. 17 B. 33 C. 65 D. 129
【答案】C
【解析】执行程序框图得: ; ,
结束循环输出.故选C.
12.【2017届广西玉林市、贵港市高三毕业班质量检测】《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )
A. 2 B. 4 C. D.
【答案】D
【解析】由三视图知,该几何体是底面为斜边边长为的等腰直角三角形,高为的直三棱柱,所以该几何体的表面积为,故选D.
13.【2017届福建省泉州市高三3月质量检测】某几何体的三视图如图所示,则该几何体的侧视图中的虚线部分是 ( )
A. 圆弧 B. 抛物线的一部分 C. 椭圆的一部分 D. 双曲线的一部分
【答案】D
【解析】由已知中的三视图可得,侧视图中的虚线部分是由平行与旋转轴的平面截圆锥所得,故侧视图中的虚线部分是双曲线的一部分,故选:D.
14.【2017届福建省莆田市高三下学期质量检查】如图,网格纸上小正方形的边长为,粗实线画出的是某几何体的三视图,若该几何体的顶点都在球的球面上,则球的表面积为( )
A. B. C. D.
【答案】A
【解析】
该几何体可看成是放在长方体中一个三棱锥,如上图,则其外接球心 为长方体的体对角线,则.故选B.
15.【2017届湖南省长沙市高三下学期统一模拟】若,则的最大值与最小值之和是( )
A. 0 B. -2 C. 2 D. 6
【答案】C
【解析】由条件可知 ,求的最大值和最小值的和,如下图,画出可行域, 表示斜率为的一组平行线,当直线过点和时函数取得最大值和最小值, , ,代入目标函数, , ,所以最大值和最小值的和为 ,故选C.
16.【湖北省六校联合体2017届高三4月联考】若变量满足约束条件,且的最大值和最小值分别为和,则( )
A. -2 B. -1 C. 0 D. 1
【答案】C
【解析】
作出不等式组对应的平面区域如图:由,得,平移直线,由图象可知当直线经过点,直线的截距最小,此时最小,由?解得?即,此时,此时,平移直线,由图象可知当直线经过点直线的截距最大,此时最大,由?解得?即,此时,即,则,故选C.
17.【江西省2017届高三4月新课程教学质量监测】不等式组表示的平面区域的面积是( )
A. 1 B. 2 C. 3 D. 4
【答案】A
【解析】
作出不等式组表示的区域是两直角边分别为的直角三角形,面积,故选A.
18.【北京市海淀区2017届高三3月适应性考试】当时,执行如图所示的程序框图,输出的值为( )
A. 6 B. 8 C. 14 D. 30
【答案】D
【解析】第一次循环, ,第二次循环, ,第三次循环, ,第四次循环, , 结束循环,输出,故选D.
19.【2017河北唐山市高三第一次模拟】一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的,则输出的结果()
A. 4 B. C. D.
【答案】C
【解析】 .满足 ,第一次循环: ;满足 ,第二次循环: ;满足,结束循环.故选C.
20.【江西省红色七校2017届高三下学期第二次联考】右边程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示除以的余数),若输入的,分别为485,135,则输出的=( )
A. 0 B. 5 C. 25 D. 45
【答案】B
【名师原创测试篇】
1. 如图在棱长为1的正方体网格中,粗线画出的是某几何体的三视图,则该几何体的体积为 ( ).
A.117 B.111 C.99 D. 75
【答案】D
【解析】该几何体为棱长为6的正方体被一平面截得的一部分,即直观图中的ABCDEFGH,其体积等于五棱锥A-CDFGH,三棱锥C-ABH,三棱锥D-AEF的体积之和,所以该几何体的体积+ +=63+6+6=75,故选D.
2. 某几何体的三视图如图所示,则该几何体的体积为 ( )
A. B. C. D.
【答案】A.
【解析】如下图所示,该几何体的直观图为四棱柱截去三棱锥和三棱锥.由已知底面为直角梯形,底面为的中点,所以该几何体的体积,故选A.
3.已知不等式组表示的平面区域,则的最大值 .
【答案】
【解析】依题意不等式组所表示的平面区域如图所示:由,表示的是可行域到点连线的斜率的最大值,由于,故过的斜率最大,且为,故.
4.已知不等式组所表示的平面区域为,若直线与平面区域有公共点,则的取值范围为是
A. B. C. D.
【答案】C
【解析】不等式组表示的平面区域如图,表示的过定点的直线,,从向转动的过程中,斜率越来越大,转过轴,斜率从逐渐增大到,斜率的取值范围是
,故答案为C.
5.如图所示程序框图中,如果输入三个实数a、b、c,要求输出这三个数中
最小的数,那么在空白的判断框中,应该填入下面四个选项中的( )
A.x【答案】B
6. 如图,这是一个把k进数a(共有n位)化为十进制数b的程序框图,执行该程序框图,若输人的k,a,n分别为2,110011,6,则输出的b= .
【答案】51
【解析】 依程序框图得.
热点二 客观题中的三视图、线性规划、框图
【名师精讲指南篇】
【高考真题再现】
1.(2017全国1卷理科7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为().
A. B. C. D.
【答案】B
【解析】由三视图可画出立体图,如图所示,该多面体只有两个相同的梯形的面,
,.故选B.
2.(2107全国2卷理科4)如图所示,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为().
A. B. C. D.
【答案】B
【解析】该几何体可视为一个完整的圆柱减去一个高为6的圆柱的一半,如图所示.
.故选B.
3.【2016全国卷2】右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( ).
A.20π B.24π C.28π D.32π
【答案】C
4.【2016全国卷1】如图所示,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是,则它的表面积是( ).
A. B. C. D.
【答案】A
【解析】由几何体的三视图可知,其是一个球被切掉左上角的后的几何体.表面积是的球面面积和三个扇形面积之和.由,得,所以.因此.故选A.
5.(2017全国1理14)设x,y满足约束条件,则的最小值为.
【答案】-5.
6.(2017全国2理5)设,满足约束条件,则的最小值是().
A. B. C. D.
【答案】A
【解析】目标区域如图所示,当直线过点时,所求取到最小值为.故选A.
7.【2016全国卷3文】设,满足约束条件,则的最小值为______.
【答案】
【解析】可行域为及其内部,其中,直线过点时取最小值.
【答案】
【解析】 可行域如图所示.当直线经过时,取最大值为.
8.【2016全国卷1理】某高科技企业生产产品和产品需要甲、乙两种新型材料.生产一件产品需要甲材料,乙材料,用个工时;生产一件产品需要甲材料,乙材料,用个工时.生产一件产品的利润为元,生产一件产品的利润为元,该企业现有甲材料,乙材料,则在不超过个工时的条件下,生产产品,产品的利润之和的最大值为 元.
【答案】.
【解析】设生产产品A,B的件数分别为,获得利润为元,
则满足约束条件为:,
目标函数为,画出满足不等式组的可行域,如图所示.
联立,得,即.移动目标函数,
可得到当其经过点时,有最大值.故填.
9.(2017全国3卷理科7)执行如图所示的程序框图,为使输出的值小于,则输入的正整数的最小值为().
A.5 B.4 C.3 D.2
【答案】D
【解析】程序运行过程如下表所示.
初始状态
0
100
1
第1次循环结束
100
2
第2次循环结束
90
1
3
此时,首次满足条件,程序需在时跳出循环,即为满足条件的最小值.故选D.
10.【2016全国卷3文理】执行右图的程序框图,如果输入的,那么输出的( ).
A. B. C. D.
【答案】B
11.【2016全国卷1文理】执行如图所示的程序框图,如果输入的,则输出,的值满足( ).
A. B. C. D.
【答案】C
【解析】将程序框图所执行的程序分步计算如表所示.
步骤
?
第一次
否
第二次
否
第三次
是
故输出,,满足.故选C.
12.【2016全国卷2文理】中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的,,依次输入的为2,2,5,则输出的( ).
A.7 B.12 C.17 D.34
【答案】C
【解析】 第一次运算:;第二次运算:;第三次运算:.故选C.
【热点深度剖析】
1.从近几年的高考试题来看,几何体的三视图是高考的热点,题型多为选择题、填空题,难度中、低档.主要考查根据几何体的三视图确定其体积或表面积,在考查三视图的同时,又考查了学生的空间想象能力及运算与推理能力.从近几年的高考试题来看,高考对三视图的考查主要考查由三视图得出几何体的直观图,求其表面积、体积或由几何体的表面积、体积得出某些量;试题难度逐年有所增加,组合体及非正常状态下放置的棱锥的三视图成为考查的热点.纵观这三年高考,每年必考一题,分值5分,.预测2018年高考仍将以组合体及长方体的切割截的三视图为主要考查点,可能与表面积、体积有关,重点考查学生读图、识图能力以及空间想象能力.
2.关于线性规划的考查,从近几年高考试题来看,试题难度较低,属于中低档试题,一般放在选择题的第5-7题或填空题的前两题.从近几年的高考试题来看,二元一次不等式(组)表示的平面区域(的面积),求目标函数的最值,线性规划的应用问题等是高考的热点,题型既有选择题,也有填空题,难度为中、低档题.主要考查平面区域的画法,目标函数最值的求法,以及在取得最值时参数的取值范围.同时注重考查等价转化、数形结合思想.从近几年高考试题,都没涉及含参数的线性规划问题,故预测2018年高考仍将以目标函数的最值为主,理科可能会出现含参数的线性规划问题或距离模型求最值,高考中理科线性规划试题,一般比文科稍大,线性规划的综合运用是主要考查点,重点考查学生分析问题、解决问题的能力.
3.从这三年的高考试题来看.算法试题文理相同,主要考查算法概念和程序框图,理解算法的基本结构,基本算法语句高考很少涉及.命题主要集中在算法的三种基本逻辑结构的框图表示,程序框图与其它知识结合是新的热点.从近几年的高考试题来看,当型与直到型循环结构、条件结构是考查的热点,题型以选择题、填空题为主,文理同题,分值5分左右,属容易题,主要考查算法基本结构以及读图、识图、利用框图解决简单算法问题的能力.预测2018年高考,循环结构与条件结构仍是考查的重点,但应同时注意算法的应用.
【重点知识整合】
1.空间几何体的三视图
三视图是观测者从不同位置观察同一个几何体,画出的空间几何体的图形.
他具体包括:
(1)正视图:物体前后方向投影所得到的投影图;它能反映物体的高度和长度;
(2)侧视图:物体左右方向投影所得到的投影图;它能反映物体的高度和宽度;
(3)俯视图:物体上下方向投影所得到的投影图;它能反映物体的长度和宽度.
2.三视图画法规则
高平齐:主视图与左视图的高要保持平齐
长对正:主视图与俯视图的长应对正
宽相等:俯视图与左视图的宽度应相等
3.平面区域的确定方法是“直线定界,特殊点定域”,二元一次不等式组所表示的平面区域是各个不等式所表示的半平面的交集.确定平面区域中单个变量的范围、整点个数等,只需把区域画出来,结合图形通过计算解决.
4.线性目标函数中的z不是直线在y轴上的截距,把目标函数化为可知是直线在y轴上的截距,要根据b的符号确定目标函数在什么情况下取得最大值、什么情况下取得最小值.
5.线性规划中常见目标函数的转化公式:
(1)截距型:与直线的截距相关联.若b>0,当的最值情况和z的一致;若b<0,当的最值情况和z的相反;
(2)斜率型:
(3)点点距离型:表示到两点距离的平方;
(4)点线距离型:表示到直线的距离的倍.
6.算法的顺序结构:顺序结构是由若干个依次执行的处理步骤组成的,这是任何一个算法都离不开的基本结构.顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连接起来,按顺序执行算法步骤.
7.算法的条件结构: (1)利用条件分支结构解决算法问题时,要引入判断框,要根据题目的要求引入一个或多个判断框,而判断框内的条件不同,对应的下一图框中的内容和操作要相应地进行变化,故要逐个分析判断框内的条件.
(2)解决分段函数的求值问题,一般采用条件结构.
8.利用循环结构表示算法:
(1)先确定是利用当型循环结构,还是直到型循环结构;
(2)选择准确的表示累计的变量;
(3)注意在哪一步开始循环.
9.两种循环结构的特征:
名 称
特 征
直到型循环结构
在执行了一次循环体后,对条件进行判断,如果条件不满足,就继续执行循环体,直到条件满足时终止循环.
当型循环结构
在每次执行循环体前,对条件进行判断,当条件满足时,执行循环体,否则终止循环.
【应试技巧点拨】
1.解决三视图问题的技巧:空间几何体的数量关系也体现在三视图中,正视图和侧视图的“高平齐”,正视图和俯视图的“长对正”,侧视图和俯视图的“宽相等”.也就是说正视图、侧视图的高就是空间几何体的高,正视图、俯视图中的长就是空间几何体的最大长度,侧视图、俯视图中的宽就是空间几何体的最大宽度.在绘制三视图时,分界线和可见轮廓线都用实线画出,被遮挡的部分的轮廓线用虚线表示出来,即“眼见为实、不见为虚”.在三视图的判断与识别中要特别注意其中的“虚线”.
2.要切实弄清常见几何体(圆柱、圆锥、圆台、棱柱、棱锥、棱台、球)的三视图的特征,熟练掌握三视图的投影方向及正视图原理,才能迅速破解三视图问题,由三视图画出其直观图.
3.解答三视图题目时:
(1)可以从熟知的某一视图出发,想象出直观图,再验证其他视图是否正确;
(2)视图中标注的长度在直观图中代表什么,要分辨清楚;
(3)视图之间的数量关系:正俯长对正,正侧高平齐,侧俯宽相等.
4.从能力上来看,三视图着重考查空间想象能力,即空间形体的观察分析和抽象的能力,要求是“四会”:①会画图——根据题设条件画出适合题意的图形或画出自己想作的辅助线(面),作出的图形要直观、虚实分明;②会识图——根据题目给出的图形,想象出立体的形状和有关线面的位置关系;③会析图——对图形进行必要的分解、组合;④会用图——对图形或其某部分进行平移、翻折、旋转、展开或实行割补术;考查逻辑思维能力、运算能力和探索能力.
5.二元一次不等式组表示平面区域的画法:
(1)把二元一次不等式改写成或的形式,前者表示直线的上方区域,后者表示直线的下方区域;
(2)用特殊点判断.判断(或)所表示的平面区域时,只要在直线的一侧任意取一点,将它的的坐标代入不等式,如果该点的坐标满足不等式,不等式就表示该点所在一侧的平面区域;如果不满足不等式,就表示这个点所在区域的另一侧平面区域.特殊的,当时,常把原点作为特殊点.无等号时用虚线表示不包含直线,有等号时用实线表示包含直线;
(3)设点,,若与同号,则P,Q在直线的同侧,异号则在直线的异侧.
6. 线性规划中的分类讨论思想
随着对线性规划的考查逐年的加深,数学思想也开始渗透其中,此类试题给人耳目一新的感觉.其中分类讨论思想先拔头筹.主要类型有:可行域中含有参数引起的讨论和目标函数中含有参数引起的讨论.解法思路关键在于分类标准的得到.
7.应用线性规划解决简单的实际问题
在线性规划的实际问题中把实际问题提炼成数学问题,根据实际问题中的已知条件,找出约束条件和目标函数,然后利用图解法求出最优解.若实际问题要求的最优解是整数解,而我们利用图解法得到的解为非整数解,应作适当的调整,其方法应以目标函数的直线的距离为依据,在直线的附近寻求与此直线距离最近的整点.
8. 线性规划和其它知识交汇点
与线性规划相关的知识非常丰富,如与不等式、函数、函数最值等.所以这些为命题者提供了丰富的素材,与线性规划相关的新颖试题也就层出不穷.此类题目着重考查划归思想和数形结合思想,掌握线性规划问题的“画---移---求---答”四部曲,理解线性规划解题程序的实质是解题的关键.
9.含参变量的线性规划问题是近年来高考命题的热点,由于参数的引入,提高了思维的技巧,增加了解题的难度.参变量的设置形式通常有如下两种:
(1)条件不等式组中含有参变量,由于不能明确可行域的形状,因此增加了解题时画图分析的难度,求解这类问题时要有全局观念,结合目标函数逆向分析题意,整体把握解题的方向;
(2)目标函数中设置参变量,旨在增加探索问题的动态性和开放性.从目标函数的结论入手,对图形的动态分析,对变化过程中的相关量的准确定位,是求解这类问题的主要思维方法.
二元一次不等式组所表示的平面区域,包括平面区域的形状判断、面积以及与平面区域有关的最值问题,简单的线性规划模型在解决实际问题中的应用.
10. 识别程序框图运行和完善程序框图的步骤
识别运行程序框图和完善程序框图是高考的热点.解答这一类问题,第一,要明确程序框图的顺序结构、条件结构和循环结构;第二,要识别运行程序框图,理解框图所解决的实际问题;第三,按照题目的要求完成解答.对程序框图的考查常与数列和函数等知识相结合,进一步强化框图问题的实际背景.
11.解决程序框图问题要注意几个常用变量:
(1)计数变量:用来记录某个事件发生的次数,如.
(2)累加变量:用来计算数据之和,如.
(3)累乘变量:用来计算数据之积,如.
12. 程序框图问题的解法
(1)解答程序框图的相关问题,首先要认清程序框图中每个“框”的含义,然后按程序框图运行的箭头一步一步向前“走”,搞清每走一步产生的结论.
(2)要特别注意在哪一步结束循环,解答循环结构的程序框图,最好的方法是执行完整每一次循环,防止执行程序不彻底,造成错误.
13.判断条件的注意事项
解决此类问题应该注意以下三个方面:一是搞清判断框内的条件由计数变量还是累加变量来表示;二是要注意判断框内的不等式是否带有等号,这直接决定循环次数的多少;三是要准确利用程序框图的赋值语句与两个变量之间的关系,把握程序框图的整体功能,这样可以直接求解结果,减少运算的次数.
14.画程序框图的规则如下:
(1)一个完整的程序框图必须有起止框,用来表示程序的开始和结束.
(2)使用标准的图形符号表示操作,带箭头的流程线表示算法步骤的先后顺序,框图一般按从上到下、从左到右的方向画
(3)算法中间要处理数据或计算,可分别写在不同的处理框中.
(4)如果一个流程由于纸面等原因需要分开画.要在断开处画上连结点,并标出连结的号码.如图一.实际上它们是同一点,只是化不才分开画.用连结点可避免流程线的交叉或过长,使流程图清晰.
(5)注释框不是流程图必需的部分,只是为了提示用户一部分框图的作用以及对某些框图的操作结果进行说明.它帮助阅读流程图的用户更好的理解流程图的来龙去脉.
(6)在图形符号内用于描述的语言要非常简练清楚
6.解决循环结构框图问题,首先要找出控制循环的变量其初值、步长、终值(或控制循环的条件),然后看循环体,循环次数比较少时,可依次列出即可获解,循环次数较多时可先循环几次,找出规律,要特别注意最后输出的是什么,不要出现多一次或少一次循环的错误.
15.在循环结构中,填判断框中的条件是常见命题方式,此条件应依据输出结果来确定,解答时,一般先循环2至3次,发现规律,找出什么时候结束循环,也就找到了循环条件,要特别注意条件“不等式”中是否包括等号.
【考场经验分享】
1.三视图在近几年课改区的高考题都有体现,多面体画图、分析图,用自己的语言描述图,提高借助图形分析问题的能力,培养空间观念,注重三视图与直观图的相互转化及等积转化的思想.因此,三视图的内容应重点训练.与几何体的侧面积和体积有关的计算问题,根据基本概念和公式来计算,要重视方程的思想和割补法、等积转换法的运用.
2.对于简单几何体的组合体的三视图,首先要确定正视,侧视,俯视的方向,其次要注意组合体有哪些几何体组成,弄清它们的组成方式,特别应注意它们的交线的位置.解题时一定耐心加细心,观察准确线与线的位置关系,区分好实线与虚线的不同.此类题目如只是单纯考查三视图,一般难度较低,需保证得全分;若与体积,表面积或组合体相结合,有时难度较大,需要较强的空间想象能力和准确的画图能力,此时若空间想象能力不够,不要花费过多的时间.
3.解线性规划问题的思维精髓是“数形结合”,其关键步骤是在图上完成的,所以作图应尽可能精确,图上操作尽可能规范,假如图上的最优点并不明显易变时,不妨将几个有可能是最优点的坐标都求出来,然后逐一检验,从而得正确解.
4.在通过求直线的截距的最值间接求出的最值式时,要注意:当时,截距取最大值时,也取最大值;截距取最小值时,也取最小值;当时,截距取最大值时,取最小值;截距取最小值时,取最大值.
5.平面区域的确定方法是“直线定界、特殊点定域”,二元一次不等式组所表示的平面区域是各个不等式所表示的半平面的交集.线性目标函数中的不是直线在轴上的截距,把目标函数化为可知是直线在轴上的截距,要根据的符号确定目标函数在什么情况下取得最大值、什么情况下取得最小值.
6.线性规划的实质是把代数问题几何化,即数形结合的思想.
需要注意的是:一,准确无误地作出可行域;二,画目标函数所对应的直线时,要注意与约束条件中的直线的斜率进行比较,避免出错;三,一般情况下,目标函数的最大或最小值会在可行域的端点或边界上取得.
本热点出现的位置一般在试卷的选择题的前5道中的一道,或者填空题的前2道中的一道,试题难度中低档,应该是同学们得全分的题目.但是解题时稍微不慎就容易出现错误,下面总结常见的错误:
7.条件结构中的条件要准确,不能含混不清,要清楚在什么情况下需要作怎样的判断,用什么条件来区分.
8.循环结构中要注意循环控制条件的把握,不要出现多一次循环和少一次循环的错误.
9.要准确掌握各语句的形式、特点.特别是条件语句、循环语句中条件的把握.
【名题精选练兵篇】
1.【2018衡水金卷】已知某几何体的三视图如图所示,则该几何体的体积为( )
A. B. C. D.
【答案】A
【解析】该几何体的直观图如图所示,其左侧部分是一个棱柱去掉一个棱柱组成的,
右侧部分是圆柱组成的,该几何体的体积:
.本题选择A选项.
2.【江西省2018届高三教学质量监测】若一个空间几何体的三视图如图所示,且已知该几何体的体积为,则其表面积为( )
A. B. C. D.
【答案】A
【解析】该几何体是半个圆锥, , ,母线长为,
所以其表面积为 ,故选A
3.【安徽省江淮十校2018届高三第三次(4月)联考】《九章算术》是我国古代内容极为丰富的数学名著,书中提出如下问题:“今有刍童,下广两丈,袤三丈,上广三丈,袤四丈,高三丈,问积几何?”翻译成现代文是“今有上下底面皆为长方形的草垛,下底(指面积较小的长方形)宽丈,长丈;上底(指面积较大的长方形)宽丈,长丈;高丈.问它的体积是多少?”现将该几何体的三视图给出如图所示,则该几何体的体积为( )立方丈.
A. B. C. D.
【答案】A
4.【东北三省三校2018届高三第二次模拟】如图所示,一个三棱锥的的三视图是三个直角三角形,则该三棱锥的体积为( )
A. 3 B. 4 C. 6 D. 8
【答案】B
【解析】如图所示,在长宽高分别为的长方体中,三棱锥对应几何体的三视图即题中的三视图,据此可得该几何体的体积:
,本题选择B选项.
5.【新疆2018届高三第二次模拟】已知实数, 满足,则使不等式恒成立的实数的取值集合是( )
A. B. C. D.
【答案】B
6.【2018年陕西省高三教学质量检测】在由不等式组所确定的三角形区域内随机取一点,则该点到此三角形的三个顶点的距离均不小于1的概率是( )
A. B. C. D.
【答案】D
【解析】画出关于的不等式组所构成的三角形区域,如图所示. 的面积为 离三个顶点距离都不大于1的地方的面积为
∴其恰在离三个顶点距离都不小于1的地方的概率为
故选C.
7.【湖南省张家界市2018届高三第三次模拟】已知变量, 满足,若方程有解,则实数的最小值为( )
A. B. C. D.
【答案】B
【解析】由题意,可作出约束条件的区域图,如图所示,由方程,得,由此问题可转化为求区域图内的点到定点的距离最小时实数的值,结合图形,点到直线的距离为所求,则有,解得.故选B.
8.【山西省榆社中学2018届高三诊断性模拟】设满足约束条件,则的取值范围为( )
A. B. C. D.
【答案】A
【解析】由题意,可作出约束条件的可行域,如图所示,在可行域内,当时, 取得最小值;不妨设的最大值为,则有或,即或,结合图形,当直线过点时, 取得最大值为,所以的取值范围为.故正确答案为A.
9.【湖南省张家界市2018届高三第三次模拟】执行如图所示的程序框图,则输出的( )
A. B. C. 4 D. 5
【答案】D
【解析】由题意,执行程序,由正确,则, ;
由正确,则, ;
由正确,则, ;
由正确,则, ;……
由此可以发现的值为,其值规律为以3为周期,由,所以,当错误,则输出的值为5,故选D.
10.【安徽省宣城市2018届高三第二次调研】执行如图所示的程序框图,如果输入的、均为3,则输出的等于( )
A. B. C. D.
【答案】C
【解析】执行循环得:
,结束循环,输出等于,选C.
11.【海南省2018届高三第二次联合考试】执行如图所示的程序框图,则输出的( )
A. 17 B. 33 C. 65 D. 129
【答案】C
【解析】执行程序框图得: ; ,
结束循环输出.故选C.
12.【2017届广西玉林市、贵港市高三毕业班质量检测】《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )
A. 2 B. 4 C. D.
【答案】D
【解析】由三视图知,该几何体是底面为斜边边长为的等腰直角三角形,高为的直三棱柱,所以该几何体的表面积为,故选D.
13.【2017届福建省泉州市高三3月质量检测】某几何体的三视图如图所示,则该几何体的侧视图中的虚线部分是 ( )
A. 圆弧 B. 抛物线的一部分 C. 椭圆的一部分 D. 双曲线的一部分
【答案】D
【解析】由已知中的三视图可得,侧视图中的虚线部分是由平行与旋转轴的平面截圆锥所得,故侧视图中的虚线部分是双曲线的一部分,故选:D.
14.【2017届福建省莆田市高三下学期质量检查】如图,网格纸上小正方形的边长为,粗实线画出的是某几何体的三视图,若该几何体的顶点都在球的球面上,则球的表面积为( )
A. B. C. D.
【答案】A
【解析】
该几何体可看成是放在长方体中一个三棱锥,如上图,则其外接球心 为长方体的体对角线,则.故选B.
15.【2017届湖南省长沙市高三下学期统一模拟】若,则的最大值与最小值之和是( )
A. 0 B. -2 C. 2 D. 6
【答案】C
【解析】由条件可知 ,求的最大值和最小值的和,如下图,画出可行域, 表示斜率为的一组平行线,当直线过点和时函数取得最大值和最小值, , ,代入目标函数, , ,所以最大值和最小值的和为 ,故选C.
16.【湖北省六校联合体2017届高三4月联考】若变量满足约束条件,且的最大值和最小值分别为和,则( )
A. -2 B. -1 C. 0 D. 1
【答案】C
【解析】
作出不等式组对应的平面区域如图:由,得,平移直线,由图象可知当直线经过点,直线的截距最小,此时最小,由?解得?即,此时,此时,平移直线,由图象可知当直线经过点直线的截距最大,此时最大,由?解得?即,此时,即,则,故选C.
17.【江西省2017届高三4月新课程教学质量监测】不等式组表示的平面区域的面积是( )
A. 1 B. 2 C. 3 D. 4
【答案】A
【解析】
作出不等式组表示的区域是两直角边分别为的直角三角形,面积,故选A.
18.【北京市海淀区2017届高三3月适应性考试】当时,执行如图所示的程序框图,输出的值为( )
A. 6 B. 8 C. 14 D. 30
【答案】D
【解析】第一次循环, ,第二次循环, ,第三次循环, ,第四次循环, , 结束循环,输出,故选D.
19.【2017河北唐山市高三第一次模拟】一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的,则输出的结果()
A. 4 B. C. D.
【答案】C
【解析】 .满足 ,第一次循环: ;满足 ,第二次循环: ;满足,结束循环.故选C.
20.【江西省红色七校2017届高三下学期第二次联考】右边程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示除以的余数),若输入的,分别为485,135,则输出的=( )
A. 0 B. 5 C. 25 D. 45
【答案】B
【名师原创测试篇】
1. 如图在棱长为1的正方体网格中,粗线画出的是某几何体的三视图,则该几何体的体积为 ( ).
A.117 B.111 C.99 D. 75
【答案】D
【解析】该几何体为棱长为6的正方体被一平面截得的一部分,即直观图中的ABCDEFGH,其体积等于五棱锥A-CDFGH,三棱锥C-ABH,三棱锥D-AEF的体积之和,所以该几何体的体积+ +=63+6+6=75,故选D.
2. 某几何体的三视图如图所示,则该几何体的体积为 ( )
A. B. C. D.
【答案】A.
【解析】如下图所示,该几何体的直观图为四棱柱截去三棱锥和三棱锥.由已知底面为直角梯形,底面为的中点,所以该几何体的体积,故选A.
3.已知不等式组表示的平面区域,则的最大值 .
【答案】
【解析】依题意不等式组所表示的平面区域如图所示:由,表示的是可行域到点连线的斜率的最大值,由于,故过的斜率最大,且为,故.
4.已知不等式组所表示的平面区域为,若直线与平面区域有公共点,则的取值范围为是
A. B. C. D.
【答案】C
【解析】不等式组表示的平面区域如图,表示的过定点的直线,,从向转动的过程中,斜率越来越大,转过轴,斜率从逐渐增大到,斜率的取值范围是
,故答案为C.
5.如图所示程序框图中,如果输入三个实数a、b、c,要求输出这三个数中
最小的数,那么在空白的判断框中,应该填入下面四个选项中的( )
A.x
6. 如图,这是一个把k进数a(共有n位)化为十进制数b的程序框图,执行该程序框图,若输人的k,a,n分别为2,110011,6,则输出的b= .
【答案】51
【解析】 依程序框图得.
同课章节目录
