2008高考一轮复习课件_第3讲 力的合成与分解[上学期]
文档属性
| 名称 | 2008高考一轮复习课件_第3讲 力的合成与分解[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 591.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2007-08-13 21:23:00 | ||
图片预览





文档简介
课件28张PPT。第3讲 力的合成与分解 力的合成与分解的方法是矢量的合成与分解的基础,体现了等效思维方法.高考对力的合成与分解的考查频繁出现,它通常渗透在平衡问题、运动与力的综合、动量与能量的综合题之中,正交分解法是其中的重要考点.主要题型有计算题与选择题.
本讲复习要求理解合力与分力的关系;掌握力的平行四边形定则;会求两个力的合力;能够根据力的作用效果进行分解并求力;能够用正交分解法求出多个力的合力;能用“图解法”定性分析力的变化情况.
复习时,要求掌握求合力的四种常用的方法(公式法、平行四边形法、三角形法、正交分解法);掌握按效果分解的原则(效果确定方向、法则确定大小);会利用一种特殊类型的力的分解求极值.复习指南第3讲 课前热身 1. 下面关于合力与分力的叙述正确的是 ( )
?A. 一个物体受到几个力的作用,同时也受到这几个力的合力的作用
B. 几个力的合力总是大于它各个分力中最小的力
?C. 一个力分解成两个分力,可以得到无数对大小、方向不同的分力
?D. 合力和它相应的分力可以相互替代CD 2. 四个共点力的大小分别为2 N、3 N、4 N、6 N,它们的合力最大值为 15 N ,它们的合力最小值为 0 . 【解析】 它们的合力最大值Fmax=(2+3+4+6)N=
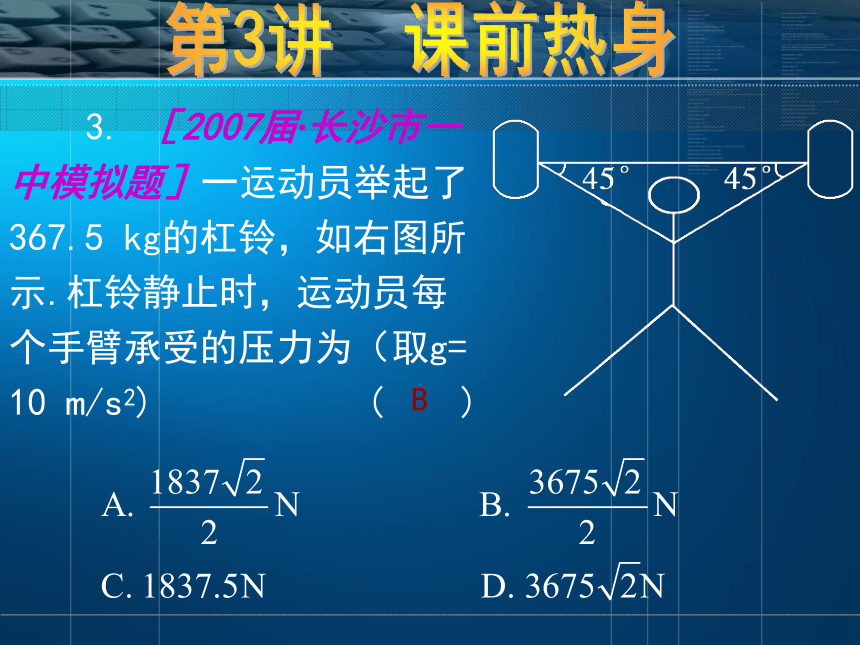
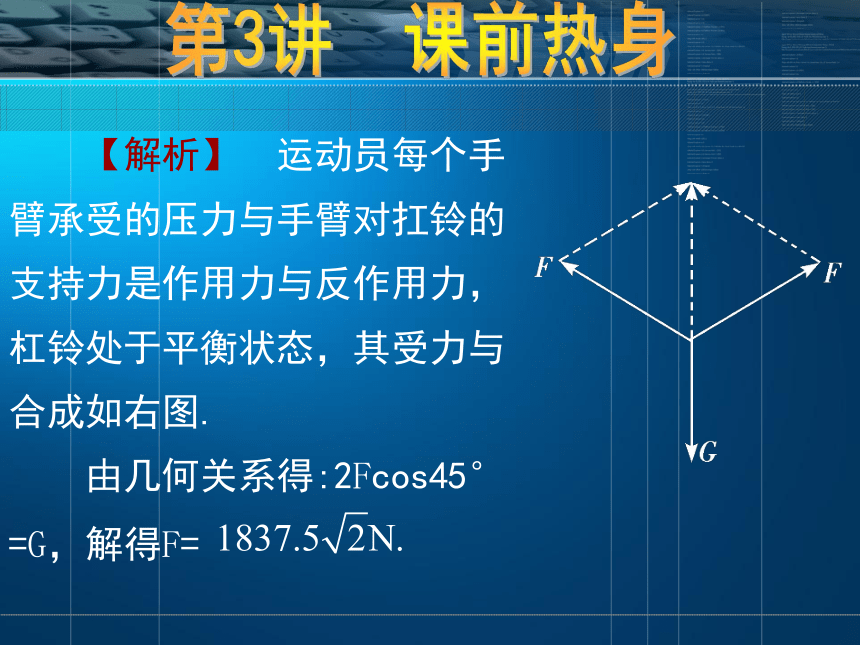
15 N.因为Fm=6N<(2+3+4)N,所以它们的合力最小值为0. 3. [2007届·长沙市一中模拟题]一运动员举起了367.5 kg的杠铃,如右图所示.杠铃静止时,运动员每个手臂承受的压力为(取g=10 m/s2) ( )B第3讲 课前热身 【解析】 运动员每个手臂承受的压力与手臂对扛铃的支持力是作用力与反作用力,杠铃处于平衡状态,其受力与合成如右图.
由几何关系得:2Fcos45°
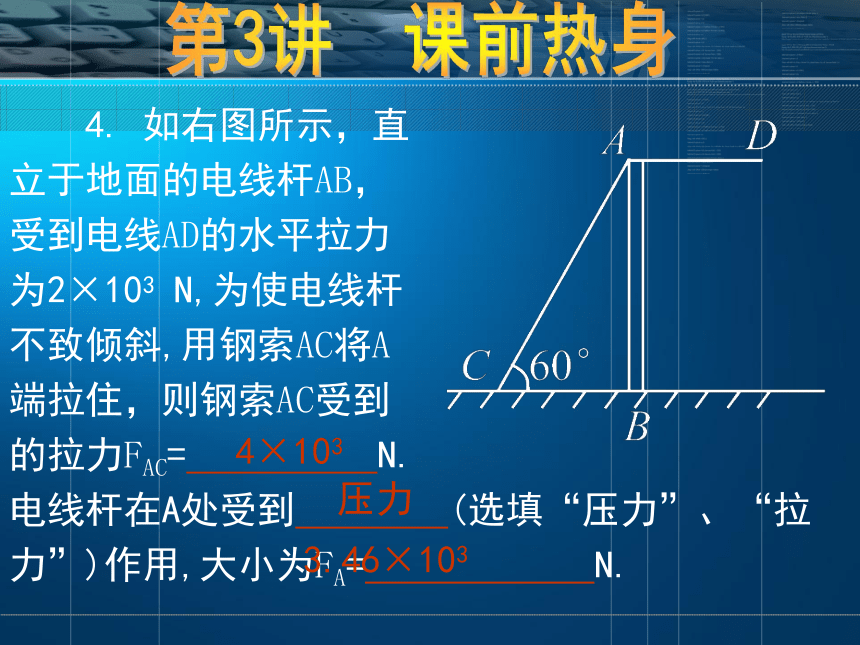
=G,解得F=第3讲 课前热身 4. 如右图所示,直
立于地面的电线杆AB,
受到电线AD的水平拉力
为2×103 N,为使电线杆
不致倾斜,用钢索AC将A
端拉住,则钢索AC受到
的拉力FAC= N.
电线杆在A处受到 (选填“压力”、“拉力”)作用,大小为FA= N.第3讲 课前热身4×103压力3.46×103 【解析】钢索AC的拉
力产生沿水平方向拉杆和
沿竖直方向压杆两种效果,
因此,将其分解如右图所
示.由题意,电线杆不倾
斜有FACcos60°=2×103N,
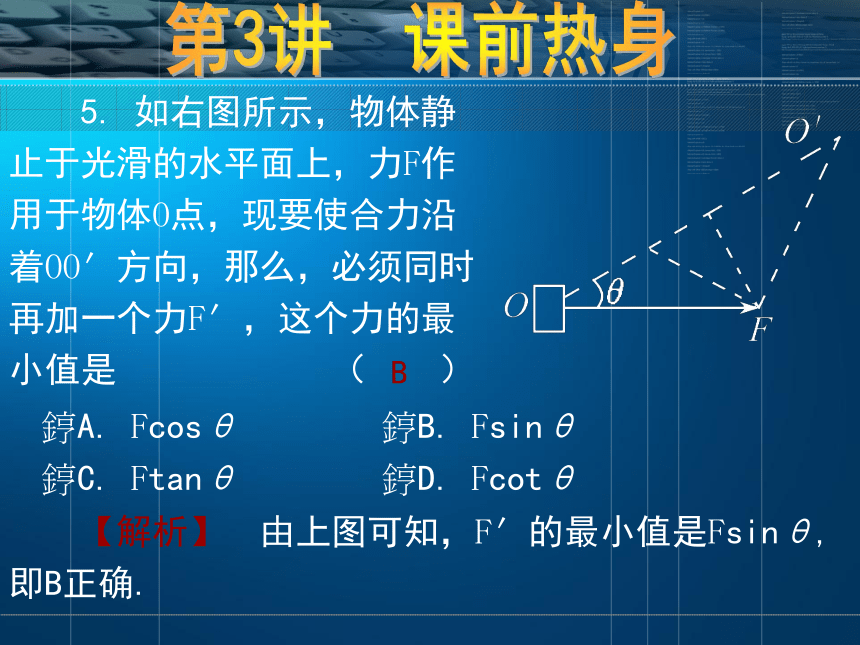
FA=FACsin60°解得FAC=4×103N,FA=3.46×103N.第3讲 课前热身 5. 如右图所示,物体静止于光滑的水平面上,力F作用于物体O点,现要使合力沿着OO′方向,那么,必须同时再加一个力F′,这个力的最小值是 ( )B 【解析】 由上图可知,F′的最小值是Fsinθ,即B正确. ?A. Fcosθ ?B. Fsinθ
?C. Ftanθ ?D. Fcotθ第3讲 课前热身第3讲 考点整合 一、合力与分力的关系
1. 等效关系:合力与它的分力产生的作用效果完全相同.
2. 满足力的平行四边形定则:对角线对应合力、两邻边对应两分力(它还可衍生三角形定则).
3. 可相互替代:在研究力的作用效果时可以相互替代,体现了等效思想.
(1)用合力替代分力,要用到力的合成;
(2)用分力替代合力,要用到力的分解. 二、合力公式及其推论(已知F1、F2及θ)
合力公式:
推 论:第3讲 考点整合 三、力的分解(已知合力求分力的大小与方向)
1. 力的有效分解的原则:由合力产生的实际效果确定分力的方向,由平行四边形定则确定分力的大小.
2. 力的分解的三种类型: (1)已知合力和两个分力的方向,求两个分力的大小.(有唯一解)
(2)已知合力和一个分力的大小与方向,求另一分力的大小和方向.(有唯一解)
(3)已知合力、一个分力F1的大小与另一分力F2的方向,求F1的方向和F2的大小.(当F1=Fsinθ时,有唯一解;当Fsinθ<F1<F时,有两个解; 当F1>F时,分解是唯一的)
3. 力的正交分解法:将已知力按互相垂直的两个方向进行分解的方法.其目的是将不同方向的矢量运算简化为同一直线上的代数运算.第3讲 考点整合第3讲 重点探究探究点一 合力与分力的图示 例1 (1)指出图1-3-7所示每幅图中的合力与分力,并说明它们的关系. (2)如右图所示是力
的平行四边形定则示意
图.若力F1、F2大小不变,
F1的方向可在0°≤θ≤
180°范围内变化,以D为
圆心,以F1的大小AB为半径画半圆.则半圆上任一点与点A的连线表示怎样的物理意义?并结合该图谈谈合力与分力的关系.第3讲 重点探究 【解析】 (1)每幅图中的合力与分力及其关系分别是:
图A:由平行四边形定则可知,力F1、F2的合力为F3.
图B:由三角形定则可知,力F1、F2的合力为F3.
图C:由三角形定则可知,力F1、F3的合力为F2.
图D:由三角形定则可知,力F1、F2、F3的合力为零.
(2)两个不共线的共点力与它们的合力构成三角形,分力和合力的关系实际上就是三角形的一个边和其他两边的关系,题中所讲的半圆上任一点与第3讲 重点探究点A的连线表示F1、F2的合力.根据三角形两边之和应大于第三边.两边之差小于第三边,同时考虑到两个分力同向或反向的情况.当两个分力同向时(均指向正右边),有最长的合力线段,其大小为F合=F1+F2;当两个分力反向时(F2指向正右边、F1指向正左边),有最短的合力线段,其大小为F合=F1-F2.故合力与分力的大小关系为:|F1-F2|≤F合≤F1+F2. 【点评】 深刻理解平行四边形定则与三角形定则是解答本题的关键.合力的取值范围也可通过公式 得到.第3讲 重点探究 变式题 如右图所示,AB为半圆的一条直径, AO=OB,P点为圆周上的一点,在P点作用了三个共点力F1、F2、F3,已知F2,则它们的合力为 . 【解析】由题意可知,三个共点力F1、F2、F3的大小、方向,相互之间的夹角均不明确,因此,运用力的合成公式求解,是不可能求得合力的,这就必须运用几何方法求合力,思考问题时,应着重分析圆的几何特点.第3讲 重点探究 如右图所示,将半圆补成完整的圆,延长PO交圆周于C点,连接AC、BC,易知:四边形PACB为平行四边形.所以,
F1、F3的合力为2F2,则这三个力的合力为3F2. 【点评】 本题注重数形结合,考查利用数学知识分析物理问题的能力.其中在力的图示中,凡涉及到特殊几何图形,一定要利用特殊几何图形的几何特征求解有关力的大小. 【答案】 3F2第3讲 重点探究探究点二 求合力的方法与技巧 例2 如右图所示,有五个力作用于同一点O,表示这五个力的有向线段恰分别构成一个正六边形的两邻边和三条对角线.已知F1=10N,试用多种方法求这五个力的合力. 【解析】方法一:利用平行四边形定则求解
将F5与F2、F4与F3合成,作出平行四边形如右图所示,它们的对角线对应的力的大小均等于F1,故这五个力的合力大小为3F1=30N.第3讲 重点探究 方法二:利用三角形法求解
将力F2、F3平移到F5与F1、F4与F1的末端之间,如右图所示.F3、F4的合力等于F1,F5、F2的合力等于F1,这五个力的合力大小为3F1=30 N.
方法三:利用正交分解法求解
将力F2、F3、F4、F5沿F1方向和垂直F1的方向分解,如右图所示.根据对称性知Fy=0, 合力F=Fx, F=
2F2cos60°+2F4cos30°+F1=30 N.第3讲 重点探究 方法四:利用公式法求解
因F1=10N,由几何关系不难求出,F5=F4= N、F2=F3=5N,将F5与F4、F2与F3组合求它们的合力,它们的夹角分别为60°和120°,由于两个相等力的合力可
由公式F合=2Fcos ,故它们的合力的大小为5N与15N,
方向沿F1的方向,所以这五个力的合力为30N. 【点评】 上述四种求合力的方法是中学阶段常用的四种方法,除此之外,常用的还有利用加速度求解的方法.第3讲 重点探究探究点三 力的效果分解法 例3 试作图,对下图中各物体的重力mg或作用力F进行有效分解,并求出其分力的大小.第3讲 重点探究 【解析】图A中,如右图所示,F的作用效果是使楔子向两个侧面挤压木材,由直角三角形知识知: (1)图A中,用竖直向下的作用力F将顶角为α的楔子,钉入木头中.
(2)图B中,用两轻绳OA与AB悬挂一个重球,现将AB绳剪断的瞬间.
(3)图C中,将重为mg的小球穿在光滑的杆AB上,并用轻绳OC拉住.第3讲 重点探究 图B中,如右图所示,剪
断拉绳AB的瞬时,重力的作
用效果:(1)继续对绳OA产
生拉力F1;(2)改变小球的
运动状态,使之开始绕O点做
圆周运动.
由图知:F1=mgcosα,F2=mgsinα.
图C中,如右图所示,重力既使物体
拉紧细绳,又使自身压紧杆AB,在mg、第3讲 重点探究 【点评】 一个力的分解有无数个分解方法,其中符合实际的有效分解具有唯一性.对力进行有效分解时要注意分解的步骤与原则.分解时,一般先考虑分力的方向,再考虑分力的大小.其中,分力的方向是由力的作用效果确定,分力的大小由平行四边形定则确定.F1、F2所组成的封闭三角形中,由正弦定理得:第3讲 重点探究探究点四 利用力的分解求极值 例4 如右图所示.已知质量为m、
电荷为q的小球,在匀强电场中由静止
释放后沿直线OP向斜下方运动(OP和
竖直方向成θ角),那么所加匀强电场
的场强E的最小值是多少? 【解析】 根据题意,释放后小球所受合力的方向必为OP方向.它的一个分力为重力,另一个分力为电场力,其中,合力与两个分力应构成一个力的三角形.第3讲 重点探究 用三角形定则从上图中不难看出:重力矢量OG的大小方向确定后,合力F的方向确定(为OP方向),而电场力Eq的矢量起点必须在G点,终点必须在OP射线上.在图中画出一组可能的电场力,不难看出,只有当电场力方向与
OP方向垂直时Eq才会最小,所以E也最小,有 【点评】 本题涉及到了一种很典型的力的分解,在习题中出现的频率较高,一般涉及三个力的作用,其中一个力的大小与方向不变,所求量为其中一个力的最小值.在利用力的分解时,可使用三角形定则作出力的动态变化的系列三角形,当其中一个分力与合力垂直时,这个分力取最小值.第3讲 重点探究 变式题 在“验证力的平行
四边形定则”的实验中,使b弹簧
测力计按如右图所示位置开始
顺时针缓慢转动,在这一过程
中保持O点位置不变和a弹簧测
力计的拉伸方向不变,则在整个过程中关于a、b弹簧测力计的读数变化是( )
?A. a增大,b减小
?B. a减小,b增大减小
?C. a减小,b先增大后减小
?D. a减小,b先减小后增大第3讲 重点探究 【解析】以结点O为研究对象,
因为O点的位置不变,所以,橡皮条
的拉力大小一定,方向一定,对应的
力为合力. 两个弹簧秤的弹力为分
力,合力与两个分力应构成一个力
的三角形.又a弹簧秤的弹力方向一
定,只有b弹簧秤的弹力大小方向均改变,故此题采用三角形定则的图解法较简单.作出力的矢量三角形如右图所示,从图中可以看出:在b弹簧顺时针缓慢转动过程中,a弹簧的弹力逐渐减小,b弹簧的弹力先减小后增大.当两弹簧秤垂直时,b弹簧秤的读数最小.第3讲 重点探究 【答案】 D 【点评】 在物体受三个力作用处于动态平衡时,若三个力中有两个力的方向改变但大小不变时,采用解析法较简便.当三个力没有哪两力大小相等,也没有哪两力方向垂直时,利用长度三角形与力的三角形的相似性列方程求解简便.当三个力中只有一个力的方向变化时,采用三角形图解法解题比较简便、直观.第3讲 重点探究
本讲复习要求理解合力与分力的关系;掌握力的平行四边形定则;会求两个力的合力;能够根据力的作用效果进行分解并求力;能够用正交分解法求出多个力的合力;能用“图解法”定性分析力的变化情况.
复习时,要求掌握求合力的四种常用的方法(公式法、平行四边形法、三角形法、正交分解法);掌握按效果分解的原则(效果确定方向、法则确定大小);会利用一种特殊类型的力的分解求极值.复习指南第3讲 课前热身 1. 下面关于合力与分力的叙述正确的是 ( )
?A. 一个物体受到几个力的作用,同时也受到这几个力的合力的作用
B. 几个力的合力总是大于它各个分力中最小的力
?C. 一个力分解成两个分力,可以得到无数对大小、方向不同的分力
?D. 合力和它相应的分力可以相互替代CD 2. 四个共点力的大小分别为2 N、3 N、4 N、6 N,它们的合力最大值为 15 N ,它们的合力最小值为 0 . 【解析】 它们的合力最大值Fmax=(2+3+4+6)N=
15 N.因为Fm=6N<(2+3+4)N,所以它们的合力最小值为0. 3. [2007届·长沙市一中模拟题]一运动员举起了367.5 kg的杠铃,如右图所示.杠铃静止时,运动员每个手臂承受的压力为(取g=10 m/s2) ( )B第3讲 课前热身 【解析】 运动员每个手臂承受的压力与手臂对扛铃的支持力是作用力与反作用力,杠铃处于平衡状态,其受力与合成如右图.
由几何关系得:2Fcos45°
=G,解得F=第3讲 课前热身 4. 如右图所示,直
立于地面的电线杆AB,
受到电线AD的水平拉力
为2×103 N,为使电线杆
不致倾斜,用钢索AC将A
端拉住,则钢索AC受到
的拉力FAC= N.
电线杆在A处受到 (选填“压力”、“拉力”)作用,大小为FA= N.第3讲 课前热身4×103压力3.46×103 【解析】钢索AC的拉
力产生沿水平方向拉杆和
沿竖直方向压杆两种效果,
因此,将其分解如右图所
示.由题意,电线杆不倾
斜有FACcos60°=2×103N,
FA=FACsin60°解得FAC=4×103N,FA=3.46×103N.第3讲 课前热身 5. 如右图所示,物体静止于光滑的水平面上,力F作用于物体O点,现要使合力沿着OO′方向,那么,必须同时再加一个力F′,这个力的最小值是 ( )B 【解析】 由上图可知,F′的最小值是Fsinθ,即B正确. ?A. Fcosθ ?B. Fsinθ
?C. Ftanθ ?D. Fcotθ第3讲 课前热身第3讲 考点整合 一、合力与分力的关系
1. 等效关系:合力与它的分力产生的作用效果完全相同.
2. 满足力的平行四边形定则:对角线对应合力、两邻边对应两分力(它还可衍生三角形定则).
3. 可相互替代:在研究力的作用效果时可以相互替代,体现了等效思想.
(1)用合力替代分力,要用到力的合成;
(2)用分力替代合力,要用到力的分解. 二、合力公式及其推论(已知F1、F2及θ)
合力公式:
推 论:第3讲 考点整合 三、力的分解(已知合力求分力的大小与方向)
1. 力的有效分解的原则:由合力产生的实际效果确定分力的方向,由平行四边形定则确定分力的大小.
2. 力的分解的三种类型: (1)已知合力和两个分力的方向,求两个分力的大小.(有唯一解)
(2)已知合力和一个分力的大小与方向,求另一分力的大小和方向.(有唯一解)
(3)已知合力、一个分力F1的大小与另一分力F2的方向,求F1的方向和F2的大小.(当F1=Fsinθ时,有唯一解;当Fsinθ<F1<F时,有两个解; 当F1>F时,分解是唯一的)
3. 力的正交分解法:将已知力按互相垂直的两个方向进行分解的方法.其目的是将不同方向的矢量运算简化为同一直线上的代数运算.第3讲 考点整合第3讲 重点探究探究点一 合力与分力的图示 例1 (1)指出图1-3-7所示每幅图中的合力与分力,并说明它们的关系. (2)如右图所示是力
的平行四边形定则示意
图.若力F1、F2大小不变,
F1的方向可在0°≤θ≤
180°范围内变化,以D为
圆心,以F1的大小AB为半径画半圆.则半圆上任一点与点A的连线表示怎样的物理意义?并结合该图谈谈合力与分力的关系.第3讲 重点探究 【解析】 (1)每幅图中的合力与分力及其关系分别是:
图A:由平行四边形定则可知,力F1、F2的合力为F3.
图B:由三角形定则可知,力F1、F2的合力为F3.
图C:由三角形定则可知,力F1、F3的合力为F2.
图D:由三角形定则可知,力F1、F2、F3的合力为零.
(2)两个不共线的共点力与它们的合力构成三角形,分力和合力的关系实际上就是三角形的一个边和其他两边的关系,题中所讲的半圆上任一点与第3讲 重点探究点A的连线表示F1、F2的合力.根据三角形两边之和应大于第三边.两边之差小于第三边,同时考虑到两个分力同向或反向的情况.当两个分力同向时(均指向正右边),有最长的合力线段,其大小为F合=F1+F2;当两个分力反向时(F2指向正右边、F1指向正左边),有最短的合力线段,其大小为F合=F1-F2.故合力与分力的大小关系为:|F1-F2|≤F合≤F1+F2. 【点评】 深刻理解平行四边形定则与三角形定则是解答本题的关键.合力的取值范围也可通过公式 得到.第3讲 重点探究 变式题 如右图所示,AB为半圆的一条直径, AO=OB,P点为圆周上的一点,在P点作用了三个共点力F1、F2、F3,已知F2,则它们的合力为 . 【解析】由题意可知,三个共点力F1、F2、F3的大小、方向,相互之间的夹角均不明确,因此,运用力的合成公式求解,是不可能求得合力的,这就必须运用几何方法求合力,思考问题时,应着重分析圆的几何特点.第3讲 重点探究 如右图所示,将半圆补成完整的圆,延长PO交圆周于C点,连接AC、BC,易知:四边形PACB为平行四边形.所以,
F1、F3的合力为2F2,则这三个力的合力为3F2. 【点评】 本题注重数形结合,考查利用数学知识分析物理问题的能力.其中在力的图示中,凡涉及到特殊几何图形,一定要利用特殊几何图形的几何特征求解有关力的大小. 【答案】 3F2第3讲 重点探究探究点二 求合力的方法与技巧 例2 如右图所示,有五个力作用于同一点O,表示这五个力的有向线段恰分别构成一个正六边形的两邻边和三条对角线.已知F1=10N,试用多种方法求这五个力的合力. 【解析】方法一:利用平行四边形定则求解
将F5与F2、F4与F3合成,作出平行四边形如右图所示,它们的对角线对应的力的大小均等于F1,故这五个力的合力大小为3F1=30N.第3讲 重点探究 方法二:利用三角形法求解
将力F2、F3平移到F5与F1、F4与F1的末端之间,如右图所示.F3、F4的合力等于F1,F5、F2的合力等于F1,这五个力的合力大小为3F1=30 N.
方法三:利用正交分解法求解
将力F2、F3、F4、F5沿F1方向和垂直F1的方向分解,如右图所示.根据对称性知Fy=0, 合力F=Fx, F=
2F2cos60°+2F4cos30°+F1=30 N.第3讲 重点探究 方法四:利用公式法求解
因F1=10N,由几何关系不难求出,F5=F4= N、F2=F3=5N,将F5与F4、F2与F3组合求它们的合力,它们的夹角分别为60°和120°,由于两个相等力的合力可
由公式F合=2Fcos ,故它们的合力的大小为5N与15N,
方向沿F1的方向,所以这五个力的合力为30N. 【点评】 上述四种求合力的方法是中学阶段常用的四种方法,除此之外,常用的还有利用加速度求解的方法.第3讲 重点探究探究点三 力的效果分解法 例3 试作图,对下图中各物体的重力mg或作用力F进行有效分解,并求出其分力的大小.第3讲 重点探究 【解析】图A中,如右图所示,F的作用效果是使楔子向两个侧面挤压木材,由直角三角形知识知: (1)图A中,用竖直向下的作用力F将顶角为α的楔子,钉入木头中.
(2)图B中,用两轻绳OA与AB悬挂一个重球,现将AB绳剪断的瞬间.
(3)图C中,将重为mg的小球穿在光滑的杆AB上,并用轻绳OC拉住.第3讲 重点探究 图B中,如右图所示,剪
断拉绳AB的瞬时,重力的作
用效果:(1)继续对绳OA产
生拉力F1;(2)改变小球的
运动状态,使之开始绕O点做
圆周运动.
由图知:F1=mgcosα,F2=mgsinα.
图C中,如右图所示,重力既使物体
拉紧细绳,又使自身压紧杆AB,在mg、第3讲 重点探究 【点评】 一个力的分解有无数个分解方法,其中符合实际的有效分解具有唯一性.对力进行有效分解时要注意分解的步骤与原则.分解时,一般先考虑分力的方向,再考虑分力的大小.其中,分力的方向是由力的作用效果确定,分力的大小由平行四边形定则确定.F1、F2所组成的封闭三角形中,由正弦定理得:第3讲 重点探究探究点四 利用力的分解求极值 例4 如右图所示.已知质量为m、
电荷为q的小球,在匀强电场中由静止
释放后沿直线OP向斜下方运动(OP和
竖直方向成θ角),那么所加匀强电场
的场强E的最小值是多少? 【解析】 根据题意,释放后小球所受合力的方向必为OP方向.它的一个分力为重力,另一个分力为电场力,其中,合力与两个分力应构成一个力的三角形.第3讲 重点探究 用三角形定则从上图中不难看出:重力矢量OG的大小方向确定后,合力F的方向确定(为OP方向),而电场力Eq的矢量起点必须在G点,终点必须在OP射线上.在图中画出一组可能的电场力,不难看出,只有当电场力方向与
OP方向垂直时Eq才会最小,所以E也最小,有 【点评】 本题涉及到了一种很典型的力的分解,在习题中出现的频率较高,一般涉及三个力的作用,其中一个力的大小与方向不变,所求量为其中一个力的最小值.在利用力的分解时,可使用三角形定则作出力的动态变化的系列三角形,当其中一个分力与合力垂直时,这个分力取最小值.第3讲 重点探究 变式题 在“验证力的平行
四边形定则”的实验中,使b弹簧
测力计按如右图所示位置开始
顺时针缓慢转动,在这一过程
中保持O点位置不变和a弹簧测
力计的拉伸方向不变,则在整个过程中关于a、b弹簧测力计的读数变化是( )
?A. a增大,b减小
?B. a减小,b增大减小
?C. a减小,b先增大后减小
?D. a减小,b先减小后增大第3讲 重点探究 【解析】以结点O为研究对象,
因为O点的位置不变,所以,橡皮条
的拉力大小一定,方向一定,对应的
力为合力. 两个弹簧秤的弹力为分
力,合力与两个分力应构成一个力
的三角形.又a弹簧秤的弹力方向一
定,只有b弹簧秤的弹力大小方向均改变,故此题采用三角形定则的图解法较简单.作出力的矢量三角形如右图所示,从图中可以看出:在b弹簧顺时针缓慢转动过程中,a弹簧的弹力逐渐减小,b弹簧的弹力先减小后增大.当两弹簧秤垂直时,b弹簧秤的读数最小.第3讲 重点探究 【答案】 D 【点评】 在物体受三个力作用处于动态平衡时,若三个力中有两个力的方向改变但大小不变时,采用解析法较简便.当三个力没有哪两力大小相等,也没有哪两力方向垂直时,利用长度三角形与力的三角形的相似性列方程求解简便.当三个力中只有一个力的方向变化时,采用三角形图解法解题比较简便、直观.第3讲 重点探究
同课章节目录
