2008高考一轮复习课件--第4讲 物体的平衡[上学期]
文档属性
| 名称 | 2008高考一轮复习课件--第4讲 物体的平衡[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 645.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2007-08-13 00:00:00 | ||
图片预览










文档简介
课件38张PPT。第4讲 物体的平衡 物体的平衡为高考的一个热点内容,它不仅涉及力学范畴的物体的平衡,在气体压强的计算、带电粒子在复合场中的运动、电磁感应中的切割运动等内容中也有涉及.主要考查用正交分解法、三角形法处理共点力的平衡问题,用整体法和隔离法分析系统平衡问题,其题型主要是选择题.?
本讲复习要求理解共点力作用下物体的平衡条件,能够利用正交分解法、三角形法解决一个物体的共点力的平衡问题,会用整体法和隔离法分析简单的系统平衡问题.
复习时,要求透彻理解F合=0及其相关结论.会用几种常用方法(合成法、正交分解法、效果分解法、三角形法)解答三力平衡问题;会用动态三角形解答三力的动态平衡问题;会用正交分解法与合成法解答三力以上的平衡问题.知道系统平衡的条件,领会整体法和隔离法,会解答系统平衡问题.复习指南第4讲 课前热身 1. 以下四种情况中,物体处于平衡状态的有( )
?A. 竖直上抛物体达最高点时
?B. 做匀速圆周运动的物体
?C. 单摆摆球通过平衡位置时
?D. 弹簧振子通过平衡位置时D 【解析】 判断物体是否处于平衡状态的标准是:物体的加速度是否为0. 2.现有共点的五个力平衡,则下列说法不正确的是
( )
?A. 其中四个力的合力与第五个力等大反向
?B. 其中三个力的合力与其余的两个力的合力等大反向D ?C. 五个力首尾相接,构成封闭的五边形
?D. 撤去其中的三个力,物体一定不平衡
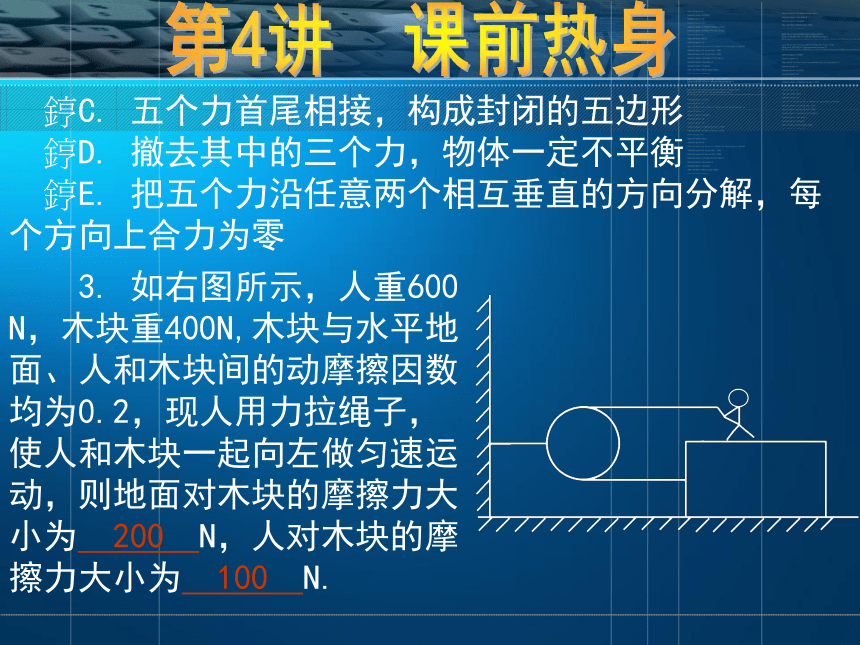
?E. 把五个力沿任意两个相互垂直的方向分解,每个方向上合力为零 3. 如右图所示,人重600N,木块重400N,木块与水平地面、人和木块间的动摩擦因数均为0.2,现人用力拉绳子,使人和木块一起向左做匀速运动,则地面对木块的摩擦力大小为 200 N,人对木块的摩擦力大小为 100 N.第4讲 课前热身 4. [2007届·江苏模拟题]
如下图所示,半径为R、内壁光
滑的空心圆筒放在地上,将两个
重力都是G、半径都是r的球(R
<2r<2R)放在圆筒中,下列说
法正确的是 ( )
A. 筒底对球A的弹力一定等于2G
? B. 筒壁对球A的弹力等于筒壁对球B的弹力大小
?C. 球A对球B的弹力一定大于重力G
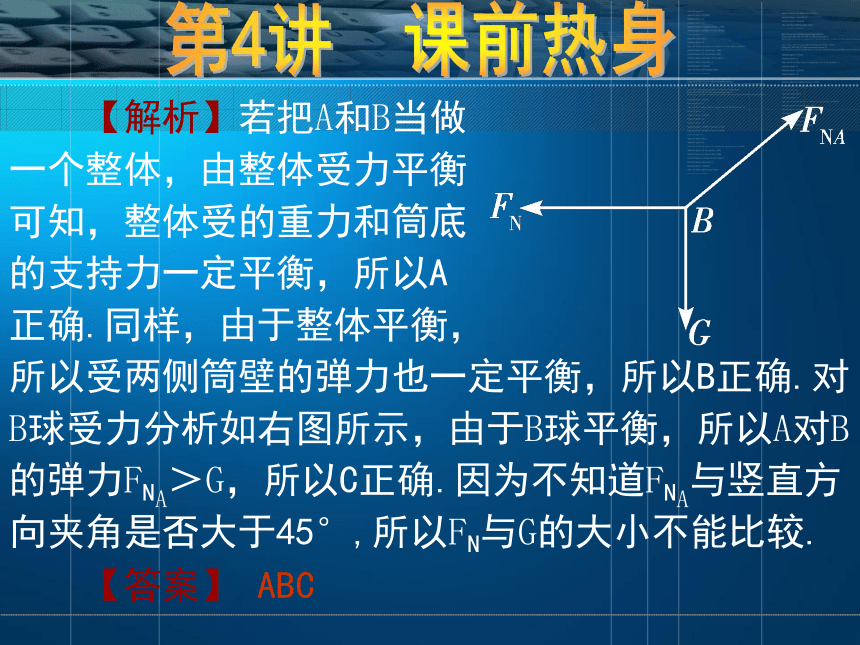
?D. 球B对筒壁的压力一定小于重力G第4讲 课前热身 【解析】若把A和B当做
一个整体,由整体受力平衡
可知,整体受的重力和筒底
的支持力一定平衡,所以A
正确.同样,由于整体平衡,
所以受两侧筒壁的弹力也一定平衡,所以B正确.对B球受力分析如右图所示,由于B球平衡,所以A对B的弹力FNA>G,所以C正确.因为不知道FNA与竖直方向夹角是否大于45°,所以FN与G的大小不能比较. 【答案】 ABC第4讲 课前热身 5. 用与竖直方向成α=30°斜向右上方,大小为F的推力把一个重量为G的木块压在粗糙竖直墙上保持静止.求墙对木块的正压力大小FN和墙对木块的摩擦力大小Ff. 【解析】 分析木块受力知,重力为G,竖直向下,推力F与竖直成30°斜向右上方,墙对木块的弹力
大小跟F的水平分力平衡,所以FN= ,墙对木块的摩擦
力是静摩擦力,其大小和方向由F的竖直分力和重力大
小的关系而决定,由正交分解法可以得出:第4讲 课前热身第4讲 考点整合 一、物体受共点力作用下的平衡
平衡标志:物体的加速度为0(物体处于静止或匀速直线运动状态叫做平衡状态).
平衡条件:作用在物体上的合外力F合=0,它有如下推论:
(1)沿任意方向,物体的合分力为0.
(2)若将物体的受力正交分解,则有
(3)若受两力处于平衡状态,则两个力大小相
等、方向相反. (4)若受三个力作用而处于平衡状态, 则其中任意两个力的合力与第三个力大小相等、方向相反,且这三个力首尾相接构成封闭式三角形.
(5)若受N个作用力而处于平衡状态,则其中任意一个力与其余N-1个力的合力大小相等、方向相反,且这N个力首尾相接构成封闭式多边形.
(6)如果物体受三个不平行外力作用而平衡,这三个力的作用线必在同一平面上,而且必为共点力.
解题方法: (1)物体受二力作用:利用二力平衡条件解答.第4讲 考点整合 (2)物体受三力作用:常用有合成法、正交分解法、效果分解法、三角形法、力矩平衡法等解法,还可考虑用余弦定理、拉密定理、正弦定理等方法求解.
(3)物体受三个以上力作用: 常用解法有正交分解法、合成法等.
二、系统的平衡
平衡标志:系统内的每一个物体的加速度为0(静止或匀速直线运动).
平衡条件:作用在系统的合外力F合=0,合力矩M合=0.第4讲 考点整合 解题方法:正交分解法: (常用整体法
考虑系统受到的外力,并结合隔离法辅助求解).
(1)整体法:以分析系统所受外力为前提的求解力的平衡问题的方法.其优越性是其无须考虑系统的内力而使解答过程简便快捷,其不足之处是不能求解系统的内力.
(2)隔离法:以分析系统内的物体的受力为前提的求解力的平衡问题的方法.这种方法通常要列方程组求解,因而比较繁琐.第4讲 考点整合第4讲 重点探究探究点一 运用正交分解法解答物体的平衡问题 例1 [2007届·陕西模
拟题]一表面粗糙的斜面,
放在水平光滑的地面上,如
右图所示,θ为斜面的倾角.
一质量为m的滑块恰好能沿
斜面匀速下滑.若一推力F作用于滑块上使之沿斜面匀速上滑,为了保持斜面静止不动,必须用一大小为F′=4 mgcosθsinθ的水平力作用于斜面上,求推力F的大小和方向. 【解析】因物块恰好能够沿斜面下滑,设斜面与物块间的动摩擦因数为μ,则可得到:
mgsinθ=μmgcosθ,则μ=tanθ.
设推力F沿斜面的分量为Fx,垂直于斜面的方向的分量为Fy,滑块的受力分析如下图(a)所示,其中支持力为F1、摩擦力为F2.根据平衡条件列出方程:
x方向;Fx=mgsinθ+F2
y方向:F1=Fy+mgcosθ
F2=μF1.
斜面的受力如下图(b)所示,因斜面静止,故有F′=F2cosθ+F1sinθ.第4讲 重点探究第4讲 重点探究 【点评】 1. 利用正交分解法,要注意建立坐标轴的技巧,通常以解题的简便性为原则,应尽可能让较多的力坐落在坐标轴上.
2. 利用正交分解法建立方程组时,对物体受滑动摩擦力的情况,通常还要用到一个辅助方程,即为Ff=μFN.第4讲 重点探究探究点二 运用相似三角形求解三力平衡问题 例2 电梯修理员或牵引专家常常需要监测金属绳中的张力,但不能到绳的自由端去直接测量.某公司制造出一种能测量绳中张力的仪器,工作原理如下图所示,将相距为L的两根固定支柱A、B(图中小圆框表示支柱的横截面)垂直于金属绳水平放置,在AB的中点用一可动支柱C向上推动金属绳,使绳在垂直于AB的方向竖直向上发生一个偏移量d(d< (2)如果偏移量d=10 mm,作用力F=400 N,
L=250 mm,计算绳中张力的大小. 【解析】 (1)设C′点受两边绳的张力为FT1和FT2,AB与C′B的夹角为θ,如下图所示.
依对称性有:FT1=FT2=FT由力的合成有:F=2FTsinθ.第4讲 重点探究第4讲 重点探究 【点评】 力的三角形与对应的几何三角形具有方向对应、大小成正比的关系,所以,求力的问题可转化为求几何三角形的边角问题,运用相似三角形关系求力的大小与方向正是利用了上述关系.解题的关键是在作出力的图示后,分析力与线段的对应关系.第4讲 重点探究 变式题 如图(a)所示,半径为R、重为G的均匀球体靠竖直墙放置,在球体的左下方有一高为
h的木块.若一切摩擦不计,至少用多大的水平推力F推木块,才能使球体离开地面?(h<R)第4讲 重点探究 【解析】 球体刚好离开地面时,水平推力最小.球离开地面临界条件是球对地面的压力为零,而此时,球和木块的位置都没有改变.
当球刚脱离地面时,球受力如图(b)所示,选球为研究对象,力FN1、G、FN平移构成的力三角形与△OAB相似,由相似三角形知识得:第4讲 重点探究 选球和木块构成整体为研究对象,整体水平方向受两个力,即FN1和F,据平衡条件得:
F=FN1,即F=FN1= 【点评】 运用相似三角形法求力的大小时,若遇到的三角形为特殊三角形,一定要利用其特殊的几何关系求解.本题就利用了直角三角形所满足的勾股定理求边长的长度.第4讲 重点探究探究点三 运用力的动态三角形分析三力平衡问题 例3 如右图所示,轻绳AO、BO结于O点,系住一个质量为m的物体,AO、BO与竖直方向分别成α、β角,开始时α+β<90°.现保持O点位置不变,缓慢增加BO与竖直方向的夹角β,直到BO成水平方向,试讨论这一过程中绳AO及BO上的拉力各如何变化.第4讲 重点探究 【解析】 本题可先画出力的
矢量三角形,由几何关系来分析三角
形的变化,从而推断出力的大小、方
向的变化.
结点O所受拉力FT=mg,FTOA、
FTOB组成如右图所示三角形. 由图可
以看出,由于β角增大,开始阶段FTOB逐渐减小;当FTOB垂直FTOA时,FTOB最小;然后FTOB又逐渐增大,FTOA是一直增大.第4讲 重点探究 【点评】 1. 当物体受三力平衡时,其合力为0,这三个力构成封闭式三角形.若物体处于三力动态平衡时,这三个力构成封闭的移动式三角形,从三角形的变化之中,我们可找出力的变化规律.
2. 在一系列封闭的移动式三角形中,常见的力取最小值的情况是:当变力与特定方向垂直时,此变力取最小值.第4讲 重点探究探究点四 系统平衡问题 例4 有一个直角支架AOB,
AO水平放置,表面粗糙,OB竖直
放置,表面光滑.AO上套有小环P,
OB上套有小环Q,两环质量均为m,
两环间有一质量可忽略、 不可伸
长的细绳相连,并在某一位置平衡
(如右图所示).现将P环向左移一小段距离,两环再次达到平衡,那么将移动后的平衡状态和原来的平衡状态比较,AO杆对P环的支持力FN和细绳上的拉力FT的变化情况是 ( )第4讲 重点探究? A. FN不变,FT变大 ?B. FN不变,FT变小
?C. FN变大,FT变大 D. FN变大,FT变小 【解析】 本题中涉及到多个物体的平衡,我们采用的最佳解法是运用整体法和隔离法结合求解.
以两环与绳为系统作为研究对象,设绳与竖直方向夹角为θ,对系统而言,竖直方向受2mg的重力和
OA杆对环P的支持力FN,由力的平衡关系有:FN=2mg,故FN不变.
隔离Q环,它受三力作用,竖直方向满足:FTcosθ
=mg,FT= .P环左移,θ减小,FT变小,故选项B
正确.第4讲 重点探究 【答案】 B 【点评】 系统平衡的标志是系统内的每一个物体均处于平衡状态,若系统处于平衡或动态平衡,并且所求力为系统的外力,宜用整体法求解;若所求力是系统的内力,宜先用整体法求出外力,再用隔离法求出内力.第4讲 重点探究 变式题 如图(1)所示,质量为M的直角三棱柱A放在水平地面上,三棱柱的斜面是光滑的,且斜面倾角为θ.质量为m的光滑球B放在三棱柱和光滑竖直墙壁之间,A和B都处于静止状态,求地面对三棱柱支持力和摩擦力各为多少?(1) (2)第4讲 重点探究 【解析】选取A和B整体为研究对象,它受到重力(M+m)g,地面支持力FN,墙壁的弹力F和地面的摩擦力Ff的作用,现将系统所受的外力集中于一点,画出其受力示意图如图(2)所示,根据正交分解法有:
竖直方向:FN-(M+m)g=0,
水平方向:F=Ff,
可得FN=(M+m)g.
再隔离B进行研究,它受到重
力mg,三棱柱对它的支持力FNB,墙
壁对它的弹力F的作用(如右图所
示).根据正交分解法有:第4讲 重点探究 竖直方向:FNB·cosθ=mg,
水平方向:FNB·sinθ=F,
解得F=mgtanθ.
所以Ff=F=mgtanθ. 【点评】 多物体构成的系统若处于平衡状态, 则系统任意方向的合分力为0,解题时有两个习惯:(1)将所有系统的外力集中于一个作用点进行分析, 即当作一个物体来研究.(2)运用正交分解法对系统沿两个相互垂直方向列式求解.第4讲 重点探究探究点五 三力平衡问题的解题途径 例5 如右图所示,一个
半球形的碗放在桌面上,碗
口水平,O点为其球心,碗的
内表面及碗口是光滑的. 一
根细线跨在碗口上,线的两
端分别系有质量为m1和m2的小球,当它们处于平衡状态时,质量为m1的小球与O点的连线与水平线的夹角为α=60°.两小球的质量之比为( )第4讲 重点探究 【解析】 本题是一个三力平衡问
题,解法很多,其中常用的解法如下列
五种:
解法一:利用合成法求解
小球m1受FT、FN、m1g三力作用,受
力分析如右图所示.小球m1处于平衡状态,
故FN与FT的合力F=m1g.根据合力公式可得:
F= =m1g,第4讲 重点探究 将FN=FT=m2g,θ=60°代入上式解得:
故选项A正确.
解法二:利用力的三角形法求解
FN和FT的合力与小球m1g的重力大小
相等,方向相反,矢量三角形如右图所示.
由正弦定理得:第4讲 重点探究 解法三:利用正交分解法求解
如右图所示,以FN的方向为y轴,
以垂直于FN的方向为x轴建立坐标系.
因FN与FT的夹角为60°,则m1g与y轴
成30°角.在x轴方向由物体的平衡
条件有
m1gsin30°-FT·sin60°=0
故选项A正确.第4讲 重点探究 解法四:利用力的效果分解法求解
如右图所示.将重力m1g按其
作用效果分解为拉绳的分力FT′
与压碗的分力FN′,它们构成平
行四边形,由其中的三角形的边
角关系即可求出相同的结果,
具体解答略.第4讲 重点探究 解法五:利用力矩平衡法求解
如右图所示,反向延长
线m1g交OA于D;则BD⊥OA.
因△OAB是等边三角形,过
O点作AB的垂线交AB于E,
所以,∠AOB=∠OBA=60°.
设碗的半径为R,可得OD=
Rcos60°,OE=Rsin60°.以O点为固定转轴,根据力矩平衡条件,有m1g·OD=FT·OE. 第4讲 重点探究 解法六:利用拉密定理求解
如右图所示,对m1受力分析,
由题意可知:FT=m2g,α=60°,
β=γ=150°,根据拉密定理: 【答案】 A第4讲 重点探究 【点评】 (1)物体在三个
共点力作用下处于平衡状态,用
拉密定理来求解往往使复杂的问
题变得简单. 如右图所示,设三
力为F1、F2、F3,角度分别为α、
β、γ,则 如此例的解法六. (2)本
题除了可以用合成法、正交分解法、效果分解法、三
角形法、力矩平衡法、拉密定理求解外,还可考虑用余弦定理、正弦定理、整体法等方法求解.(3)力的平衡问题求解方法很多,它们均是基于物体所受的合力为0而衍生的解法,所以,这类问题的本质是物体所受合力为0.第4讲 重点探究
本讲复习要求理解共点力作用下物体的平衡条件,能够利用正交分解法、三角形法解决一个物体的共点力的平衡问题,会用整体法和隔离法分析简单的系统平衡问题.
复习时,要求透彻理解F合=0及其相关结论.会用几种常用方法(合成法、正交分解法、效果分解法、三角形法)解答三力平衡问题;会用动态三角形解答三力的动态平衡问题;会用正交分解法与合成法解答三力以上的平衡问题.知道系统平衡的条件,领会整体法和隔离法,会解答系统平衡问题.复习指南第4讲 课前热身 1. 以下四种情况中,物体处于平衡状态的有( )
?A. 竖直上抛物体达最高点时
?B. 做匀速圆周运动的物体
?C. 单摆摆球通过平衡位置时
?D. 弹簧振子通过平衡位置时D 【解析】 判断物体是否处于平衡状态的标准是:物体的加速度是否为0. 2.现有共点的五个力平衡,则下列说法不正确的是
( )
?A. 其中四个力的合力与第五个力等大反向
?B. 其中三个力的合力与其余的两个力的合力等大反向D ?C. 五个力首尾相接,构成封闭的五边形
?D. 撤去其中的三个力,物体一定不平衡
?E. 把五个力沿任意两个相互垂直的方向分解,每个方向上合力为零 3. 如右图所示,人重600N,木块重400N,木块与水平地面、人和木块间的动摩擦因数均为0.2,现人用力拉绳子,使人和木块一起向左做匀速运动,则地面对木块的摩擦力大小为 200 N,人对木块的摩擦力大小为 100 N.第4讲 课前热身 4. [2007届·江苏模拟题]
如下图所示,半径为R、内壁光
滑的空心圆筒放在地上,将两个
重力都是G、半径都是r的球(R
<2r<2R)放在圆筒中,下列说
法正确的是 ( )
A. 筒底对球A的弹力一定等于2G
? B. 筒壁对球A的弹力等于筒壁对球B的弹力大小
?C. 球A对球B的弹力一定大于重力G
?D. 球B对筒壁的压力一定小于重力G第4讲 课前热身 【解析】若把A和B当做
一个整体,由整体受力平衡
可知,整体受的重力和筒底
的支持力一定平衡,所以A
正确.同样,由于整体平衡,
所以受两侧筒壁的弹力也一定平衡,所以B正确.对B球受力分析如右图所示,由于B球平衡,所以A对B的弹力FNA>G,所以C正确.因为不知道FNA与竖直方向夹角是否大于45°,所以FN与G的大小不能比较. 【答案】 ABC第4讲 课前热身 5. 用与竖直方向成α=30°斜向右上方,大小为F的推力把一个重量为G的木块压在粗糙竖直墙上保持静止.求墙对木块的正压力大小FN和墙对木块的摩擦力大小Ff. 【解析】 分析木块受力知,重力为G,竖直向下,推力F与竖直成30°斜向右上方,墙对木块的弹力
大小跟F的水平分力平衡,所以FN= ,墙对木块的摩擦
力是静摩擦力,其大小和方向由F的竖直分力和重力大
小的关系而决定,由正交分解法可以得出:第4讲 课前热身第4讲 考点整合 一、物体受共点力作用下的平衡
平衡标志:物体的加速度为0(物体处于静止或匀速直线运动状态叫做平衡状态).
平衡条件:作用在物体上的合外力F合=0,它有如下推论:
(1)沿任意方向,物体的合分力为0.
(2)若将物体的受力正交分解,则有
(3)若受两力处于平衡状态,则两个力大小相
等、方向相反. (4)若受三个力作用而处于平衡状态, 则其中任意两个力的合力与第三个力大小相等、方向相反,且这三个力首尾相接构成封闭式三角形.
(5)若受N个作用力而处于平衡状态,则其中任意一个力与其余N-1个力的合力大小相等、方向相反,且这N个力首尾相接构成封闭式多边形.
(6)如果物体受三个不平行外力作用而平衡,这三个力的作用线必在同一平面上,而且必为共点力.
解题方法: (1)物体受二力作用:利用二力平衡条件解答.第4讲 考点整合 (2)物体受三力作用:常用有合成法、正交分解法、效果分解法、三角形法、力矩平衡法等解法,还可考虑用余弦定理、拉密定理、正弦定理等方法求解.
(3)物体受三个以上力作用: 常用解法有正交分解法、合成法等.
二、系统的平衡
平衡标志:系统内的每一个物体的加速度为0(静止或匀速直线运动).
平衡条件:作用在系统的合外力F合=0,合力矩M合=0.第4讲 考点整合 解题方法:正交分解法: (常用整体法
考虑系统受到的外力,并结合隔离法辅助求解).
(1)整体法:以分析系统所受外力为前提的求解力的平衡问题的方法.其优越性是其无须考虑系统的内力而使解答过程简便快捷,其不足之处是不能求解系统的内力.
(2)隔离法:以分析系统内的物体的受力为前提的求解力的平衡问题的方法.这种方法通常要列方程组求解,因而比较繁琐.第4讲 考点整合第4讲 重点探究探究点一 运用正交分解法解答物体的平衡问题 例1 [2007届·陕西模
拟题]一表面粗糙的斜面,
放在水平光滑的地面上,如
右图所示,θ为斜面的倾角.
一质量为m的滑块恰好能沿
斜面匀速下滑.若一推力F作用于滑块上使之沿斜面匀速上滑,为了保持斜面静止不动,必须用一大小为F′=4 mgcosθsinθ的水平力作用于斜面上,求推力F的大小和方向. 【解析】因物块恰好能够沿斜面下滑,设斜面与物块间的动摩擦因数为μ,则可得到:
mgsinθ=μmgcosθ,则μ=tanθ.
设推力F沿斜面的分量为Fx,垂直于斜面的方向的分量为Fy,滑块的受力分析如下图(a)所示,其中支持力为F1、摩擦力为F2.根据平衡条件列出方程:
x方向;Fx=mgsinθ+F2
y方向:F1=Fy+mgcosθ
F2=μF1.
斜面的受力如下图(b)所示,因斜面静止,故有F′=F2cosθ+F1sinθ.第4讲 重点探究第4讲 重点探究 【点评】 1. 利用正交分解法,要注意建立坐标轴的技巧,通常以解题的简便性为原则,应尽可能让较多的力坐落在坐标轴上.
2. 利用正交分解法建立方程组时,对物体受滑动摩擦力的情况,通常还要用到一个辅助方程,即为Ff=μFN.第4讲 重点探究探究点二 运用相似三角形求解三力平衡问题 例2 电梯修理员或牵引专家常常需要监测金属绳中的张力,但不能到绳的自由端去直接测量.某公司制造出一种能测量绳中张力的仪器,工作原理如下图所示,将相距为L的两根固定支柱A、B(图中小圆框表示支柱的横截面)垂直于金属绳水平放置,在AB的中点用一可动支柱C向上推动金属绳,使绳在垂直于AB的方向竖直向上发生一个偏移量d(d<
L=250 mm,计算绳中张力的大小. 【解析】 (1)设C′点受两边绳的张力为FT1和FT2,AB与C′B的夹角为θ,如下图所示.
依对称性有:FT1=FT2=FT由力的合成有:F=2FTsinθ.第4讲 重点探究第4讲 重点探究 【点评】 力的三角形与对应的几何三角形具有方向对应、大小成正比的关系,所以,求力的问题可转化为求几何三角形的边角问题,运用相似三角形关系求力的大小与方向正是利用了上述关系.解题的关键是在作出力的图示后,分析力与线段的对应关系.第4讲 重点探究 变式题 如图(a)所示,半径为R、重为G的均匀球体靠竖直墙放置,在球体的左下方有一高为
h的木块.若一切摩擦不计,至少用多大的水平推力F推木块,才能使球体离开地面?(h<R)第4讲 重点探究 【解析】 球体刚好离开地面时,水平推力最小.球离开地面临界条件是球对地面的压力为零,而此时,球和木块的位置都没有改变.
当球刚脱离地面时,球受力如图(b)所示,选球为研究对象,力FN1、G、FN平移构成的力三角形与△OAB相似,由相似三角形知识得:第4讲 重点探究 选球和木块构成整体为研究对象,整体水平方向受两个力,即FN1和F,据平衡条件得:
F=FN1,即F=FN1= 【点评】 运用相似三角形法求力的大小时,若遇到的三角形为特殊三角形,一定要利用其特殊的几何关系求解.本题就利用了直角三角形所满足的勾股定理求边长的长度.第4讲 重点探究探究点三 运用力的动态三角形分析三力平衡问题 例3 如右图所示,轻绳AO、BO结于O点,系住一个质量为m的物体,AO、BO与竖直方向分别成α、β角,开始时α+β<90°.现保持O点位置不变,缓慢增加BO与竖直方向的夹角β,直到BO成水平方向,试讨论这一过程中绳AO及BO上的拉力各如何变化.第4讲 重点探究 【解析】 本题可先画出力的
矢量三角形,由几何关系来分析三角
形的变化,从而推断出力的大小、方
向的变化.
结点O所受拉力FT=mg,FTOA、
FTOB组成如右图所示三角形. 由图可
以看出,由于β角增大,开始阶段FTOB逐渐减小;当FTOB垂直FTOA时,FTOB最小;然后FTOB又逐渐增大,FTOA是一直增大.第4讲 重点探究 【点评】 1. 当物体受三力平衡时,其合力为0,这三个力构成封闭式三角形.若物体处于三力动态平衡时,这三个力构成封闭的移动式三角形,从三角形的变化之中,我们可找出力的变化规律.
2. 在一系列封闭的移动式三角形中,常见的力取最小值的情况是:当变力与特定方向垂直时,此变力取最小值.第4讲 重点探究探究点四 系统平衡问题 例4 有一个直角支架AOB,
AO水平放置,表面粗糙,OB竖直
放置,表面光滑.AO上套有小环P,
OB上套有小环Q,两环质量均为m,
两环间有一质量可忽略、 不可伸
长的细绳相连,并在某一位置平衡
(如右图所示).现将P环向左移一小段距离,两环再次达到平衡,那么将移动后的平衡状态和原来的平衡状态比较,AO杆对P环的支持力FN和细绳上的拉力FT的变化情况是 ( )第4讲 重点探究? A. FN不变,FT变大 ?B. FN不变,FT变小
?C. FN变大,FT变大 D. FN变大,FT变小 【解析】 本题中涉及到多个物体的平衡,我们采用的最佳解法是运用整体法和隔离法结合求解.
以两环与绳为系统作为研究对象,设绳与竖直方向夹角为θ,对系统而言,竖直方向受2mg的重力和
OA杆对环P的支持力FN,由力的平衡关系有:FN=2mg,故FN不变.
隔离Q环,它受三力作用,竖直方向满足:FTcosθ
=mg,FT= .P环左移,θ减小,FT变小,故选项B
正确.第4讲 重点探究 【答案】 B 【点评】 系统平衡的标志是系统内的每一个物体均处于平衡状态,若系统处于平衡或动态平衡,并且所求力为系统的外力,宜用整体法求解;若所求力是系统的内力,宜先用整体法求出外力,再用隔离法求出内力.第4讲 重点探究 变式题 如图(1)所示,质量为M的直角三棱柱A放在水平地面上,三棱柱的斜面是光滑的,且斜面倾角为θ.质量为m的光滑球B放在三棱柱和光滑竖直墙壁之间,A和B都处于静止状态,求地面对三棱柱支持力和摩擦力各为多少?(1) (2)第4讲 重点探究 【解析】选取A和B整体为研究对象,它受到重力(M+m)g,地面支持力FN,墙壁的弹力F和地面的摩擦力Ff的作用,现将系统所受的外力集中于一点,画出其受力示意图如图(2)所示,根据正交分解法有:
竖直方向:FN-(M+m)g=0,
水平方向:F=Ff,
可得FN=(M+m)g.
再隔离B进行研究,它受到重
力mg,三棱柱对它的支持力FNB,墙
壁对它的弹力F的作用(如右图所
示).根据正交分解法有:第4讲 重点探究 竖直方向:FNB·cosθ=mg,
水平方向:FNB·sinθ=F,
解得F=mgtanθ.
所以Ff=F=mgtanθ. 【点评】 多物体构成的系统若处于平衡状态, 则系统任意方向的合分力为0,解题时有两个习惯:(1)将所有系统的外力集中于一个作用点进行分析, 即当作一个物体来研究.(2)运用正交分解法对系统沿两个相互垂直方向列式求解.第4讲 重点探究探究点五 三力平衡问题的解题途径 例5 如右图所示,一个
半球形的碗放在桌面上,碗
口水平,O点为其球心,碗的
内表面及碗口是光滑的. 一
根细线跨在碗口上,线的两
端分别系有质量为m1和m2的小球,当它们处于平衡状态时,质量为m1的小球与O点的连线与水平线的夹角为α=60°.两小球的质量之比为( )第4讲 重点探究 【解析】 本题是一个三力平衡问
题,解法很多,其中常用的解法如下列
五种:
解法一:利用合成法求解
小球m1受FT、FN、m1g三力作用,受
力分析如右图所示.小球m1处于平衡状态,
故FN与FT的合力F=m1g.根据合力公式可得:
F= =m1g,第4讲 重点探究 将FN=FT=m2g,θ=60°代入上式解得:
故选项A正确.
解法二:利用力的三角形法求解
FN和FT的合力与小球m1g的重力大小
相等,方向相反,矢量三角形如右图所示.
由正弦定理得:第4讲 重点探究 解法三:利用正交分解法求解
如右图所示,以FN的方向为y轴,
以垂直于FN的方向为x轴建立坐标系.
因FN与FT的夹角为60°,则m1g与y轴
成30°角.在x轴方向由物体的平衡
条件有
m1gsin30°-FT·sin60°=0
故选项A正确.第4讲 重点探究 解法四:利用力的效果分解法求解
如右图所示.将重力m1g按其
作用效果分解为拉绳的分力FT′
与压碗的分力FN′,它们构成平
行四边形,由其中的三角形的边
角关系即可求出相同的结果,
具体解答略.第4讲 重点探究 解法五:利用力矩平衡法求解
如右图所示,反向延长
线m1g交OA于D;则BD⊥OA.
因△OAB是等边三角形,过
O点作AB的垂线交AB于E,
所以,∠AOB=∠OBA=60°.
设碗的半径为R,可得OD=
Rcos60°,OE=Rsin60°.以O点为固定转轴,根据力矩平衡条件,有m1g·OD=FT·OE. 第4讲 重点探究 解法六:利用拉密定理求解
如右图所示,对m1受力分析,
由题意可知:FT=m2g,α=60°,
β=γ=150°,根据拉密定理: 【答案】 A第4讲 重点探究 【点评】 (1)物体在三个
共点力作用下处于平衡状态,用
拉密定理来求解往往使复杂的问
题变得简单. 如右图所示,设三
力为F1、F2、F3,角度分别为α、
β、γ,则 如此例的解法六. (2)本
题除了可以用合成法、正交分解法、效果分解法、三
角形法、力矩平衡法、拉密定理求解外,还可考虑用余弦定理、正弦定理、整体法等方法求解.(3)力的平衡问题求解方法很多,它们均是基于物体所受的合力为0而衍生的解法,所以,这类问题的本质是物体所受合力为0.第4讲 重点探究
同课章节目录
