2018年北师大版数学七年级下册4.1.3三角形的重要线段课件 (共23张PPT)
文档属性
| 名称 | 2018年北师大版数学七年级下册4.1.3三角形的重要线段课件 (共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 585.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-03 15:09:49 | ||
图片预览





文档简介
课件23张PPT。4.1.3三角形的重要线段第四章 三角形 4.1认识三角形1.有 相等的三角形叫等腰三角形
有三边都相等的三角形式 三角形,也叫正三角形
2. 两边之和大于第三边。
两边之差小于第三边。
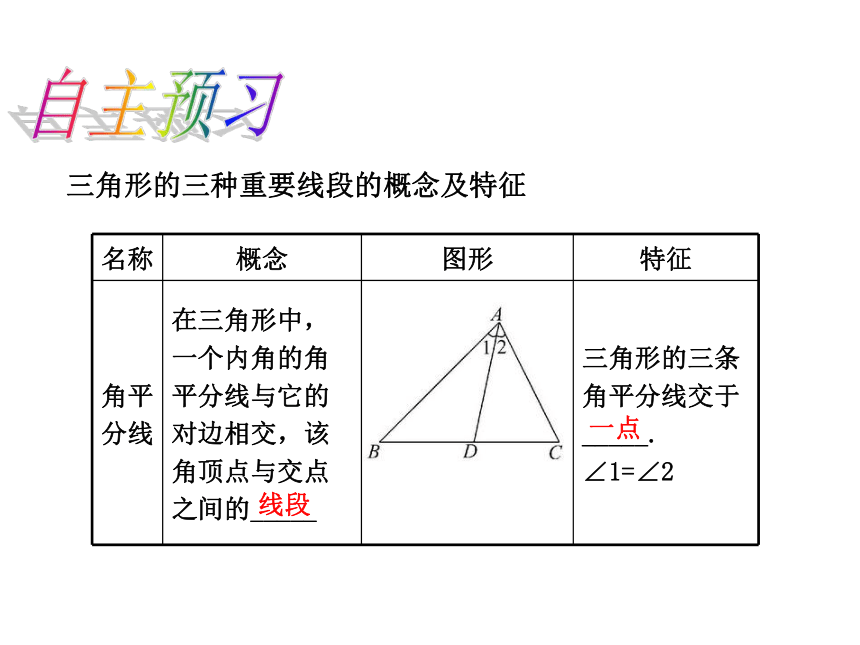
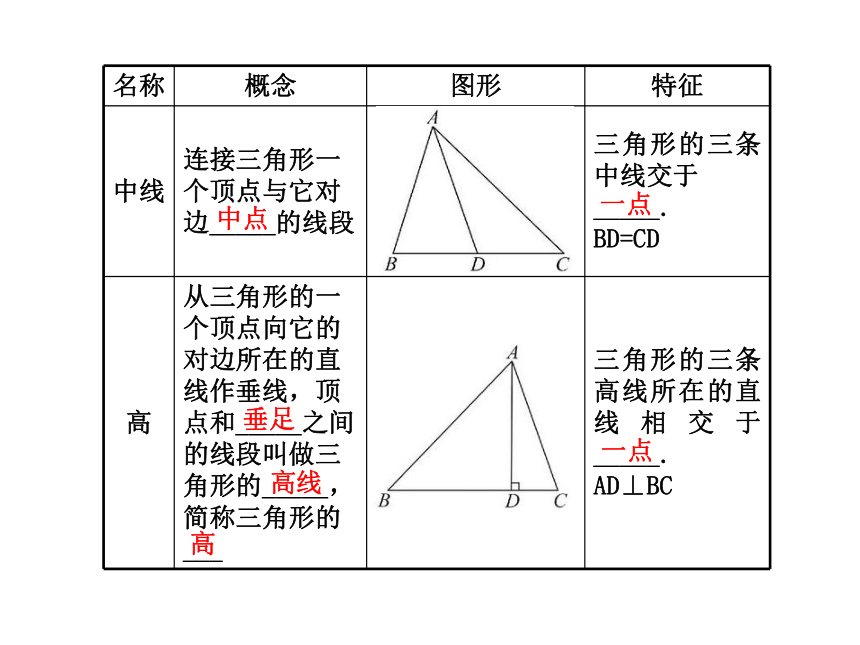
第三边大于两边之 ,小于两边之 。知识回顾三角形的三种重要线段的概念及特征 线段一点自主预习中点一点垂足高线高一点探究:三角形的三条高的关系:
如图,画出锐角三角形、直角
三角形和钝角三角形的三条高.
①锐角三角形的三条高相交于三角形___部的___个点.
②直角三角形的三条高相交于三角形的_________.
③钝角三角形的三条高所在直线相交于三角形___部的___个点.
【归纳】三角形的三条高所在的直线相交于一点.
【点拨】三角形的角平分线、高、中线都是线段.内一直角顶点外一【预习思考】
三角形的角平分线和角的平分线是一回事吗?
提示:不是.它们均平分一个角,但三角形的角平分线是一条线段,而角的平分线是一条射线. 三角形的三种重要线段区分
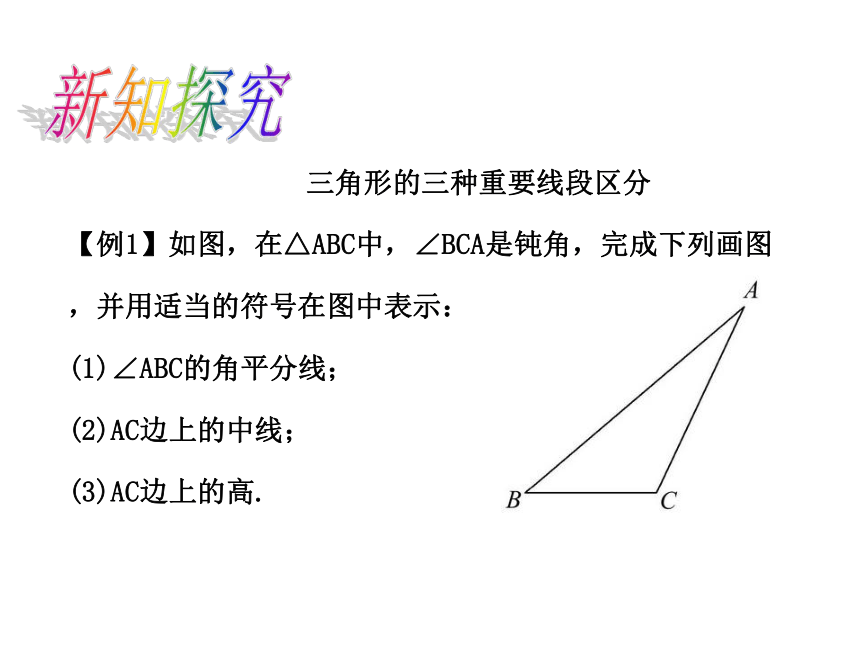
【例1】如图,在△ABC中,∠BCA是钝角,完成下列画图,并用适当的符号在图中表示:
(1)∠ABC的角平分线;
(2)AC边上的中线;
(3)AC边上的高. 新知探究【规范解答】如图所示:
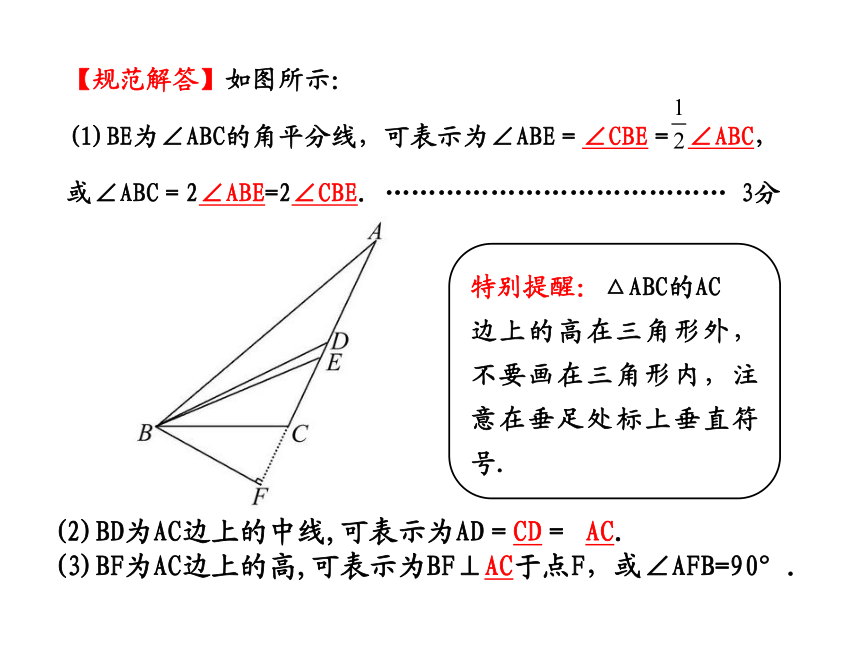
(1)BE为∠ABC的角平分线,可表示为∠ABE=∠CBE= ∠ABC,
或∠ABC=2∠ABE=2∠CBE. ………………………………… 3分特别提醒:△ABC的AC
边上的高在三角形外,不要画在三角形内,注意在垂足处标上垂直符号.(2)BD为AC边上的中线,可表示为AD=CD= AC.
(3)BF为AC边上的高,可表示为BF⊥AC于点F,或∠AFB=90°.
三角形的三种重要线段识别的两点注意
(1)不要混淆:准确把握三角形三种重要线段的概念,弄清三者的区分.
(2)注意数量关系的推理判断:三角形的角平分线可得到两个相等角,三角形的中线可得到两条相等的线段和两个面积相等的三角形,三角形的高可得到垂直关系或直角.新知探究【跟踪练习】
1.如图所示,在△ABC中,D,E,F是BC边上的三点,且∠1=∠2=∠3=∠4,AE是哪个三角形的角平分线( )
(A)△ABE (B)△ADF
(C)△ABC (D)△ABC,△ADF2.如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分
别为C,D,E,则下列说法不正确的是( )
(A)AC是△ABC的高
(B)DE是△BCD的高
(C)DE是△ABE的高
(D)AD是△ACD的高3.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
(A)锐角三角形 (B)钝角三角形
(C)直角三角形 (D)都有可能
【解析】选C.一个三角形的三条高的交点恰是三角形的一个顶点,则这个三角形是直角三角形.4、下列说法正确的是( )
①三角形的三条中线都在三角形内部;②三角形的三条角平分线都在三角形内部;③三角形三条高都在三角形的内部.
(A)①②③ (B)①②
(C)②③ (D)①③
【解析】选B.①②正确;而对于三角形的三条高:锐角三角形的三条高在三角形的内部;直角三角形有两条高在边上,一条在内部;钝角三角形有两条高在外部,一条在内部.故③错误. 三角形中三条重要线段的综合应用
【例2】已知在△ABC中,∠C>∠B,
AD是BC边上的高,AE平分∠BAC,
试说明∠DAE= (∠C-∠B).
【规范解答】因为AD⊥BC,
所以∠BDA=90°,
所以∠BAD=90°-∠B. ……………………………………… 2分新知探究【跟踪练习】
5.如图,AD,BE都是△ABC的高,则与∠CBE一定相等的角是
( )
(A)∠ABE (B)∠BAD (C)∠DAC (D)∠C
【解析】选C.在△BEC和△ADC中,∠C是公共角,∠ADC=∠BEC =90°,所以∠CBE=∠DAC.6.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=_____.
【解析】因为AE平分∠BAC,所以∠1=∠EAD+∠2,所以∠EAD=∠1-∠2=30°-20°=10°,Rt△ABD中,∠B=90°-∠BAD =90°-30°-10°=50°.
答案:50°知识梳理你有什么收获?1.把三角形的面积分为相等的两部分的是( )
(A)三角形的角平分线
(B)三角形的中线
(C)三角形的高
(D)以上都不对
【解析】选B.三角形的一条中线把三角形分成两个等底同高的三角形,所以把三角形的面积分为相等的两部分的是三角形的中线.随堂练习2.下面四个图形中,线段BE是△ABC的高的图是( )
3.如图,在△ABC中,BC边上的高是______;在△ADC中,DC边上的高是______;在△EBC中,EC边上的高是______.
【解析】△ABC是钝角三角形,BC边上的高是AD;△ADC是直角三角形,DC边上的高是直角边AD;△EBC中, EC边上的高是BG.
答案:AD AD BG4.如图,AD为△ABC的角平分线,DE∥AB交AC于点E,若∠BAC=
58°,则∠ADE=______.
【解析】因为AD为△ABC的角平分线,所以∠BAD= ∠BAC=29°.
又因为DE∥AB,所以∠ADE=∠BAD=29°.
答案:29°5.如图,△ACB中,∠ACB=90°,∠1=∠B.
(1)试说明CD是△ABC的高;
(2)如果AC=8,BC=6,AB=10,求CD的长. 【解析】(1)因为∠1+∠BCD=90°,∠1=∠B,所以
∠B+∠BCD=90°,所以∠CDB=90°,
所以△BDC是直角三角形,即CD⊥AB,故CD是△ABC的高.
(2)因为∠ACB=∠CDB=90°,
所以S△ABC = AC·BC= AB·CD.
又因为AC=8,BC=6,AB=10,
所以CD= .
有三边都相等的三角形式 三角形,也叫正三角形
2. 两边之和大于第三边。
两边之差小于第三边。
第三边大于两边之 ,小于两边之 。知识回顾三角形的三种重要线段的概念及特征 线段一点自主预习中点一点垂足高线高一点探究:三角形的三条高的关系:
如图,画出锐角三角形、直角
三角形和钝角三角形的三条高.
①锐角三角形的三条高相交于三角形___部的___个点.
②直角三角形的三条高相交于三角形的_________.
③钝角三角形的三条高所在直线相交于三角形___部的___个点.
【归纳】三角形的三条高所在的直线相交于一点.
【点拨】三角形的角平分线、高、中线都是线段.内一直角顶点外一【预习思考】
三角形的角平分线和角的平分线是一回事吗?
提示:不是.它们均平分一个角,但三角形的角平分线是一条线段,而角的平分线是一条射线. 三角形的三种重要线段区分
【例1】如图,在△ABC中,∠BCA是钝角,完成下列画图,并用适当的符号在图中表示:
(1)∠ABC的角平分线;
(2)AC边上的中线;
(3)AC边上的高. 新知探究【规范解答】如图所示:
(1)BE为∠ABC的角平分线,可表示为∠ABE=∠CBE= ∠ABC,
或∠ABC=2∠ABE=2∠CBE. ………………………………… 3分特别提醒:△ABC的AC
边上的高在三角形外,不要画在三角形内,注意在垂足处标上垂直符号.(2)BD为AC边上的中线,可表示为AD=CD= AC.
(3)BF为AC边上的高,可表示为BF⊥AC于点F,或∠AFB=90°.
三角形的三种重要线段识别的两点注意
(1)不要混淆:准确把握三角形三种重要线段的概念,弄清三者的区分.
(2)注意数量关系的推理判断:三角形的角平分线可得到两个相等角,三角形的中线可得到两条相等的线段和两个面积相等的三角形,三角形的高可得到垂直关系或直角.新知探究【跟踪练习】
1.如图所示,在△ABC中,D,E,F是BC边上的三点,且∠1=∠2=∠3=∠4,AE是哪个三角形的角平分线( )
(A)△ABE (B)△ADF
(C)△ABC (D)△ABC,△ADF2.如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分
别为C,D,E,则下列说法不正确的是( )
(A)AC是△ABC的高
(B)DE是△BCD的高
(C)DE是△ABE的高
(D)AD是△ACD的高3.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
(A)锐角三角形 (B)钝角三角形
(C)直角三角形 (D)都有可能
【解析】选C.一个三角形的三条高的交点恰是三角形的一个顶点,则这个三角形是直角三角形.4、下列说法正确的是( )
①三角形的三条中线都在三角形内部;②三角形的三条角平分线都在三角形内部;③三角形三条高都在三角形的内部.
(A)①②③ (B)①②
(C)②③ (D)①③
【解析】选B.①②正确;而对于三角形的三条高:锐角三角形的三条高在三角形的内部;直角三角形有两条高在边上,一条在内部;钝角三角形有两条高在外部,一条在内部.故③错误. 三角形中三条重要线段的综合应用
【例2】已知在△ABC中,∠C>∠B,
AD是BC边上的高,AE平分∠BAC,
试说明∠DAE= (∠C-∠B).
【规范解答】因为AD⊥BC,
所以∠BDA=90°,
所以∠BAD=90°-∠B. ……………………………………… 2分新知探究【跟踪练习】
5.如图,AD,BE都是△ABC的高,则与∠CBE一定相等的角是
( )
(A)∠ABE (B)∠BAD (C)∠DAC (D)∠C
【解析】选C.在△BEC和△ADC中,∠C是公共角,∠ADC=∠BEC =90°,所以∠CBE=∠DAC.6.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=_____.
【解析】因为AE平分∠BAC,所以∠1=∠EAD+∠2,所以∠EAD=∠1-∠2=30°-20°=10°,Rt△ABD中,∠B=90°-∠BAD =90°-30°-10°=50°.
答案:50°知识梳理你有什么收获?1.把三角形的面积分为相等的两部分的是( )
(A)三角形的角平分线
(B)三角形的中线
(C)三角形的高
(D)以上都不对
【解析】选B.三角形的一条中线把三角形分成两个等底同高的三角形,所以把三角形的面积分为相等的两部分的是三角形的中线.随堂练习2.下面四个图形中,线段BE是△ABC的高的图是( )
3.如图,在△ABC中,BC边上的高是______;在△ADC中,DC边上的高是______;在△EBC中,EC边上的高是______.
【解析】△ABC是钝角三角形,BC边上的高是AD;△ADC是直角三角形,DC边上的高是直角边AD;△EBC中, EC边上的高是BG.
答案:AD AD BG4.如图,AD为△ABC的角平分线,DE∥AB交AC于点E,若∠BAC=
58°,则∠ADE=______.
【解析】因为AD为△ABC的角平分线,所以∠BAD= ∠BAC=29°.
又因为DE∥AB,所以∠ADE=∠BAD=29°.
答案:29°5.如图,△ACB中,∠ACB=90°,∠1=∠B.
(1)试说明CD是△ABC的高;
(2)如果AC=8,BC=6,AB=10,求CD的长. 【解析】(1)因为∠1+∠BCD=90°,∠1=∠B,所以
∠B+∠BCD=90°,所以∠CDB=90°,
所以△BDC是直角三角形,即CD⊥AB,故CD是△ABC的高.
(2)因为∠ACB=∠CDB=90°,
所以S△ABC = AC·BC= AB·CD.
又因为AC=8,BC=6,AB=10,
所以CD= .
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
