4.3.1 一次函数的图象课件 (共19张PPT)
文档属性
| 名称 | 4.3.1 一次函数的图象课件 (共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 768.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-03 00:00:00 | ||
图片预览




文档简介
课件19张PPT。4.3.1一次函数的图象
————正比例函数图象复习旧知一次函数的定义: 若两个变量x,y间的关系式可以表示成
(k、b为常数,k≠0)的形式,则称
y是x是一次函数,其中x为自变量,y为因变量. 一般地,形如 y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.1、在下列函数2、函数有哪些表示方法?图象法、列表法、关系式法是一次函数的是 ,
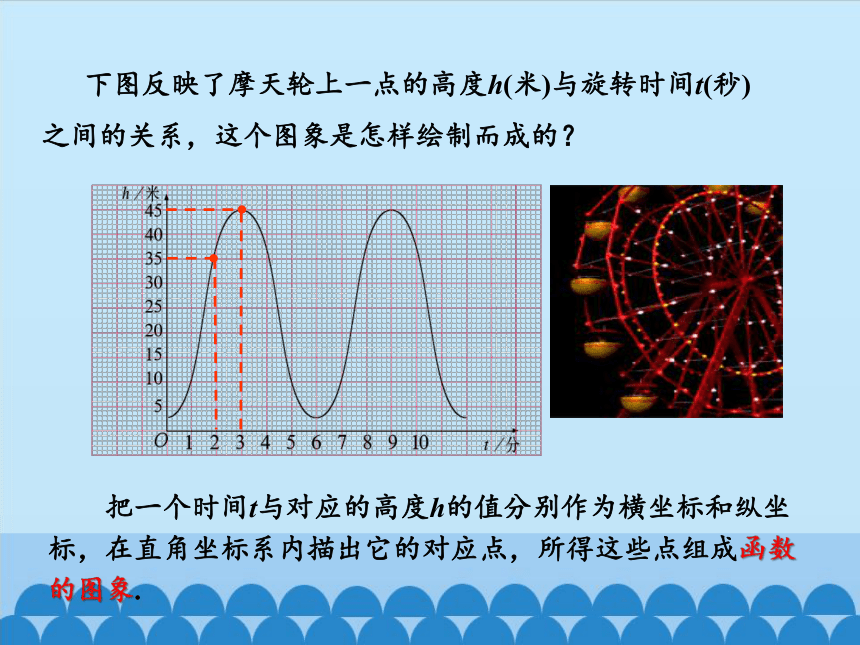
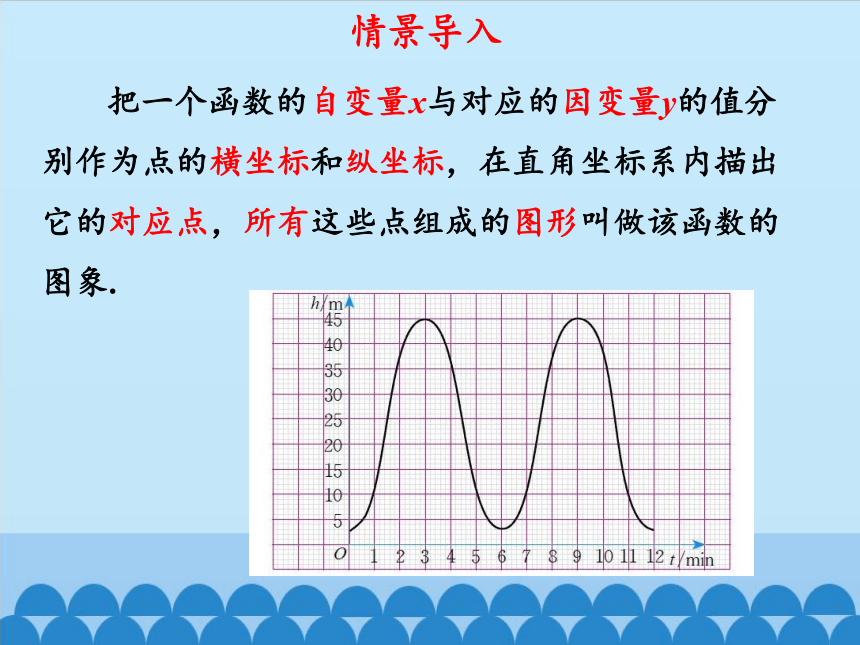
是正比例函数的是 .(2),(4)(2)三种方法可以相互转化它们之间有什么关系?3、你能将关系式法转化成图象法吗?什么是函数的图象? 下图反映了摩天轮上一点的高度h(米)与旋转时间t(秒)之间的关系,这个图象是怎样绘制而成的? 把一个时间t与对应的高度h的值分别作为横坐标和纵坐标,在直角坐标系内描出它的对应点,所得这些点组成函数的图象. 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象.情景导入画出下列正比例函数y=2x的图象.1.列表:取自变量x的一些值,计算出相应的函数值.
2.描点:建立平面直角坐标系,以自变量值为横坐标,相应的函数值为纵坐标,描出这些点.
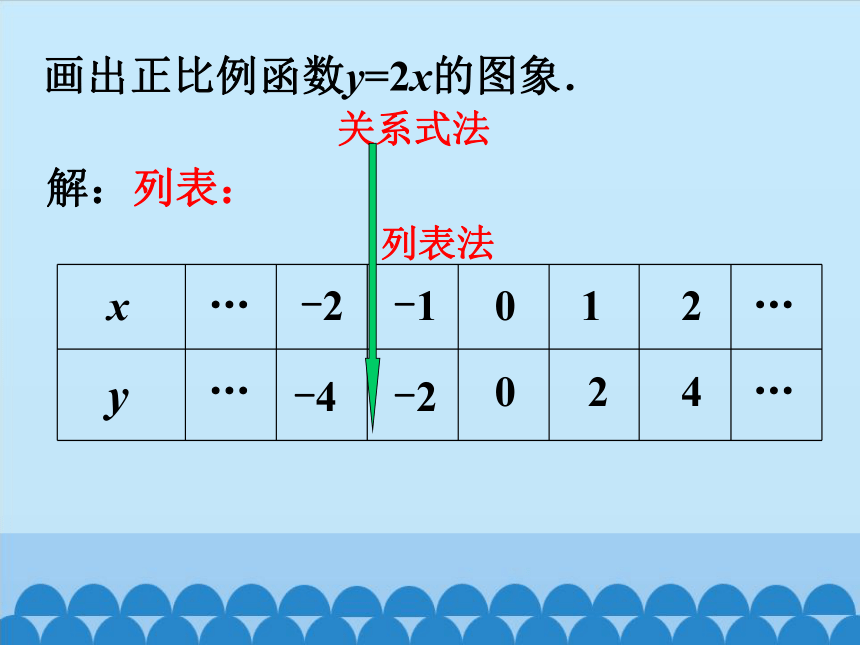
3.连线:用一条直线将平面直角坐标系中的各点连接.新知探究画出正比例函数y=2x的图象.解:列表:
xy100-12-2…………24-2-4关系式法列表法1.列表…-6-4-20246…2.描点3.连线 建立直角坐标系,以自变量为横坐标,相应的函数值为纵坐标,描出各点. 正比例函数y=2x的图象是过原点的一条直线. 正比例函数y=-3x的图象也是过原点的一条直线.画出下列正比例函数y=-3x的图象.1.列表2.描点3.连线6-303-6 正比例函数y=kx(k为常数,k≠0)的图象是过原点的一条直线.两点确定一条直线. 画正比例函数的图象时,只描出图象上的两个点,然后过两点做一条直线即可.例1 画出正比例函数y=-2x的函数. 解:当x=0时,y=0;
当x=1时,y=-2。
在平面直角坐标系中描出两点O(0,0),A(1,-2),过这两点作直线,则这条直线是y=-2x的图象。 从图中可以看出,y=2x的图象是经过原点的一条直线。例题精讲在平面直角坐标系中(如图),任意画一个正比例函数y=kx(k为常数,k≠0)的图象,它是经过原点的一条直线吗?(1)当k>0时,作y=kx的图象.观察可知y=kx(k为常数且k>0)的图象是一条经过原点的直线.
直线y=kx(k>0)经过第一、三象限且从左到右上升,y随x的增大而增大.(2)当k<0时,作y=kx的图象.观察可知y=kx(k为常数且k<0)的图象是一条经过原点的直线.
直线y=kx(k<0)经过第二、四象限且从左到右下降,y随x的增大而减小. 由于两点确定一条直线,画正比例函数图象时我们只需描点(0,0)和点 (1,k),连线即可.归 纳1.下列图象哪个可能是函数y=-8x的图象( )B 2.函数y=-5x的图象在第 象限内 ,经过点(0, )与点( 1, ), y随x的增大而_____。二,四0-5减小随堂练习 4.一次函数y=kx+b中,kb>0,且y随x的增大而减小,则它的图象大致为( ) 3.正比例函数图象y=(m-1)x的图象经过第一,三象限,则m的取值范围是( ).
A.m=1 B.m>1 C.m<1 D.m≥1 BC这节课你学到了什么知识?有什么收获?正比例函数的图象和简单性质;图象:是一条过原点的直线;性质: k>0,直线y=kx经过一,三象限从左向右上升,即y随着x的增大而增大; k<0,直线y=kx经过二,四象限从左向右下降,即y随着x的增大而减小.课堂小结谢 谢
(k、b为常数,k≠0)的形式,则称
y是x是一次函数,其中x为自变量,y为因变量. 一般地,形如 y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.1、在下列函数2、函数有哪些表示方法?图象法、列表法、关系式法是一次函数的是 ,
是正比例函数的是 .(2),(4)(2)三种方法可以相互转化它们之间有什么关系?3、你能将关系式法转化成图象法吗?什么是函数的图象? 下图反映了摩天轮上一点的高度h(米)与旋转时间t(秒)之间的关系,这个图象是怎样绘制而成的? 把一个时间t与对应的高度h的值分别作为横坐标和纵坐标,在直角坐标系内描出它的对应点,所得这些点组成函数的图象. 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象.情景导入画出下列正比例函数y=2x的图象.1.列表:取自变量x的一些值,计算出相应的函数值.
2.描点:建立平面直角坐标系,以自变量值为横坐标,相应的函数值为纵坐标,描出这些点.
3.连线:用一条直线将平面直角坐标系中的各点连接.新知探究画出正比例函数y=2x的图象.解:列表:
xy100-12-2…………24-2-4关系式法列表法1.列表…-6-4-20246…2.描点3.连线 建立直角坐标系,以自变量为横坐标,相应的函数值为纵坐标,描出各点. 正比例函数y=2x的图象是过原点的一条直线. 正比例函数y=-3x的图象也是过原点的一条直线.画出下列正比例函数y=-3x的图象.1.列表2.描点3.连线6-303-6 正比例函数y=kx(k为常数,k≠0)的图象是过原点的一条直线.两点确定一条直线. 画正比例函数的图象时,只描出图象上的两个点,然后过两点做一条直线即可.例1 画出正比例函数y=-2x的函数. 解:当x=0时,y=0;
当x=1时,y=-2。
在平面直角坐标系中描出两点O(0,0),A(1,-2),过这两点作直线,则这条直线是y=-2x的图象。 从图中可以看出,y=2x的图象是经过原点的一条直线。例题精讲在平面直角坐标系中(如图),任意画一个正比例函数y=kx(k为常数,k≠0)的图象,它是经过原点的一条直线吗?(1)当k>0时,作y=kx的图象.观察可知y=kx(k为常数且k>0)的图象是一条经过原点的直线.
直线y=kx(k>0)经过第一、三象限且从左到右上升,y随x的增大而增大.(2)当k<0时,作y=kx的图象.观察可知y=kx(k为常数且k<0)的图象是一条经过原点的直线.
直线y=kx(k<0)经过第二、四象限且从左到右下降,y随x的增大而减小. 由于两点确定一条直线,画正比例函数图象时我们只需描点(0,0)和点 (1,k),连线即可.归 纳1.下列图象哪个可能是函数y=-8x的图象( )B 2.函数y=-5x的图象在第 象限内 ,经过点(0, )与点( 1, ), y随x的增大而_____。二,四0-5减小随堂练习 4.一次函数y=kx+b中,kb>0,且y随x的增大而减小,则它的图象大致为( ) 3.正比例函数图象y=(m-1)x的图象经过第一,三象限,则m的取值范围是( ).
A.m=1 B.m>1 C.m<1 D.m≥1 BC这节课你学到了什么知识?有什么收获?正比例函数的图象和简单性质;图象:是一条过原点的直线;性质: k>0,直线y=kx经过一,三象限从左向右上升,即y随着x的增大而增大; k<0,直线y=kx经过二,四象限从左向右下降,即y随着x的增大而减小.课堂小结谢 谢
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
