2017-2018学年七年级数学北师大版下册单元测试题 第2章 相交线与平行线(原卷版+解析版)
文档属性
| 名称 | 2017-2018学年七年级数学北师大版下册单元测试题 第2章 相交线与平行线(原卷版+解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 259.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-04 00:00:00 | ||
图片预览



文档简介
《相交线与平行线》单元测试
一.选择题(共12小题)
1.如图,已知AB∥CD,∠1=115°,∠2=65°,则∠C等于( )
A.40° B.45° C.50° D.60°
2.如图所示,下列判断错误的是( )
A.若∠1=∠3,AD∥BC,则BD是∠ABC的平分线
B.若AD∥BC,则∠1=∠2=∠3
C.若∠3+∠4+∠C=180°,则AD∥BC
D.若∠2=∠3,则AD∥BC
3.如图,下列判断错误的是( )
A.∵∠1=∠2,∴AE∥BD B.∵∠3=∠4,∴AB∥CD
C.∵∠1=∠2,∴AB∥DE D.∵∠5=∠BDC,∴AE∥BD
4.如图,已知直线AB,CD被直线EF所截,如果AB∥CD,那么( )
A.∠1>∠2 B.∠1=∠2 C.∠1<∠2 D.∠1+∠2=180°
5.下列作图语句的叙述正确的是( )
A.以点O为圆心画弧 B.以AB、CD的长为半径画弧
C.延长线段BC到点D,使CD=BC D.延长线段BC=a
6.有下列说法:
①两条直线相交成四个角,如果两个角相等,那么这两条直线垂直;
②两条直线相交成四个角,如果三个角相等,那么这两条直线垂直;
③在同一平面内,过直线上一点可以作无数条直线与已知直线垂直;
④直线外一点到这条的垂线段,叫做点到直线的距离.
其中正确的说法有( )
A.0个 B.1个 C.2个 D.3个
7.由图可知,∠1和∠2是一对( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
8.如图,AB⊥AC于A,AD⊥BC于D,DE⊥AC于E,下列说法错误的是( )
A.点A到BC的距离是AD的长度 B.点B到AD的距离是BD的长度
C.点C到AD的距离是DE的长度 D.点B到AC的距离是AB的长度
9.如果直线MN外一点A到直线MN的距离是3cm,那么点A与直线MN上任意一点B所连成的线段AB的长度一定是( )
A.3cm B.小于3cm
C.大于3cm D.大于或等于3cm
10.下列作图属于尺规作图的是( )
A.用量角器画出∠AOB的平分线OC
B.作∠AOB,使∠AOB=2α
C.画线段AB=3厘米
D.用三角板过点P作AB的垂线
11.4条直线交于一点,则对顶角有( )
A.4对 B.6对 C.8对 D.12对
12.已知n(n≥3,且n为整数)条直线中只有两条直线平行,且任何三条直线都不交于同一个点.如图,当n=3时,共有2个交点;当n=4时,共有5个交点;当n=5时,共有9个交点;…依此规律,当共有交点个数为27时,则n的值为( )
A.6 B.7 C.8 D.9
二.填空题(共4小题)
13.如图所示,如果BD平分∠ABC,补上一个条件 作为已知,就能推出AB∥CD.
14.如图,直线AB和CD相交于点O,若∠AOD=5∠AOC,则∠BOC= .
15.如图所示,A、B之间是一座山,一条铁路要过A、B两县,在A地测得铁路走向是北偏东64°,那么B地按南偏西的 °方向施工,才能使铁路在山腰中准确接通.
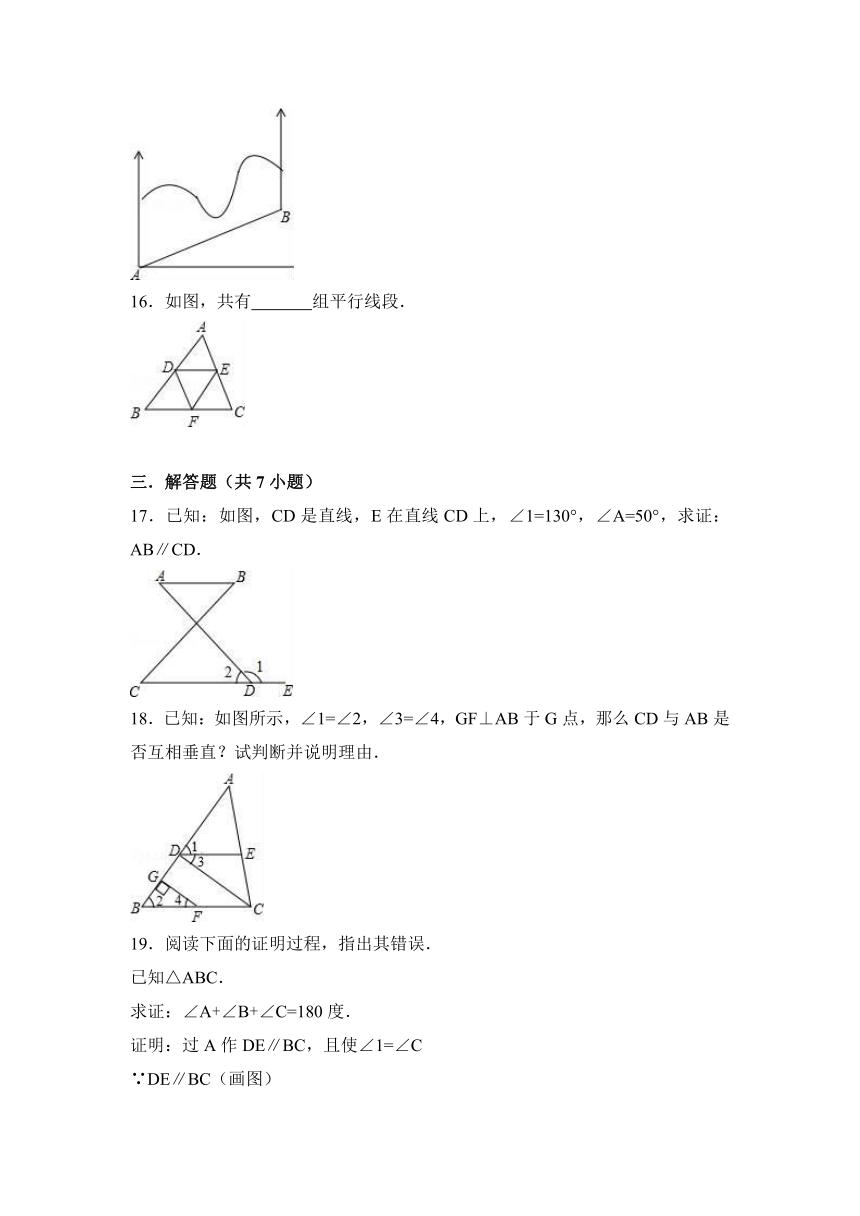
16.如图,共有 组平行线段.
三.解答题(共7小题)
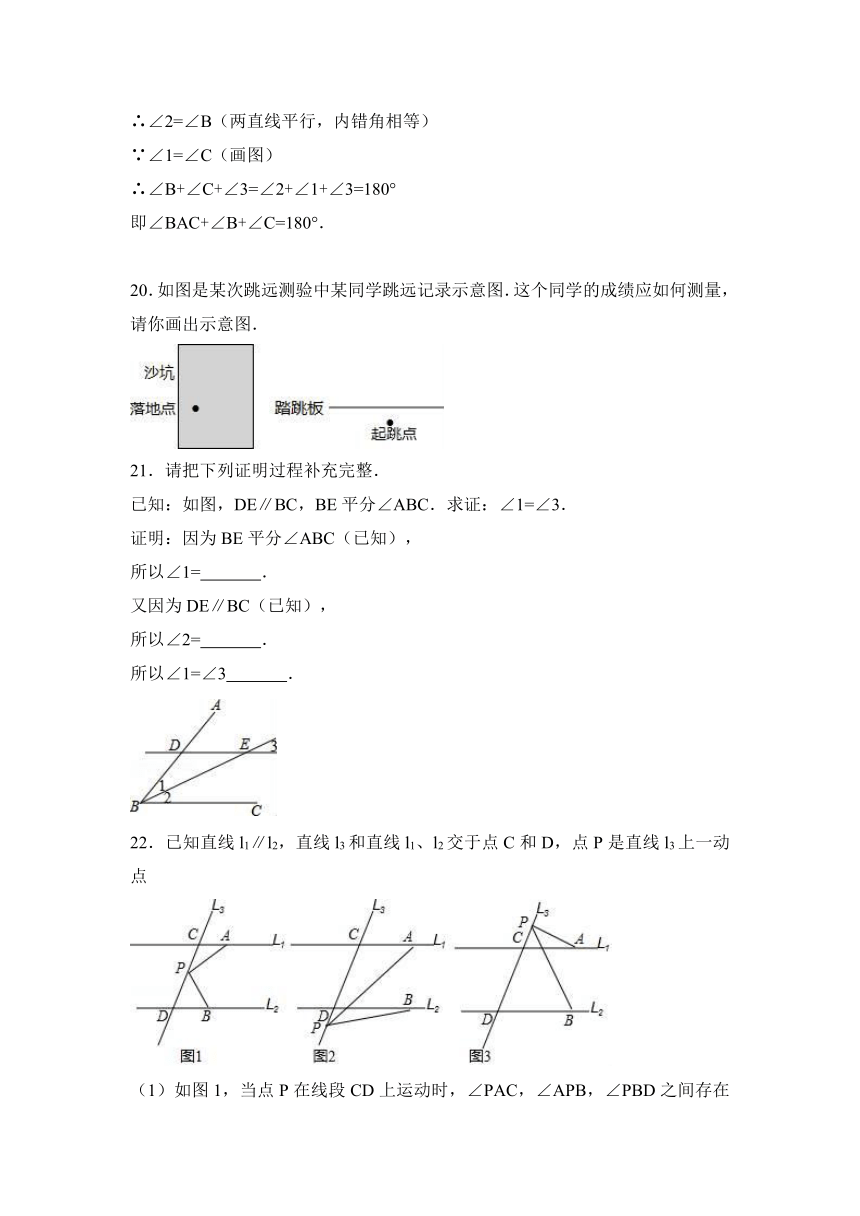
17.已知:如图,CD是直线,E在直线CD上,∠1=130°,∠A=50°,求证:AB∥CD.
18.已知:如图所示,∠1=∠2,∠3=∠4,GF⊥AB于G点,那么CD与AB是否互相垂直?试判断并说明理由.
19.阅读下面的证明过程,指出其错误.
已知△ABC.
求证:∠A+∠B+∠C=180度.
证明:过A作DE∥BC,且使∠1=∠C
∵DE∥BC(画图)
∴∠2=∠B(两直线平行,内错角相等)
∵∠1=∠C(画图)
∴∠B+∠C+∠3=∠2+∠1+∠3=180°
即∠BAC+∠B+∠C=180°.
20.如图是某次跳远测验中某同学跳远记录示意图.这个同学的成绩应如何测量,请你画出示意图.
21.请把下列证明过程补充完整.
已知:如图,DE∥BC,BE平分∠ABC.求证:∠1=∠3.
证明:因为BE平分∠ABC(已知),
所以∠1= .
又因为DE∥BC(已知),
所以∠2= .
所以∠1=∠3 .
22.已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
23.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点.
(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.
参考答案与试题解析
一.选择题(共12小题)
1.如图,已知AB∥CD,∠1=115°,∠2=65°,则∠C等于( )
A.40° B.45° C.50° D.60°
【解答】解:∵AB∥CD,
∴∠1=∠EGD=115°,
∵∠2=65°,
∴∠C=115°﹣65°=50°,
故选:C.
2.如图所示,下列判断错误的是( )
A.若∠1=∠3,AD∥BC,则BD是∠ABC的平分线
B.若AD∥BC,则∠1=∠2=∠3
C.若∠3+∠4+∠C=180°,则AD∥BC
D.若∠2=∠3,则AD∥BC
【解答】解:A、∵AD∥BC,
∴∠2=∠3,
又∵∠1=∠3,
∴∠1=∠2,则BD是∠ABC的平分线;
B、∠2,∠3是直线AD和直线BC被直线BD所截形成的内错角,若AD∥BC,则∠2=∠3,∠1是直线AB和直线AD被直线BD所截形成的角,因此,若AD∥BC,不能证明∠1=∠2=∠3;
C、∠3+∠4+∠C=180°,即同旁内角∠ADC+∠C=180°,则AD∥BC;
D、内错角∠2=∠3,则AD∥BC.
故选:B.
3.如图,下列判断错误的是( )
A.∵∠1=∠2,∴AE∥BD B.∵∠3=∠4,∴AB∥CD
C.∵∠1=∠2,∴AB∥DE D.∵∠5=∠BDC,∴AE∥BD
【解答】解:A、∵∠1=∠2,
∴AE∥BD(内错角相等,两直线平行),故此选项不合题意;
B、∵∠3=∠4,
∴AB∥CD(内错角相等,两直线平行),故此选项不合题意;
C、∵∠1=∠2,
∴AB∥DE错误,应该是AE∥BD,故此选项符合题意;
D、∵∠5=∠BDC,
∴AE∥BD(同位角相等,两直线平行),故此选项不合题意;
故选:C.
4.如图,已知直线AB,CD被直线EF所截,如果AB∥CD,那么( )
A.∠1>∠2 B.∠1=∠2 C.∠1<∠2 D.∠1+∠2=180°
【解答】解:如图,∵AB∥CD,
∴∠2=∠3,
∵∠1=∠3,
∴∠1=∠2.
故选:B.
5.下列作图语句的叙述正确的是( )
A.以点O为圆心画弧 B.以AB、CD的长为半径画弧
C.延长线段BC到点D,使CD=BC D.延长线段BC=a
【解答】解:A、以点O为圆心画弧,画弧应有半径,故此选项错误;
B、以AB、CD的长为半径画弧,应有圆心,故此选项错误;
C、延长线段BC到点D,使CD=BC,此选项正确;
D、延长线段BC=a,应等于具体长度,故此选项错误.
故选:C.
6.有下列说法:
①两条直线相交成四个角,如果两个角相等,那么这两条直线垂直;
②两条直线相交成四个角,如果三个角相等,那么这两条直线垂直;
③在同一平面内,过直线上一点可以作无数条直线与已知直线垂直;
④直线外一点到这条的垂线段,叫做点到直线的距离.
其中正确的说法有( )
A.0个 B.1个 C.2个 D.3个
【解答】解:①两条直线相交成四个角,如果有一对对顶角相等且均不为90°,那么这两条直线不垂直,故①错误;
②两条直线相交成四个角,则这四个角中有2对对顶角.如果三个角相等,则这四个角相等,都是直角,所以这两条直线垂直.故②正确;
③在同一平面内,过直线上一点只有一条直线与已知直线垂直.故③错误;
④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.故④错误;
综上所述,正确的说法是1个.
故选:B.
7.由图可知,∠1和∠2是一对( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
【解答】解:∠1与∠2符合内错角定义.
故选:C.
8.如图,AB⊥AC于A,AD⊥BC于D,DE⊥AC于E,下列说法错误的是( )
A.点A到BC的距离是AD的长度 B.点B到AD的距离是BD的长度
C.点C到AD的距离是DE的长度 D.点B到AC的距离是AB的长度
【解答】解:A、点A到BC的距离是AD的长度,本选项正确,不符合题意;
B、点B到AD的距离是BD的长度,本选项正确,不符合题意;
C、点C到AD的距离是CD的长度,故本选项错误,符合题意;
D、点B到AC的距离是AB的长度,本选项正确,不符合题意.
故选:C.
9.如果直线MN外一点A到直线MN的距离是3cm,那么点A与直线MN上任意一点B所连成的线段AB的长度一定是( )
A.3cm B.小于3cm
C.大于3cm D.大于或等于3cm
【解答】解:A到直线MN的距离是3cm,根据点到直线距离的定义,3cm表示垂线段的长度,根据垂线段最短,其它线段的长度大于或等于3cm,故选D.
10.下列作图属于尺规作图的是( )
A.用量角器画出∠AOB的平分线OC
B.作∠AOB,使∠AOB=2α
C.画线段AB=3厘米
D.用三角板过点P作AB的垂线
【解答】解:根据尺规作图的定义可得:B属于尺规作图,
故选:B.
11.4条直线交于一点,则对顶角有( )
A.4对 B.6对 C.8对 D.12对
【解答】解:根据对顶角的定义可知:4条直线交于一点,则对顶角有12对.故选D.
12.已知n(n≥3,且n为整数)条直线中只有两条直线平行,且任何三条直线都不交于同一个点.如图,当n=3时,共有2个交点;当n=4时,共有5个交点;当n=5时,共有9个交点;…依此规律,当共有交点个数为27时,则n的值为( )
A.6 B.7 C.8 D.9
【解答】解:∵当n≥3时,每增加一条直线,交点的个数就增加n﹣1.即:
当n=3时,共有2个交点;
当n=4时,共有5(=2+3)个交点;
当n=5时,共有9(=5+4)个交点;
…,
∴n条直线共有交点2+3+4+…+(n﹣1)=个.
解方程=27,得n=8或﹣7(负值舍去).
故选:C.
二.填空题(共4小题)
13.如图所示,如果BD平分∠ABC,补上一个条件 ∠2=∠3,或DC=BC 作为已知,就能推出AB∥CD.
【解答】解:可添加∠2=∠3;
∵BD平分∠ABC,∴∠1=∠2,
若∠2=∠3,∴可得∠1=∠3,
∴AB∥CD.
14.如图,直线AB和CD相交于点O,若∠AOD=5∠AOC,则∠BOC= 150° .
【解答】解:∵∠AOD+∠AOC=180°,
∠AOD=5∠AOC,
∴5∠AOC+∠AOC=180°,
∴∠AOC=30°,
∴∠AOD=5×30°=150°,
∴∠BOC=∠AOD=150°,
故答案为:150°.
15.如图所示,A、B之间是一座山,一条铁路要过A、B两县,在A地测得铁路走向是北偏东64°,那么B地按南偏西的 64 °方向施工,才能使铁路在山腰中准确接通.
【解答】解:由于是相向开工.故角度相等,方向相反.
而∠ABE和∠BAC为同位角,
于是∠ABE=∠BAC=64°,
故答案为64°.
16.如图,共有 9 组平行线段.
【解答】解:图中的平行线段有AD∥EF;BD∥EF;DE∥FB;DE∥FC;DF∥AE;DF∥EC;DE∥BC;DF∥AC;EF∥AB.共有9对.
故答案为:9.
三.解答题(共7小题)
17.已知:如图,CD是直线,E在直线CD上,∠1=130°,∠A=50°,求证:AB∥CD.
【解答】证明:∵∠1+∠2=180°,∠1=130°,
∴∠2=50°,
∵∠A=50°,
∴∠A=∠2,
∴AB∥CD.
18.已知:如图所示,∠1=∠2,∠3=∠4,GF⊥AB于G点,那么CD与AB是否互相垂直?试判断并说明理由.
【解答】解:相互垂直.
理由:∵GF⊥AB,
∴∠2+∠4=90°,
而∠1=∠2,∠3=∠4,
∴∠1+∠3=90°,
∴CD⊥AB.
19.阅读下面的证明过程,指出其错误.
已知△ABC.
求证:∠A+∠B+∠C=180度.
证明:过A作DE∥BC,且使∠1=∠C
∵DE∥BC(画图)
∴∠2=∠B(两直线平行,内错角相等)
∵∠1=∠C(画图)
∴∠B+∠C+∠3=∠2+∠1+∠3=180°
即∠BAC+∠B+∠C=180°.
【解答】解:错误:过A作DE∥BC,且使∠1=∠C,应改为:过A作DE∥BC.∵∠1=∠C(画图),应改为∴∠1=∠C(两直线平行,内错角相等).
证明:过A作DE∥BC,
∵DE∥BC(画图),
∴∠2=∠B,∠1=∠C(两直线平行,内错角相等),
∴∠B+∠C+∠3=∠2+∠1+∠3=180°,
即∠BAC+∠B+∠C=180°.
20.如图是某次跳远测验中某同学跳远记录示意图.这个同学的成绩应如何测量,请你画出示意图.
【解答】解:如图所示,红线的长度即为该同学的跳远成绩.
21.请把下列证明过程补充完整.
已知:如图,DE∥BC,BE平分∠ABC.求证:∠1=∠3.
证明:因为BE平分∠ABC(已知),
所以∠1= ∠2 .
又因为DE∥BC(已知),
所以∠2= ∠DEB .
所以∠1=∠3 (等量代换) .
【解答】证明:∵BE平分∠ABC,
∴∠1=∠2,
∵DE∥BC,
∴∠2=∠DEB,
∴∠1=∠DEB,
∵∠3=∠DEB,
∴∠1=∠3(等量代换),
故答案为:∠2,∠DEB,(等量代换)
22.已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
【解答】解:(1)∠APB=∠PAC+∠PBD,
如图1,过点P作PE∥l1,
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∴∠APE+∠BPE=∠PAC+∠PBD,
∴∠APB=∠PAC+∠PBD;
(2)不成立,
如图2:∠PAC=∠APB+∠PBD,
理由:过点P作PE∥l1,
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∵∠APB=∠APE﹣∠BPE=∠PAC﹣∠PBD,
∴∠PAC=∠APB+∠PBD;
如图3:∠PBD=∠PAC+∠APB,
理由:过点P作PE∥l1,
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∵APB=∠BPE﹣∠APE=∠PBD﹣∠PAC,
∴∠PBD=∠PAC+∠APB.
23.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点.
(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.
【解答】解:(1)如图1,作MQ∥AB,,
∵AB∥CD,MQ∥AB,
∴MQ∥CD,
∴∠1=∠FHM,∠2=∠DEM,
∴∠1+∠2=∠FHM+∠DEM=(∠FHP+∠FED)=(∠FHP+∠HFP),
∵HP⊥EF,
∴∠HPF=90°,
∴∠FHP+∠HFP=180°﹣90°=90°,
∵∠1+∠2=∠M,
∴∠M=.
(2)①如图2,,
∠FHE=2∠ENQ,理由如下:
∠NEQ=∠NEF+∠QEF=(∠HEF+∠DEF)=∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=(180°﹣∠HED)=∠CEH,
∵AB∥CD,
∴∠FHE=∠CEH=2∠ENQ.
②如图3,,
∠FHE=180°﹣2∠ENQ,理由如下:
∠NEQ=∠QEF﹣∠NEF=(∠DEF﹣∠HEF)=∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=(180°﹣∠HED)=∠CEH,
∵AB∥CD,
∴∠FHE=180°﹣∠CEH=180°﹣2∠ENQ.
综上,可得
当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或∠FHE=180°﹣2∠ENQ.
一.选择题(共12小题)
1.如图,已知AB∥CD,∠1=115°,∠2=65°,则∠C等于( )
A.40° B.45° C.50° D.60°
2.如图所示,下列判断错误的是( )
A.若∠1=∠3,AD∥BC,则BD是∠ABC的平分线
B.若AD∥BC,则∠1=∠2=∠3
C.若∠3+∠4+∠C=180°,则AD∥BC
D.若∠2=∠3,则AD∥BC
3.如图,下列判断错误的是( )
A.∵∠1=∠2,∴AE∥BD B.∵∠3=∠4,∴AB∥CD
C.∵∠1=∠2,∴AB∥DE D.∵∠5=∠BDC,∴AE∥BD
4.如图,已知直线AB,CD被直线EF所截,如果AB∥CD,那么( )
A.∠1>∠2 B.∠1=∠2 C.∠1<∠2 D.∠1+∠2=180°
5.下列作图语句的叙述正确的是( )
A.以点O为圆心画弧 B.以AB、CD的长为半径画弧
C.延长线段BC到点D,使CD=BC D.延长线段BC=a
6.有下列说法:
①两条直线相交成四个角,如果两个角相等,那么这两条直线垂直;
②两条直线相交成四个角,如果三个角相等,那么这两条直线垂直;
③在同一平面内,过直线上一点可以作无数条直线与已知直线垂直;
④直线外一点到这条的垂线段,叫做点到直线的距离.
其中正确的说法有( )
A.0个 B.1个 C.2个 D.3个
7.由图可知,∠1和∠2是一对( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
8.如图,AB⊥AC于A,AD⊥BC于D,DE⊥AC于E,下列说法错误的是( )
A.点A到BC的距离是AD的长度 B.点B到AD的距离是BD的长度
C.点C到AD的距离是DE的长度 D.点B到AC的距离是AB的长度
9.如果直线MN外一点A到直线MN的距离是3cm,那么点A与直线MN上任意一点B所连成的线段AB的长度一定是( )
A.3cm B.小于3cm
C.大于3cm D.大于或等于3cm
10.下列作图属于尺规作图的是( )
A.用量角器画出∠AOB的平分线OC
B.作∠AOB,使∠AOB=2α
C.画线段AB=3厘米
D.用三角板过点P作AB的垂线
11.4条直线交于一点,则对顶角有( )
A.4对 B.6对 C.8对 D.12对
12.已知n(n≥3,且n为整数)条直线中只有两条直线平行,且任何三条直线都不交于同一个点.如图,当n=3时,共有2个交点;当n=4时,共有5个交点;当n=5时,共有9个交点;…依此规律,当共有交点个数为27时,则n的值为( )
A.6 B.7 C.8 D.9
二.填空题(共4小题)
13.如图所示,如果BD平分∠ABC,补上一个条件 作为已知,就能推出AB∥CD.
14.如图,直线AB和CD相交于点O,若∠AOD=5∠AOC,则∠BOC= .
15.如图所示,A、B之间是一座山,一条铁路要过A、B两县,在A地测得铁路走向是北偏东64°,那么B地按南偏西的 °方向施工,才能使铁路在山腰中准确接通.
16.如图,共有 组平行线段.
三.解答题(共7小题)
17.已知:如图,CD是直线,E在直线CD上,∠1=130°,∠A=50°,求证:AB∥CD.
18.已知:如图所示,∠1=∠2,∠3=∠4,GF⊥AB于G点,那么CD与AB是否互相垂直?试判断并说明理由.
19.阅读下面的证明过程,指出其错误.
已知△ABC.
求证:∠A+∠B+∠C=180度.
证明:过A作DE∥BC,且使∠1=∠C
∵DE∥BC(画图)
∴∠2=∠B(两直线平行,内错角相等)
∵∠1=∠C(画图)
∴∠B+∠C+∠3=∠2+∠1+∠3=180°
即∠BAC+∠B+∠C=180°.
20.如图是某次跳远测验中某同学跳远记录示意图.这个同学的成绩应如何测量,请你画出示意图.
21.请把下列证明过程补充完整.
已知:如图,DE∥BC,BE平分∠ABC.求证:∠1=∠3.
证明:因为BE平分∠ABC(已知),
所以∠1= .
又因为DE∥BC(已知),
所以∠2= .
所以∠1=∠3 .
22.已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
23.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点.
(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.
参考答案与试题解析
一.选择题(共12小题)
1.如图,已知AB∥CD,∠1=115°,∠2=65°,则∠C等于( )
A.40° B.45° C.50° D.60°
【解答】解:∵AB∥CD,
∴∠1=∠EGD=115°,
∵∠2=65°,
∴∠C=115°﹣65°=50°,
故选:C.
2.如图所示,下列判断错误的是( )
A.若∠1=∠3,AD∥BC,则BD是∠ABC的平分线
B.若AD∥BC,则∠1=∠2=∠3
C.若∠3+∠4+∠C=180°,则AD∥BC
D.若∠2=∠3,则AD∥BC
【解答】解:A、∵AD∥BC,
∴∠2=∠3,
又∵∠1=∠3,
∴∠1=∠2,则BD是∠ABC的平分线;
B、∠2,∠3是直线AD和直线BC被直线BD所截形成的内错角,若AD∥BC,则∠2=∠3,∠1是直线AB和直线AD被直线BD所截形成的角,因此,若AD∥BC,不能证明∠1=∠2=∠3;
C、∠3+∠4+∠C=180°,即同旁内角∠ADC+∠C=180°,则AD∥BC;
D、内错角∠2=∠3,则AD∥BC.
故选:B.
3.如图,下列判断错误的是( )
A.∵∠1=∠2,∴AE∥BD B.∵∠3=∠4,∴AB∥CD
C.∵∠1=∠2,∴AB∥DE D.∵∠5=∠BDC,∴AE∥BD
【解答】解:A、∵∠1=∠2,
∴AE∥BD(内错角相等,两直线平行),故此选项不合题意;
B、∵∠3=∠4,
∴AB∥CD(内错角相等,两直线平行),故此选项不合题意;
C、∵∠1=∠2,
∴AB∥DE错误,应该是AE∥BD,故此选项符合题意;
D、∵∠5=∠BDC,
∴AE∥BD(同位角相等,两直线平行),故此选项不合题意;
故选:C.
4.如图,已知直线AB,CD被直线EF所截,如果AB∥CD,那么( )
A.∠1>∠2 B.∠1=∠2 C.∠1<∠2 D.∠1+∠2=180°
【解答】解:如图,∵AB∥CD,
∴∠2=∠3,
∵∠1=∠3,
∴∠1=∠2.
故选:B.
5.下列作图语句的叙述正确的是( )
A.以点O为圆心画弧 B.以AB、CD的长为半径画弧
C.延长线段BC到点D,使CD=BC D.延长线段BC=a
【解答】解:A、以点O为圆心画弧,画弧应有半径,故此选项错误;
B、以AB、CD的长为半径画弧,应有圆心,故此选项错误;
C、延长线段BC到点D,使CD=BC,此选项正确;
D、延长线段BC=a,应等于具体长度,故此选项错误.
故选:C.
6.有下列说法:
①两条直线相交成四个角,如果两个角相等,那么这两条直线垂直;
②两条直线相交成四个角,如果三个角相等,那么这两条直线垂直;
③在同一平面内,过直线上一点可以作无数条直线与已知直线垂直;
④直线外一点到这条的垂线段,叫做点到直线的距离.
其中正确的说法有( )
A.0个 B.1个 C.2个 D.3个
【解答】解:①两条直线相交成四个角,如果有一对对顶角相等且均不为90°,那么这两条直线不垂直,故①错误;
②两条直线相交成四个角,则这四个角中有2对对顶角.如果三个角相等,则这四个角相等,都是直角,所以这两条直线垂直.故②正确;
③在同一平面内,过直线上一点只有一条直线与已知直线垂直.故③错误;
④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.故④错误;
综上所述,正确的说法是1个.
故选:B.
7.由图可知,∠1和∠2是一对( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
【解答】解:∠1与∠2符合内错角定义.
故选:C.
8.如图,AB⊥AC于A,AD⊥BC于D,DE⊥AC于E,下列说法错误的是( )
A.点A到BC的距离是AD的长度 B.点B到AD的距离是BD的长度
C.点C到AD的距离是DE的长度 D.点B到AC的距离是AB的长度
【解答】解:A、点A到BC的距离是AD的长度,本选项正确,不符合题意;
B、点B到AD的距离是BD的长度,本选项正确,不符合题意;
C、点C到AD的距离是CD的长度,故本选项错误,符合题意;
D、点B到AC的距离是AB的长度,本选项正确,不符合题意.
故选:C.
9.如果直线MN外一点A到直线MN的距离是3cm,那么点A与直线MN上任意一点B所连成的线段AB的长度一定是( )
A.3cm B.小于3cm
C.大于3cm D.大于或等于3cm
【解答】解:A到直线MN的距离是3cm,根据点到直线距离的定义,3cm表示垂线段的长度,根据垂线段最短,其它线段的长度大于或等于3cm,故选D.
10.下列作图属于尺规作图的是( )
A.用量角器画出∠AOB的平分线OC
B.作∠AOB,使∠AOB=2α
C.画线段AB=3厘米
D.用三角板过点P作AB的垂线
【解答】解:根据尺规作图的定义可得:B属于尺规作图,
故选:B.
11.4条直线交于一点,则对顶角有( )
A.4对 B.6对 C.8对 D.12对
【解答】解:根据对顶角的定义可知:4条直线交于一点,则对顶角有12对.故选D.
12.已知n(n≥3,且n为整数)条直线中只有两条直线平行,且任何三条直线都不交于同一个点.如图,当n=3时,共有2个交点;当n=4时,共有5个交点;当n=5时,共有9个交点;…依此规律,当共有交点个数为27时,则n的值为( )
A.6 B.7 C.8 D.9
【解答】解:∵当n≥3时,每增加一条直线,交点的个数就增加n﹣1.即:
当n=3时,共有2个交点;
当n=4时,共有5(=2+3)个交点;
当n=5时,共有9(=5+4)个交点;
…,
∴n条直线共有交点2+3+4+…+(n﹣1)=个.
解方程=27,得n=8或﹣7(负值舍去).
故选:C.
二.填空题(共4小题)
13.如图所示,如果BD平分∠ABC,补上一个条件 ∠2=∠3,或DC=BC 作为已知,就能推出AB∥CD.
【解答】解:可添加∠2=∠3;
∵BD平分∠ABC,∴∠1=∠2,
若∠2=∠3,∴可得∠1=∠3,
∴AB∥CD.
14.如图,直线AB和CD相交于点O,若∠AOD=5∠AOC,则∠BOC= 150° .
【解答】解:∵∠AOD+∠AOC=180°,
∠AOD=5∠AOC,
∴5∠AOC+∠AOC=180°,
∴∠AOC=30°,
∴∠AOD=5×30°=150°,
∴∠BOC=∠AOD=150°,
故答案为:150°.
15.如图所示,A、B之间是一座山,一条铁路要过A、B两县,在A地测得铁路走向是北偏东64°,那么B地按南偏西的 64 °方向施工,才能使铁路在山腰中准确接通.
【解答】解:由于是相向开工.故角度相等,方向相反.
而∠ABE和∠BAC为同位角,
于是∠ABE=∠BAC=64°,
故答案为64°.
16.如图,共有 9 组平行线段.
【解答】解:图中的平行线段有AD∥EF;BD∥EF;DE∥FB;DE∥FC;DF∥AE;DF∥EC;DE∥BC;DF∥AC;EF∥AB.共有9对.
故答案为:9.
三.解答题(共7小题)
17.已知:如图,CD是直线,E在直线CD上,∠1=130°,∠A=50°,求证:AB∥CD.
【解答】证明:∵∠1+∠2=180°,∠1=130°,
∴∠2=50°,
∵∠A=50°,
∴∠A=∠2,
∴AB∥CD.
18.已知:如图所示,∠1=∠2,∠3=∠4,GF⊥AB于G点,那么CD与AB是否互相垂直?试判断并说明理由.
【解答】解:相互垂直.
理由:∵GF⊥AB,
∴∠2+∠4=90°,
而∠1=∠2,∠3=∠4,
∴∠1+∠3=90°,
∴CD⊥AB.
19.阅读下面的证明过程,指出其错误.
已知△ABC.
求证:∠A+∠B+∠C=180度.
证明:过A作DE∥BC,且使∠1=∠C
∵DE∥BC(画图)
∴∠2=∠B(两直线平行,内错角相等)
∵∠1=∠C(画图)
∴∠B+∠C+∠3=∠2+∠1+∠3=180°
即∠BAC+∠B+∠C=180°.
【解答】解:错误:过A作DE∥BC,且使∠1=∠C,应改为:过A作DE∥BC.∵∠1=∠C(画图),应改为∴∠1=∠C(两直线平行,内错角相等).
证明:过A作DE∥BC,
∵DE∥BC(画图),
∴∠2=∠B,∠1=∠C(两直线平行,内错角相等),
∴∠B+∠C+∠3=∠2+∠1+∠3=180°,
即∠BAC+∠B+∠C=180°.
20.如图是某次跳远测验中某同学跳远记录示意图.这个同学的成绩应如何测量,请你画出示意图.
【解答】解:如图所示,红线的长度即为该同学的跳远成绩.
21.请把下列证明过程补充完整.
已知:如图,DE∥BC,BE平分∠ABC.求证:∠1=∠3.
证明:因为BE平分∠ABC(已知),
所以∠1= ∠2 .
又因为DE∥BC(已知),
所以∠2= ∠DEB .
所以∠1=∠3 (等量代换) .
【解答】证明:∵BE平分∠ABC,
∴∠1=∠2,
∵DE∥BC,
∴∠2=∠DEB,
∴∠1=∠DEB,
∵∠3=∠DEB,
∴∠1=∠3(等量代换),
故答案为:∠2,∠DEB,(等量代换)
22.已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
【解答】解:(1)∠APB=∠PAC+∠PBD,
如图1,过点P作PE∥l1,
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∴∠APE+∠BPE=∠PAC+∠PBD,
∴∠APB=∠PAC+∠PBD;
(2)不成立,
如图2:∠PAC=∠APB+∠PBD,
理由:过点P作PE∥l1,
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∵∠APB=∠APE﹣∠BPE=∠PAC﹣∠PBD,
∴∠PAC=∠APB+∠PBD;
如图3:∠PBD=∠PAC+∠APB,
理由:过点P作PE∥l1,
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∵APB=∠BPE﹣∠APE=∠PBD﹣∠PAC,
∴∠PBD=∠PAC+∠APB.
23.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点.
(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.
【解答】解:(1)如图1,作MQ∥AB,,
∵AB∥CD,MQ∥AB,
∴MQ∥CD,
∴∠1=∠FHM,∠2=∠DEM,
∴∠1+∠2=∠FHM+∠DEM=(∠FHP+∠FED)=(∠FHP+∠HFP),
∵HP⊥EF,
∴∠HPF=90°,
∴∠FHP+∠HFP=180°﹣90°=90°,
∵∠1+∠2=∠M,
∴∠M=.
(2)①如图2,,
∠FHE=2∠ENQ,理由如下:
∠NEQ=∠NEF+∠QEF=(∠HEF+∠DEF)=∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=(180°﹣∠HED)=∠CEH,
∵AB∥CD,
∴∠FHE=∠CEH=2∠ENQ.
②如图3,,
∠FHE=180°﹣2∠ENQ,理由如下:
∠NEQ=∠QEF﹣∠NEF=(∠DEF﹣∠HEF)=∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=(180°﹣∠HED)=∠CEH,
∵AB∥CD,
∴∠FHE=180°﹣∠CEH=180°﹣2∠ENQ.
综上,可得
当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或∠FHE=180°﹣2∠ENQ.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
