人教版八年级下册18.2.2菱形的判定定理公开课课件(共21张PPT)
文档属性
| 名称 | 人教版八年级下册18.2.2菱形的判定定理公开课课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 379.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-04 00:00:00 | ||
图片预览





文档简介
课件21张PPT。 汶川地震后,全国各界组织发起“绿丝带行动”,号召人民为四川受灾的人们祈福。人们将绿丝带剪成小段,并用别针将折叠好的绿丝带别在胸前,如图所示,绿丝带重叠部分形成的图形是一个漂亮的菱形。你知道是怎样判断它是一个菱形的吗?初中数学八年级下册
菱形的判定学习目标:
1.探究并证明菱形判定定理,体会类比思想和转化的数学思想,了解研究图形判定的一般思路.
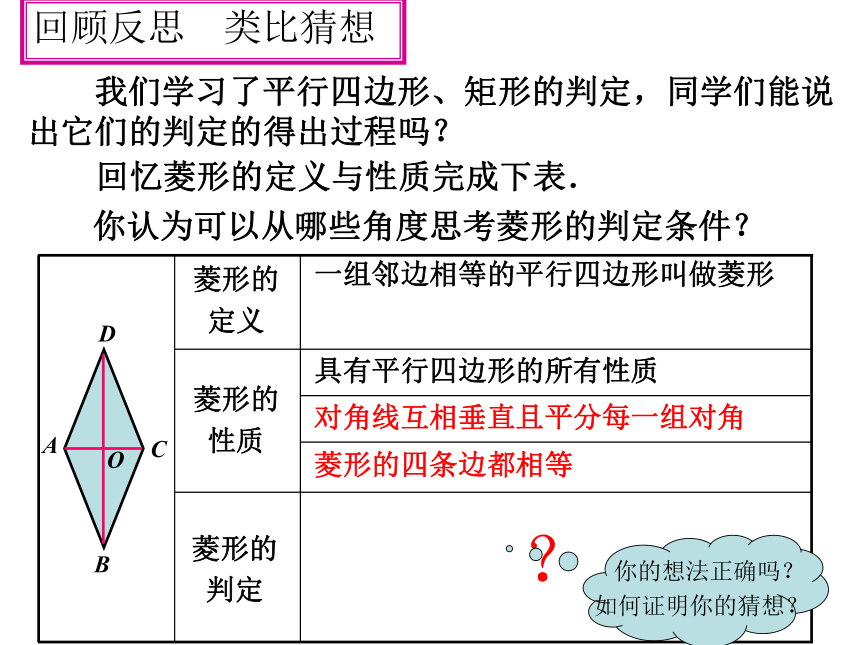
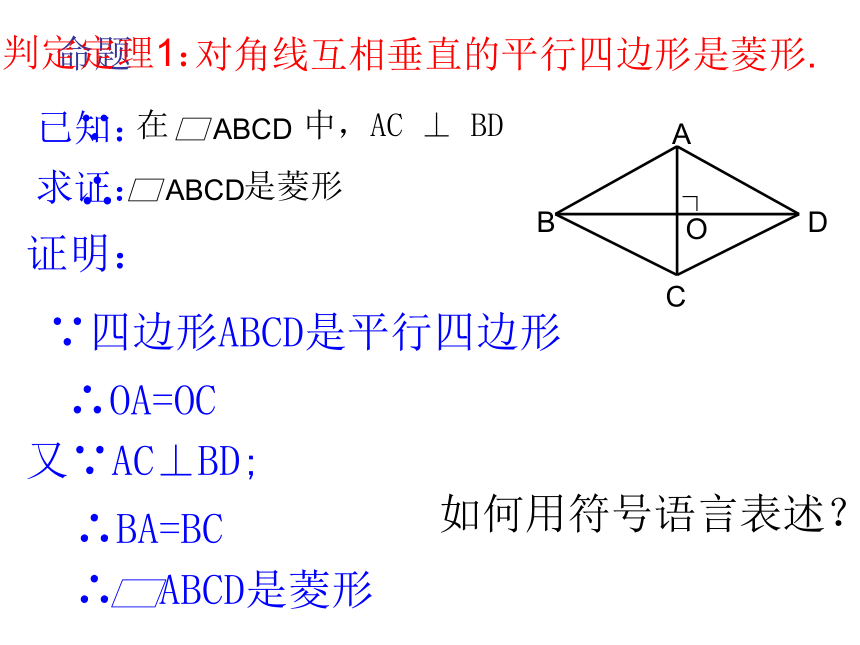
2.能根据不同的已知条件,选择适当的判定定理进行推理和计算.回顾反思 类比猜想 我们学习了平行四边形、矩形的判定,同学们能说出它们的判定的得出过程吗?一组邻边相等的平行四边形叫做菱形 具有平行四边形的所有性质对角线互相垂直且平分每一组对角 菱形的四条边都相等 ? 回忆菱形的定义与性质完成下表.你认为可以从哪些角度思考菱形的判定条件? 命题1:对角线互相垂直的平行四边形是菱形命题2:四条边都相等的四边形是菱形猜想:对角线互相垂直的平行四边形是菱形.证明:∵四边形ABCD是平行四边形∴OA=OC又∵AC⊥BD; ∴BA=BC 命题判定定理1:已知:求证:∵∴如何用符号语言表述?有四条边相等的四边形是菱形。命题判定定理2: 在四边形ABCD中,AB=BC=CD=DA.
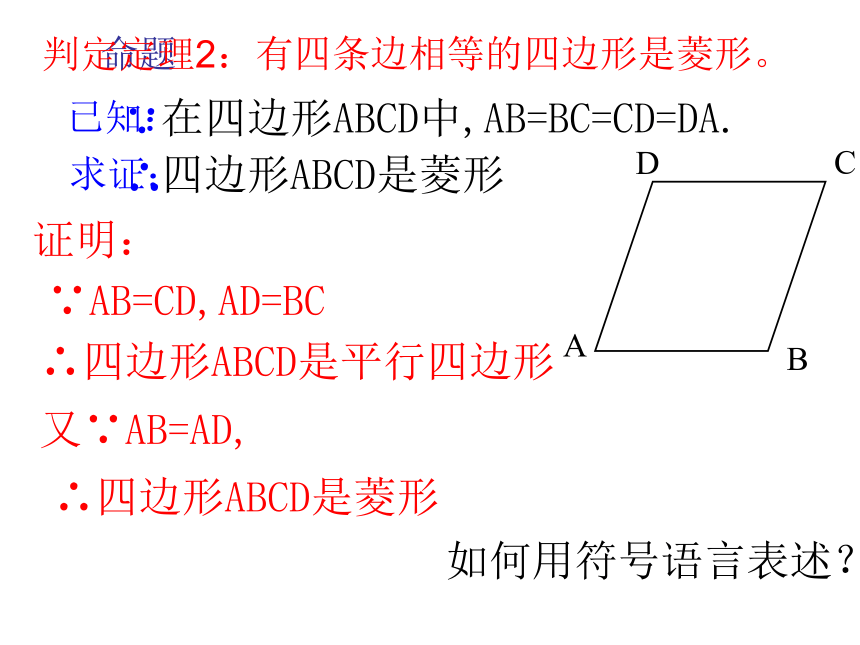
四边形ABCD是菱形证明:∵AB=CD,AD=BC∴四边形ABCD是平行四边形又∵AB=AD,∴四边形ABCD是菱形已知:求证:∵∴如何用符号语言表述?(1)定义:一组邻边相等的平行四边形叫做菱形。
(2)判定定理1:对角线互相垂直的平行四边形是菱形。
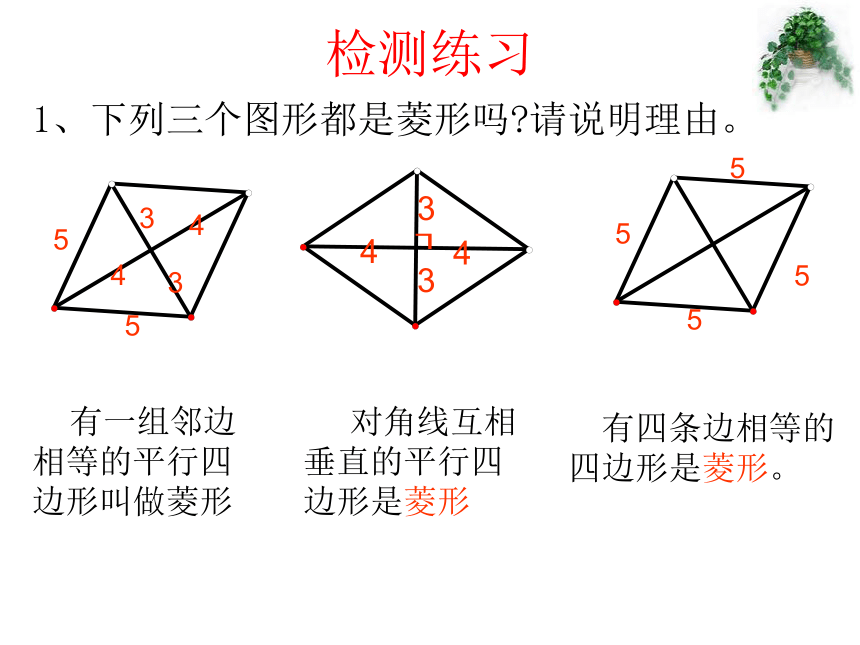
(3)判定定理2:四条边相等的四边形是菱形。菱形的判定方法1、下列三个图形都是菱形吗?请说明理由。 有一组邻边相等的平行四边形叫做菱形 对角线互相垂直的平行四边形是菱形 有四条边相等的四边形是菱形。检测练习四条边都相等菱形一组邻边相等对角线互相垂直5种方法方法总结四边形平行四边形(4)有一组邻边相等的四边形是菱形( ) 2、判断下列命题是否正确,并说明理由:(1)对角线互相平分且邻边相等的四边形
是菱形( )(2)两组对边分别平行且一组邻边相等
的四边形是菱形( )(3)邻角相等的四边形是菱形( )XX检测练习(5)对角线互相垂直的四边形是菱形( )X(6)对角线互相垂直平分的四边形是菱形( )3.下列条件中,不能判定四边形ABCD为菱形的是( ).
A、AC⊥BD ,AC与BD互相平分
B、AB=BC=CD=DA
C、AB=BC,AD=CD,且AC ⊥BD
D、AB=CD,AD=BC,AC ⊥BDBC检测练习解决问题我们怎样证明这个绿丝带重叠部分是一个菱形呢?已知:绿丝带是由一个宽度不变的矩形围成的。 已知:如图,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F.求证:四边形AEDF是菱形. 证明:∵DE∥AC,DF∥AB ∴四边形AEDF是平行四边形 ∴∠2=∠3又∵AD平分∠BAC ∴∠1=∠2
∴AE=ED(邻边相等的平行四边形是菱形) ∴四边形AEDF是菱形 巩固练习∴∠1=∠3一条对角线平分一个内角的平行四边形是菱形。 问题研讨:
如图, 在△ABC中, AB=AC, 点M在边BC上, 过点M分别作AB、AC的平行线, 与AC、AB分别相交于点D、E. 当点M位于BC的什么位置时, 四边形AEMD是菱形?请给予证明.当M为BC的中点时,四边形AEMD是菱形我们的收获:学 而 不 “悟 ” 则 罔回头一看,我想说…课堂反思对自己说,你有哪些收获?
知识方面、数学思想方法方面对同学说,你有哪些温馨提示?堂清测试题答案1、√ × √ × ×
2、C 3、C 4、AB=AD或AC⊥BD 5、是菱形
∵AO2+BO2=5
AB2=5
∴AO2+BO2=AB2
∴AC⊥BD
又∵四边形ABCD为平行四边形
∴ ABCD是菱形
6、是菱形
∵AB ∥CD
AB=CD
∴四边形ABCD为平行四边形
又∵AB=BC
∴ ABCD为菱形
2、已知:平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F。 求证:四边形AFCE是菱形。ABEDCFO12证明:平行四边形ABCD中AD∥BC∴∠1=∠2,∠3=∠443EF垂直平分AC∴AO=CO,AF=CF,AE=CE∴ △AOF≌△COE∴ AF=CE∴ AF=CF=AE=CE∴四边形AFCE是菱形四条边都相等的四边形是菱形巩固练习 2、已知:平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F。 求证:四边形AFCE是菱形。ABEDCFO12证明:平行四边形ABCD中AD∥BC∴∠1=∠2,∠3=∠443EF垂直平分AC∴AO=CO,AF=CF,∴ △AOF≌△COE∴ AF=CE∴平行四边形四边形AFCE是菱形又AF∥CE∴四边形AFCE是平行四边形一组邻边相等的平行四边形是菱形巩固练习 2、已知:平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F。 求证:四边形AFCE是菱形。ABEDCFO123’证明:平行四边形ABCD中AD∥BC∴∠1=∠2,∠3=∠443EF垂直平分AC∴AO=CO,AC⊥EF,∴ △AOF≌△COE∴ AF=CE∴平行四边形四边形AFCE是菱形又AF∥CE∴四边形AFCE是平行四边形对角线互相垂直的平行四边形是菱形巩固练习谢谢指导
菱形的判定学习目标:
1.探究并证明菱形判定定理,体会类比思想和转化的数学思想,了解研究图形判定的一般思路.
2.能根据不同的已知条件,选择适当的判定定理进行推理和计算.回顾反思 类比猜想 我们学习了平行四边形、矩形的判定,同学们能说出它们的判定的得出过程吗?一组邻边相等的平行四边形叫做菱形 具有平行四边形的所有性质对角线互相垂直且平分每一组对角 菱形的四条边都相等 ? 回忆菱形的定义与性质完成下表.你认为可以从哪些角度思考菱形的判定条件? 命题1:对角线互相垂直的平行四边形是菱形命题2:四条边都相等的四边形是菱形猜想:对角线互相垂直的平行四边形是菱形.证明:∵四边形ABCD是平行四边形∴OA=OC又∵AC⊥BD; ∴BA=BC 命题判定定理1:已知:求证:∵∴如何用符号语言表述?有四条边相等的四边形是菱形。命题判定定理2: 在四边形ABCD中,AB=BC=CD=DA.
四边形ABCD是菱形证明:∵AB=CD,AD=BC∴四边形ABCD是平行四边形又∵AB=AD,∴四边形ABCD是菱形已知:求证:∵∴如何用符号语言表述?(1)定义:一组邻边相等的平行四边形叫做菱形。
(2)判定定理1:对角线互相垂直的平行四边形是菱形。
(3)判定定理2:四条边相等的四边形是菱形。菱形的判定方法1、下列三个图形都是菱形吗?请说明理由。 有一组邻边相等的平行四边形叫做菱形 对角线互相垂直的平行四边形是菱形 有四条边相等的四边形是菱形。检测练习四条边都相等菱形一组邻边相等对角线互相垂直5种方法方法总结四边形平行四边形(4)有一组邻边相等的四边形是菱形( ) 2、判断下列命题是否正确,并说明理由:(1)对角线互相平分且邻边相等的四边形
是菱形( )(2)两组对边分别平行且一组邻边相等
的四边形是菱形( )(3)邻角相等的四边形是菱形( )XX检测练习(5)对角线互相垂直的四边形是菱形( )X(6)对角线互相垂直平分的四边形是菱形( )3.下列条件中,不能判定四边形ABCD为菱形的是( ).
A、AC⊥BD ,AC与BD互相平分
B、AB=BC=CD=DA
C、AB=BC,AD=CD,且AC ⊥BD
D、AB=CD,AD=BC,AC ⊥BDBC检测练习解决问题我们怎样证明这个绿丝带重叠部分是一个菱形呢?已知:绿丝带是由一个宽度不变的矩形围成的。 已知:如图,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F.求证:四边形AEDF是菱形. 证明:∵DE∥AC,DF∥AB ∴四边形AEDF是平行四边形 ∴∠2=∠3又∵AD平分∠BAC ∴∠1=∠2
∴AE=ED(邻边相等的平行四边形是菱形) ∴四边形AEDF是菱形 巩固练习∴∠1=∠3一条对角线平分一个内角的平行四边形是菱形。 问题研讨:
如图, 在△ABC中, AB=AC, 点M在边BC上, 过点M分别作AB、AC的平行线, 与AC、AB分别相交于点D、E. 当点M位于BC的什么位置时, 四边形AEMD是菱形?请给予证明.当M为BC的中点时,四边形AEMD是菱形我们的收获:学 而 不 “悟 ” 则 罔回头一看,我想说…课堂反思对自己说,你有哪些收获?
知识方面、数学思想方法方面对同学说,你有哪些温馨提示?堂清测试题答案1、√ × √ × ×
2、C 3、C 4、AB=AD或AC⊥BD 5、是菱形
∵AO2+BO2=5
AB2=5
∴AO2+BO2=AB2
∴AC⊥BD
又∵四边形ABCD为平行四边形
∴ ABCD是菱形
6、是菱形
∵AB ∥CD
AB=CD
∴四边形ABCD为平行四边形
又∵AB=BC
∴ ABCD为菱形
2、已知:平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F。 求证:四边形AFCE是菱形。ABEDCFO12证明:平行四边形ABCD中AD∥BC∴∠1=∠2,∠3=∠443EF垂直平分AC∴AO=CO,AF=CF,AE=CE∴ △AOF≌△COE∴ AF=CE∴ AF=CF=AE=CE∴四边形AFCE是菱形四条边都相等的四边形是菱形巩固练习 2、已知:平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F。 求证:四边形AFCE是菱形。ABEDCFO12证明:平行四边形ABCD中AD∥BC∴∠1=∠2,∠3=∠443EF垂直平分AC∴AO=CO,AF=CF,∴ △AOF≌△COE∴ AF=CE∴平行四边形四边形AFCE是菱形又AF∥CE∴四边形AFCE是平行四边形一组邻边相等的平行四边形是菱形巩固练习 2、已知:平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F。 求证:四边形AFCE是菱形。ABEDCFO123’证明:平行四边形ABCD中AD∥BC∴∠1=∠2,∠3=∠443EF垂直平分AC∴AO=CO,AC⊥EF,∴ △AOF≌△COE∴ AF=CE∴平行四边形四边形AFCE是菱形又AF∥CE∴四边形AFCE是平行四边形对角线互相垂直的平行四边形是菱形巩固练习谢谢指导
