5.1 轴对称现象同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
5.1 轴对称现象同步练习
　班级__________姓名____________总分___________
本节应掌握和应用的知识点
１． 如果一个图形沿一条直线折叠后,直线两旁的部分能够 互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴 ． www-2-1-cnjy-com
２．把一个图形沿着某一条直线对折,如果能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做这两个图形的对称轴 ．2-1-c-n-j-y
基础知识和能力拓展精练
一、选择题
1．在一些美术字中，有的汉字是轴对称图形,下面4个汉字中，可以看作是轴对称图形的是（ ）
（A）吉 （B）祥 （C）如 （D）意
2．下列“QQ”表情中，属于轴对称图形的是（ ）
( http: / / www.21cnjy.com )
3．已知两条互不平行的线段AB和A′B′ ( http: / / www.21cnjy.com )关于直线1对称，AB和A′B′所在的直线交于点P，下面四个结论：①AB=A′B′；②点P在直线1上；③若A、A′是对应点，则直线1垂直平分线段AA′；④若B、B′是对应点，则PB=PB′，其中正确的是（　　）
　 A． ①③④ B． ③④ C． ①② D． ①②③④
4．如图,关于虚线成轴对称的有(　　)个.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
A. 1 B. 2 C. 3 D. 4
5．下列说法中,正确的是(　　)
A. 关于某条直线对称的两个三角形是全等三角形
B. 全等的两个三角形是关于某条直线对称的
C. 两个图形关于某条直线对称,则这两个图形一定分别位于这条直线的两侧
D. 全等的两个图形一定成轴对称
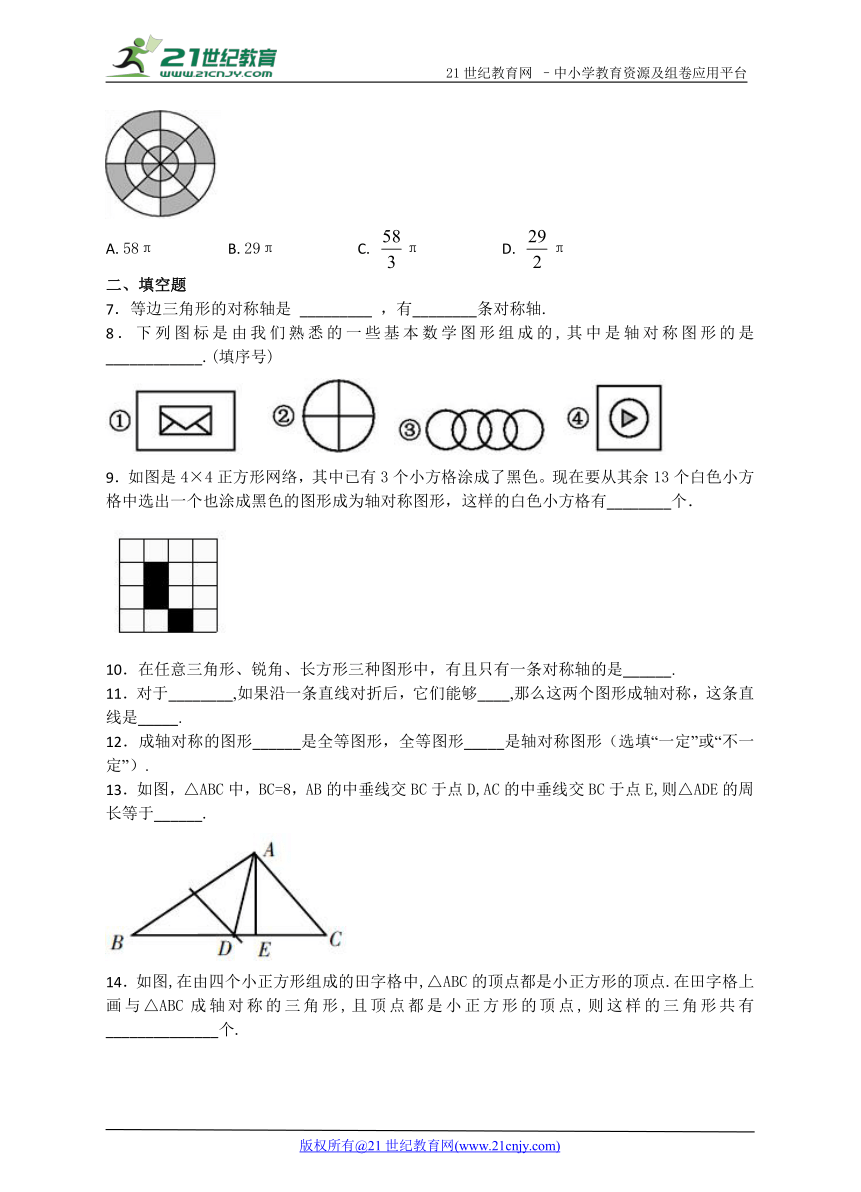
6．如图,最外面大圆的面积为58π,则阴影部分的面积为(　　)
( http: / / www.21cnjy.com )
A. 58π B. 29π C. EMBED Equation.DSMT4 π D. π
二、填空题
7．等边三角形的对称轴是 _________ ，有________条对称轴.
8．下列图标是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是____________.(填序号) 21cnjy.com
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
9．如图是4×4正方形网络，其中已有3个小 ( http: / / www.21cnjy.com )方格涂成了黑色。现在要从其余13个白色小方格中选出一个也涂成黑色的图形成为轴对称图形，这样的白色小方格有________个．
( http: / / www.21cnjy.com )
10．在任意三角形、锐角、长方形三种图形中，有且只有一条对称轴的是______.
11．对于________,如果沿一条直线对折后，它们能够____,那么这两个图形成轴对称，这条直线是_____.21*cnjy*com
12．成轴对称的图形______是全等图形，全等图形_____是轴对称图形（选填“一定”或“不一定”）.【来源：21cnj*y.co*m】
13．如图，△ABC中，BC=8，AB的中垂线交BC于点D,AC的中垂线交BC于点E,则△ADE的周长等于______.【出处：21教育名师】
( http: / / www.21cnjy.com )
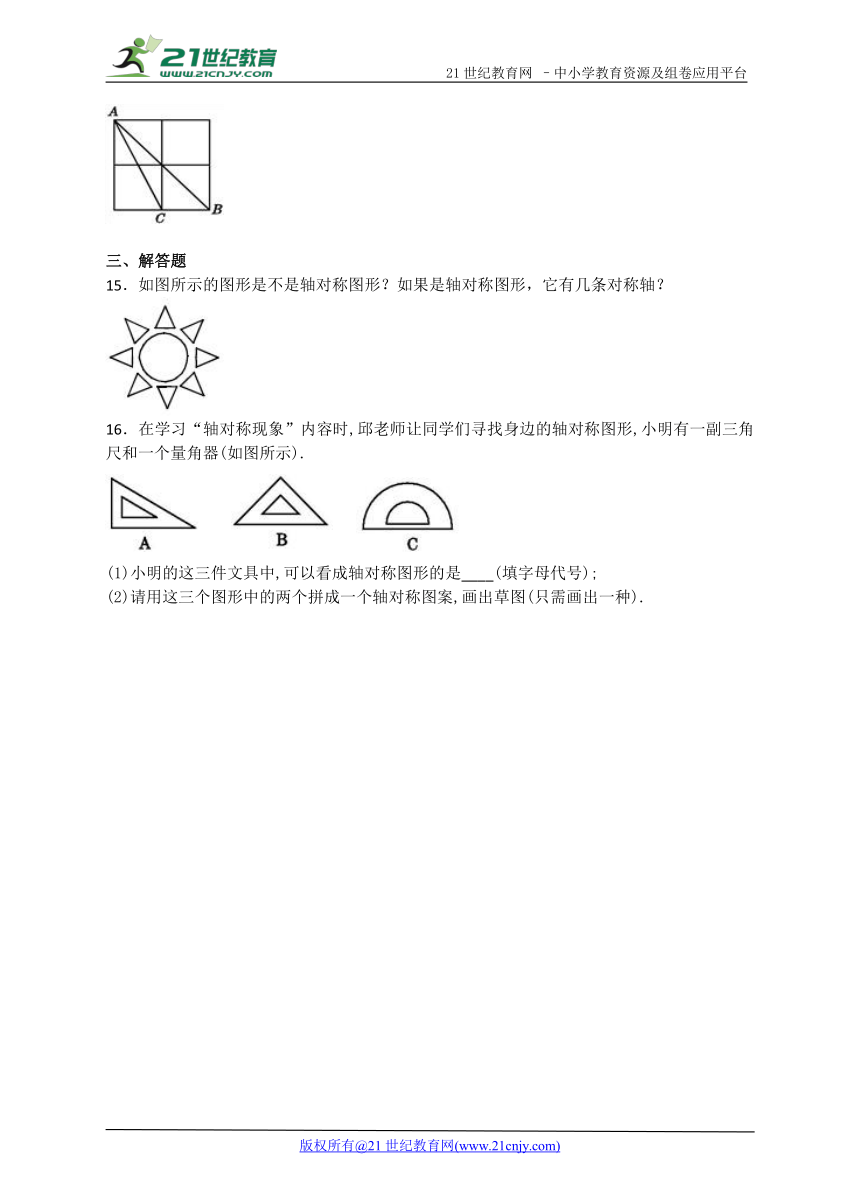
14．如图,在由四个小正方形组成的田字格中 ( http: / / www.21cnjy.com ),△ABC的顶点都是小正方形的顶点.在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形共有______________个. 【版权所有：21教育】
( http: / / www.21cnjy.com )
三、解答题
15．如图所示的图形是不是轴对称图形？如果是轴对称图形，它有几条对称轴？
( http: / / www.21cnjy.com )
16．在学习“轴对称现象”内容时,邱老师让同学们寻找身边的轴对称图形,小明有一副三角尺和一个量角器(如图所示).21教育名师原创作品
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1)小明的这三件文具中,可以看成轴对称图形的是____(填字母代号);
(2)请用这三个图形中的两个拼成一个轴对称图案,画出草图(只需画出一种).
参考答案
1．A．
【解析】
试题分析：根据轴对称图形的 ( http: / / www.21cnjy.com )概念，在一个平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形；四个选项中只有选项A符合要求，故答案选A．21世纪教育网版权所有
考点：轴对称图形的概念．
2．D
【解析】因为轴对称图形的概念是:将一个图形沿着某条直线翻折后,直线两侧的部分能够完全重合的图形是轴对称图形,故选D.21教育网
点睛:本题主要轴对称图形,解决本题的关键是要熟练掌握轴对称图形的概念.
3．D
【解析】
根据轴对称的性质，对应点的连线与对称轴 ( http: / / www.21cnjy.com )的位置关系是互相垂直，对应点所连的线段被对称轴垂直平分，对称轴上的任何一点到两个对应点之间的距离相等，对应的角、线段都相等．①②③④均正确
故选D．
4．B
【解析】①关于虚线不成轴对称，②关于虚线不成轴对称，③关于虚线不成轴对称，④关于虚线成轴对称，
故选B.
5．A
【解析】A. 关于某条直线对称的两个三角形是全等三角形，正确；
B. 全等的两个三角形不一定关于某条直线对称，如图一，
( http: / / www.21cnjy.com )
故B错误；
C. 两个图形关于某条直线对称,则这两个图形不一定分别位于这条直线的两侧，如图二，
( http: / / www.21cnjy.com )
故C错误；
D. 全等的两个图形不一定成轴对称，如B中的图一，故D错误，
故选A.
6．B
【解析】根据图形可以看出阴影部分的面积是总面积的一半，
阴影部分的面积=×58π=29π，
故选B．
【点睛】本题考查了轴对称的性质、圆的认识等，能够结合图形得出阴影部分的面积和大圆面积之间的关系是解题的关键.21·cn·jy·com
7． 每条边的中线所在直线 3
【解析】等边三角形有三条对称轴，对称轴是每条边的中线所在的直线，故答案为(1)每条边的中线所在直线，(2)3.www.21-cn-jy.com
8．①②③④
【解析】①是轴对称图形，②是轴对称图形，③是轴对称图形，④是轴对称图形，
故答案为：①②③④.
9．4
【解析】试题分析：根据轴对称图形的概念分别找出各个能成轴对称图形的小方格即可．如图所示，有4个位置使之成为轴对称图形．2·1·c·n·j·y
故答案为：4．
( http: / / www.21cnjy.com )
考点：利用轴对称设计图案．
10．锐角
【解析】因为任意一个三角形有可能不 ( http: / / www.21cnjy.com )是轴对称图形,也有可能是轴对称图形,所以对称轴的个数不确定,所以不符合题意,因为锐角是关于角平分线所在直线对称,所以对称轴有且只有一条,因为长方形的对称轴有两条,不符合题意,故答案为:锐角.【来源：21·世纪·教育·网】
11． 两个图形 完全重合 对称轴
【解析】因为成轴对称的概念是:将两 ( http: / / www.21cnjy.com )个图形沿着某条直线翻折后,他们能够完全重合,那么这两个图形成轴对称,这条直线是对称轴,故答案为:两个图形,完全重合,对称轴.
12． 一定 不一定
【解析】根据轴对称的概念可知:成轴对称的两个 ( http: / / www.21cnjy.com )图形是全等图形,但全等图形不一定成轴对称,由于两个图形摆放的位置，不一定能使得沿一条直线翻折后两个图形重合.
13．4cm
【解析】因为AB的中垂线交BC于D，AC的中垂线交BC与E，所以AD=DB，AE=CE.
△ADE的周长为AD+DE+AE=BD+DE+EC=BC=8.
故答案为8.
14．3
【解析】如图所示：符合题意的有3个三角形，
故答案为：3.
( http: / / www.21cnjy.com )
【点睛】本题主要考查了利用轴对称设计图案，正确把握轴对称图形的性质是解题关键．
15．是轴对称图形，有4条对称轴
【解析】试题分析:根据轴对称图形的概念进行识别,根据对称轴的概念进行求解.
试题解析:因为将图形沿着某条直线翻折后,直线两侧的部分能够完全重合,所以是轴对称图形,它的对称轴有4条.21·世纪*教育网
16．（1）B、C；（2）画图见解析.
【解析】试题分析：(1)根据轴对称图形的概念进行判断即可得；
(2)根据轴对称图形的概念选择轴对称图形进行拼图即可得.
试题解析：(1)小明的这三件文具中，可以看做是轴对称图形的是B、C，
故答案为：B、C；
(2)如图所示：
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)