北师大八年级下《第三章图形的平移与旋转》单元测试(含答案)
文档属性
| 名称 | 北师大八年级下《第三章图形的平移与旋转》单元测试(含答案) | 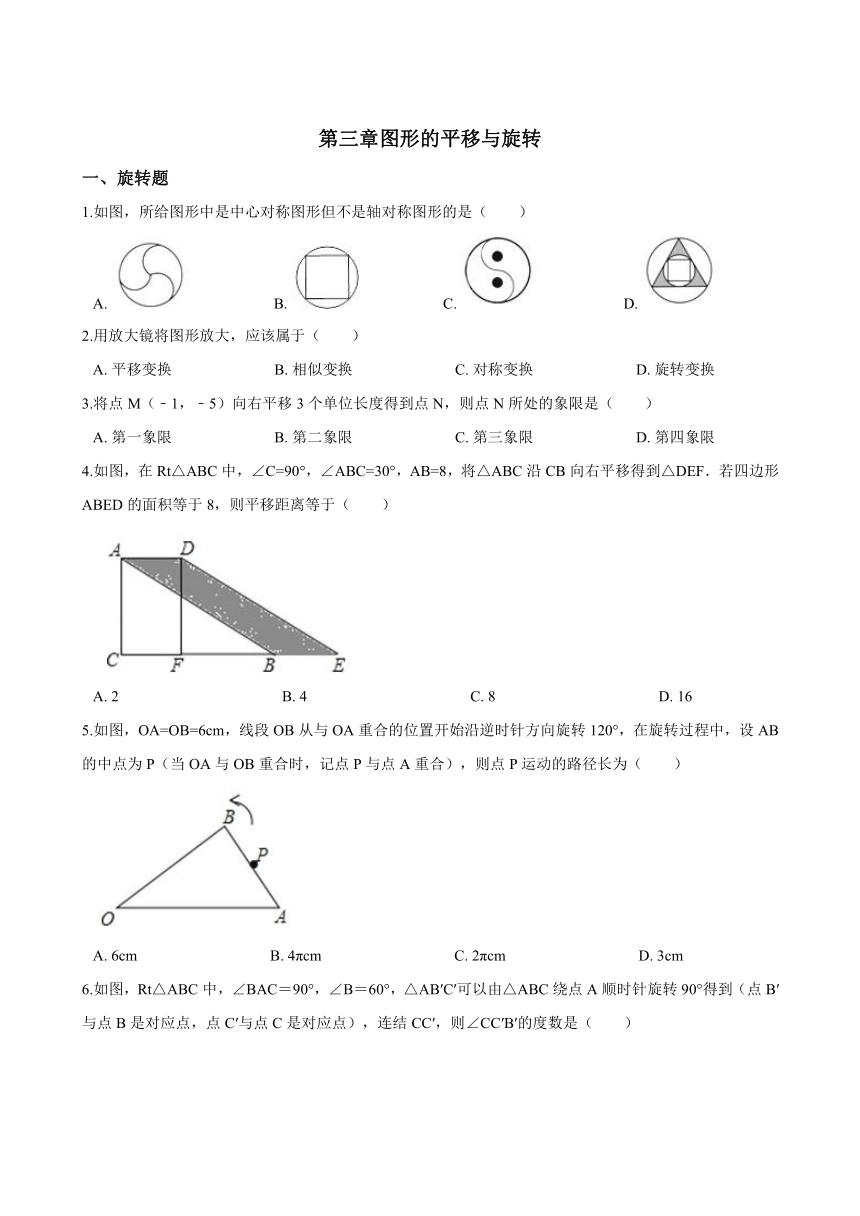 | |
| 格式 | zip | ||
| 文件大小 | 342.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-04 20:10:07 | ||
图片预览


文档简介
第三章图形的平移与旋转
一、旋转题
1.如图,所给图形中是中心对称图形但不是轴对称图形的是( )
A.???????????????????????B.???????????????????????C.???????????????????????D.?
2.用放大镜将图形放大,应该属于( )
A.?平移变换???????????????????????????B.?相似变换???????????????????????????C.?对称变换???????????????????????????D.?旋转变换
3.将点M(﹣1,﹣5)向右平移3个单位长度得到点N,则点N所处的象限是( )
A.?第一象限???????????????????????????B.?第二象限???????????????????????????C.?第三象限???????????????????????????D.?第四象限
4.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=8,将△ABC沿CB向右平移得到△DEF.若四边形ABED的面积等于8,则平移距离等于( )
A.?2???????????????????????????????????????????B.?4???????????????????????????????????????????C.?8???????????????????????????????????????????D.?16
5.如图,OA=OB=6cm,线段OB从与OA重合的位置开始沿逆时针方向旋转120°,在旋转过程中,设AB的中点为P(当OA与OB重合时,记点P与点A重合),则点P运动的路径长为( )
A.?6cm???????????????????????????????????B.?4πcm???????????????????????????????????C.?2πcm???????????????????????????????????D.?3cm
6.如图,Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连结CC′,则∠CC′B′的度数是( )
A.?45°???????????????????????????????????????B.?30°???????????????????????????????????????C.?25°???????????????????????????????????????D.?15°
7.如图,等腰直角三角形ABC的直角边AB的长为6cm,将△ABC绕点A逆时针旋转15°后得到△AB′C′,AC与B′C′相交于点H,则图中△AHC′的面积等于( )
A.?12﹣6????????????????????????????B.?14﹣6???????????????????????????C.?18﹣6???????????????????????????D.?18+6
8.如图所示是“福娃欢欢”的五幅图案,②,③,④,⑤哪一个图案可以通过平移图案①得到( )
A.?②?????????????????????????????????????????B.?③?????????????????????????????????????????C.?④?????????????????????????????????????????D.?⑤
9.如图,在正方形ABCD中,AB=3,点E在CD边上,DE=1,把△ADE绕点A顺时针旋转90°,得到△ABE′,连接EE′,则线段EE′的长为( )
A.???????????????????????????????????????B.???????????????????????????????????????C.?4??????????????????????????????????????D.?
10.如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,△ABD经旋转后到达△ACE的位置,那么旋转了(??????? ).
A.?75°???????????????????????????????????????B.?60°???????????????????????????????????????C.?45°???????????????????????????????????????D.?15°
二、填空题
11.在等边三角形、正方形、直角三角形、等腰梯形中,既是轴对称图形,又是中心对称图形的是?________ .
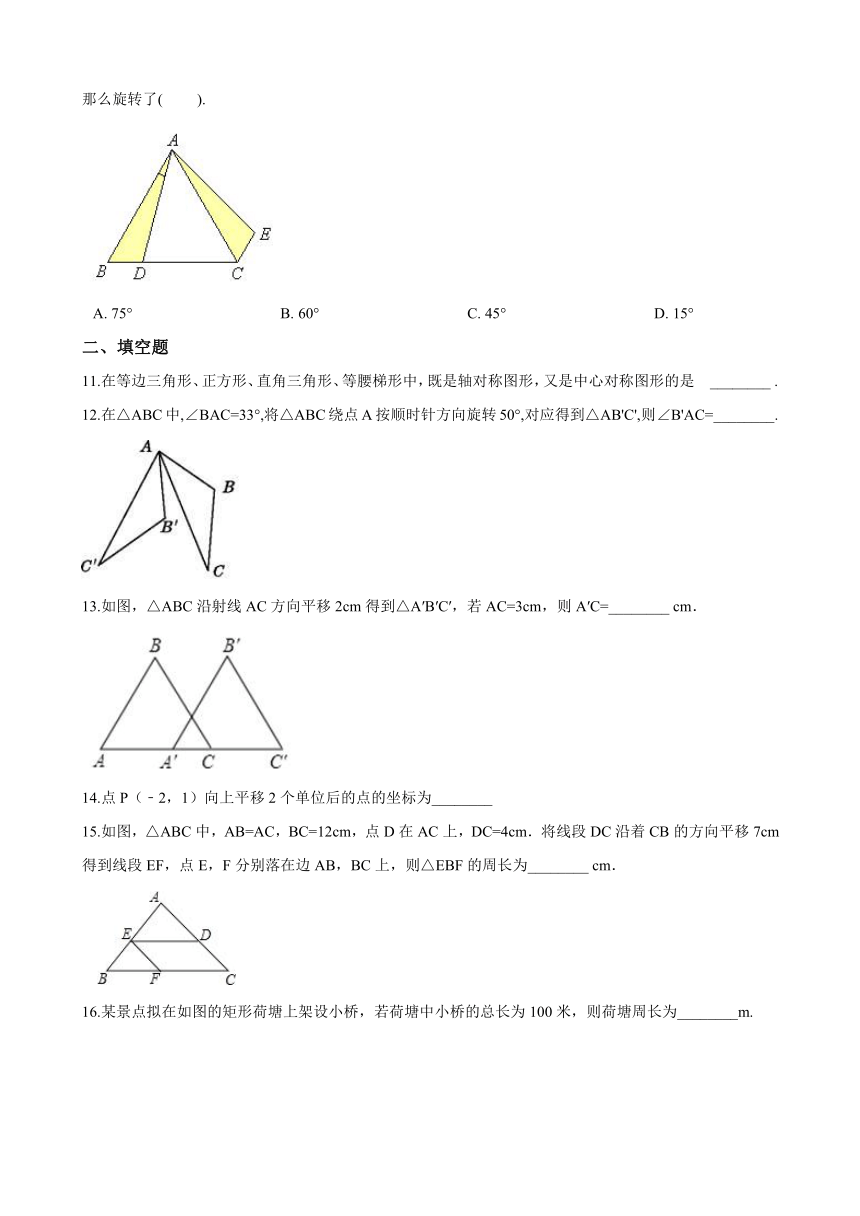
12.在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB'C',则∠B'AC=________.
13.如图,△ABC沿射线AC方向平移2cm得到△A′B′C′,若AC=3cm,则A′C=________?cm.
14.点P(﹣2,1)向上平移2个单位后的点的坐标为________?
15.如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm.将线段DC沿着CB的方向平移7cm得到线段EF,点E,F分别落在边AB,BC上,则△EBF的周长为________?cm.
16.某景点拟在如图的矩形荷塘上架设小桥,若荷塘中小桥的总长为100米,则荷塘周长为________m.
三、解答题
17.如图所示,有一条宽相等的小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,若要硬化这条小路,且每平方米造价50元,则需要多少元钱?
18.请把下面的小船图案先向上平移3格,再向右平移4格,最后为这个图案配上一句简短的解说词.
19.每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上, ①把△ABC向上平移5个单位后得到对应的△A1B1C1 , 画出△A1B1C1 , ②以原点O为对称中心,再画出与△A1B1C1关于原点O对称的△A2B2C2 .
参考答案
一、旋转题
C B D A C D C D A B
二、填空题
11. 正方形
12. 17°
13. 1
14. (﹣2,3)
15. 13
16. 200
三、解答题
17. 解:在矩形ABCD中,AF∥EC, 又∵AF=EC, ∴四边形AECF是平行四边形. 在Rt△ABE中,AB=60,AE=100, 根据勾股定理得BE=80, ∴EC=BC﹣BE=4, 所以这条小路的面积S=EC?AB=4×60=240(m2). 240×50=1200元. 答:需要1200元钱
18. 解:如图所示:
解说词:两只小船在水中向前滑行
19. 解:如图所示:
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
